【pytorch学习实战】第五篇:卷积神经网络实现MNIST手写数字识别
往期相关文章列表:
- 【pytorch学习实战】第一篇:线性回归
- 【pytorch学习实战】第二篇:多项式回归
- 【pytorch学习实战】第三篇:逻辑回归
- 【pytorch学习实战】第四篇:MNIST数据集的读取、显示以及全连接实现数字识别
- 【pytorch学习实战】第五篇:卷积神经网络实现MNIST手写数字识别
- 【pytorch实战学习】第六篇:CIFAR-10分类实现
- 【pytorch实战学习】第七篇:tensorboard可视化介绍
我们在这里尽可能的讲解一些实战编程方面的内容,所以我们会尽可能避免过多地介绍基础理论知识,如果想要深入了解卷积神经网络CNN,可以访问本人之前写过的一篇文章。
1. 前言介绍
我们这里使用的CNN包括了卷积层和池化层,下面我们对它们进行简要介绍。
- 卷积层:nn.Conv2d()
这是一个2d卷积操作,它的原型如下:
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1,
bias=True, padding_mode='zeros', device=None, dtype=None)
如果想要详细了解nn.Conv2d(),可点击官网链接进行查阅。
| 参数 | 含义 |
|---|---|
| in_channels | 输入信号的通道数. |
| out_channels | 卷积后输出结果的通道数. |
| kernel_size | 卷积核的大小. 例如kernel_size=(3, 2)表示3X2的卷积核,如果宽和高相同,可以只用一个数字表示 |
| stride | 卷积每次移动的步长, 默认为1. |
| padding | 处理边界时填充0的数量, 默认为0(不填充). |
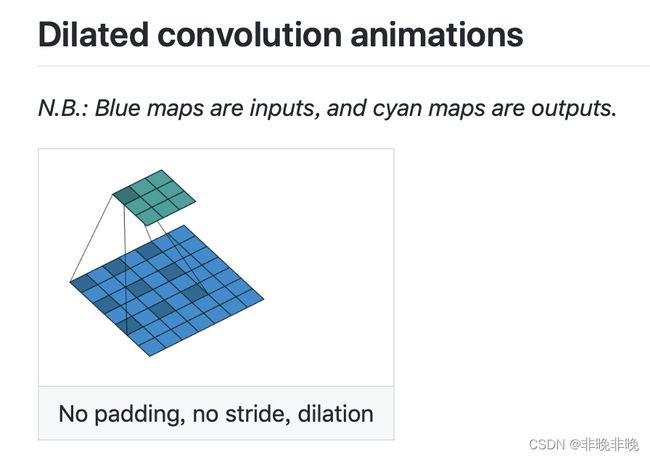
| dilation | 扩展系数,也就是采样间隔数, 默认为1, 无间隔采样。dilation的效果如下。 |
| groups | 输入与输出通道的分组数量。groups个共用一组weight。默认值为1, 对应的是常规卷积操作。group=in_channels时,每一个输入通道和它对应的卷积核进行卷积,对应的卷积核大小为 C o u t / C i n C_{out}/C_{in} Cout/Cin |
| bias | 为 True 时, 添加偏置。 |
| padding_mode | ‘zeros’, ‘reflect’, ‘replicate’ or ‘circular’. Default: ‘zeros’ |
- 池化层:nn.MaxPool2d()
我们这里使用的是一个2d的最大池化操作,它的原型如下:
torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
如果想要详细了解nn.MaxPool2d(),可点击官网链接进行查阅。
| 参数 | 含义 |
|---|---|
| kernel_size | 最大池化操作时的窗口大小 |
| stride | 最大池化操作时窗口移动的步长, 默认值是0 |
| padding | 输入的每条边隐式补0的数量 |
| dilation | 扩展系数,用于控制窗口中元素的步长的参数 |
| return_indices | 如果等于 True, 在返回 max pooling 结果的同时返回最大值的索引,这对torch.nn.MaxUnpool2d 时很有用 |
| ceil_mode | 如果等于 True, 在计算输出大小时,将采用向上取整来代替默认的向下取整的方式,默认向下取整。 |
2. CNN实现手写识别
使用CNN实现手写识别中,我们一共定义了五层,其中两层卷积层,两层池化层,最后一层为FC层进行分类输出。其网络结构如下:
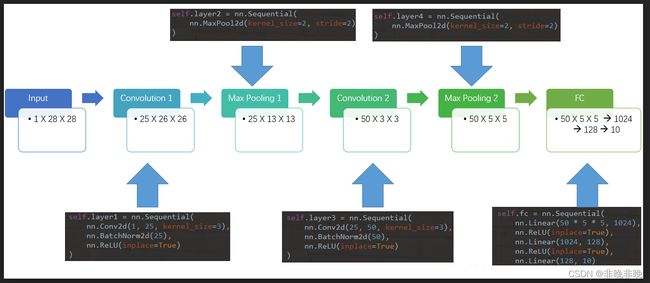
代码如下:
from torch import nn
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__()
self.layer1 = nn.Sequential(
nn.Conv2d(1, 25, kernel_size=3),
nn.BatchNorm2d(25),
nn.ReLU(inplace=True)
)
self.layer2 = nn.Sequential(
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.layer3 = nn.Sequential(
nn.Conv2d(25, 50, kernel_size=3),
nn.BatchNorm2d(50),
nn.ReLU(inplace=True)
)
self.layer4 = nn.Sequential(
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.fc = nn.Sequential(
nn.Linear(50 * 5 * 5, 1024),
nn.ReLU(inplace=True),
nn.Linear(1024, 128),
nn.ReLU(inplace=True),
nn.Linear(128, 10)
)
def forward(self, x):
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
x = self.layer4(x)
x = x.view(x.size(0), -1)
x = self.fc(x)
return x
import torch
from torch import nn, optim
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
#-------------------------------------超参数定义-------------------------------------
batch_size = 64 #一个batch的size
learning_rate = 0.02
num_epoches = 3 #总样本的迭代次数
#-------------------------------------数据预处理方法--------------------------------------
# transforms.ToTensor()将图片转换成PyTorch中处理的对象Tensor,并且进行标准化(数据在0~1之间)
# transforms.Normalize()做归一化。它进行了减均值,再除以标准差。两个参数分别是均值和标准差
# transforms.Compose()函数则是将各种预处理的操作组合到了一起
data_tf = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize([0.5], [0.5])])
#-------------------------------------数据集的下载器--------------------------------------
#训练和测试集预处理
train_dataset = datasets.MNIST(root='./data', train=True, transform=data_tf, download=True)
test_dataset = datasets.MNIST(root='./data', train=False, transform=data_tf)
#加载数据集
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
#-------------------------------------选择模型--------------------------------------
'''
1. 输入28*28(因为输入的图像像素为28*28)
2. 隐藏层分别为300和100
3. 输出层为10,因为识别的数字为0~9
'''
#下列3个模型可以任选其中之一
model = CNN()
# model = net.Activation_Net(28 * 28, 300, 100, 10)
# model = net.Batch_Net(28 * 28, 300, 100, 10)
if torch.cuda.is_available():
model = model.cuda()
#-------------------------------------定义损失函数和优化器--------------------------------------
#交叉熵和SGD优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
#-------------------------------------开始训练-------------------------------------
print('Start Training!')
iter = 0 #迭代次数
for epoch in range(num_epoches):
for data in train_loader:
img, label = data
#img = img.view(img.size(0), -1)
if torch.cuda.is_available():
img = img.cuda()
label = label.cuda()
else:
img = img
label = label
out = model(img)
loss = criterion(out, label)
optimizer.zero_grad()
loss.backward()
optimizer.step()
iter+=1
#每迭代50次打印一次
if iter%50 == 0:
print('epoch: {}, iter:{}, loss: {:.4}'.format(epoch, iter, loss.data.item()))
#-------------------------------------模型评估-------------------------------------
print('Start eval!')
model.eval()
eval_loss = 0
eval_acc = 0
for data in test_loader:
img, label = data
#img = img.view(img.size(0), -1)
if torch.cuda.is_available():
img = img.cuda()
label = label.cuda()
out = model(img)
loss = criterion(out, label)
eval_loss += loss.data.item()*label.size(0)
_, pred = torch.max(out, 1)
num_correct = (pred == label).sum()
eval_acc += num_correct.item()
print('Test Loss: {:.6f}, Acc: {:.6f}'.format(eval_loss / (len(test_dataset)), eval_acc / (len(test_dataset))))
输出状态如下所示,相比于上一篇文章,可以看到CNN比全连接实现手写识别的准确率有显著提高!
Start Training!
epoch: 0, iter:50, loss: 1.406
epoch: 0, iter:100, loss: 0.6279
epoch: 0, iter:150, loss: 0.2394
epoch: 0, iter:200, loss: 0.3516
epoch: 0, iter:250, loss: 0.2057
epoch: 0, iter:300, loss: 0.1028
epoch: 0, iter:350, loss: 0.1329
epoch: 0, iter:400, loss: 0.3032
epoch: 0, iter:450, loss: 0.1455
epoch: 0, iter:500, loss: 0.06673
epoch: 0, iter:550, loss: 0.1367
epoch: 0, iter:600, loss: 0.11
epoch: 0, iter:650, loss: 0.06825
epoch: 0, iter:700, loss: 0.1088
epoch: 0, iter:750, loss: 0.133
epoch: 0, iter:800, loss: 0.03325
epoch: 0, iter:850, loss: 0.1624
epoch: 0, iter:900, loss: 0.09274
epoch: 1, iter:950, loss: 0.05196
epoch: 1, iter:1000, loss: 0.02687
epoch: 1, iter:1050, loss: 0.0205
epoch: 1, iter:1100, loss: 0.02812
epoch: 1, iter:1150, loss: 0.1036
epoch: 1, iter:1200, loss: 0.02953
epoch: 1, iter:1250, loss: 0.04452
epoch: 1, iter:1300, loss: 0.02557
epoch: 1, iter:1350, loss: 0.07545
epoch: 1, iter:1400, loss: 0.07711
epoch: 1, iter:1450, loss: 0.04847
epoch: 1, iter:1500, loss: 0.06299
epoch: 1, iter:1550, loss: 0.04377
epoch: 1, iter:1600, loss: 0.06978
epoch: 1, iter:1650, loss: 0.03047
epoch: 1, iter:1700, loss: 0.0155
epoch: 1, iter:1750, loss: 0.04408
epoch: 1, iter:1800, loss: 0.0533
epoch: 1, iter:1850, loss: 0.0174
epoch: 2, iter:1900, loss: 0.09199
epoch: 2, iter:1950, loss: 0.03037
epoch: 2, iter:2000, loss: 0.05398
epoch: 2, iter:2050, loss: 0.1428
epoch: 2, iter:2100, loss: 0.02138
epoch: 2, iter:2150, loss: 0.03927
epoch: 2, iter:2200, loss: 0.03975
epoch: 2, iter:2250, loss: 0.03523
epoch: 2, iter:2300, loss: 0.1384
epoch: 2, iter:2350, loss: 0.09984
epoch: 2, iter:2400, loss: 0.06633
epoch: 2, iter:2450, loss: 0.08727
epoch: 2, iter:2500, loss: 0.02918
epoch: 2, iter:2550, loss: 0.1094
epoch: 2, iter:2600, loss: 0.01501
epoch: 2, iter:2650, loss: 0.03435
epoch: 2, iter:2700, loss: 0.02399
epoch: 2, iter:2750, loss: 0.05763
epoch: 2, iter:2800, loss: 0.03168
Start eval!
Test Loss: 0.042022, Acc: 0.986300