机器学习算法系列(十六)-非线性支持向量机算法(Non-Linear Support Vector Machine)
阅读本文需要的背景知识点:线性支持向量机、一丢丢编程知识
一、引言
前面我们用两节介绍了两种支持向量机模型——硬间隔支持向量机、软间隔支持向量机,这两种模型可以统称为线性支持向量机,下面来介绍另一种支持向量机模型——非线性支持向量机1 (Non-Linear Support Vector Machine)。
二、模型介绍
在介绍非线性支持向量机之前,让我们来看如下的线性不可分的数据集:
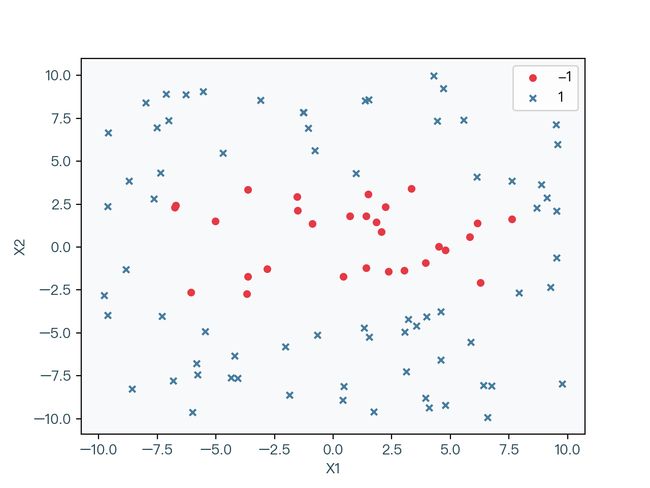
图 2-1 中分别用圆和叉来代表不同的标签分类,很明显该数据集无法通过一条直线正确分类,但是如图 2-2 所示,该数据集可以被一条椭圆曲线正确的分类。
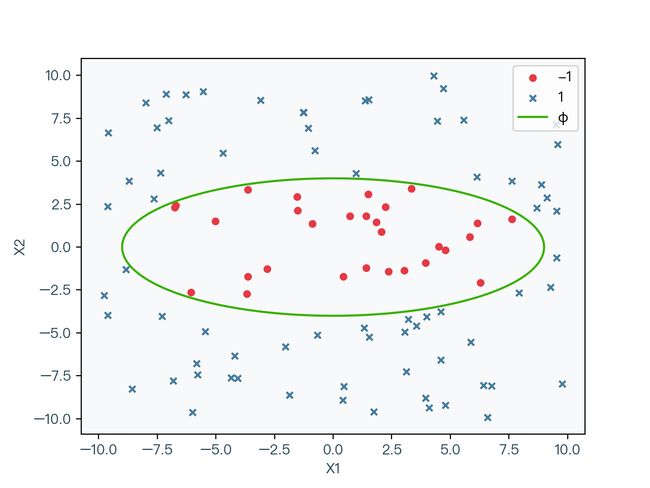
但是想要求解如图 2-2 中的椭圆曲线这种非线性分类的问题,相对来说难度较大。既然线性分类问题相对容易求解,那么该数据能否通过一定的非线性变化转化为一个线性分类的数据呢,答案是可以的。

如图 2-3 所示,将数据集进行非线性转换( Z = X ∗ X Z = X * X Z=X∗X),这时可以看到转换后的数据可以通过一条直线正确分类,原来图 2-2 中的椭圆曲线变换成了图 2-3 中的直线,原来非线性分类问题变换成了线性分类问题。
原始模型
先来回顾一下前面软间隔支持向量机的原始模型:
min w , b , ξ 1 2 w T w + C ∑ i = 1 N ξ i s.t. C > 0 ξ i ≥ 0 ξ i ≥ 1 − y i ( w T x i + b ) i = 1 , 2 , ⋯ , N \begin{array}{c} \underset{w, b, \xi}{\min} \frac{1}{2} w^{T} w+C \sum_{i=1}^{N} \xi_{i} \\ \text { s.t. } \quad C>0 \quad \xi_{i} \geq 0 \quad \xi_{i} \geq 1-y_{i}\left(w^{T} x_{i}+b\right) \quad i=1,2, \cdots, N \end{array} w,b,ξmin21wTw+C∑i=1Nξi s.t. C>0ξi≥0ξi≥1−yi(wTxi+b)i=1,2,⋯,N
假设存在一个 ϕ \phi ϕ 函数能对 x x x 进行变换,例如上面例子中的将 x x x 映射成 z z z,带入上面的软间隔支持向量机的原始模型中得:
min w , b , ξ 1 2 w T w + C ∑ i = 1 N ξ i s.t. C > 0 ξ i ≥ 0 ξ i ≥ 1 − y i ( w T ϕ ( x i ) + b ) i = 1 , 2 , ⋯ , N \begin{array}{c} \underset{w, b, \xi}{\min} \frac{1}{2} w^{T} w+C \sum_{i=1}^{N} \xi_{i} \\ \text { s.t. } \quad C>0 \quad \xi_{i} \geq 0 \quad \xi_{i} \geq 1-y_{i}\left(w^{T} \phi(x_{i})+b\right) \quad i=1,2, \cdots, N \end{array} w,b,ξmin21wTw+C∑i=1Nξi s.t. C>0ξi≥0ξi≥1−yi(wTϕ(xi)+b)i=1,2,⋯,N
上式 2-2 就是非线性支持向量机的原始模型。
对偶模型
同前面两节中所求解的对偶模型,可以得到非线性支持向量机的对偶模型:
max λ ∑ i = 1 N λ i − 1 2 ∑ i = 1 N ∑ j = 1 N λ i λ j y i y j ϕ ( x i ) T ϕ ( x j ) s.t. ∑ i = 1 N λ i y i = 0 0 ≤ λ i ≤ C i = 1 , 2 , ⋯ , N \begin{array}{c} \underset{\lambda}{\max} \sum_{i=1}^{N} \lambda_{i}-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \lambda_{i} \lambda_{j} y_{i} y_{j} \phi(x_{i})^{T} \phi(x_{j}) \\ \text { s.t. } \quad \sum_{i=1}^{N} \lambda_{i} y_{i}=0 \quad 0 \leq \lambda_{i} \leq C \quad i=1,2, \cdots, N \end{array} λmax∑i=1Nλi−21∑i=1N∑j=1Nλiλjyiyjϕ(xi)Tϕ(xj) s.t. ∑i=1Nλiyi=00≤λi≤Ci=1,2,⋯,N
核技巧
观察式 2-3 中对软间隔支持向量机的对偶模型的变化部分,特征向量经过 ϕ \phi ϕ 函数变换后,其维度数可能会很高,再求内积通常比较困难。为了绕过这个内积计算,我们可以找到一个如式 2-4 所示的函数,使得经过该函数计算后的值等于特征转换后的内积,这样的函数被称为核函数(Kernel Function),这种替换的方法被称为核技巧2(Kernel Trick)
K ( x i , x j ) = ϕ ( x i ) T ϕ ( x j ) K(x_i, x_j) = \phi(x_i)^T\phi(x_j) K(xi,xj)=ϕ(xi)Tϕ(xj)
使用核技巧带入式 2-3 后得到最终的非线性支持向量机的对偶模型:
max λ ∑ i = 1 N λ i − 1 2 ∑ i = 1 N ∑ j = 1 N λ i λ j y i y j K ( x i , x j ) s.t. ∑ i = 1 N λ i y i = 0 0 ≤ λ i ≤ C i = 1 , 2 , ⋯ , N \begin{array}{c} \underset{\lambda}{\max} \sum_{i=1}^{N} \lambda_{i}-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \lambda_{i} \lambda_{j} y_{i} y_{j} K(x_i, x_j) \\ \text { s.t. } \quad \sum_{i=1}^{N} \lambda_{i} y_{i}=0 \quad 0 \leq \lambda_{i} \leq C \quad i=1,2, \cdots, N \end{array} λmax∑i=1Nλi−21∑i=1N∑j=1NλiλjyiyjK(xi,xj) s.t. ∑i=1Nλiyi=00≤λi≤Ci=1,2,⋯,N
核技巧下的决策面:
(1)原始的决策面函数
(2)带入权重系数 w w w
(3)使用核技巧替换后得到最后的决策面函数
f ( x ) = w T ϕ ( x ) + b ( 1 ) = ∑ i = 1 N λ i y i ϕ ( x i ) ϕ ( x ) + b ( 2 ) = ∑ i = 1 N λ i y i K ( x i , x ) + b ( 3 ) \begin{aligned} f(x) &=w^{T} \phi(x)+b & (1)\\ &=\sum_{i=1}^{N} \lambda_{i} y_{i} \phi\left(x_{i}\right) \phi(x)+b & (2)\\ &=\sum_{i=1}^{N} \lambda_{i} y_{i} K\left(x_{i}, x\right)+b & (3) \end{aligned} f(x)=wTϕ(x)+b=i=1∑Nλiyiϕ(xi)ϕ(x)+b=i=1∑NλiyiK(xi,x)+b(1)(2)(3)
核技巧不仅仅适用于支持向量机,在其他机器学习算法中也有广泛的应用。
核函数
常用核函数:
(1)线性核函数(Linear Kernel):使用线性核函数的支持向量机分类结果与软间隔支持向量机的结果相同
(2)多项式核函数(Polynomial Kernel):当 γ = 1 , ε = 0 , d = 1 γ = 1,ε = 0,d = 1 γ=1,ε=0,d=1 时,多项式核函数退化为线性核函数
(3)径向基核函数(Radial basis function/RBF Kernel):常见的高斯核函数(Gaussian Kernel)是径向基核函数的一种
(4)Sigmoid核函数(Sigmoid Kernel): t a n h tanh tanh 为双曲正切函数
K ( x i , x j ) = x i T x j ( 1 ) K ( x i , x j ) = ( γ x i T x j + ε ) d ( 2 ) K ( x i , x j ) = e − γ ∥ x i − x j ∥ 2 ( 3 ) K ( x i , x j ) = tanh ( γ x i T x j + ε ) ( 4 ) \begin{aligned} K\left(x_{i}, x_{j}\right)&=x_{i}^{T} x_{j} & (1) \\ K\left(x_{i}, x_{j}\right)&=\left(\gamma x_{i}^{T} x_{j}+\varepsilon\right)^{d} & (2)\\ K\left(x_{i}, x_{j}\right)&=e^{-\gamma\left\|x_{i}-x_{j}\right\|^{2}} & (3)\\ K\left(x_{i}, x_{j}\right)&=\tanh \left(\gamma x_{i}^{T} x_{j}+\varepsilon\right) & (4) \end{aligned} K(xi,xj)K(xi,xj)K(xi,xj)K(xi,xj)=xiTxj=(γxiTxj+ε)d=e−γ∥xi−xj∥2=tanh(γxiTxj+ε)(1)(2)(3)(4)
三、算法步骤
对比软间隔支持向量机的对偶模型,非线性支持向量机只有特征向量的内积使用核函数替换,其他没有变化,所以对应的序列最小优化算法(SMO)变化也不大。
算法步骤请参考前面两节中的内容和下面的代码实现,同时可以参看SMO算法对应的论文3 实现。
四、代码实现
使用 Python 实现非线性支持向量机(SMO 算法)
import numpy as np
class SMO:
"""
支持向量机
序列最小优化算法实现(Sequential minimal optimization/SMO)
"""
def __init__(self, X, y, kernel, degree = 3, coef0 = 0.0, gamma = 1.0):
# 训练样本特征矩阵(N * p)
self.X = X
# 训练样本标签向量(N * 1)
self.y = y
# 拉格朗日乘子向量(N * 1)
self.alpha = np.zeros(X.shape[0])
# 误差向量,默认为负的标签向量(N * 1)
self.errors = -y
# 偏移量
self.b = 0
# 代价值
self.cost = -np.inf
# 核函数
self.kernel = kernel
# 核函数相关参数
self.degree = degree
self.coef0 = coef0
self.gamma = gamma
def fit(self, C = 1, tol = 1e-4):
"""
算法来自 John C. Platt 的论文
https://www.microsoft.com/en-us/research/uploads/prod/1998/04/sequential-minimal-optimization.pdf
"""
# 更新变化次数
numChanged = 0
# 是否检查全部
examineAll = True
while numChanged > 0 or examineAll:
numChanged = 0
if examineAll:
for idx in range(X.shape[0]):
numChanged += self.update(idx, C)
else:
for idx in range(X.shape[0]):
if self.alpha[idx] <= 0:
continue
numChanged += self.update(idx, C)
if examineAll:
examineAll = False
elif numChanged == 0:
examineAll = True
# 计算代价值
cost = self.calcCost()
if self.cost > 0:
# 当代价值的变化小于容许的范围时结束算法
rate = (cost - self.cost) / self.cost
if rate <= tol:
break
self.cost = cost
def update(self, idx, C = 1):
"""
对下标为 idx 的拉格朗日乘子进行更新
"""
X = self.X
y = self.y
alpha = self.alpha
# 检查当前拉格朗日乘子是否满足KKT条件,满足条件则直接返回 0
if self.checkKKT(idx, C):
return 0
if len(alpha[(alpha != 0)]) > 1:
# 按照|E1 - E2|最大的原则寻找第二个待优化的拉格朗日乘子的下标
jdx = self.selectJdx(idx)
# 对下标为 idx、jdx 的拉格朗日乘子进行更新,当成功更新时直接返回 1
if self.updateAlpha(idx, jdx, C):
return 1
# 当未更新成功时,遍历不为零的拉格朗日乘子进行更新
for jdx in range(X.shape[0]):
if alpha[jdx] == 0:
continue
# 对下标为 idx、jdx 的拉格朗日乘子进行更新,当成功更新时直接返回 1
if self.updateAlpha(idx, jdx, C):
return 1
# 当依然没有没有更新成功时,遍历为零的拉格朗日乘子进行更新
for jdx in range(X.shape[0]):
if alpha[jdx] != 0:
continue
# 对下标为 idx、jdx 的拉格朗日乘子进行更新,当成功更新时直接返回 1
if self.updateAlpha(idx, jdx, C):
return 1
# 依然没有更新时返回 0
return 0
def selectJdx(self, idx):
"""
寻找第二个待优化的拉格朗日乘子的下标
"""
errors = self.errors
if errors[idx] > 0:
# 当误差项大于零时,选择误差向量中最小值的下标
return np.argmin(errors)
elif errors[idx] < 0:
# 当误差项小于零时,选择误差向量中最大值的下标
return np.argmax(errors)
else:
# 当误差项等于零时,选择误差向量中最大值和最小值的绝对值最大的下标
minJdx = np.argmin(errors)
maxJdx = np.argmax(errors)
if max(np.abs(errors[minJdx]), np.abs(errors[maxJdx])) - errors[minJdx]:
return minJdx
else:
return maxJdx
def calcB(self):
"""
计算偏移量
分别计算每一个拉格朗日乘子不为零对应的偏移量后取其平均值
"""
X = self.X
y = self.y
alpha = self.alpha
alpha_gt = alpha[alpha > 0]
# 拉格朗日乘子向量中不为零的数量
alpha_gt_len = len(alpha_gt)
# 全部为零时直接返回 0
if alpha_gt_len == 0:
return 0
# b = y - Wx,具体算法请参考文章中的说明
X_gt = X[alpha > 0]
y_gt = y[alpha > 0]
s = 0
for idx in range(X_gt.shape[0]):
ss = 0
for jdx in range(X_gt.shape[0]):
ss += alpha_gt[jdx] * y_gt[jdx] * self.kernel(X_gt[jdx], X_gt[idx], self.degree, self.coef0, self.gamma)
s += y_gt[idx] - ss
return s / alpha_gt_len
def calcCost(self):
"""
计算代价值
按照文章中的算法计算即可
"""
X = self.X
y = self.y
alpha = self.alpha
cost = 0
for idx in range(X.shape[0]):
for jdx in range(X.shape[0]):
cost = cost + (y[idx] * y[jdx] * self.kernel(X[idx], X[jdx], self.degree, self.coef0, self.gamma) * alpha[idx] * alpha[jdx])
return np.sum(alpha) - cost / 2
def checkKKT(self, idx, C = 1):
"""
检查下标为 idx 的拉格朗日乘子是否满足 KKT 条件
1. alpha >= 0
2. alpha <= C
3. y * f(x) - 1 >= 0
4. alpha * (y * f(x) - 1) = 0
"""
y = self.y
errors = self.errors
alpha = self.alpha
r = errors[idx] * y[idx]
if (alpha[idx] > 0 and alpha[idx] < C and r == 0) or (alpha[idx] == 0 and r > 0) or (alpha[idx] == C and r < 0):
return True
return False
def calcU(self, idx, jdx, C = 1):
"""
计算拉格朗日乘子上界,使两个待优化的拉格朗日乘子同时大于等于0
按照文章中的算法计算即可
"""
y = self.y
alpha = self.alpha
if y[idx] * y[jdx] == 1:
return max(0, alpha[jdx] + alpha[idx] - C)
else:
return max(0.0, alpha[jdx] - alpha[idx])
def calcV(self, idx, jdx, C = 1):
"""
计算拉格朗日乘子下界,使两个待优化的拉格朗日乘子同时大于等于0
按照文章中的算法计算即可
"""
y = self.y
alpha = self.alpha
if y[idx] * y[jdx] == 1:
return min(C, alpha[jdx] + alpha[idx])
else:
return min(C, C + alpha[jdx] - alpha[idx])
def updateAlpha(self, idx, jdx, C = 1):
"""
对下标为 idx、jdx 的拉格朗日乘子进行更新
按照文章中的算法计算即可
"""
if idx == jdx:
return False
X = self.X
y = self.y
alpha = self.alpha
errors = self.errors
# idx 的误差项
Ei = errors[idx]
# jdx 的误差项
Ej = errors[jdx]
U = self.calcU(idx, jdx, C)
V = self.calcV(idx, jdx, C)
if U == V:
return False
Kii = self.kernel(X[idx], X[idx], self.degree, self.coef0, self.gamma)
Kjj = self.kernel(X[jdx], X[jdx], self.degree, self.coef0, self.gamma)
Kij = self.kernel(X[idx], X[jdx], self.degree, self.coef0, self.gamma)
# 计算 K
K = Kii + Kjj - 2 * Kij
oldAlphaIdx = alpha[idx]
oldAlphaJdx = alpha[jdx]
oldB = self.b
s = y[idx] * y[jdx]
if K > 0:
# 计算 jdx 的新拉格朗日乘子
newAlphaJdx = oldAlphaJdx + y[jdx] * (Ei - Ej) / K
if newAlphaJdx < U:
# 当新值超过上界时,修改其为上界
newAlphaJdx = U
if newAlphaJdx > V:
# 当新值低于下界时,修改其为下界
newAlphaJdx = V
else:
fi = y[idx] * (Ei + oldB) - oldAlphaIdx * Kii - s * oldAlphaJdx * Kij
fj = y[jdx] * (Ej + oldB) - s * oldAlphaIdx * Kij - oldAlphaJdx * Kjj
Vv = oldAlphaIdx + s * (oldAlphaJdx - V)
Uu = oldAlphaIdx + s * (oldAlphaJdx - U)
Vv = Vv * fi + V * fj + 0.5 * (Vv ** 2) * Kii + 0.5 * (V ** 2) * Kjj + s * V * Vv * Kij
Uu = Uu * fi + U * fj + 0.5 * (Uu ** 2) * Kii + 0.5 * (U ** 2) * Kjj + s * U * Uu * Kij
if Vv < Uu:
newAlphaJdx = V
elif Vv > Uu:
newAlphaJdx = U
else:
newAlphaJdx = oldAlphaJdx
if oldAlphaJdx == newAlphaJdx:
# 当新值与旧值相等时,判断为未更新,直接返回
return False
# 计算 idx 的新拉格朗日乘子
newAlphaIdx = oldAlphaIdx + s * (oldAlphaJdx - newAlphaJdx)
# 更新拉格朗日乘子向量
alpha[idx] = newAlphaIdx
alpha[jdx] = newAlphaJdx
oldB = self.b
# 重新计算偏移量
self.b = self.calcB()
# 重新计算误差向量
newErrors = []
for i in range(X.shape[0]):
newError = errors[i] + y[idx] * (newAlphaIdx - oldAlphaIdx) * self.kernel(X[idx], X[i], self.degree, self.coef0, self.gamma) + y[jdx] * (newAlphaJdx - oldAlphaJdx) * self.kernel(X[jdx], X[i]) - oldB + self.b
newErrors.append(newError)
self.errors = newErrors
return True
def predict(self, X):
fxs = []
for idx in range(len(X)):
fx = 0
for jdx in range(self.X.shape[0]):
fx += self.y[jdx] * self.alpha[jdx] * self.kernel(self.X[jdx], X[idx], self.degree, self.coef0, self.gamma)
fxs.append(fx + self.b)
return np.sign(fxs)
线性核函数支持向量机
# 线性核函数支持向量机
def linearKernel(x, z, degree = 3, coef0 = 0.0, gamma = 1.0):
return x.dot(z)
linearSmo = SMO(X, y, kernel = linearKernel)
linearSmo.fit()
多项式核函数支持向量机
# 多项式核函数支持向量机
def polynomialKernel(x, z, degree = 3, coef0 = 0.0, gamma = 1.0):
return np.power(gamma * x.dot(z) + coef0, degree)
polynomialSmo = SMO(X, y, kernel = polynomialKernel)
polynomialSmo.fit()
径向基核函数支持向量机
# 径向基核函数支持向量机
def rbfKernel(x, z, degree = 3, coef0 = 0.0, gamma = 1.0):
return np.exp(-gamma * np.power(np.linalg.norm(x - z), 2))
rbfSmo = SMO(X, y, kernel = rbfKernel)
rbfSmo.fit()
五、第三方库实现
scikit-learn4 实现
from sklearn.svm import SVC
# 线性核函数支持向量机
svc = SVC(kernel = "linear")
# 多项式核函数支持向量机
svc = SVC(kernel = "poly", gamma = 1)
# 径向基核函数支持向量机
svc = SVC(kernel = "rbf", gamma = 1)
# 拟合数据
svc.fit(X, y)
scikit-learn 内部使用的是 LIBSVM5 库,关于该库实现的细节可以参看这篇文章6 。
六、动画演示
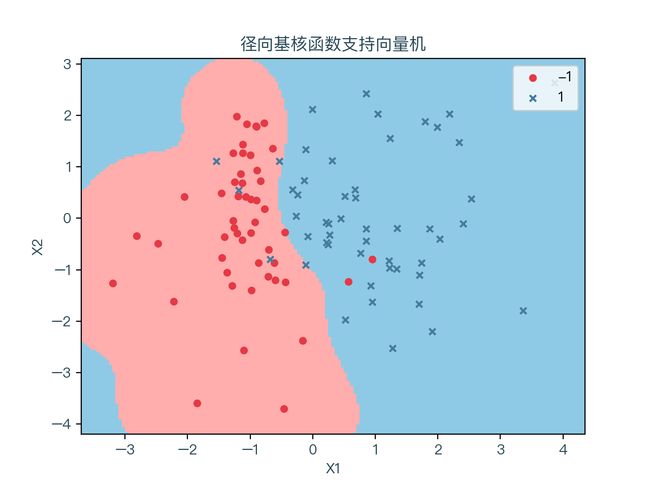
下面三个图分别展示了线性不可分的数据集针对不同的核函数的分类结果,红色表示标签值为 -1 的样本点,蓝色代表标签值为 1 的样本点。浅红色的区域为预测值为 -1 的部分,浅蓝色的区域则为预测值为 1 的部分:
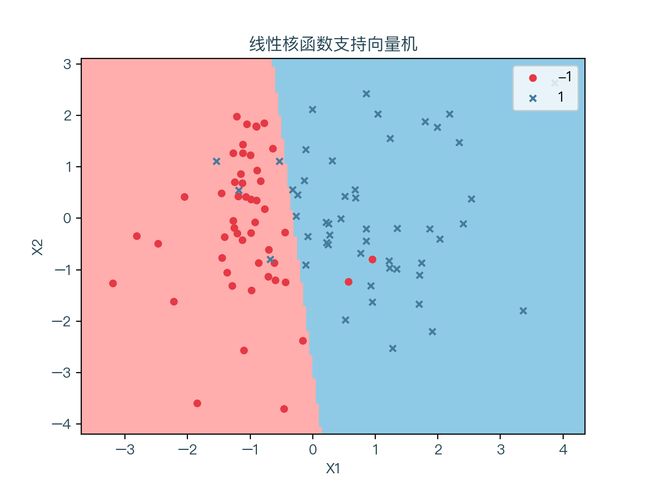
可以看到不同的核函数对于分类结果的影响很大,当不知道特征转换的的形式时,也就无法选择出合适的核函数,但通常情况下,非线性分类问题使用径向基核函数通过交叉验证的方式找出合适的参数即可。
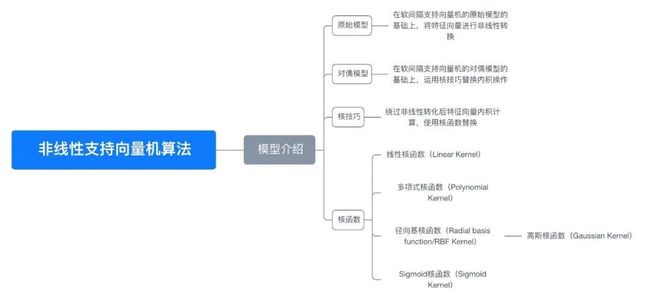
七、思维导图
八、参考文献
- https://en.wikipedia.org/wiki/Support-vector_machine#Nonlinear%20Kernels
- https://en.wikipedia.org/wiki/Kernel_method
- https://www.microsoft.com/en-us/research/uploads/prod/1998/04/sequential-minimal-optimization.pdf
- https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html
- https://www.csie.ntu.edu.tw/~cjlin/libsvm/
- https://github.com/Kaslanarian/libsvm-sc-reading/blob/main/libsvm.pdf
完整演示请点击这里
注:本文力求准确并通俗易懂,但由于笔者也是初学者,水平有限,如文中存在错误或遗漏之处,恳请读者通过留言的方式批评指正
本文首发于——AI导图,欢迎关注