二维泊松方程求解-SIP-最速下降法-共轭梯度
1. 直接解法:LU分解
在前面的内容中曾经提到,使用有限差分或有限体积法通过隐式离散得到 A ϕ = Q A\phi=Q Aϕ=Q的求解形式,其中 A A A为系数矩阵。在一定条件下, A A A能够通过因式分解为 A = L U A=LU A=LU,其中 L L L为下三角矩阵, U U U为上三角矩阵。
这样的分解方式在高斯消元中十分有用,对 A ϕ = Q A\phi=Q Aϕ=Q的求解可分为以下两步
U ϕ = Y L Y = Q U\phi=Y \\ LY=Q Uϕ=YLY=Q
2. 迭代法:incomplete LU decomposition
如果存在一个与 A A A近似的矩阵 M M M,对 M M M做LU分解,我们把这样的步骤称为 A A A的不完全LU分解,ILU,即
M = L U = A + N M=LU=A+N M=LU=A+N
其中 N N N为小量。
2.1. SIP
Stone提出了基于ILU且具有良好普适性的strongly implicit procedure (SIP),接下来我们简要介绍一下该算法。
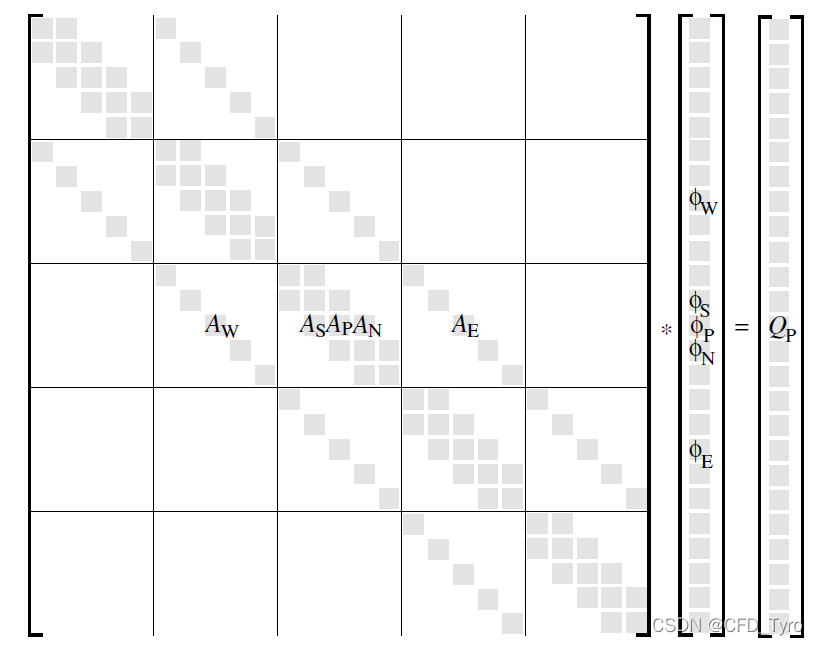
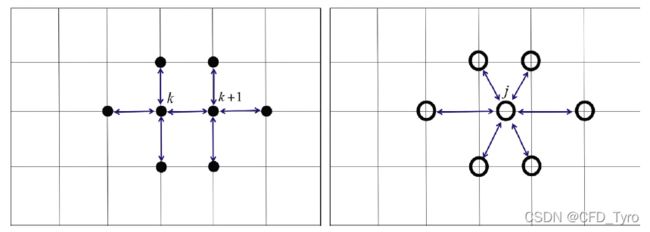
在ILU中,如果矩阵 A A A中的 ( i , j ) (i,j) (i,j)元素非零,那么 L L L或 U U U矩阵在该元素对应位置上的对角线非零。以下图所示的 A A A为五对角矩阵为例说明,图中非零元素占据五条对角线,那么对应的 L L L和 U U U各自包含三条对角线。
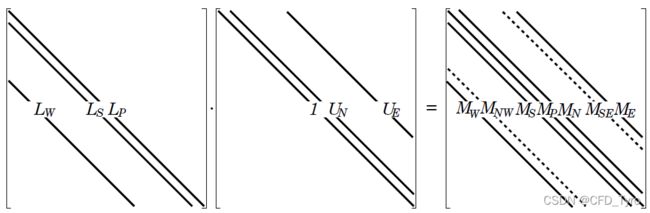
令 U U U主对角线上元素为1。可见, L L L与 U U U的乘积不可能为五对角矩阵,而是七对角矩阵,因此不可能还原为 A A A,而是 L U = M LU=M LU=M,如下图所示
令两次相邻迭代的差值为 δ \delta δ,则原代数方程组可写成
A ϕ n + 1 − A ϕ n = Q − A ϕ n A\phi^{n+1}-A\phi^n=Q-A\phi^n Aϕn+1−Aϕn=Q−Aϕn
A δ n = R n A\delta^{n}=R^n Aδn=Rn
矩阵 R R R为残差矩阵,为已知值。设想如果 A A A能够完全LU分解,那么便可以通过直接解法解出 δ n \delta^n δn,然后加到 ϕ n \phi^n ϕn求出 ϕ n + 1 \phi^{n+1} ϕn+1,整个过程只需一次迭代。可是根据前文的分析,五对角矩阵 A A A无法完全LU分解,因此Stone的目标变成了尽可能的让 L U LU LU的乘积 M M M接近 A A A。计算 M δ M\delta Mδ的乘积可得
M δ = L U δ = M P δ P + M S δ S + M N δ N + M E δ E + M W δ W + M N W δ N W + M S E δ S E M\delta=LU\delta=M_P\delta_P+M_S\delta_S+M_N\delta_N+M_E\delta_E+M_W\delta_W+\\ M_{NW}\delta_{NW}+M_{SE}\delta_{SE} Mδ=LUδ=MPδP+MSδS+MNδN+MEδE+MWδW+MNWδNW+MSEδSE
而 A δ A\delta Aδ的乘积只有五项,对比来看多出了最后两项。因此Stone认为应尽量地消去最后两项。对 δ N W \delta_{NW} δNW做Taylor展开
δ N W ≈ δ P − ∂ δ ∂ x ∣ P Δ x + ∂ δ ∂ y ∣ P Δ y \delta_{NW}\approx\delta_P-\frac{\partial \delta}{\partial x}\bigg|_P\Delta x+\frac{\partial \delta}{\partial y}\bigg|_P\Delta y δNW≈δP−∂x∂δ∣∣∣∣PΔx+∂y∂δ∣∣∣∣PΔy
∂ δ ∂ x ∣ P ≈ δ P − δ W Δ x \frac{\partial \delta}{\partial x}\bigg|_P\approx \frac{\delta_P-\delta_W}{\Delta x} ∂x∂δ∣∣∣∣P≈ΔxδP−δW
∂ δ ∂ y ∣ P ≈ δ N − δ P Δ y \frac{\partial \delta}{\partial y}\bigg|_P\approx \frac{\delta_N-\delta_P}{\Delta y} ∂y∂δ∣∣∣∣P≈ΔyδN−δP
代入前文的Taylor展开可得
δ N W ≈ − δ P + δ N + δ W \delta_{NW}\approx -\delta_P+\delta_N+\delta_W δNW≈−δP+δN+δW
δ S E ≈ − δ P + δ E + δ S \delta_{SE}\approx -\delta_P+\delta_E+\delta_S δSE≈−δP+δE+δS
Stone另外提出了校正系数 α \alpha α,其作用是 δ N W = α ( − δ P + δ N + δ W ) \delta_{NW}=\alpha(-\delta_P+\delta_N+\delta_W) δNW=α(−δP+δN+δW), δ S E \delta_{SE} δSE同理。
将这层关系替换到 M δ = R M\delta=R Mδ=R中可得:
( M P − α M N W − α M S E ) δ P + ( M E + α M S E ) δ E + ( M S + α M S E ) δ S + ( M N + α M N W ) δ N + ( M W + α M N W ) δ W = R P (M_P-\alpha M_{NW}-\alpha M_{SE})\delta_P+(M_E+\alpha M_{SE})\delta_E+\\ (M_S+\alpha M_{SE})\delta_S+(M_N+\alpha M_{NW})\delta_N+(M_W+\alpha M_{NW})\delta_W = R_P (MP−αMNW−αMSE)δP+(ME+αMSE)δE+(MS+αMSE)δS+(MN+αMNW)δN+(MW+αMNW)δW=RP
与 A δ = R A\delta=R Aδ=R对比可得矩阵 M M M和 A A A的关系。而 M M M是由 L L L和 U U U相乘而得,因此 L L L和 U U U也能够顺利求出。以上就是SIP算法的大致介绍,该算法中的“强隐式”体现在 L L L和 U U U的求解。
上文中图片来自《Computational Methods for Fluid Dynamics》, Ferziger
2.2. 代码实现
上一篇文章介绍了点迭代法,其特点是不涉及系数矩阵,内部结点 P P P仅和上下左右四点相关,换句话说我们只要判断 ( i , j ) (i,j) (i,j)处的 P P P点的上下左右四个结点在模拟区域中的位置即可。
本文介绍的SIP方法显然是对系数矩阵进行操作,这更符合工程应用中求解CFD的习惯,因为实际问题往往是网格量大、编号无规则、代数矩阵稀疏。
同样求解上一篇文章中的二维泊松方程,模拟区域 x y xy xy方向均存在 N N N个结点,故结点数或变量数为 N × N = N 2 N\times N=N^2 N×N=N2,因此系数矩阵 A A A的大小为 N 2 × N 2 N^2\times N^2 N2×N2,变量数和矩阵大小切勿弄混。
程序中我们采用一维数组对结点编号,即 ϕ 1... N 2 \phi_{1...N^2} ϕ1...N2,对于边界上的结点,例如 ϕ 1 , 2... N \phi_{1,2...N} ϕ1,2...N,其值已知,因为Dirichlet边界条件。下面是计算步骤:
- 构建系数矩阵 A A A和源项 Q Q Q,注意,第一个结点在程序中的编号从0开始,故右边界的结点编号为 N − 1 N-1 N−1。边界结点 k k k在 A A A中的值为1,即 A [ k , k ] = 1 A[k,k]=1 A[k,k]=1, Q [ k ] Q[k] Q[k]直接为边界上的值。内部结点 i i i的 A [ i , i ] = 4 A[i,i]=4 A[i,i]=4,其上下左右四个结点的系数为-1,推导过程见上一篇文章。
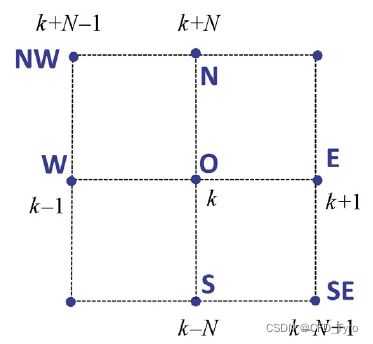
- 利用 A A A构建 L L L和 U U U矩阵,这部分计算流程见Sandip Mazumder所著《Numerical Methods for Partial Differential Equations》,需要注意的是书中几个变量的定义(书中公式3.38和3.57),例如向量 B B B的第 k k k个值表示编号为 k k k的结点的正下方邻居结点的系数。
- 给定 ϕ \phi ϕ初值,我在程序中直接将 Q Q Q的值作为 ϕ \phi ϕ的初值。然后计算 R = Q − A ϕ R=Q-A\phi R=Q−Aϕ并计算向量 R R R的二范数,若二范数小于0.01则认为收敛。接着计算 L Y = R LY=R LY=R, L L L为下三角, Y 0 Y_0 Y0可以直接求出,因此可以快速的求出 Y Y Y;接着计算 U δ = Y U\delta =Y Uδ=Y, U U U为上三角, δ [ − 1 ] \delta[-1] δ[−1]可以直接求出, δ \delta δ可以求出。接着 ϕ n + 1 = ϕ + δ \phi^{n+1}=\phi+\delta ϕn+1=ϕ+δ,完成更新。
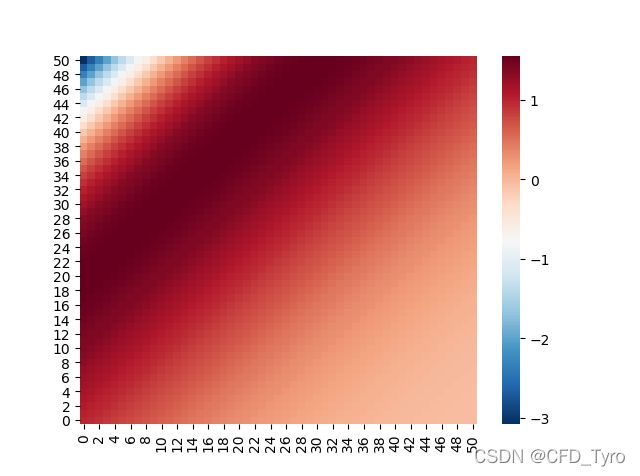
2.3. 计算结果
N=51,二范数收敛标准0.01,Stone系数 α = 0.9 \alpha=0.9 α=0.9,需要说明的是,这里的迭代次数与点迭代的计算方式完全不同,但复杂度均与结点数目成正比。
| Method | Iteration number |
|---|---|
| SIP | 182 |
3. 最速下降法
Method of Steepest Descent (MSD),该算法思想是将代数方程组的求解转化为求二次型相关的极值问题。例如,对于 a x = b ax=b ax=b,我们可以将其看作二次函数 y = 0.5 a x 2 − b x + c y=0.5ax^2-bx+c y=0.5ax2−bx+c求极值问题,也就是对二次函数求导并求导数为0对应的值,这样就解出了 x x x
将这样的思路转换到代数方程组求解问题,对于 A ϕ = Q A\phi=Q Aϕ=Q,如果 A A A是正定矩阵或负定,则我们可以构造“二次函数”
f ( ϕ ) = 1 2 ϕ T A ϕ − ϕ T Q − c f(\phi)=\frac{1}{2}\phi^TA\phi-\phi^TQ-c f(ϕ)=21ϕTAϕ−ϕTQ−c
上述函数的极值就是原代数方程组的解。其中 ϕ = [ ϕ 1 , ϕ 2 , . . . , ϕ m ] \phi=[\phi_1,\phi_2,...,\phi_m] ϕ=[ϕ1,ϕ2,...,ϕm]
对上述函数求导
∇ f ( ϕ ) = [ ∂ f ∂ ϕ 1 ∂ f ∂ ϕ 2 ⋯ ∂ f ∂ ϕ m ] = 1 2 A T ϕ + 1 2 A ϕ − Q = 0 \nabla f(\phi)= \left[ \begin{matrix} \frac{\partial f}{\partial \phi_1} \\ \frac{\partial f}{\partial \phi_2} \\ \cdots \\ \frac{\partial f}{\partial \phi_m} \end{matrix} \right] =\frac{1}{2}A^T\phi+\frac{1}{2}A\phi-Q=0 ∇f(ϕ)=⎣⎢⎢⎢⎡∂ϕ1∂f∂ϕ2∂f⋯∂ϕm∂f⎦⎥⎥⎥⎤=21ATϕ+21Aϕ−Q=0
如果矩阵 A A A对称,则 A T = A A^T=A AT=A
MSD适用范围为:矩阵 A A A对称且正定或负定,当满足这个条件时,求上述二次函数的极值便等价于求 A ϕ = Q A\phi=Q Aϕ=Q
3.1. MSD求解
- 给定初值 ϕ n \phi^n ϕn,代入矩阵求解残差 R n R^n Rn
( ∇ f ) n = − R n = Q − A ϕ n (\nabla f)^n=-R^n=Q-A\phi^n (∇f)n=−Rn=Q−Aϕn - 沿着梯度下降的方向进行更新,其中 α \alpha α为沿梯度方向走的步长
ϕ n + 1 = ϕ n − α n ( ∇ f ) n = ϕ n + α n R n \phi^{n+1}=\phi^n-\alpha^n(\nabla f)^n=\phi^n+\alpha^n R^n ϕn+1=ϕn−αn(∇f)n=ϕn+αnRn - 计算步长 α \alpha α
MSD的思想是沿着初始计算的梯度方向一直走,在刚开始走的过程中,函数值一定是单调递增或递减,当走到某一个点,在这个点往后的函数值与之前的变化规律不同,这时MSD认为应该重新计算梯度。举个例子,下山过程,从山顶开始沿着最大梯度下降的方向行进,到走到某个地方发现眼前不再是下坡,这时就需要重新看一看此处哪个方向的梯度最大,然后改变方向继续走。
用数学的语言来说, f f f随 α \alpha α的变化达到拐点时就需要重新计算梯度,因此也变成了寻找极值的问题
∂ f ∂ α ∣ n + 1 = 0 \frac{\partial f}{\partial \alpha}\bigg|^{n+1}=0 ∂α∂f∣∣∣∣n+1=0
由链式求导法则
[ ∂ f ∂ ϕ 1 ∂ ϕ 1 ∂ α + ∂ f ∂ ϕ 2 ∂ ϕ 2 ∂ α + . . . + ∂ f ∂ ϕ N ∂ ϕ N ∂ α ] n + 1 = 0 \left[ \frac{\partial f}{\partial\phi_1}\frac{\partial\phi_1}{\partial\alpha} + \frac{\partial f}{\partial\phi_2}\frac{\partial\phi_2}{\partial\alpha} +...+ \frac{\partial f}{\partial\phi_N}\frac{\partial\phi_N}{\partial\alpha} \right]^{n+1}=0 [∂ϕ1∂f∂α∂ϕ1+∂ϕ2∂f∂α∂ϕ2+...+∂ϕN∂f∂α∂ϕN]n+1=0
ϕ \phi ϕ和 α \alpha α的关系由上一步的迭代通式给出,代入上式可得
[ ∂ f ∂ ϕ 1 ∣ n + 1 R 1 n + ∂ f ∂ ϕ 2 ∣ n + 1 R 2 n + . . . + ∂ f ∂ ϕ N ∣ n + 1 R N n ] n + 1 = 0 \left[ \frac{\partial f}{\partial\phi_1}\bigg|^{n+1}R_1^n + \frac{\partial f}{\partial\phi_2}\bigg|^{n+1}R_2^n +...+ \frac{\partial f}{\partial\phi_N}\bigg|^{n+1}R_N^n \right]^{n+1}=0 [∂ϕ1∂f∣∣∣∣n+1R1n+∂ϕ2∂f∣∣∣∣n+1R2n+...+∂ϕN∂f∣∣∣∣n+1RNn]n+1=0
而 ∇ f \nabla f ∇f与 R R R的关系已在第一步给出,因此上式可以整理为
− ( R n + 1 ) T R n = − ( Q − A ϕ n + 1 ) T R n = 0 -(R^{n+1})^T R^n=-(Q-A\phi^{n+1})^TR^n=0 −(Rn+1)TRn=−(Q−Aϕn+1)TRn=0
把 ϕ n + 1 \phi^{n+1} ϕn+1和 ϕ n \phi^n ϕn的关系代入上式并整理可得 α \alpha α的计算通式
α n = ( R n ) T R n ( R n ) T A R n \alpha^n=\frac{(R^n)^T R^n}{(R^n)^T A R^n} αn=(Rn)TARn(Rn)TRn
3.2. 结果讨论
N=51,二范数收敛标准0.01,迭代及其缓慢,迭代600次二范数为0.13,还远远达不到收敛标准。
3.3. 举例
A ϕ = [ 3 2 2 6 ] [ ϕ 1 ϕ 2 ] = Q = [ 2 − 8 ] A\phi= \left[ \begin{matrix} 3 & 2 \\ 2 & 6 \\ \end{matrix} \right] \left[ \begin{matrix} \phi_1 \\ \phi_2 \\ \end{matrix} \right] =Q= \left[ \begin{matrix} 2 \\ -8 \\ \end{matrix} \right] Aϕ=[3226][ϕ1ϕ2]=Q=[2−8]
解析解为 [ 2 , − 2 ] [2,-2] [2,−2]
3.3.1. 构造二次函数
f ( ϕ 1 , ϕ 2 ) = 3 2 ϕ 1 2 + 2 ϕ 1 ϕ 2 + 3 ϕ 2 2 − 2 ϕ 1 + 8 ϕ 2 + c f(\phi_1,\phi_2)=\frac{3}{2}\phi_1^2+2\phi_1\phi_2+3\phi_2^2-2\phi_1+8\phi_2+c f(ϕ1,ϕ2)=23ϕ12+2ϕ1ϕ2+3ϕ22−2ϕ1+8ϕ2+c
3.3.2. 求偏导
∇ f = [ 3 ϕ 1 + 2 ϕ 2 − 2 2 ϕ 1 + 6 ϕ 2 + 8 ] \nabla f= \left[ \begin{matrix} 3\phi_1+2\phi_2-2 \\ 2\phi_1+6\phi_2+8 \\ \end{matrix} \right] ∇f=[3ϕ1+2ϕ2−22ϕ1+6ϕ2+8]
3.3.3. 更新梯度
令初值为 ϕ n = [ − 2 , − 2 ] \phi^n=[-2,-2] ϕn=[−2,−2],则
∇ f n = [ − 12 − 8 ] \nabla f^n= \left[ \begin{matrix} -12 \\ -8 \\ \end{matrix} \right] ∇fn=[−12−8]
4. 共轭梯度法
最速下降法中,后一次梯度方向垂直于前一次梯度方向,这种“台阶式”的迭代模式会使迭代效率大大下降,前文迭代600次,残差也仍未达到指定要求。
共轭梯度法(Conjugate gradient, CG)与MSD的区别是,后一次梯度方向并不垂直于前一次,而是前一次与当前计算结果的线性叠加,因此能够提高迭代效率。
4.1. 计算流程
- 给定初始值 ϕ 0 \phi^0 ϕ0
- 计算残差向量 R 0 R^0 R0
- 初始化方向向量 D 0 D^0 D0,令 D 0 = R 0 D^0=R^0 D0=R0
- 用方向向量计算步长 α n + 1 \alpha^{n+1} αn+1
α n + 1 = ( R n ) T R n ( D n ) T A D n \alpha^{n+1}=\frac{(R^n)^T R^n}{(D^n)^T A D^n} αn+1=(Dn)TADn(Rn)TRn - 更新 ϕ n + 1 = ϕ n + α n + 1 D n \phi^{n+1}=\phi^n+\alpha^{n+1}D^n ϕn+1=ϕn+αn+1Dn
- 计算新的残差向量 R n + 1 = Q − A ϕ n + 1 R^{n+1}=Q-A\phi^{n+1} Rn+1=Q−Aϕn+1以及向量二范数
- 计算残差向量与方向向量叠加的权重 β \beta β
β n + 1 = ( R n + 1 ) T R n + 1 ( R n ) T R n \beta^{n+1}=\frac{(R^{n+1})^TR^{n+1}}{(R^n)^TR^n} βn+1=(Rn)TRn(Rn+1)TRn+1 - 计算新的方向向量
D n + 1 = R n + 1 + β n + 1 D n D^{n+1}=R^{n+1}+\beta^{n+1}D^n Dn+1=Rn+1+βn+1Dn - 判断第6步计算的二范数是否达到收敛要求,若不,则回到第4步
4.2. 结果讨论
N=51,二范数收敛标准0.01
| Method | Iteration number |
|---|---|
| CG | 81 |
4.3. 代码
使用python实现上述三种方法(SIP,MSD,CG)代码,代码链接
4.4. 总结和比较
从以上介绍中可以看出,SIP、MSD、CG均要求系数矩阵 A A A是对称矩阵,但在实际问题中往往达不到这种要求,比如遇到非均匀网格排列、非结构化网格、曲线网格、传递系数非定值等情况时, A A A不会对称。
为了解决CG方法只能应用于对称矩阵的情况,研究者提出了有代表性的CGS和BiCG方法,前者是Conjugate gradient squared,后者是Bi-Conjugate gradient
前文说过,只有系数矩阵对称时,“二次函数”的极值问题才能等价于求解 A X = Q AX=Q AX=Q,如果不对称,则需要多计算 A T A^T AT,BiCG方法就是多计算了 A T A^T AT。该方法是OpenFOAM中常见的非对称矩阵求解器之一。
CGS并不打算求 A T A^T AT,而是在CG的基础上又加入了一个共轭方向向量 D ∗ D^{*} D∗,这里不再多做讨论
5. 预处理Preconditioning
影响迭代收敛的因素有很多,目前达成共识的是降低系数矩阵 A A A的条件数会有利于迭代收敛。因此预处理的目的就是将原始矩阵 A A A做某些处理从而降低其条件数。
处理方法就是在 A ϕ = Q A\phi=Q Aϕ=Q两边同乘矩阵 M − 1 M^{-1} M−1
M − 1 A ϕ = M − 1 Q M^{-1}A\phi=M^{-1}Q M−1Aϕ=M−1Q
上式中的 M − 1 M^{-1} M−1被称为preconditioner即预处理矩阵。处理效果就是新矩阵 M − 1 A M^{-1}A M−1A的条件数小于 A A A。最优的 M − 1 M^{-1} M−1自然是 A − 1 A^{-1} A−1,然而这个矩阵很难求出,解出该矩阵意味着直接获得了方程的解。因此 M − 1 M^{-1} M−1越接近 A − 1 A^{-1} A−1越好。
常用的preconditioner可分为以下几类:
- 基于经典迭代算法的
a. Jacobi: A A A的对角线组成的矩阵,即 M = D = d i a g ( A ) M=D=diag(A) M=D=diag(A)
b. GS - 基于不完全分解的ILU
a. ILU(0)
b. ILU(n)
c. ILUT - 基于不完全Cholesky分解
- 多项式
6. 多重网格法Multigrid Method
多重网格法可以理解为其目的是降低系数矩阵的特征值。网格越大即结点间距越大,系数矩阵特征值越小,意味着粗网格下的收敛速度快,本文和上一篇文章都验证了这个现象,结点越少收敛越快,但精度越低。
根据使用场景,多重网格法可以分为两种:
- GMG: Geometric MultiGrid
- AMG: Algebraic MultiGrid
6.1. GMG
该方法采用一系列大小不同的网格(不同间距的结点)来离散模拟区域。
- 方程离散。在每一套网格上都做一遍方程离散
- 光滑操作
a.smoother:选择一款简单的代数方程组求解器作为smoother,比如本文和上文介绍过的六种求解器,GS求解器是一款常用的smoother
b.smoothing:采用上述求解器求解最细网格的离散方程
c.partial convergence:不必完全收敛,达到一定精度即可。通常使得残差向量的二范数下降两个数量级即可。 restriction:将细网格的残差向量赋值给粗网格。在粗网格上继续迭代计算,此时要达到收敛标准即full convergenceprolongation:将粗网格结果加上原来细网格的计算结果作为细网格新的值。- 检查是否收敛
通常网格层数越多,所需的迭代会越少。
6.2. AMG
借用GMG的概念。GMG必须要对模拟区域进行多重网格划分,但是AMG并没有进行多重划分,而只是在一套网格上构建离散方程,然后通过融合和映射得到其他层网格的离散方程。该方法的关键步骤是融合。
6.2.1. 融合agglomeration
由于上述方程是在细网格结点上离散的,那么粗网格结点就需要将周围几个细网格结点融合起来。如下图所示