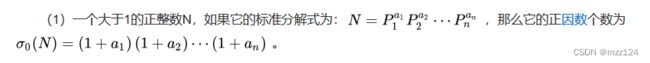CSDN竞赛—第五期题解与感想

一、题解

题目来自赛后题解报告，很可惜只有题目而没写样例与数据范围，下面的样例和范围都是凭记忆写的

1. 寻因找祖

【题目描述】

寻找因子个数为 n 的最小整数 x.

【输入格式】

输入一个整数 n 表示因子个数

【输出格式】

输出一个整数表示 x

【输入样例】

3

【输出样例】

4

【样例说明】

4 是拥有三个 因子的最小整数，三个因子分别是：1，2，4

【数据规模】

1 <= n <= 1000

解题思路

可以先了解下唯一分解定理关于因子个数的部分，也叫算数基本定理，平常也会直接说是质因数分解：

任何一个正整数都可以分解成多个质数相乘的形式，这个分解过程就叫质因数分解，比如: 60 = 2 * 2 * 3 * 5 = 2² * 3¹ * 5¹ ，将所有质因数的指数 +1 再相乘即为因子个数，60 的因子数为 (2 + 1) * (1 + 1) * (1 + 1) = 12

于是据此可以想到，根据质因数来构建一个 因子数为 n 的整数，比如 2 * 2 = 4 是因子数为 3 的整数，2 * 2 * 2 = 8 是因子数为 4 的整数，而 2 * 3 = 6 因子数也为 4 且比 8 更小，所以我们要做的就是找出最优的质因数组合，使结果最小

这一过程可以用递归来实现，每次递归选用一个质数并指定其指数，使最终的因子数为 n，在多种组合中找出最优（最小）解

AC代码

可以很容易想到，2^n-1 一定满足 n 个因子数，但可能不是最优解，所以可以用 2^n-1 作为上界，来不断缩小解

由于指数会很大，所以选用 double 来运算，最终答案一定不是一个超大的数，不然没法输出，所以不用担心 double 的精度问题，double 主要用来比较大小

代码是在题目的模板里写的，觉得答案也不会太小，就把 main 函数里的 int 改为了 long long，主要代码可以只看 solution 函数

#include 
#include 
#include 
#include 
#include 

using namespace std;
// 质数表，50 以内的质数就够了（小学背过）
double p[] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47};
// dfs(n, idx) 表示：构建因子数为 n，起始质数为 p[idx]
double dfs(long long n, long long idx) {
    if (n == 1) return 1;
    double ret = pow(p[idx], n - 1);	// 以当前质数 p[idx] 的 n - 1 次方作为最大可行的答案
    for (long long i = 2; i < n; i ++) {
    	// 枚举当前质数 p[idx] 可行的指数(+1)，再递归下一质数
        if (n % i == 0) {
            ret = min(ret, pow(p[idx], i - 1) * dfs(n / i, idx + 1));
        }
    }
    return ret;
}
double solution(long long n){
    return dfs(n, 0);
}


signed main() {
    long long n;
    std::cin>>n;
    long long result = solution(n);
    std::cout<<result<<std::endl;
    return 0;
}

题外话

蓝桥杯有一道真题考过同样的题面，只不过是一道填空题，而且样例很小，是算因子数为 100 的最小整数，暴力就能得出答案。

但当时做到这一题时就多费了会儿劲，推出了现在的结论，所以比赛时看到题目就直接有思路了，如果比赛现场推的话，还是有点难度的。

另外关于这道题，有一个貌似正确的错误思路，就是对 n 进行质因数分解，再根据分解结果分配质数和指数

比如 n = 12 = 2 * 2 * 3 = (1 + 1) * (1 + 1) * (2 + 1)，所以需要三个质数且指数分别 1，1，2，按贪心思想较小的指数分配较大的指数，所以的到 2² * 3¹ * 5¹ = 60，因子数为 12 的最小整数就是 60

多数情况下这个做法是可以得出正确答案的，但也有个例，比如 n = 8 = 2 * 2 * 2 = (1 + 1) * (1 + 1) * (1 + 1)，分配质数为 2¹ * 3¹ * 5¹ = 30，但 30 并不是最优解，2³ * 3¹ = 24 才是

2. 通货膨胀-x国货币

【题目描述】

X 国发行货币最高面额为 n。 次高面额为 n 的因子。 以此类推。 X 国最多发行多少种货币。

【输入格式】

输入一个整数 n 表示最高面额

【输出格式】

输出一个整数表示答案

【输入样例】

10

【输出样例】

3

【样例说明】

可以发行面额为 10，5，1 或者 10，2，1 三种面额的货币

【数据规模】

1 <= n <= 10⁶

解题思路

也是考质因数分解，不过比第一题简单多了

每个整数都可以分解成多个质数相乘，所以每次可以从分解式中拿掉一个质因数，作为次高面额，不断重复此过程

所以找出质因数的个数，再 +1 即为答案（因为还有面额 n 本身）

比如 n = 8 = 1 * 2 * 2 * 2，每次拿掉一个 2，可以拿掉 3 次，再算上 n 本身，所以最多发行 4 种货币，分别是 8，4，2，1

AC代码

#include 
#include 
#include 
#include 
#include 

using namespace std;
const int N = 1E6 + 5;

int solution(int n) {
    int ans = 0;
    // n 可能是质数，为减小复杂度只循环到根号 n
    for (int i = 2; i * i <= n; i++) {
        while (n % i == 0) {
            ans++;
            n /= i;
        }
    }
    // 最后 n 不为 1 说明剩下的 n 也是质因数，答案 +1
    if (n != 1) ans++;
    return ans + 1;
}

int main() {
    int n;
    std::cin >> n;
    int result = solution(n);
    std::cout << result << std::endl;
    return 0;
}

3. 莫名其妙的键盘

【题目描述】

有一个神奇的键盘，你可以用它输入a 到 z 的字符，然而每当你输入一个元音字母 (a,e,i,o,u其中之一)的时候，已输入的字
符串会发生一次反转！ 比方说，当前输入了 tw，此时再输入一个 o，此时屏幕上的字符串 two 会反转成 owt。 现给出一个
字符串，若用该键盘输入，有多少种方法可以得到？

【输入格式】

输入一个字符串表示键盘需要输入的内容

【输出格式】

输出一个整数表示输入可行的方法数

【输入样例】

ac

【输出样例】

2

【样例说明】

输入顺序可以是 ac 也可以是 ca

【数据规模】

输入的字符串长度最大为 200

解题思路

为便于处理，先给每个字符打上标记，是元音字母则为 1，否则为 0，也代表是否会令输入的内容翻转

逆向思维一下，对于字符串考虑最后输入的字符是谁，可以发现只能是开头或末尾的字符

如果最后输入末尾的字符，那么这个字符一定不是元音，且其他字符已经按顺序输入完成了
如果最后输入开头的字符，那么这个字符一定是元音，且其他字符已经按翻转后的顺序输入完成，输入最后的字符后再次翻转完成输入

为方便说明，我们将原本的顺序称为正序，翻转后的顺序称为逆序

总结出下面几个规则：

1. 要正序输入字符串，且最后输入的是末尾字符：必须满足末尾字符不为元音，且其余字符能够正序输入
2. 要正序输入字符串，且最后输入的是开头字符：必须满足开头字符为元音，且其余字符能够逆序输入
3. 要逆序输入字符串，且最后输入的是末尾字符：必须满足末尾字符为元音，且其余字符能够正序输入
4. 要逆序输入字符串，且最后输入的是开头字符：必须满足开头字符不为元音，且其余字符能够逆序输入

接下来无脑递归，记录字符顺序存入 set 去重，最后 set 中的字符串个数即为答案

参考代码

由于每次递归只会减少最左侧或最右侧的字符，所以可以用 i 和 j 表示剩余字符的下标区间

#include 
#include 
#include 
#include 
#include 

using namespace std;
int a[205];
string s;
set<string> st;

// 递归处理 s[i ~ j]，f 为 0 表示要正序，为 1 要逆序，tmp 记录字符顺序
void dfs(int i, int j, int f, string tmp) {
    if (i > j) {	// 所以字符处理完毕
        st.insert(tmp);	// 字符顺序添加到集合
        return;
    }
    if (f == 0) {	// 要正序输入剩余字符
        if (a[j] == 0)	// 末尾不是元音
            dfs(i, j - 1, 0, tmp + s[j]);	// 递归：要正序输入 s[i ~ j-1]
        if (a[i] == 1)	// 开头是元音
            dfs(i + 1, j, 1, tmp + s[i]);	// 递归：要逆序输入 s[i+1 ~ j]
    } else {		// 要逆序输入剩余字符
        if (a[i] == 0)	// 开头不是元音
            dfs(i + 1, j, 1, tmp + s[i]);	// 递归：要逆序输入 s[i+1 ~ j]
        if (a[j] == 1)	// 末尾是元音
            dfs(i, j - 1, 0, tmp + s[j]);	// 递归：要正序输入 s[i ~ j-1]
    }
}
// 判断是否为元音
bool check(char ch) {
    return ch == 'a' || ch == 'e' || ch == 'i' || ch == 'o' || ch == 'u';
}

int solution(std::string str) {
    s = str;
    int n = s.length();
    for (int i = 0; i < n; i++) {
        a[i] = check(str[i]);
    }
    dfs(0, n - 1, 0, "");	// 目标：正序输入所以字符
    return st.size();		// 集合的元素个数
}

int main() {
    std::string str;
    std::cin >> str;
    int result = solution(str);
    std::cout << result << std::endl;
    return 0;
}

这题比赛时只过了 50% 的样例，因为当时多加了个条件，当时以为末尾字符是元音也可以最后输入，只要其他的是逆序就可以，其实是错的，这样也能拿一半份，属实是运气好了

这是赛后改正过的代码，不过不知道哪里可以评测，不知道能不能 AC，如果有错还请大佬指正

4. 三而竭

【题目描述】

一鼓作气再而衰三而竭。 小艺总是喜欢把任务分开做。 小艺接到一个任务，任务的总任务量是 n。 第一天小艺能完成 x 份
任务。 第二天能完成 x / k 。 。。。 第 t 天能完成 x / (k ^ (t - 1))。 小艺想知道自己第一天至少完成多少才能完成最后的任务。

【输入格式】

输入两个整数用空格间隔，分别代表题中的 n 和 k

【输出格式】

输出一个整数表示答案

【输入样例】

8 2

【输出样例】

5

【样例说明】

第一天完成 5 份，第二天完成 5 / 2 = 2 份，第三天完成 2 / 2 = 1 份，所有任务完成

【数据规模】

貌似是 n <= 10⁹，不太记得了，只是按二分的复杂度，这个规模是正常的

解题思路

这题真的一眼二分了，题面最后的问句就是二分的经典话术，在可行中找最小，就是找可行与不可行的边界

之所以能二分是因为结果具有单调性，第一天做完的任务数越大，最后能完成所有任务的可能性就越大

左边界可以为 0 或 1，第一天就摆烂肯定不可行，右边界可以是 n，第一天就把任务做完了，套一下二分的模板就可以了

AC代码

#include 
#include 
#include 
#include 

using namespace std;
typedef long long ll;

// 判断第一天完成 x 份任务是否可行，long long 避免超 int 范围
bool check(ll x, int n, int k) {
    int ans = x;
    while (ans < n) {
        x /= k;
        if (x == 0) return false;
        ans += x;
    }
    return true;
}
int solution(std::vector<int>& vec){
    int n = vec[0], k = vec[1];
    ll l = 1, r = n;
    while (l < r) {
        ll mid = (l + r) / 2;
        if (check(mid, n, k))
            r = mid;
        else
            l = mid + 1;
    }
    return r;
}

int main() {
    std::vector<int> vec;
    std::string line_0, token_0;
    getline(std::cin >> std::ws,line_0);
    std::stringstream tokens_0(line_0);
    while(std::getline(tokens_0, token_0, ' ')){
        vec.push_back(std::stoi(token_0));
    }
    int result = solution(vec);
    std::cout<<result<<std::endl;
    return 0;
}

二、赛后总结

我个人的竞赛经历只有力扣周赛和蓝桥杯，勉强算半个竞赛生吧，能力嘛应该算比上不足比下有余吧……。好在对竞赛饶有兴趣，偶然才发现 csdn 也有比赛，而且已经办了四期了，可惜没有早点发现，这是第一次参加，接下来对这次比赛吐槽一番

1. 比赛赛制

我所了解的比赛中，力扣周赛是 ACM 赛制，能即时评测，按得分和罚时排名
蓝桥杯是 OI 赛制，不能即时评测，只能提交代码，等比赛结束后统一改卷评测，按分数排名（就和传统试卷性质一样）
这次的CSDN竞赛是 IOI 赛制，可以即时评测，能看到得分，不限评测次数，采用这种规则的有浙江大学的天梯赛，和 PAT 认证。

我是比较喜欢这种赛制的，因为比较放松，提交的时候不用怕写错，因为没有罚时

不过 IOI 应该以得分最高的一次提交计入总成绩，但这次的竞赛后看到有人反映，是按照最后一次提交计入成绩的（比赛时我就怕出现这种情况，所以最后又都提交了一下）。这个机制应该要改的，毕竟改了代码之后发现得分低了，还要再改回去提交，挺麻烦的

2. 题目难度

对于算法竞赛来说，这次的题目难度应该是适中的，至少不是很难。但对于不了解竞赛相关的同学还是有难度，csdn 毕竟不是算法平台，如果要考虑大部分用户的话，起码来一道签到题吧

这次的四道题中，个人觉得 2，4 题是比较简单的，1，3 题较难，之后可以考虑下按难度顺序排题号

另外，这次第 1，2 题都考到了质因数相关的知识点，如果有选手不了解这个点的话就可能直接葬送了两道题，而且一共才四道题

能否把每次竞赛后的题目都放进题库，一方面供赛前练习，另一方面供赛后复盘，了解自身的不足

还有，这次题目都比较简短易懂，简短的语句表达出准确的题意是难得可贵的优点，希望以后也能保持这样（我所了解的力扣和蓝桥杯都常有阅读理解题，极搞心态）

3. 竞赛体验

这次比赛恐怕大多数人都体验很差吧，哈哈，看 bug反馈区的评论就能看出来了，我也不例外，满意的话就不会吐槽这么多了

---

首先就是开赛了服务器还没好，等了好一段时间，服务器出问题应该是小概率事件，就不多说了，希望以后不会了

---

说一下监考系统，复制粘贴和离开页面都会检测报警，最多各 20 次，看成绩报告里离开页面的时长也会记录，不知道离开太长时间会不会被判违规
主要是说规定不能用本地的 IDE 编写和调试代码，这是很头疼的事儿，尤其是竞赛页面那么简陋的情况下……

我参加力扣周赛时也很少用到本地的 IDE，但至少力扣的环境用起来还不错
建议 csdn 优化一下界面，提高一下编码体验，或者更改一下规则，比如允许离开页面最多 30 分钟，像现在的监考系统只能是防君子不防小人

另外界面内复制粘贴自己写的代码也会被检测，有点难受，能不能做一个界面内的剪切板，不同于系统的剪切板，比如选中文本即复制，鼠标中键粘贴这样

---

再说一下影响心态的部分，在不同题目中切换时，题目中的已经写好的代码可能会变得混乱，在这次比赛中我在第一题按 ctrl + z 回退代码时，代码突然变成了另一题的，搞到最后只能重写一遍，而且看前几期竞赛有人分享的文章，好像也有人遇到了一样的状况
还有我在调试第三题的时候，运行测试样例却没有输出 debug 的内容，仔细一看发现运行的是第一题的代码，搞了好久才恢复正常
不太清楚是我浏览器的缓存问题还是竞赛系统问题，总之是挺搞心态的

总结

同志仍须努力！

看得出来CSDN竞赛搞得还不太成熟，感觉还没有投入太多资源在这方面，不过官方还在很积极的收集反馈，以后应该会越来越好，我还是很希望之后能继续参加 CSDN 竞赛的。毕竟蒟蒻打不过别的地方的大佬