共轭梯度法(Conjugate Gradients)(1)
最近在看ATOM,作者在线训练了一个分类器,用的方法是高斯牛顿法和共轭梯度法。看不懂,于是恶补了一波。学习这些东西并不难,只是难找到学习资料。简单地搜索了一下,许多文章都是一堆公式,这谁看得懂啊。
后来找到一篇《An Introduction to the Conjugate Gradient Method Without the Agonizing Pain》,解惑了。
为什么中文没有这么良心的资料呢?英文看着费劲,于是翻译过来搬到自己的博客,以便回顾。
由于原文比较长,一共 66 66 66 页的PDF,所以这里分成几个部分来写。
目录
共轭梯度法(Conjugate Gradients)(1)
共轭梯度法(Conjugate Gradients)(2)
共轭梯度法(Conjugate Gradients)(3)
共轭梯度法(Conjugate Gradients)(4)
共轭梯度法(Conjugate Gradients)(5)
Abstract (摘要)
共轭梯度法(Conjugate Gradient Method)是求解稀疏线性方程组最棒的迭代方法。然鹅,许多教科书上面既没有插图,也没有解说,学生无法得到直观的理解。时至今日(今日指1993年,因为这份教材是1993年发表的),仍然能看到这些教材的受害者们在图书馆的角落里毫无意义地琢磨。只有少数的大佬破译了这些正常人看不懂的教材,有深刻地几何上的理解。然而,共轭梯度法只是一些简单的、优雅的思路的组合,像你一样的读者都可以毫不费力气学会。
本文介绍了二次型(quadratic forms),用于推导最速下降(Steepest Descent),共轭方向(Conjugate Directions)和共轭梯度(Conjugate Gradients)。
解释了特征向量(Eigenvectors),用于检验雅可比方法(Jacobi Method)、最速下降、共轭梯度的收敛性。
还有其它的主题,包括预处理(preconditioning)和非线性共轭梯度法(nonlinear Conjugate Gradient Method)
1. Introduction(简介)
当我决定准备学共轭梯度法(Conjugate Gradient Method, 简称 CG)的时候,读了 4 4 4 种不同的版本,恕我直言,一个都看不懂。很多都是简单地给出公式,证明了一下它的性质。没有任何直观解释,没有告诉你 CG 是怎么来的,怎么发明的。我感到沮丧,于是写下了这篇文章,希望你能从中学到丰富和优雅的算法,而不是被大量的公式困惑。
CG 是一种最常用的迭代方法,用于求解大型线性方程组,对于这种形式的问题非常有效: A x = b (1) Ax=b\tag{1} Ax=b(1) 其中:
x x x 是未知向量, b b b 是已知向量。
A A A 是已知的 方形的(square)、对称的(symmetric)、正定的(positive-definite)矩阵。
(如果你忘了什么是“正定”,不用担心,我会先给你回顾一下。)
这样的系统会出现在许多重要场景中,如求解偏微分方程(partial differential equations)的有限差分(finite difference)和有限元(finite element)法、结构分析、电路分析和你的数学作业。
像 CG 这样的迭代方法适合用稀疏(sparse)矩阵。如果 A A A 是稠密(dense)矩阵,最好的方法可能是对 A A A 进行因式分解(factor),通过反代入来求解方程。对稠密矩阵 A A A 做因式分解的耗时和迭代求解的耗时大致相同。一旦对 A A A 进行因式分解后,就可以通过多个 b b b 的值快速求解。稠密矩阵和大一点的稀疏矩阵相比,占的内存差不多。稀疏的 A A A 的三角因子通常比 A A A 本身有更多的非零元素。由于内存限制,因式分解不太行,时间开销也很大,即使是反求解步骤也可能比迭代解法要慢。另外一方面,绝大多数迭代法用稀疏矩阵都不占内存且速度快。
下面开始,我就当作你已经学过线性代数(linear algebra),对矩阵乘法(matrix multiplication)和线性无关(linear independence)等概念都很熟悉,尽管那些特征值特征向量什么的可能已经不太记得了。我会尽量清楚地讲解 CG 的概念。
2. Notation(标记)
∙ \bullet ∙ 除了一些特例,这里一般用大写字母表示矩阵(matrix),小写字母表示向量(vector),希腊字母表示标量(scalar)。
所以 A A A 是一个 n × n n\times n n×n 的矩阵, x x x 和 b b b 是向量(同时也是 n × 1 n \times 1 n×1 矩阵)。公式(1) 的完整写法:
[ A 11 A 12 … A 1 n A 21 A 22 … A 2 n ⋮ ⋱ ⋮ A n 1 A n 2 … A n n ] [ x 1 x 2 ⋮ x n ] = [ b 1 b 2 ⋮ b n ] \begin{bmatrix} A_{11} & A_{12} & \dots & A_{1n} \\[0.5em] A_{21} & A_{22} & \dots & A_{2n} \\[0.5em] \vdots & & \ddots & \vdots \\[0.5em] A_{n1} & A_{n2} & \dots & A_{nn} \\ \end{bmatrix} \begin{bmatrix} x_1 \\[0.5em] x_2 \\[0.5em] \vdots \\[0.5em] x_n \end{bmatrix} = \begin{bmatrix} b_1 \\[0.5em] b_2 \\[0.5em] \vdots \\[0.5em] b_n \end{bmatrix} ⎣⎢⎢⎢⎢⎢⎡A11A21⋮An1A12A22An2……⋱…A1nA2n⋮Ann⎦⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎡x1x2⋮xn⎦⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎡b1b2⋮bn⎦⎥⎥⎥⎥⎥⎤
∙ \bullet ∙ 两个向量的内积(inner product)写成 x T y x^{T}y xTy,可以用标量的和 ∑ i = 1 n x i y i \sum^{n}_{i=1} x_i y_i ∑i=1nxiyi 来表示。
注意这里 x T y = y T x x^T y = y^T x xTy=yTx。 如果 x x x 和 y y y 是正交(orthogonal)的,则 x T y = 0 x^T y = 0 xTy=0。
x T y = y T x = ∑ i = 1 n x i y i x T y = 0 ( 正 交 ) x^{T}y = y^T x = \sum^{n}_{i=1} x_i y_i \\[0.5em]x^T y = 0 (正交) xTy=yTx=i=1∑nxiyixTy=0(正交)
一般来说,这些运算会得到 1 × 1 1 \times 1 1×1 的矩阵。像 x T y x^T y xTy 和 x T A x x^T A x xTAx 这种,运算结果是一个标量值。
∙ \bullet ∙ 对于任意非零向量 x x x,如果下面的 公式(2) 成立,则矩阵 A A A 是正定(positive-definite)的:
x T A x > 0 (2) x^T A x > 0 \tag{2} xTAx>0(2) 这可能对你来说没什么意义,但是不要感到难过。
因为它不是一种很直观的概念,很难去想像一个正定和非正定的矩阵看起来有什么不同。
当我们看到它怎么对二次型的造成影响时,你就会对“正定”产生感觉了。
∙ \bullet ∙ 最后,还有一些基本的定义:
( A B ) T = B T A T ( A B ) − 1 = B − 1 A − 1 (AB)^T = B^T A^T \\[0.5em] (AB)^{-1} = B^{-1} A^{-1} (AB)T=BTAT(AB)−1=B−1A−1
3. The Quadratic Form(二次型)
二次型(quadratic form)简单来说是一个标量。
一个向量的二次型方程具有以下形式:
f ( x ) = 1 2 x T A x − b T x + c (3) f(x) = \frac{1}{2} x^T A x - b^T x + c \tag{3} f(x)=21xTAx−bTx+c(3)
其中 A A A 是一个矩阵, b b b 是一个向量, c c c 是一个标量常数。
如果 A A A 是对称(symmetric) 且正定(positive-definite),则 f ( x ) f(x) f(x) 的最小化问题等同于求解 A x = b Ax=b Ax=b。
本文的所有例子都基于下面的值来讲解:
A = [ 3 2 2 6 ] , b = [ 2 − 8 ] , c = 0 (4) A = \begin{bmatrix} 3 & 2 \\ 2 & 6 \end{bmatrix}, \quad b = \begin{bmatrix} 2 \\ -8 \end{bmatrix}, \quad c=0 \tag{4} A=[3226],b=[2−8],c=0(4)
可以把 (4) 代入 (3) 得到:
f ( x ) = 1 2 ⋅ [ x 1 x 2 ] [ 3 2 2 6 ] [ x 1 x 2 ] − [ 2 − 8 ] ⋅ [ x 1 x 2 ] + 0 = 1 2 ⋅ [ x 1 x 2 ] [ 3 x 1 + 2 x 2 2 x 1 + 6 x 2 ] − ( 2 x 1 − 8 x 2 ) = 1 2 ⋅ ( x 1 ( 3 x 1 + 2 x 2 ) + x 2 ( 2 x 1 + 6 x 2 ) ) − 2 x 1 + 8 x 2 = 3 2 x 1 2 + 3 x 2 2 + 2 x 1 x 2 − 2 x 1 + 8 x 2 \begin{aligned} f(x) &= \dfrac{1}{2} \cdot \begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix} 3 & 2 \\[0.5em] 2 & 6 \end{bmatrix} \begin{bmatrix} x_1 \\[0.5em] x_2 \end{bmatrix} - \begin{bmatrix} 2 & -8 \end{bmatrix} \cdot \begin{bmatrix} x_1 \\[0.5em] x_2 \end{bmatrix} + 0 \\[1.5em] &= \dfrac{1}{2} \cdot \begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix} 3x_1 + 2x_2 \\[0.5em] 2x_1 + 6x_2 \end{bmatrix} - (2x_1 - 8x_2) \\[1.5em] &= \dfrac{1}{2} \cdot {\Large(} x_1\left( 3x_1+ 2x_2 \right) + x_2 \left( 2x_1 + 6x_2\right) {\Large)} - 2x_1 + 8x_2 \\[1.5em] &= \frac{3}{2}x_1^2 + 3x_2^2 + 2x_1 x_2 -2x_1 + 8x_2 \end{aligned} f(x)=21⋅[x1x2][3226][x1x2]−[2−8]⋅[x1x2]+0=21⋅[x1x2][3x1+2x22x1+6x2]−(2x1−8x2)=21⋅(x1(3x1+2x2)+x2(2x1+6x2))−2x1+8x2=23x12+3x22+2x1x2−2x1+8x2
所以二次型其实是 n n n 个变量的二次齐次多项式。
再举一个例子,当有 3 3 3 个变量时,二次型大概像这样子: a x 1 2 + b x 2 2 + c x 3 2 + d x 1 x 2 + e x 1 x 3 + f x 2 x 3 + g ax_1^2 + bx_2^2 + cx_3^2 + dx_1 x_2 + ex_1 x_3 + fx_2 x_3 + g ax12+bx22+cx32+dx1x2+ex1x3+fx2x3+g
方程组 A x = b Ax=b Ax=b 如图(1)所示。
通常来说,方程的解 x x x 处于 n n n 维超平面相交的地方,这些相交的位置维度是 n − 1 n-1 n−1。
(直线相交于点,平面相交于线, 3 3 3 维相交于面, … \dots …)。
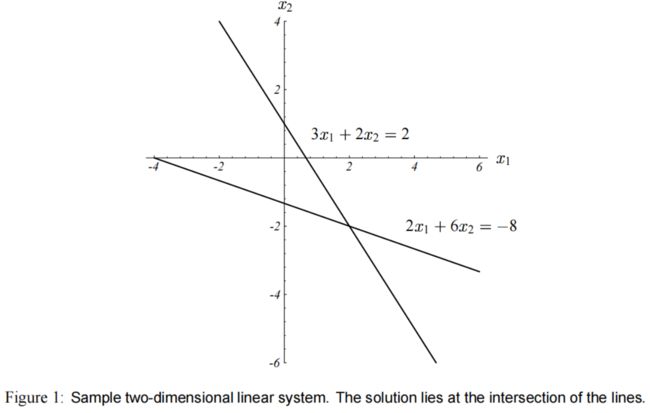
对于 A x = b Ax=b Ax=b 这个问题 ,方程的解 x = [ 2 , − 2 ] T x= [2, -2]^T x=[2,−2]T,也就是 图(1) 两条直线的交点。
对应的二次型 f ( x ) = 1 2 x T A x − b T x + c f(x) = \frac{1}{2} x^T A x - b^T x + c f(x)=21xTAx−bTx+c ,它的曲线如图(2)所示。
A x = b Ax=b Ax=b 的解是 f ( x ) f(x) f(x) 的最小值的点。
f ( x ) f(x) f(x) 的等高线(contour plot)如图(3)所示。

由于 A A A 是正定的,所以函数 f ( x ) f(x) f(x) 的形状是一个抛物碗状。
二次型的梯度(gradient)由以下式子而来:
f ′ ( x ) = [ ∂ ∂ x 1 f ( x ) ∂ ∂ x 2 f ( x ) ⋮ ∂ ∂ x n f ( x ) ] (5) f'(x)= \begin{bmatrix} \dfrac{\partial}{\partial x_1} f(x) \\[1em] \dfrac{\partial}{\partial x_2} f(x) \\[1em] \vdots \\[1em] \dfrac{\partial}{\partial x_n} f(x) \end{bmatrix} \tag{5} f′(x)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x)⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤(5)
梯度是一个向量场,对于每一个点 x x x,它指向 f ( x ) f(x) f(x) 增大得最快的方向。
图(4) 展示了 式子(3) 的梯度,其中具体的参数如 式子(4) 所示。

在碗状的底部,梯度为 0 0 0。因此令 f ′ ( x ) = 0 f'(x)=0 f′(x)=0 可以最小化 f ( x ) f(x) f(x)。
应用 式子(5) 来求导,可以得到: f ′ ( x ) = 1 2 A T x + 1 2 A x − b (6) f'(x) = \dfrac{1}{2} A^T x + \dfrac{1}{2}Ax - b \tag{6} f′(x)=21ATx+21Ax−b(6) 如果 A A A 是对称的,式子会被化简为 f ′ ( x ) = A x − b (7) f'(x) = Ax-b\tag{7} f′(x)=Ax−b(7)因为此时 A T = A A^T = A AT=A。
梯度设为 0 0 0,就能得到 式子(1),也就是我们要求解的线性方程组。
A x = b Ax=b Ax=b 的解就是 f ( x ) f(x) f(x) 的关键点。如果 A A A 是正定且对称的,则这个解能使 f ( x ) f(x) f(x) 最小化。
所以, A x = b Ax=b Ax=b 的解 x x x 能使 f ( x ) f(x) f(x) 最小。
如果 A A A 不是 正定 的,从 式子(6) 可知用 CG 可以求解方程组 1 2 ( A T + A ) x = b \dfrac{1}{2} (A^T + A)x=b 21(AT+A)x=b 。 ( \Large( ( 因为 1 2 ( A T + A ) \dfrac{1}{2} (A^T + A) 21(AT+A) 是对称的 ) \Large) )
【附录C1】
假设 A A A 是对称的。
令 x x x 满足 A x = b Ax=b Ax=b,并且能使二次型(式子(3)) 最小;
令 e e e 为误差项;
则:
f ( x + e ) = 1 2 ( x + e ) T A ( x + e ) − b T ( x + e ) + c = 1 2 x T A x + e T A x + 1 2 e T A e − b T x − b T e + c = 1 2 x T A x + e T b + 1 2 e T A e − b T x − b T e + c = 1 2 x T A x − b T x + c + e T b + 1 2 e T A e − b T e = f ( x ) + 1 2 e T A e \begin{aligned} f(x+e) &= \frac{1}{2}(x+e)^{T} A (x+e) - b^{T} (x+e) + c \\[0.5em] &= \frac{1}{2}x^{T}Ax + e^{T}Ax + \frac{1}{2}e^TAe - b^T x - b^T e + c \\[0.5em] &= \frac{1}{2}x^{T}Ax + e^{T}b + \frac{1}{2}e^TAe - b^T x - b^T e + c \\[0.5em] &= \frac{1}{2}x^{T}Ax - b^T x + c + e^{T}b + \frac{1}{2}e^TAe - b^T e \\[0.5em] &= f(x) + \frac{1}{2}e^T A e \end{aligned} f(x+e)=21(x+e)TA(x+e)−bT(x+e)+c=21xTAx+eTAx+21eTAe−bTx−bTe+c=21xTAx+eTb+21eTAe−bTx−bTe+c=21xTAx−bTx+c+eTb+21eTAe−bTe=f(x)+21eTAe
如果 A A A 是正定的,则对于任意 e ≠ 0 e\neq0 e=0 有 1 2 e T A e > 0 \dfrac{1}{2}e^T A e >0 21eTAe>0,因此 x x x 能最小化 f f f。
为什么 对称 且 正定 的矩阵有这样的性质? 可以考虑函数 f f f 上任意一点 p p p ,和它的解 x = A − 1 b x=A^{-1} b x=A−1b 之间的关系。
如果 A 是对称的(无论正定与否),由 式子(3) 和 附录C1,令 e = p − x e = p- x e=p−x 可得: f ( p ) = f ( x ) + 1 2 ( p − x ) T A ( p − x ) (8) f(p) = f(x) + \dfrac{1}{2} (p-x) ^T A (p-x) \tag{8} f(p)=f(x)+21(p−x)TA(p−x)(8)
如果此时 A A A 又能正定的话,由 式子(2) 得知对于任意 p ≠ x p \neq x p=x 有 1 2 ( p − x ) T A ( p − x ) > 0 \dfrac{1}{2} (p-x) ^T A (p-x) >0 21(p−x)TA(p−x)>0,所以一定有 f ( p ) > f ( x ) f(p) > f(x) f(p)>f(x),所以 x x x 是全局最小。
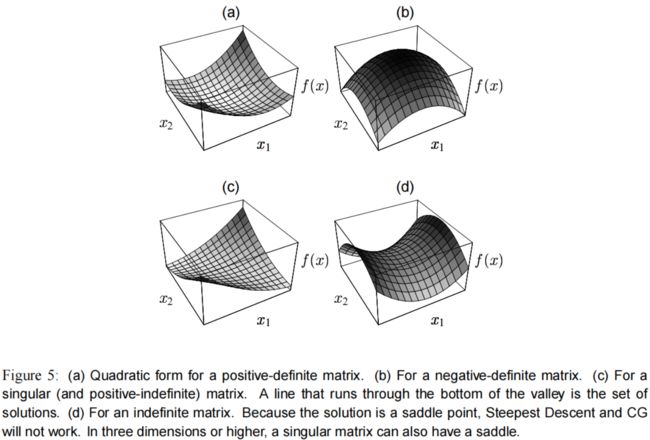
正定(positive-definite) 矩阵到底意味着什么?最直观的感受就是, f ( x ) f(x) f(x) 的图形是一个碗状。
如果 A A A 是 非正定 的,那么有以下几种可能:
∙ \bullet ∙ 负定(negative-definite)矩阵。相当于对正定取反,如 图(5)b。
∙ \bullet ∙ 奇异(singular)矩阵。这种情况下解不是唯一的,如 图(5)c。解集是一条直线或者超平面,在那里 f f f 具有相同的值。
∙ \bullet ∙ 如果矩阵 A A A 不属于以上情况,那么 x x x 是一个鞍点(saddle point),最速下降法 和 共轭梯度法 都将失效。
式(3) 中的 b b b 和 c c c 决定碗状的极小值在哪里,但不影响抛物面的形状。
为什么要把线性方程组弄得这么麻烦?
因为下面要讲的 最速下降法 和 共轭梯度法 ,需要基于 图(2) 这种最小化问题,才能进行直观的理解。
而不是研究 图(1) 这种超平面的相交的问题。
(即,把问题转成求 极小值,而不是 找交点)
4. The Method of Steepest Descent(最速下降法)
或者叫最陡下降。
我们会从任意点 x ( 0 ) x_{(0)} x(0) 开始,滑到碗状面的底部。我们会走到 x ( 1 ) , x ( 2 ) , … x_{(1)}, x_{(2)},\dots x(1),x(2),…,直到足够接近方程的解 x x x。
每走一步的时候,我们要选择 f f f 下降最快的方向,也就是 f ′ ( x ( i ) ) f'(x_{(i)}) f′(x(i)) 的反方向。
根据 式子(7),这个方向就是 − f ′ ( x ( i ) ) = b − A x ( i ) -f'(x_{(i)}) = b- Ax_{(i)} −f′(x(i))=b−Ax(i)。
这里再引入一些定义:
∙ \bullet ∙ 误差(error) e ( i ) = x ( i ) − x e_{(i)} = x_{(i)} - x e(i)=x(i)−x。
表示与 解 有多远。(这个解叫做 精确解(exact solution))
∙ \bullet ∙ 残差(residual) r ( i ) = b − A x ( i ) r_{(i)} = b - Ax_{(i)} r(i)=b−Ax(i)。
表示与正确值 b b b 有多远。
容易发现,残差 可以由 误差 变换得来: ∙ \bullet ∙ r i = − A e ( i ) r_{i} = -Ae_{(i)} ri=−Ae(i)。
误差反映的是变量的层面,残差描述的是函数值的层面,所以通过 A A A 从变量空间转换到函数值的空间。
更重要的是: r i = − f ′ ( x ( i ) ) r_{i} = - f'(x_{(i)}) ri=−f′(x(i)) 你可以认为 残差 r i r_i ri 是 最陡下降的方向 (原函数的导数的反方向)。
(这里也很容易理解,因为向量是有方向的,它反映了函数值和真实值之间的距离,同时方向也指向真实值)
对于非线性问题,我们用的就是这一种定义。
所以每当你看到残差 r r r,请记住它是最速下降的方向。
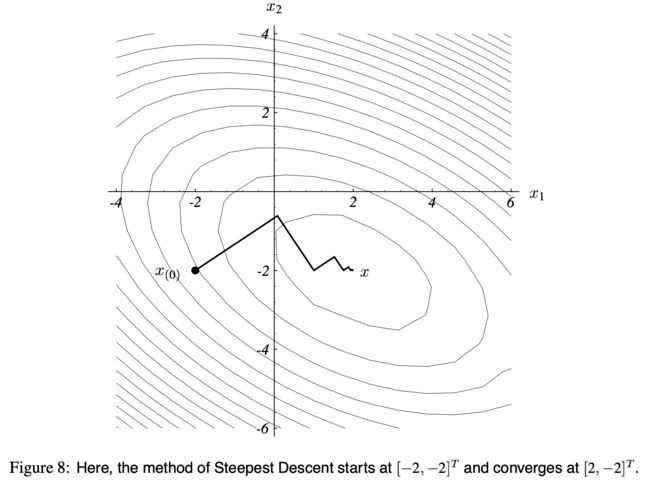
假设我们从 x ( 0 ) x_{(0)} x(0) 开始, x ( 0 ) = [ − 2 , − 2 ] T x_{(0)} = [-2, -2]^T x(0)=[−2,−2]T。
第 1 1 1 步,我们沿着最陡方向走 1 1 1 步,落在 图(6)a 中的实线的某处。
换句话来讲,我们会选择这样一个点: x ( 1 ) = x ( 0 ) + α r ( 0 ) (9) x_{(1)} = x_{(0)}+ \alpha r_{(0)} \tag{9} x(1)=x(0)+αr(0)(9)问题是,这一步要迈多大呢?(可以把 α \alpha α 看做学习率)
线搜索(line search)是这样一种过程:沿着一条线选择一个 α \alpha α,使得 f f f 最小化。
图(6)b :竖直平面和碗状曲面相交于一条横切线,我们要的点在这条线上。
图(6)c :是这条横切线(从这个视角来看是抛物线)。那么在抛物线的底部, α \alpha α 的值是多少呢?
由基本推导有,当方向导数(directional derivative) d d α f ( x ( 1 ) ) = 0 \dfrac{d}{d\alpha} f(x_{(1)})=0 dαdf(x(1))=0 时, α \alpha α 能使 f f f 最小。
根据链式求导法则: d d α f ( x ( 1 ) ) = f ′ ( x ( 1 ) ) T d d α x ( 1 ) = f ′ ( x ( 1 ) ) T r ( 0 ) \dfrac{d}{d\alpha} f(x_{(1)})=f'(x_{(1)})^T \dfrac{d}{d\alpha}x_{(1)} =f'(x_{(1)})^T r_{(0)} dαdf(x(1))=f′(x(1))Tdαdx(1)=f′(x(1))Tr(0)。
(关于求导的方法可以看[这里]或者[这里])
为什么 d d α x ( 1 ) = r ( 0 ) \dfrac{d}{d\alpha}x_{(1)} = r_{(0)} dαdx(1)=r(0),因为根据 式子(9) 有 x ( 1 ) = x ( 0 ) + α r ( 0 ) x_{(1)} = x_{(0)}+ \alpha r_{(0)} x(1)=x(0)+αr(0),把 x ( 1 ) x_{(1)} x(1) 代进去。
令这条式子为 0 0 0,我们会发现这个 α \alpha α 应该使 r ( 0 ) r_{(0)} r(0) 和 f ′ ( x ( 1 ) ) f'(x_{(1)}) f′(x(1)) 正交。见 图(6)d。
所以,为什么我们期望这些向量正交,这就是最直观的原因 。☝↑☝
图(7) 展示了搜索线上不同点的梯度向量。虚线是这些梯度向量在搜索线上的投影。这些虚线的大小等同于 图(6)c 中抛物线上每个点的斜率。这些投影表示当你在这条搜索线上移动时, f f f 的增长率。当投影为 0 0 0 时, f f f 最小,此时的 梯度 和 搜索线 正交。
为了确定 α \alpha α,由于又有 f ′ ( x ( 1 ) ) = − r ( 1 ) f'(x_{(1)}) = -r_{(1)} f′(x(1))=−r(1),于是有:
r ( 1 ) T r ( 0 ) = 0 ( b − A x ( 1 ) ) T r ( 0 ) = 0 ( b − A ( x ( 0 ) + α r ( 0 ) ) ) T r ( 0 ) = 0 ( b − A x ( 0 ) ) T r ( 0 ) − α ( A r ( 0 ) ) T r ( 0 ) = 0 ( b − A x ( 0 ) ) T r ( 0 ) = α ( A r ( 0 ) ) T r ( 0 ) r ( 0 ) T r ( 0 ) = α r ( 0 ) T ( A r ( 0 ) ) α = r ( 0 ) T r ( 0 ) r ( 0 ) T A r ( 0 ) \begin{aligned} r^T_{(1)} r_{(0)} & =0 \\ (b- Ax_{(1)})^T r_{(0)} &= 0 \\ {\large(} b - A(x_{(0)} + \alpha r_{(0)}) {\large)}^T r_{(0)} &= 0 \\ (b-Ax_{(0)})^T r_{(0)} - \alpha (Ar_{(0)})^Tr_{(0)} &= 0 \\ (b-Ax_{(0)})^T r_{(0)} &= \alpha (Ar_{(0)})^T r_{(0)} \\ r^T_{(0)} r_{(0)} &= \alpha r^T_{(0)} (Ar_{(0)}) \\ \alpha &= \dfrac{r^T_{(0)} r_{(0)}}{r^T_{(0)} A r_{(0)}} \end{aligned} r(1)Tr(0)(b−Ax(1))Tr(0)(b−A(x(0)+αr(0)))Tr(0)(b−Ax(0))Tr(0)−α(Ar(0))Tr(0)(b−Ax(0))Tr(0)r(0)Tr(0)α=0=0=0=0=α(Ar(0))Tr(0)=αr(0)T(Ar(0))=r(0)TAr(0)r(0)Tr(0)
结合起来,最陡下降法(Steepest Descent)就是:
r ( i ) = b − A x ( i ) , (10) r_{(i)} = b - A x_{(i)} ,\tag{10} r(i)=b−Ax(i),(10) α ( i ) = r ( i ) T r ( i ) r ( i ) T A r ( i ) , (11) \alpha_{(i)} = \frac{r^T_{(i)}r_{(i)}}{r^T_{(i)}Ar_{(i)}},\tag{11} α(i)=r(i)TAr(i)r(i)Tr(i),(11) x ( i + 1 ) = x ( i ) + α ( i ) r ( i ) . (12) x_{(i+1)} = x_{(i)} + \alpha_{(i)}r_{(i)}. \tag{12} x(i+1)=x(i)+α(i)r(i).(12)
如 图(8) 所示,一直迭代,直到收敛。
由于每一次的梯度都和上一次的正交,所以这个路径呈“之”字型。
上面的算法,要在每轮迭代中做两次矩阵-向量的乘法,不过好在有一个可以被消掉。
在 式子(12) 两边同时左乘 − A -A −A,再加 b b b,得:
r ( i + 1 ) = r ( i ) − α ( i ) A r ( i ) (13) r_{(i+1)} = r_{(i)}-\alpha_{(i)}Ar_{(i)} \tag{13} r(i+1)=r(i)−α(i)Ar(i)(13)
尽管 式子(10) 仍然要算一次 r ( 0 ) r_{(0)} r(0),不过之后每轮迭代都可以用 式子(13) 了。
式子(11) 和 式子(13) 中的乘法 A r Ar Ar 只需要被计算一次。
这个迭代的缺点是, 公式(13) 生成的序列没有从 x ( i ) x_{(i)} x(i) 的值里得到任何回馈。因此对浮点舍入造成的累积误差会使 x ( i ) x_{(i)} x(i) 收敛至 x x x 附近的点,而无法真正地收敛到 x x x。这种影响可以通过周期性地使用 式子(10) 来重新计算正确的残差来避免。
在分析最陡下降的收敛性之前,还要先讲一下特征向量(eigenvectors)的知识,确保你对特征向量有深刻的理解。
5. Thinking with Eigenvectors and Eigenvalues(特征向量和特征值的思考)
上完线性代数课程后,我对特征向量和特征值了如指掌。如果你的老师和我一样,你会记得自己解决了一些关于特征值的问题,但你从来没有真正理解过它们。不幸的是,如果没有对它们的直观理解,CG 也没有意义。如果你已经很有天赋,可以跳过这一节。
特征向量(eigenvectors)主要用来当做分析工具,最陡下降法和共轭梯度法不用计算特征向量的特征值。
5.1 Eigen do it if I try
矩阵 B B B 的特征向量 v v v 是一个非零的向量,用 B B B 乘以它的时候,不会发生旋转(只可能掉头)。
特征向量 v v v 的长度可能会变,或者反方向,但不会转。
也就是说,存在一些标量常数 λ \lambda λ 使得 B v = λ v Bv=\lambda v Bv=λv。
λ \lambda λ 就是 B B B 的特征值(eigenvalue)。
为什么要讲这个,因为迭代法通常会用 B B B 一次又一次地乘上特征向量,而这时只会发生两种情况:
(1) 如果特征值 ∣ λ ∣ < 1 |\lambda| < 1 ∣λ∣<1,随着 i i i 的迭代, B i v = λ i v B^iv = \lambda^i v Biv=λiv 会消失。(如 图(9))

(2) 如果特征值 ∣ λ ∣ > 1 |\lambda| > 1 ∣λ∣>1,随着 i i i 的迭代, B i v B^iv Biv 会增大到无穷。(如 图(10))
如果 B B B 是对称的(然而一般都不是),一般会存在一组 n n n 个线性无关的特征向量: v 1 , v 2 , … , v n v_1, v_2, \dots, v_n v1,v2,…,vn 。
这组向量不是唯一的,因为可以用任意的非零常数对它们缩放。
每个特征向量都有对应的特征值: λ 1 , λ 2 , … , λ n \lambda_1, \lambda_2, \dots, \lambda_n λ1,λ2,…,λn。
对于确定的矩阵,特征值是唯一的。
特征值可能彼此相等,也可能不相等,例如单位矩阵 I I I 的特征值都是 1 1 1,所有非零向量都是 I I I 的特征向量。
如果 B B B 乘以一个向量,而该向量不是特征向量呢?
在理解线性代数时有一个非常重要的技巧:把该向量拆成 多个向量的和 ,这些多个向量特性是已知的。
考虑一组特征向量 { v i } \{v_i\} {vi},构成 n n n 维空间 R n \mathbb{R}^n Rn 的基(因为对称矩阵 B B B 有 n n n 个线性无关的特征向量)。
在该空间中其它任意的 n n n 维向量都可以用 { v i } \{v_i\} {vi} 的线性组合来表示。
由于矩阵-向量的乘法满足 分配律,所以可以分别检查 B B B 对每个特征向量的影响。
在 图(11) 中,向量 x x x 被表示为特征向量 v 1 v_1 v1 和 v 2 v_2 v2 的和。
用 B B B 乘以 x x x,等价于分别乘以 v 1 v_1 v1 和 v 2 v_2 v2 再加起来。
在迭代过程中有 B i x = B i v 1 + B i v 2 = λ 1 i v 1 + λ 2 i v 2 B^i x = B^i v_1 + B^i v_2 = \lambda_1^i v_1 + \lambda_2^i v_2 Bix=Biv1+Biv2=λ1iv1+λ2iv2。
如果特征值都小于 1 1 1, B i x B^ix Bix 会收敛至 0 0 0,因为迭代地乘 B B B 后,组成 x x x 的特征向量都趋于 0 0 0 了。
如果其中一个特征值大于 1 1 1, x x x 将发散至无穷。
这也是为什么做数值分析的很重视一个矩阵的光谱半径(spectral radius): ρ ( B ) = max ∣ λ i ∣ , λ i is an eigenvalue of B \rho(B) = \max | \lambda_i|, \qquad \lambda_i \text{ is an eigenvalue of } B ρ(B)=max∣λi∣,λi is an eigenvalue of B
如果我们希望 x x x 快速收敛到 0 0 0, ρ ( B ) \rho(B) ρ(B) 应当小于 1 1 1,越小越好。
值得一提的是,存在一类非对称矩阵,不具备完整的 n n n 个线性无关特征向量。
这类矩阵被称为缺陷矩阵(defective)。关于它的细节很难在本文讲清楚,不过可以通过广义特征向量(generalized eigenvectors)和 广义特征值(generalized eigenvalues)来分析缺陷矩阵的性质。 B i x B^ix Bix 趋于 0 0 0 的条件是:当且仅当所有广义特征值都于 1 1 1。但这个证明起来很难。
下面是一个有用的事实:正定矩阵的特征值都是正数。
可以用特征值的定义来证明: B v = λ v v T B v = λ v T v \begin{aligned} Bv &= \lambda v \\ v^T Bv &= \lambda v^Tv\end{aligned} BvvTBv=λv=λvTv
根据正定矩阵的定义,对于非零向量 v v v,有 v T B v v^TBv vTBv 是正数,而 v T v = v 1 2 + v 2 2 + ⋯ + v n 2 > 0 v^Tv=v_1^2 + v_2^2 + \dots + v_n^2 > 0 vTv=v12+v22+⋯+vn2>0,所以 λ \lambda λ 必须大于为正。
5.2 Jacobi iterations(雅克比迭代)
当然,总是收敛到 0 0 0 的过程不会帮助你吸引到朋友。
考虑一个更有用的过程:用雅克比(Jacobi Method)方法求解 A x = b Ax=b Ax=b 。
矩阵 A A A 被拆成两部分:
(1) D D D,对角线上的元素与 A A A 的对角线相同,其余部分为 0 0 0。
(2) E E E,对角线上的元素为 0 0 0,其余部分与 A A A 相同。
于是 A = D + E A=D+E A=D+E。
我们推导出雅克比法:
A x = b D x = − E x + b x = − D − 1 E x + D − 1 b x = B x + z (14) \begin{aligned} Ax &= b \\ Dx &= -Ex+b \\ x &= -D^{-1}Ex + D^{-1}b \\ x &= Bx+z \end{aligned} \tag{14} AxDxxx=b=−Ex+b=−D−1Ex+D−1b=Bx+z(14)
由于 D D D 是对角矩阵,很容易求逆。
可以通过下面的递归式,把 式子(14) 的恒等式转为迭代法: x ( i + 1 ) = B x ( i ) + z (15) x_{(i+1)} = Bx_{(i)} + z \tag{15} x(i+1)=Bx(i)+z(15)
给定起始向量 x ( 0 ) x_{(0)} x(0),这条公式生成了一序列的向量。我们希望每个连续的向量都比最后一个更接近解 x x x。
x x x 称为 式子(15) 的驻点(stationary point)。因为,如果 x ( i ) = x x_{(i)} = x x(i)=x,则 x ( i + 1 ) x_{(i+1)} x(i+1) 总是等于 x x x。(也就是到达 x x x 之后,再迭代也不动了)
是的,这个推导可能对你来说过于直接。
除了 式子(14) 以外,我们其实可以为 x x x 形成任意数量的恒等式。
事实上,简单地把 A A A 分成不同的东西,即选择不同的 D D D 和 E E E,我们可以推导出高斯-赛德尔( Gauss-Seidel method)方法,或者其变种:SOR( Successive Over-Relaxation)。我们希望的是,所选择的矩阵使 B B B 具有小的光谱半径。所以为了简单起见,这里直接选择了雅克比切法。
假设我们从任意的 x ( 0 ) x_{(0)} x(0) 出发。对于每次迭代,用 B B B 乘以这个向量,然后加上 z z z。到底每次迭代在做什么呢?
同样地,我们可以把一个向量看成是多个已知向量的和。
把每次迭代 x ( i ) x_{(i)} x(i) 当做是精确解 x x x 和误差项 e ( i ) e_{(i)} e(i) 的和。于是 式子(15) 就变成了:
x ( i + 1 ) = B x ( i ) + z = B ( x + e ( i ) ) + z = B x + z + B e ( i ) = x + B e ( i ) (by Eauation 14) \begin{aligned} x_{(i+1)} &= Bx_{(i)} + z \\ &= B(x+ e_{(i)}) + z \\ &= Bx + z + Be_{(i)} \\ &= x + Be_{(i)} \qquad \text{(by Eauation 14)} \end{aligned} x(i+1)=Bx(i)+z=B(x+e(i))+z=Bx+z+Be(i)=x+Be(i)(by Eauation 14) ∴ e ( i + 1 ) = B e ( i ) (16) \therefore e_{(i+1)} = Be_{(i)} \tag{16} ∴e(i+1)=Be(i)(16)
每次迭代都不影响 x ( i ) x_{(i)} x(i) 的 “正确部分”(因为 x x x 是一个驻点);但每次迭代影响误差项。
显然,由 式子(16) 得知,如果 ρ ( B ) < 1 \rho(B) < 1 ρ(B)<1,则随着 i i i 的增大, e ( i ) e_{(i)} e(i) 将趋于 0 0 0。
因此,初始向量 x 0 x_0 x0 不会影响必将出现的结果!
当然, x ( 0 ) x_{(0)} x(0) 的选择会影响迭代次数。然而,这种影响远远小于光谱半径 ρ ( B ) \rho(B) ρ(B) 的影响,是它决定了收敛的速度。
假设 v j v_j vj 是 B B B 的特征向量,对应的特征值是最大的(即 ρ ( B ) = λ j \rho(B) = \lambda_j ρ(B)=λj)。
如果初始误差 e ( 0 ) e_{(0)} e(0) 用特征向量的线性组合来表示,它的成分中包含 v j v_j vj 的方向,这部分将会是收敛得最慢的。(因为 v j v_j vj 对应的特征值是 λ j \lambda_j λj, λ j \lambda_j λj 是所有特征值里面最大的,所以 v j v_j vj 缩小的最慢,所以这个方向收敛得很慢)
B B B 通常都不是对称的(就算 A A A 是对称的),还可能是缺陷矩阵。然而,雅克比方法的收敛速度很大程度上取决于 ρ ( B ) \rho(B) ρ(B),而 B B B 又是由 A A A 决定的。雅克比方法不能对所有的 A A A 收敛,即使是正定的 A A A。
5.3 A Concrete Example(一个具体例子)
为了证明这些想法,我来求解由 式子(4) 指定的实例。
首先,我们需要求解特征向量和特征值。
根据定义,对于具有特征值 λ \lambda λ 的特征向量 v v v,有: A v = λ v = λ I v ( λ I − A ) v = 0 Av =\lambda v = \lambda I v \\[0.5em] (\lambda I - A) v = 0 Av=λv=λIv(λI−A)v=0
由于特征向量非零,则 λ I − A \lambda I - A λI−A 一定是奇异矩阵,所以: det ( λ I − A ) = 0 \det(\lambda I - A) = 0 det(λI−A)=0
λ I − A \lambda I - A λI−A 的行列式称为特征多项式(characteristic polynomial),是 λ \lambda λ 的 n n n 次多项式,其平方项都是特征值。
代入 式子(4) 的值,则 A A A 的特征多项式为: det [ λ − 3 − 2 − 2 λ − 6 ] = λ 2 − 9 λ + 14 = ( λ − 7 ) ( λ − 2 ) \det \begin{bmatrix} \lambda - 3 & -2 \\ -2 & \lambda - 6 \end{bmatrix} = \lambda^2 - 9\lambda + 14 = (\lambda -7)(\lambda - 2) det[λ−3−2−2λ−6]=λ2−9λ+14=(λ−7)(λ−2)
因此特征值为 λ 1 = 7 \lambda_1 = 7 λ1=7, λ 2 = 2 \lambda_2 = 2 λ2=2。(有两个特征向量)
第 1 1 1 个特征向量:
为了找到到关于 λ 1 \lambda_1 λ1 的特征向量: ( λ 1 I − A ) v = [ 4 − 2 − 2 1 ] [ v 1 v 2 ] = 0 ∴ 4 v 1 − 2 v 2 = 0 (\lambda_1 I - A)v = \begin{bmatrix} 4 & -2 \\ -2 & 1 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = 0 \\[1.5em] \therefore 4v_1 - 2v_2 = 0 (λ1I−A)v=[4−2−21][v1v2]=0∴4v1−2v2=0
4 v 1 − 2 v 2 = 0 4v_1 - 2v_2 = 0 4v1−2v2=0 的解就是一个特征向量: v = [ 1 , 2 ] T v=[1,2]^T v=[1,2]T。
即 λ 1 \lambda_1 λ1 的特征向量为 v ( 1 ) = [ 1 , 2 ] T \pmb{v}_{(1)} =[1,2]^T vvv(1)=[1,2]T
第 2 2 2 个特征向量:
同样地,可以找到 λ 2 \lambda_2 λ2 的特征向量为 v ( 2 ) = [ − 2 , 1 ] T \pmb{v}_{(2)} =[-2,1]^T vvv(2)=[−2,1]T
在 图(12) 中,我们可以看到特征向量和椭圆的轴一致,特征值较大的那个特征向量对应更陡的斜坡(slope)。
(负的特征值表示 f f f 沿着该轴减小,如 图(5)b 和 图(5)d )
现在再来看实际中的雅克比方法。同样采用 式子(4) 中的数值,我们有:
x ( i + 1 ) = − [ 1 3 0 0 1 6 ] [ 0 2 2 0 ] x ( i ) + [ 1 3 0 0 1 6 ] [ 2 − 8 ] = [ 0 − 2 3 − 1 3 0 ] x ( i ) + [ 2 3 − 4 3 ] \begin{aligned} x_{(i+1)} &= - \begin{bmatrix} \dfrac{1}{3} & 0 \\[0.5em] 0 &\dfrac{1}{6}\end{bmatrix} \begin{bmatrix} 0 & 2 \\[0.5em] 2 & 0 \end{bmatrix} x_{(i)} + \begin{bmatrix} \dfrac{1}{3} & 0 \\[0.5em] 0 &\dfrac{1}{6}\end{bmatrix} \begin{bmatrix} 2 \\[0.5em] - 8 \end{bmatrix} \\[2em] &= \begin{bmatrix} 0 & -\dfrac{2}{3} \\[0.5em] - \dfrac{1}{3} & 0 \end{bmatrix} x_{(i)} + \begin{bmatrix} \dfrac{2}{3} \\[1.5em] -\dfrac{4}{3}\end{bmatrix} \end{aligned} x(i+1)=−⎣⎢⎡310061⎦⎥⎤[0220]x(i)+⎣⎢⎡310061⎦⎥⎤[2−8]=⎣⎢⎡0−31−320⎦⎥⎤x(i)+⎣⎢⎢⎡32−34⎦⎥⎥⎤
所以矩阵 B = [ 0 − 2 3 − 1 3 0 ] B = \begin{bmatrix} 0 & -\dfrac{2}{3} \\[0.5em] - \dfrac{1}{3} & 0 \end{bmatrix} B=⎣⎢⎡0−31−320⎦⎥⎤,求解 B B B 的特征值特征向量:
有对应于特征值 − 2 3 \dfrac{-\sqrt{2}}{3} 3−2 的特征向量 [ 2 , 1 ] T [\sqrt{2}, 1]^T [2,1]T,对应于特征值 2 3 \dfrac{\sqrt{2}}{3} 32 的特征向量 [ − 2 , 1 ] T [-\sqrt{2}, 1]^T [−2,1]T。
这两个特征向量如 图(13)a 所示。
注意, B B B 的特征向量与 A A A 的特征向量不重合,与碗状面的轴也无关。
误差项 e e e 表示为 B B B 的特征向量的线性组合。而两个特征向量都小于 1 1 1,并且有一个是负的,所以迭代 B e ( i ) Be_{(i)} Be(i) 会使特征向量收敛到 0 0 0,同时其中一个特征向量的方向不断地反转,如 图(13)的c,d,e 所示。
误差项 e ( i ) e_{(i)} e(i) 越来越小,则 x ( i ) x_{(i)} x(i) 收敛于 x x x。
图(13)b 展示了雅克比方法的收敛情况。