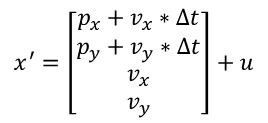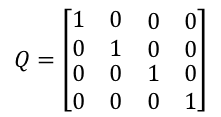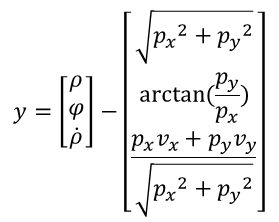扩展卡尔曼滤波

前言

《无人驾驶技术入门（十三）| 手把手教你写卡尔曼滤波器》以一个匀速运动小车的模型为例，让读者从感性上认识了卡尔曼滤波器的基本原理，它包含预测（Prediction）和测量值更新（Measurement update）两大过程。预测和测量值更新的交替执行，实现了卡尔曼滤波在状态估计中的闭环。

随后，我从理性分析的角度，以无人驾驶中激光雷达测量障碍物位置的数据为例，结合卡尔曼滤波所用到的公式，使用C++和矩阵运算库Eigen一步步实现了卡尔曼滤波器预测和测量值更新这两大过程的代码。

在本次分享中，我将以优达学城（Udacity）无人驾驶工程师学位中提供的传感器融合项目为例，介绍如何利用扩展卡尔曼滤波解决跟踪毫米波雷达目标的问题。由于本次内容为卡尔曼滤波器的进阶内容，推荐读者先阅读《无人驾驶技术入门（十三）| 手把手教你写卡尔曼滤波器》，了解预测和测量值更新这两个步骤所使用到的公式及其含义，再看此篇。

---

正文

毫米波雷达的数据

毫米波雷达观察世界的方式与激光雷达有所不同。激光雷达测量的原理是光的直线传播，因此在测量时能直接获得障碍物在笛卡尔坐标系下x方向、y方向和z方向上的距离；而毫米波雷达的原理是多普勒效应，它所测量的数据都是在极坐标系下的。

如下图所示，毫米波雷达能够测量障碍物在极坐标下离雷达的距离ρ、方向角ϕ以及距离的变化率（径向速度）ρ'，如下图所示。

图片出处：优达学城（Udacity）无人驾驶工程师学位

 

毫米波雷达的测量原理及更为详细的数据介绍可参看《无人驾驶技术入门（七）| 量产必备的毫米波雷达》。

扩展卡尔曼滤波器理论

我们再次祭出卡尔曼老先生给我们留下的宝贵财富，即状态估计时预测和测量值更新时所用到的7个公式，如下图所示。扩展卡尔曼滤波的理论和编程依旧需要使用到这些公式，相比于原生的卡尔曼滤波，只在个别地方有所不同。

图片出处：优达学城（Udacity）无人驾驶工程师学位

 

完成扩展卡尔曼滤波器C++代码的过程，实际上就是结合上面的公式，一步步完成初始化、预测、观测的过程。由于公式中涉及大量的矩阵转置和求逆运算，我们使用开源的矩阵运算库Eigen辅助我们代码的编写。

代码：初始化（Initialization）

扩展卡尔曼滤波的初始化，需要将各个变量进行设置，对于不同的运动模型，状态向量是不一样的。为了保证代码对不同状态向量的兼容性，我们使用Eigen库中非定长的数据结构。

如下所示，我们新建了一个ExtendedKalmanFilter类，定义了一个叫做x_的状态向量（state vector）。代码中的VerctorXd表示X维的列向量，元素的数据类型为double。

 

初始化扩展卡尔曼滤波器时需要输入一个初始的状态量x_in，用以表示障碍物最初的位置和速度信息，一般直接使用第一次的测量结果。

 

代码：预测（Prediction）

完成初始化后，我们开始写Prediction部分的代码。首先是公式

这里的x为状态向量，通过左乘一个矩阵F，再加上外部的影响u，得到预测的状态向量x'。这里的F被称作状态转移矩阵（state transistion matrix）。以2维的匀速运动为例，这里的x为

根据中学物理课本中的公式s1 = s0 + vt，经过时间△t后的预测状态向量应该是

对于二维的匀速运动模型，加速度为0，并不会对预测后的状态造成影响，因此

如果换成加速或减速运动模型，可以引入加速度ax和ay，根据s1 = s0 + vt + at^2/2这里的u会变成：

作为入门课程，这里不讨论太复杂的模型，因此公式

最终将写成

再看预测模块的第二个公式

该公式中P表示系统的不确定程度，这个不确定程度，在卡尔曼滤波器初始化时会很大，随着越来越多的数据注入滤波器中，不确定程度会变小，P的专业术语叫状态协方差矩阵（state covariance matrix）；这里的Q表示过程噪声（process covariance matrix），即无法用x'=Fx+u表示的噪声，比如车辆运动时突然到了上坡，这个影响是无法用之前的状态转移方程估计的。

毫米波雷达测量障碍物在径向上的位置和速度相对准确，不确定度较低，因此可以对状态协方差矩阵P进行如下初始化：

由于Q对整个系统存在影响，但又不能太确定对系统的影响有多大。对于简单的模型来说，这里可以直接使用单位矩阵或空值进行计算，即

根据以上内容和公式

我们就可以写出预测模块的代码了

实际编程时x'及P'不需要申请新的内存去存储，使用原有的x和P代替即可。

代码：观测（Measurement）

观测的第一个公式是

这个公式的目的是计算观测到的观测值z与预测值x'之间差值y。

前面提到过毫米波雷达观测值z的数据特性，如下图所示：

图片出处：优达学城（Udacity）无人驾驶工程师学位

 

由图可知观测值z的数据维度为3×1，为了能够实现矩阵运算，y和Hx'的数据维度也都为3×1。

使用基本的数学运算可以完成预测值x'从笛卡尔坐标系到极坐标系的坐标转换，求得Hx'，再与观测值z进行计算。需要注意的是，在计算差值y的这一步中，我们通过坐标转换的方式避开了未知的旋转矩阵H的计算，直接得到了Hx’的值。

为了简化表达，我们用px，py以及vx和vy表示预测后的位置及速度，如下所示：

其中测量值z和预测后的位置x'都是已知量，因此我们很容易计算得到观测与预测的差值y。

毫米波雷达在转换时涉及到笛卡尔坐标系和极坐标系的位置、速度转换，这个转化过程是非线性的。因而在处理类似毫米波雷达这种非线性的模型时，习惯于将计算差值y的公式写成如下，以作线性和非线性模型的区分。

对应上面的式子，这里的h(x')为：

再看卡尔曼滤波器接下来的两个公式

这两个公式求的是卡尔曼滤波器中一个很重要的量——卡尔曼增益K（Kalman Gain），用人话讲就是求差值y的权值。第一个公式中的R是测量噪声矩阵（measurement covariance matrix），这个表示的是测量值与真值之间的差值。一般情况下，传感器的厂家会提供。如果厂家未提供，我们也可以通过测试和调试得到。S只是为了简化公式，写的一个临时变量，不用太在意。

由于求得卡尔曼增益K需要使用到测量矩阵H，因此接下来的任务就是得到H。

毫米波雷达观测z是包含位置、角度和径向速度的3x1的列向量，状态向量x'是包含位置和速度信息的4x1的列向量，根据公式y=z-Hx'可知测量矩阵（Measurement Matrix）H的维度是3行4列。即：

 

从上面的公式很容易看出，等式两边的转化是非线性的，并不存在一个常数矩阵H，能够使得等式两边成立。

如果将高斯分布作为输入，输入到一个非线性函数中，得到的结果将不再符合高斯分布，也就将导致卡尔曼滤波器的公式不再适用。因此我们需要将上面的非线性函数转化为近似的线性函数求解。

图片出处：优达学城（Udacity）无人驾驶工程师学位

 

在大学课程《高等数学》中我们学过，非线性函数y=h(x)可通过泰勒公式在点(x0,y0)处展开为泰勒级数：

忽略二次以上的高阶项，即可得到近似的线性化方程，用以替代非线性函数h(x)，即：

将非线性函数h(x)拓展到多维，即求各个变量的偏导数，即：

对x求偏导数所对应的这一项被称为雅可比（Jacobian）式。

我将求偏导数的公式与我们的之前推导的公式对应起来看x的系数，会发现这里的测量矩阵H其实就是泰勒公式中的雅可比式。

多维的雅可比式的推导过程有兴趣的同学可以自己研究一下，这里我们直接使用其结论：

求得非线性函数h(x')对px，py，vx，vy的一阶偏导数，并排列成的矩阵，最终得到雅克比（Jacobian）矩阵H：

其中

接下来就是考验各位高等数学求偏导数功底的时候了！

经过一系列计算，最终得到测量矩阵H为：

根据以上公式可知，在每次预测障碍物的状态后，需要根据预测的位置和速度计算出对应的测量矩阵H，这个测量矩阵为非线性函数h(x')在x'所在位置进行求导的结果。

再看卡尔曼滤波器的最后两个公式

这两个公式，实际上完成了卡尔曼滤波器的闭环，第一个公式是完成了当前状态向量x的更新，不仅考虑了上一时刻的预测值，也考虑了测量值，和整个系统的噪声，第二个公式根据卡尔曼增益K，更新了系统的不确定度P，用于下一个周期的运算，该公式中的I为与状态向量同维度的单位矩阵。

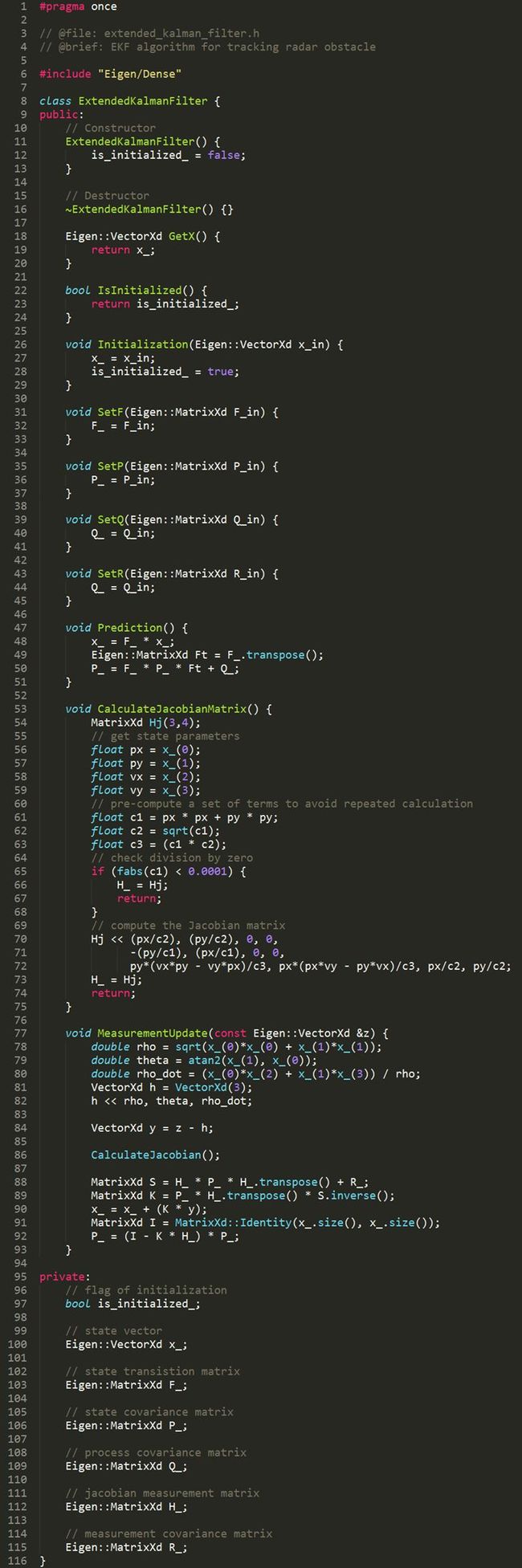
完成以上推导后，我们将推导的过程写成代码，如下所示：

再补上一些必要的代码，一个扩展卡尔曼滤波器的雏形就出来了，代码如下所示：

 

代码：使用扩展卡尔曼滤波器

以毫米波雷达数据为例，使用以上滤波器，代码如下：

其中GetRadarData函数除了获取毫米波雷达障碍物的距离、角度和径向速度外，还获取了信息采集时刻的时间戳，用于计算前后两帧的时间差delta_t。

以上就是使用扩展卡尔曼滤波器跟踪毫米波雷达障碍物的例子。

扩展卡尔曼（EKF）与经典卡尔曼（KF）的区别在于测量矩阵H的计算。EKF对非线性函数进行泰勒展开后，进行一阶线性化的截断，忽略了其余高阶项，进而完成非线性函数的近似线性化。正是由于忽略了部分高阶项，使得EKF的状态估计会损失一些精度。

只要你能够运用卡尔曼滤波器的7个经典公式，写出模型的F、P、Q、H、R矩阵，任何状态跟踪的问题都将迎刃而解。

---

结语

以上就是整个扩展卡尔曼滤波器的公式推导和代码编写过程。你会发现真正进行工程开发时，除了具备基本的写代码能力外，《高等数学》和《线性代数》中的理论知识也是必不可少的。下一期我会将经典卡尔曼滤波和扩展卡尔曼滤波结合起来实现激光雷达数据和毫米波雷达数据的融合。