梯度下降法基本原理

求解线性回归模型–函数求极值

• 解析解
  • 根据严格的推导和计算得到，是方程的精确解
  • 能够在任意精度下满足方程

但是在很多情况下，无法直接通过严格的公式推导，得到方程或者方程组的解析解，这时候只能够采用数值分析的方法得到近似解，这样的解也成为数值解

• 数值解
  • 通过某种近似计算得到的解
  • 能够在给定的精度条件下满足方程

我们就都介绍一种常用的求数值解的方法，梯度下降法。为了便于理解，我们先从最简单的一元凸函数开始介绍梯度下降法的求解过程。

一元凸函数求极值

这是一元函数fx=x平方+2的函数曲线，这种形状的函数称为凸函数，他一定存在唯一的一个极小值点，这个点在一个斜率正好为0的位置。在求解一个问题的时候，如果我们能够把它转换为在凸函数上求极小值的问题，那么这个问题就算已经破解了。在上节课中我们介绍了求这个函数的解析解的方法，下面我们来看一下，如何采用数值计算的方法来得到它的数值解。这类问题可以采用迭代的方法来求解。

这类问题可以采用迭代的方法来求解，首先我们在函数曲线上取任意1点$x_0$作为初值，当然这个初值不会恰好在极值点上。下面，我们按照某个步长移动x找到$x_1$，使得函数在$x_1$上的值，小于在$x_0$上的值。不断重复这个步骤，直到无法找到更小的函数值，最后找到的这个x，就是使函数达到极小值时的位置。

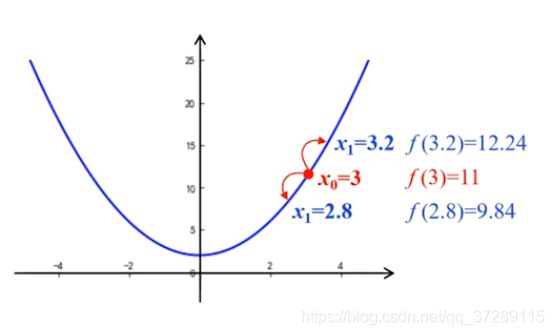
例如取初始值$x_0=3$，那么这一点的函数值等于11。假设取步长是0.2，那么x可能分别向两个方向移动，到达3.2或者2.8的位置，究竟应该向哪个方向移动呢？对比它们的函数值分别是显然9.84小于12.24。因此，取$x_1=2.8$。

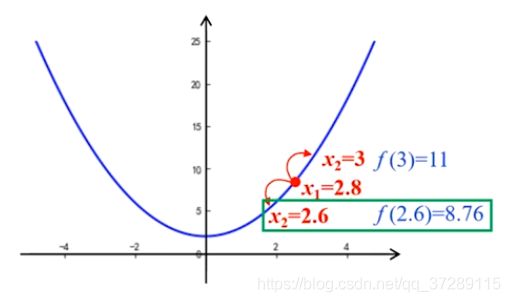
下面再以2.8为起点，步长仍然是0.2，对比函数，在$x=2.6$和$x=3$处的取值，显然，在$x=2.6$时的函数值更小。因此，取$x_2=2.6$。下面再以2.6为起点，继续这个步骤不断移动x，直到函数达到最小值，这个图只是个示意图，这个步长的比例是夸张了，其实每一步0.2是要比这个小很多。

为了更加严谨，我们用表格的形式来展示这个迭代的过程。

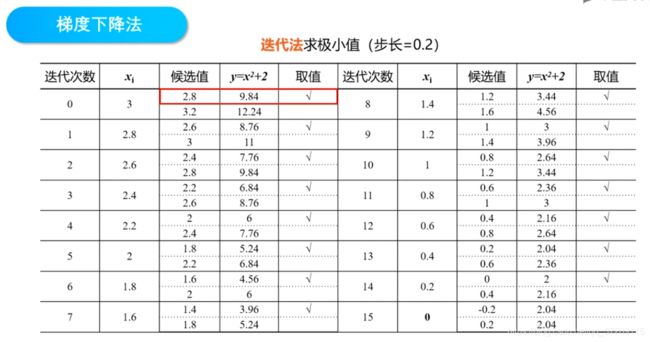
这是初值，x0=3，比较$x=2.8$和$x=3.2$对应的函数值，因为9.84小于12.24，所以选择$x_1=2.8$，进入下一次迭代，这时初值是2.8，根据函数值要不断减小的原则，选择$x_1=2.6$，再进入下一次迭代。不断重复这个步骤，在第15次迭代时，到达$x=0$。$x=0$时，函数值等于2。现在，无论往哪个方向移动，函数值都是2.04，比$x=0$时更大。也就是说，到这里之后，函数值不能再继续减小了。因此，当$x=0$时，$f(x)$就达到了最小值，迭代结束。

采用这种方法，需要通过多次迭代，不断的接近极值点，因此要花费比较长的时间，如果想要速度更快一点，可以把步长的值加大，例如把步长改为0.5。

那么，只要经过6次迭代就可以达到极小值点。可见步长取值越大，找到极值点的速度就越快，那么是不是不长的取值越大越好呢？我们将步长设为0.7来试一下

可以看到在第4次迭代时$x=0.2$，这时候可以取到的两个点分别是-0.5和0.9。取-0.5时函数值更小，因此下一步取-0.5，这时候比较$x=-1.2$和$x=0.2$时函数的取值，取0.2时函数值更小，因此又回到了0.2。继续进行这个过程会一直在0.2和-0.5之间来回震荡，无法达到极小值点。

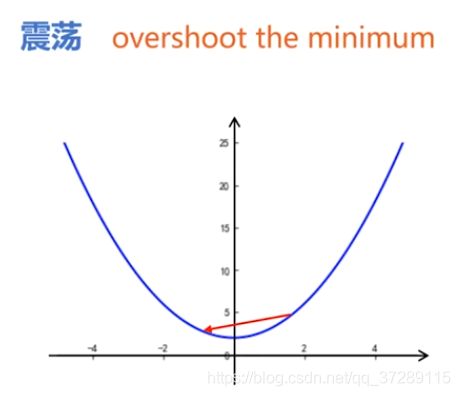
产生震荡的原因是因为更新x的时候，步长太大，一下子跨过了最小值。在英文资料中把这种情况称为overshoot the minimum。

震荡现象也分为两种情况，一种是虽然来回震荡，但是震幅越来越小，最后还是可以收敛。另一种就是来回震荡无法收敛。

通过这个例子我们发现，

• 步长如果太小会增加迭代次数，收敛速度很慢。
• 不长如果太大又会引起震荡，甚至导致无法收敛

那么这个不长的职能不能自动地调节呢，在距离及时点比较远的地方，步长的取值可以大一些，使得算法尽快收敛。在距离极值点比较近的地方，可以使步长逐渐减小，避免跨过极小值点发生震荡。这个想法显然不错，但是怎样才能够实现这种不长的自动调节呢？

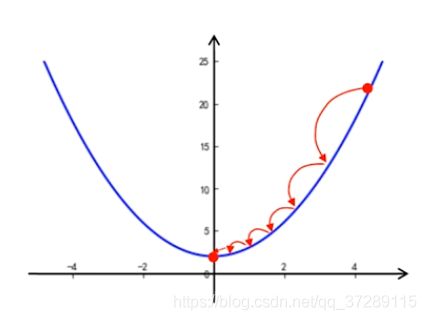
观察这个曲线可以发现，距离极值点比较远的地方，曲线比较陡峭，随着不断靠近极值点曲线逐渐变得平缓。曲线的陡峭程度可以用斜率表示，曲线越陡斜率越大，这时候我们希望步长也越大。曲线越平缓，斜率越小，我们希望步长也越小，因此只要用斜率去调节步长就可以了。

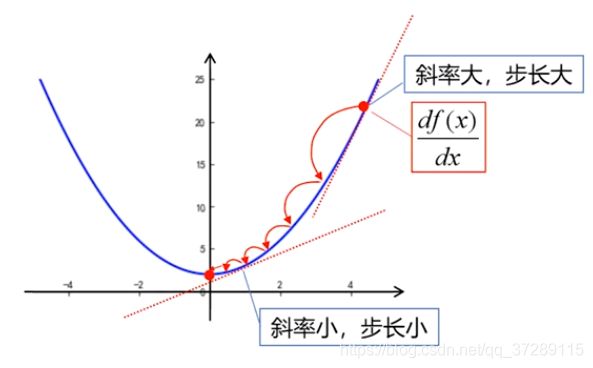
曲线在这一点的斜率就是函数在这个点的导数，让步长和斜率之间保持正比例关系。

$步长=\eta \frac{df(x)}{dx}$，$\eta$是一个常数，称为学习率。

就可以得到更新x的迭代公式$x^{(k+1)}=x^{(k)}-\eta \frac{df(x)}{dx}$

这里我们采用加括号的上标来表示迭代的次数，这是为了和之前采用下标表示样本序号，采用上标表示属性区分开来。在第k+1次迭代中，x的取值是由第k次x的值减去步长得到。

采用这种方法进行迭代，可以根据函数曲线的斜率实现，对步长的自适应调整，在这种迭代算法中，当x大于0时导数为正数。这时候，$x^{(k+1)}=x^{(k)}-a$，a为正数，变得更小，向原点的方向移动。

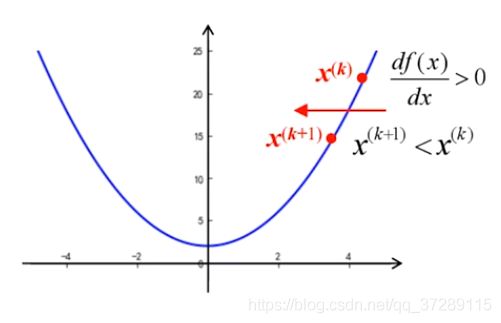
当x小于0时，导数为负数，$x^{(k+1)}=x^{(k)}-a$，a为负数，变得更大，x也是向原点的方向移动，

可见无论x是大于0还是小于0，最后都能够收敛于原点。采用这种方法导数的符号就直接决定了迭代更新的方向，而不需要像前面的例子那样，每次都去比较两个方向的函数值来确定x移动的方向。

总结一下，采用这种迭代算法能够自动调节步长，自动确定下一次更新的方向，并且能够保证收敛性。

这种一元凸函数求极值的方法可以推广到二元凸函数中，二元函数中有两个自变量$z=f(x,y)$，x和y需要分别进行迭代计算。
这是二元函数的迭代算法，
$x^{(k+1)}=x^{(k)}-\eta \frac{\partial f(x,y)}{\partial x}$

$y^{(k+1)}=y^{(k)}-\eta \frac{\partial f(x,y)}{\partial y}$

x的更新通过函数对x的偏导数来调节，y的更新通过函数对y的偏导数来调节。

函数f对x的偏导数和对y的偏导数，所组成的向量是二元函数的梯度。

• 导数：函数在某一点p的导数，其实就是函数在p点的变化率。

• 偏导数：$\frac{\partial f(x,y)}{\partial x}$二元函数对x的偏导数，就是函数在x方向上的变化率。
  $\frac{\partial f(x,y)}{\partial y}$对y的偏导数就是函数在y方向的变化率

• 方向导数：函数沿着某一个方向l的变化率，这个l可以是任何一个方向

x偏导数和y偏导数都是方向导数的特例，那么函数在p点时沿着哪一个方向的变化最快呢？也就是说哪一个方向导数最大，这个最大的值又是多少呢？这个问题的答案就是梯度。

• 梯度：$gradf(x,y)=\frac{\partial f}{\partial x}i+\frac{\partial f}{\partial y}j$
  梯度是一个矢量，既有大小又有方向，也可以采用这样的向量形式来表示.
  $\nabla =(\begin{array}{c}\frac{\partial f(x,y)}{\partial x}\\ \frac{\partial f(x,y)}{\partial y}\end{array})$
  • 它的大小就是所有方向导数中那个最大的值。
  • 它的方向就是取得最大方向导数的方向，或者说函数在某个点的梯度，就是指在这个点沿着这个方向的变化率最大。

这种二元函数求极值的迭代算法，其实就是每一步都是沿着梯度的方向移动，也就是沿着最陡的方向进行移动这样做计算的速度是最快的，这种方法被称为梯度下降法。

这就好像下山，我们在山腰上的某个位置环顾一圈之后，沿着当前最陡的方向，向下走一步。然后再环顾一圈，再沿着目前最陡的方向向下走一步。不断重复这个过程，保证每一步都是沿着当时最陡的方向向下走，那么一定可以以最少的步数到达山脚下，当然这要假设这个山的每个方向上都有路，都可以向下走。

对于机器学习算法，只要能够把损失函数描述成凸函数，那么就一定可以采用梯度下降法，以最快的速度更新模型参数，找到使损失函数达到最小值的点的位置。