神经网络求解优化问题,人工神经网络优化算法

想问一下，蚁群算法如何优化神经网络，最好能给一个matlap程序

蚁群算法(antcolonyoptimization,ACO)，又称蚂蚁算法，是一种用来在图中寻找优化路径的机率型算法。

它由MarcoDorigo于1992年在他的博士论文中提出，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。蚁群算法是一种模拟进化算法，初步的研究表明该算法具有许多优良的性质。

针对PID控制器参数优化设计问题，将蚁群算法设计的结果与遗传算法设计的结果进行了比较，数值仿真结果表明，蚁群算法具有一种新的模拟进化优化方法的有效性和应用价值。

程序已经上传到附件，手机看不到附件请用电脑下载。可以告诉你，这个程序内部有错，但是参考价值依然很大，因为大部分代码可以重用。我搞过蚁群算法，其实这个算法非常吃参数，如果参数不协调，效果很差。

建议你换种算法。

谷歌人工智能写作项目：小发猫

神经网络控制的书籍目录

rbsci。

第1章神经网络和自动控制的基础知识1.1人工神经网络的发展史1.1.120世纪40年代——神经元模型的诞生1.1.220世纪50年代——从单神经元到单层网络，形成第一次热潮1.1.320世纪60年代——学习多样化和AN2的急剧冷落1.1.420世纪70年代——在低迷中顽强地发展1.1.520世纪80年代——AN2研究热潮再度兴起1.1.620世纪90年代——再现热潮，产生许多边缘交叉学科1.1.7进入21世纪——实现机器智能的道路漫长而又艰难1.2生物神经元和人工神经元1.2.1生物神经元1.2.2人工神经元1.3生物神经网络和人工神经网络1.3.1生物神经网络1.3.2人工神经网络1.4自动控制的发展史1.4.1从传统控制理论到智能控制1.4.2智能控制的产生与基本特征1.4.3智能控制系统1.5模糊集与模糊控制概述1.5.1模糊集1.5.2模糊隶属函数1.5.3模糊控制1.6从生物神经控制到人工神经控制1.6.1生物神经控制的智能特征1.6.2人工神经控制的模拟范围1.7小结习题与思考题第2章神经计算基础2.1线性空间与范数2.1.1矢量空间2.1.2范数2.1.3赋范线性空间2.1.4L1范数和L2范数2.2迭代算法2.2.1迭代算法的终止准则2.2.2梯度下降法2.2.3最优步长选择2.3逼近论2.3.1Banach空间和逼近的定义2.3.2L2逼近和最优一致逼近2.3.3离散点集上的最小二乘逼近2.4神经网络在线迭代学习算法2.5Z变换2.5.1Z变换的定义和求取2.5.2Z变换的性质2.5.3Z反变换2.6李雅普诺夫意义下的稳定性2.6.1非线性时变系统的稳定性问题2.6.2李雅普诺夫意义下的渐进稳定2.6.3李雅普诺夫第二法2.6.4非线性系统的稳定性分析2.7小结习题与思考题第3章神经网络模型3.1人工神经网络建模3.1.1MP模型3.1.2Hebb学习法则3.2感知器3.2.1单层感知器3.2.2多层感知器3.3BP网络与BP算法3.3.1BP网络的基本结构3.3.2BP算法及步长调整3.4自适应线性神经网络3.5自组织竞争型神经网络3.5.1自组织竞争型神经网络的基本结构3.5.2自组织竞争型神经网络的学习算法3.6小脑模型神经网络3.6.1CMAC的基本结构3.6.2CMAC的工作原理3.6.3CMAC的学习算法与训练3.7递归型神经网络3.7.1DTRNN的网络结构3.7.2实时递归学习算法3.8霍普菲尔德（Hopfield）神经网络3.8.1离散型Hopfield神经网络3.8.2连续型Hopfield神经网络3.8.3求解TSP问题3.9小结习题与思考题第4章神经控制中的系统辨识4.1系统辨识基本原理4.1.1辨识系统的基本结构4.1.2辨识模型4.1.3辨识系统的输入和输出4.2系统辨识过程中神经网络的作用4.2.1神经网络辨识原理4.2.2多层前向网络的辨识能力4.2.3辨识系统中的非线性模型4.3非线性动态系统辨识4.3.1非线性动态系统的神经网络辨识4.3.2单输入单输出非线性动态系统的BP网络辨识4.4多层前向网络辨识中的快速算法4.5非线性模型的预报误差神经网络辨识4.5.1非动态模型建模，4.5.2递推预报误差算法4.6非线性系统逆模型的神经网络辨识4.6.1系统分析逆过程的存在性4.6.2非线性系统的逆模型4.6.3基于多层感知器的逆模型辨识4.7线性连续动态系统辨识的参数估计4.7.1Hopfield网络用于辨识4.7.2Hopfield网络辨识原理4.8利用神经网络联想功能的辨识系统4.8.1二阶系统的性能指标4.8.2系统辨识器基本结构4.8.3训练与辨识操作4.9小结习题与思考题第5章人工神经元控制系统5.1人工神经元的PID调节功能5.1.1人工神经元PID动态结构5.1.2人工神经元闭环系统动态结构5.2人工神经元PID调节器5.2.1比例调节元5.2.2积分调节元5.2.3微分调节元5.3人工神经元闭环调节系统5.3.1系统描述5.3.2Lyapunov稳定性分析5.4人工神经元自适应控制系统5.4.1人工神经元自适应控制系统的基本结构5.4.2人工神经元自适应控制系统的学习算法5.5人工神经元控制系统的稳定性5.6小结习题与思考题第6章神经控制系统6.1神经控制系统概述6.1.1神经控制系统的基本结构6.1.2神经网络在神经控制系统中的作用6.2神经控制器的设计方法6.2.1模型参考自适应方法6.2.2自校正方法6.2.3内模方法6.2.4常规控制方法6.2.5神经网络智能方法6.2.6神经网络优化设计方法6.3神经辨识器的设计方法6.4PID神经控制系统6.4.1PID神经控制系统框图6.4.2PID神经调节器的参数整定6.5模型参考自适应神经控制系统6.5.1两种不同的自适应控制方式6.5.2间接设计模型参考自适应神经控制系统6.5.3直接设计模型参考自适应神经控制系统6.6预测神经控制系统6.6.1预测控制的基本特征6.6.2神经网络预测算法6.6.3单神经元预测器6.6.4多层前向网络预测器6.6.5辐射基函数网络预测器6.6.6Hopfield网络预测器6.7自校正神经控制系统6.7.1自校正神经控制系统的基本结构6.7.2神经自校正控制算法6.7.3神经网络逼近6.8内模神经控制系统6.8.1线性内模控制方式6.8.2内模控制系统6.8.3内模神经控制器6.8.4神经网络内部模型6.9小脑模型神经控制系统6.9.1CMAC控制系统的基本结构6.9.2CMAC控制器设计6.9.3CMAC控制系统实例6.10小结习题与思考题第7章模糊神经控制系统7.1模糊控制与神经网络的结合7.1.1模糊控制的时间复杂性7.1.2神经控制的空间复杂性7.1.3模糊神经系统的产生7.2模糊控制和神经网络的异同点7.2.1模糊控制和神经网络的共同点7.2.2模糊控制和神经网络的不同点7.3模糊神经系统的典型结构7.4模糊神经系统的结构分类7.4.1松散结合7.4.2互补结合7.4.3主从结合7.4.4串行结合7.4.5网络学习结合7.4.6模糊等价结合7.5模糊等价结合中的模糊神经控制器7.5.1偏差P和偏差变化率Δe的获取7.5.2隶属函数的神经网络表达7.6几种常见的模糊神经网络7.6.1模糊联想记忆网络7.6.2模糊认知映射网络7.7小结习题与思考题第8章神经控制中的遗传进化训练8.1生物的遗传与进化8.1.1生物进化论的基本观点8.1.2进化计算8.2遗传算法概述8.2.1遗传算法中遇到的基本术语8.2.2遗传算法的运算特征8.2.3遗传算法中的概率计算公式8.3遗传算法中的模式定理8.3.1模式定义和模式的阶8.3.2模式定理（Schema）8.4遗传算法中的编码操作8.4.1遗传算法设计流程8.4.2遗传算法中的编码规则8.4.3一维染色体的编码方法8.4.4二维染色体编码8.5遗传算法中的适应度函数8.5.1将目标函数转换成适应度函数8.5.2标定适应度函数8.6遗传算法与优化解8.6.1适应度函数的确定8.6.2线性分级策略8.6.3算法流程8.7遗传算法与预测控制8.8遗传算法与神经网络8.9神经网络的遗传进化训练8.9.1遗传进化训练的实现方法8.9.2BP网络的遗传进化训练8.10小结习题与思考题附录常用神经控制术语汉英对照参考文献……

求人工神经网络的具体算法，数学模型，比如求一个函数最优值之类的，不要各种乱七八糟的介绍，谢谢

神经网络就像多项式或者线性模型一样，是个看不见表达式的模型，它的表达式就是网络，它比一般模型具有更高的自由度和弹性；同时它是一个典型的黑箱模型方法；比多项式等模型还黑。

优化算法，就是寻优的算法，所谓寻优过程，就是寻找使目标函数最小时（都是统一表示成寻找使函数具有最小值）的自变量的值。

回归或者拟合一个模型,例如用一个多项式模型去拟合一组数据，其本质就是寻找使残差平方和最小的参数值，这就是一个寻优的过程，其实就是寻找使函数F（x）值最小时的x的值；对于这个具体的寻找过程就涉及到算法问题，就是如何计算。

所谓算法，是数值分析的一个范畴，就是解这问题的方法；例如一个一元二次方程x^2-3x+1=0的解法，因为简单可以直接求解，也可以用牛顿逐个靠近的方法求解，也即是迭代，慢慢接近真实解，如此下去不断接近真值，要注意迭代算法是涉及算法精度的，这些迭代算法是基于计算机的，算法的初衷也是用近似的算法用一定的精度来接近真实值。

比如上面的方程也可以用遗传算法来解，可以从一些初始值最终迭代到最佳解。

神经网络在寻找网络的参数即权值的时候，也有寻找使训练效果最好的过程，这也是寻优的过程，这里涉及到了算法就是所谓的神经网络算法，这和最小二乘算法是一样的道理；例如做响应面的时候，其实就是二次回归，用最小二乘得到二次模型的参数，得到一个函数，求最大产物量就是求函数模型的最大值，怎么算呢？

顶点处如果导数为0，这个地方对应的x值就是最优的，二次模型简单可以用偏导数=0来直接解决，这过程也可以遗传算法等来解决。说到底所谓寻优的本质就是，寻找函数极值处对应的自变量的值。

bp神经网络的算法改进一共有多少种啊！麻烦举例一下！

。

改进点主要在以下几个方面1激励函数的坡度———————误差曲面的平台和不收敛现象————————————————激励函数中引入陡度因子，分段函数做激励函数2误差曲面——————误差平方做目标函数，逼近速度慢，过拟合————————————————标准误差函数中加入惩罚项————————————————信息距离和泛化能力之间的关系，构建新的神经网络学习函数3网络初始权值的选取—————————通常在【0,1】间选取，易陷入局部最小—————————————————复合算法优化初始权值—————————————————Cauchy不等式和线性代数方法得最优初始权值4改进优化算法————————标准BP采用梯度下降法，局部最小收敛慢——————————————————共扼梯度法、Newton法、Gauss一Ncwton法、Lvenber_Marquardt法、快速传播算法——————————————————前馈网络学习算法，二阶学习算法，三项BP算法，最优学习参数的BP算法。

5.优化网络结构————————拓扑结构中网络层数、各层节点数、节点连接方式的不确定性——————————————构造法和剪枝法（权衰减法、灵敏度计算方法等）——————————————网络结构随样本空间进行变换，简化网络结构6混合智能算法————————与遗传算法、进化计算、人工免疫算法、蚁群算法、微粒群算法、————————模糊数学、小波理论、混沌理论。

细胞神经网络。

bp神经网络用啥算法？

自己找个例子算一下，推导一下，这个回答起来比较复杂神经网络对模型的表达能力依赖于优化算法，优化是一个不断计算梯度并调整可学习参数的过程，Fluid中的优化算法可参考 优化器 。

在网络的训练过程中，梯度计算分为两个步骤：前向计算与 反向传播 。前向计算会根据您搭建的网络结构，将输入单元的状态传递到输出单元。

反向传播借助 链式法则 ，计算两个或两个以上复合函数的导数，将输出单元的梯度反向传播回输入单元，根据计算出的梯度，调整网络的可学习参数。BP算法隐层的引入使网络具有很大的潜力。

但正像Minskey和Papert当时所指出的．虽然对所有那些能用简单(无隐层)网结解决的问题有非常简单的学习规则，即简单感知器的收敛程序(主要归功于Widrow和HMf于1960年提出的Delta规刚)，BP算法但当时并没有找到同样有技的含隐层的同培的学习规则。

对此问题的研究有三个基本的结果。一种是使用简单无监督学习规则的竞争学习方法．但它缺乏外部信息．难以确定适台映射的隐层结构。第二条途径是假设一十内部(隐层)的表示方法，这在一些先约条件下是台理的。

另一种方法是利用统计手段设计一个学习过程使之能有技地实现适当的内部表示法，Hinton等人(1984年)提出的Bolzmann机是这种方法的典型例子．它要求网络在两个不同的状态下达到平衡，并且只局限于对称网络。

Barto和他的同事(1985年)提出了另一条利用统计手段的学习方法。

但迄今为止最有教和最实用的方瑶是Rumelhart、Hinton和Williams(1986年)提出的一般Delta法则，即反向传播(BP)算法。

Parter(1985年)也独立地得出过相似的算法,他称之为学习逻辑。此外，Lecun(1985年)也研究出大致相似的学习法则。

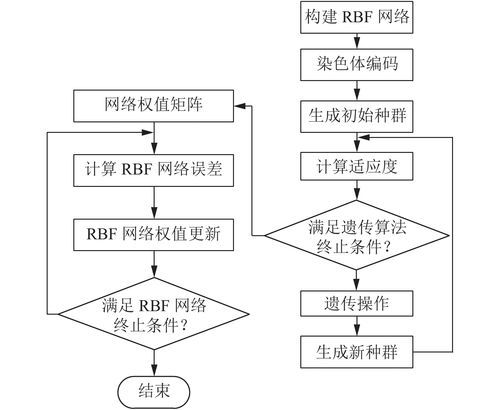
matlab的遗传算法优化BP神经网络

对y=x1^2+x2^2非线性系统进行建模，用1500组数据对网络进行构建网络，500组数据测试网络。由于BP神经网络初始神经元之间的权值和阈值一般随机选择，因此容易陷入局部最小值。

本方法使用遗传算法优化初始神经元之间的权值和阈值，并对比使用遗传算法前后的效果。

步骤：未经遗传算法优化的BP神经网络建模1、随机生成2000组两维随机数(x1,x2)，并计算对应的输出y=x1^2+x2^2，前1500组数据作为训练数据input_train，后500组数据作为测试数据input_test。

并将数据存储在data中待遗传算法中使用相同的数据。2、数据预处理：归一化处理。3、构建BP神经网络的隐层数，次数，步长，目标。

4、使用训练数据input_train训练BP神经网络net。