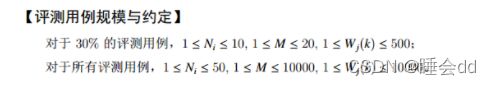2020年第十一届蓝桥杯大赛python组省赛真题（更新中）

目录

1. 试题A：门牌制作

2. 试题B：寻找2020

3. 试题C：跑步锻炼

4. 试题D：蛇形填数

5. 试题E：排序

6. 试题F：成绩统计

7. 试题G：单词分析

8. 试题H：数字三角形

9. 试题I：平面切分

11.回文日期

12. 成绩分析

13. 既约分数

14. 七段码

15. 子串分值 

16. 作物杂交

17. 字符计数

18. 约数个数

19.长草

---

1. 试题A：门牌制作

这个很好做，直接暴力求解

代码：

result=0
for i in range(1,2021):
      result=result+str(i).count('2')

print(result)

答案：624

2. 试题B：寻找2020

 代码：暴力求解

l = []
with open('2020.txt') as fp:
    for line in fp.readlines():
        l.append(list(line.strip()))

s = len(l)  #301
q = len(l[1])#300
count = 0

for i in range(s-1):  #行
    for j in range(q-3): 
        if (l[i][j] == '2' and l[i][j+1] == '0' and l[i][j+2]=='2' and l[i][j+3]=='0'):
            count = count+1
for i in range(q-3):  #列
    for j in range(s-1): 
        if (l[i][j] == '2' and l[i+1][j] == '0' and l[i+2][j]=='2' and l[i+3][j]=='0'):
            count = count+1
for i in range(q-3):  #左上到右下
    for j in range(q-3): 
        if (l[i][j] == '2' and l[i+1][j+1] == '0' and l[i+2][j+2]=='2' and l[i+3][j+3]=='0'):
            count = count+1
print(count)

答案：16520

3. 试题C：跑步锻炼

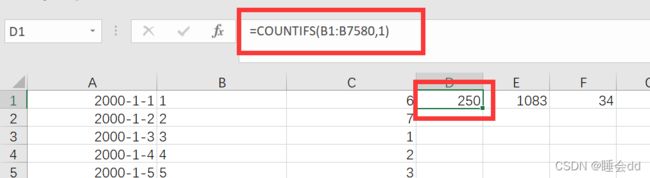
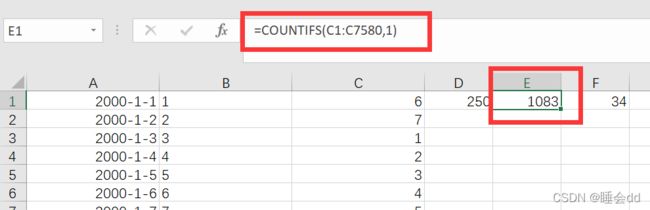
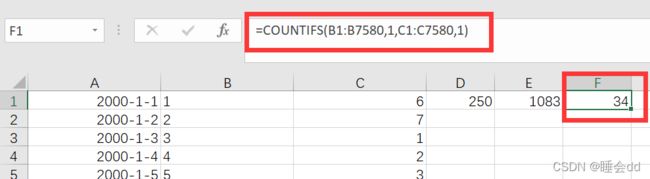
 这个题我觉得用excel来算比写代码要简单

最终答案：8879

先在第一列中把日期列出来，2000-1-1，2000-1-2，然后往下拖一直拖到2020-10-1。然后用text函数把日期中的日给提取出来。用weekday函数把星期提取出来。然后用countifs算出来有几个月初，有几个周一，有几个既是月初又是周一。最后答案就是用总天数加上月初的个数，加上周一的个数，减去既是月初又是周一的个数。

第一列是日期，第二列是日，第三列是礼拜，第四列是有几个月初，第五列是有几个礼拜一，第六列是有几个既是月初又是礼拜一的日子。

 第二列公式：

第三列公式：

 第四列公式：

第五列公式：

 第六列公式：

 最后答案是7580+250+1083-34=8879

4. 试题D：蛇形填数

 这个直接手算就可以很简单

答案：761

5. 试题E：排序

全逆乱序的冒泡排序次数为N*(N-1)/2

15*14/2=105

14*13/2=91

100次交换至少需要15个字母 onmlkjihgfedcba

105-100=5,

只需把第6个字母往后移到第1位即可

6. 试题F：成绩统计

 

 这个题很简单，一点思维量都没有

代码：

n=int(input())

youxiu=0
jige=0
for i in range(n):
      m=int(input())
      if m>=60:
            jige=jige+1
            if m>=85:
                  youxiu=youxiu+1
      

jigelv=round(jige*100/n)
youxiulv=round(youxiu*100/n)
print(str(jigelv)+'%')
print(str(youxiulv)+'%')

7. 试题G：单词分析

 本题也相对来说比较简单，我先创建一个set集合l，把输入的单词中每一个字母都加入l里面。这样就得到了输入单词的所有不重复字母。然后把集合l转换为列表ll，对列表ll排序，这样在我接下来判断出现次数最多的字母有多个时，可以保证我输出的是字典序最小的那一个。

代码：

s=input()
l=set()
for i in s:
      l.add(i)

ll=list(l)
ll.sort()
maxsum=0
k=''
for j in ll:
      if s.count(j)>maxsum:
            maxsum=s.count(j)
            k=j

print(k)
print(maxsum)

8. 试题H：数字三角形

代码：

n=int(input())
l=[]
for i in range(n):
      l.append(list(map(int,input().split())))

dp=[[1]*j for j in range(1,n+1)]
dp[0][0]=l[0][0]
for i in range(1,n):
      for j in range(i+1):
            if j==0:
                  dp[i][j]=dp[i-1][j]+l[i][j]
            elif j==i:
                  dp[i][j]=dp[i-1][j-1]+l[i][j]
            else:
                  dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+l[i][j]

if n%2==0:
      print(max(dp[n-1][n//2-1],dp[n-1][n//2]))
else:
      print(dp[n-1][n//2])

9. 试题I：平面切分

 

代码：

import sys
n = int(input())
lines = []
for i in range(n):
    a, b = list(map(int, input().split()))
    lines.append((a, b))
lines = list(set(lines))#这里是去掉重复直线
n = len(lines)
def getnode(lines1, lines2):#得到两条直线交点，若平行，返回None
    A1 = lines1[0]
    B1 = lines1[1]
    A2 = lines2[0]
    B2 = lines2[1]
    if A1 - A2 == 0:
        return 
    x = (B2 - B1) / (A1 - A2)
    y = A1 * x + B1
    x = round(x, 10)
    y = round(y, 10)
    return (x, y)
ci = [1] * (n + 1)
node = set()
for i in range(1, n):
    node.clear()
    for j in range(i):
        tmp = getnode(lines[i], lines[j])
        if tmp == None: continue
        node.add(tmp)
    ci[i] += len(node)
        
print(sum(ci[:n]) + 1)        

10. 

 

 

11.回文日期

题目描述

2020 年春节期间，有一个特殊的日期引起了大家的注意：2020 年 2 月 2 日。因为如果将这个日期按 “yyyymmdd” 的格式写成一个 8 位数是 20200202，恰好是一个回文数。我们称这样的日期是回文日期。

有人表示 20200202 是 “千年一遇” 的特殊日子。对此小明很不认同，因为不到 2 年之后就是下一个回文日期：20211202 即 2021 年 12 月 2 日。

也有人表示 20200202 并不仅仅是一个回文日期，还是一个 ABABBABA 型的回文日期。对此小明也不认同，因为大约 100 年后就能遇到下一个 ABABBABA 型的回文日期：21211212 即 2121 年 12 月 12 日。算不上 “千年一遇”，顶多算 “千年两遇”。

给定一个 8 位数的日期，请你计算该日期之后下一个回文日期和下一个 ABABBABA 型的回文日期各是哪一天。

输入描述

输入包含一个八位整数 N，表示日期。

对于所有评测用例，10000101≤N≤89991231，保证 N 是一个合法日期的 8 位数表示。

输出描述

输出两行，每行 1 个八位数。第一行表示下一个回文日期，第二行表示下一个 ABABBABA 型的回文日期。

输入输出样例

示例

输入

20200202

输出

20211202
21211212

运行限制

• 最大运行时间：1s
• 最大运行内存: 256M

12. 成绩分析

题目描述

小蓝给学生们组织了一场考试，卷面总分为 100 分，每个学生的得分都是一个 0 到 100 的整数。

请计算这次考试的最高分、最低分和平均分。

输入描述

输入的第一行包含一个整数 n (1≤n≤104)，表示考试人数。

接下来 n 行，每行包含一个 0 至 100 的整数，表示一个学生的得分。

输出描述

输出三行。

第一行包含一个整数，表示最高分。

第二行包含一个整数，表示最低分。

第三行包含一个实数，四舍五入保留正好两位小数，表示平均分。

输入输出样例

示例

输入

7
80
92
56
74
88
99
10

输出

99
10
71.29

运行限制

• 最大运行时间：1s
• 最大运行内存: 256M

代码：（比较简单）

n=int(input())
s=[]
for i in range(n):
    s.append(int(input()))
print(max(s))
print(min(s))
print("{:.2f}".format(sum(s)/n))

13. 既约分数

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

如果一个分数的分子和分母的最大公约数是 1，这个分数称为既约分数。

例如 4/3​,8/1​,1/7​， 都是既约分数。

请问，有多少个既约分数，分子和分母都是 1 到 2020 之间的整数（包括 1 和 2020）？

运行限制

• 最大运行时间：2s
• 最大运行内存: 128M

代码：比较简单

import math
ans=4039
for i in range(2,2021):
    for j in range(2,2021):
        if math.gcd(i,j)==1:
            ans=ans+1
print(ans)
            
    

答案：2481215

14. 七段码

 代码：参考的蓝桥官网别人发布的题解

dic = {'a':['b','f'],
'b':['a','g','c'],
'c':['g','d','b'],
'd':['c','e'],
'e':['f','g','d'],
'f':['a','g','e'],
'g':['f','b','e','c']}
ans = set()
def dfs(arr,now):
    ans.add(str(sorted(arr)))
    for i in dic[now]:
        if i not in arr:
            arr.append(i)
            dfs(arr,i)
            arr.remove(i)
for i in 'abcdefg':dfs([i],i)
print(len(ans))

15. 子串分值 

我自己就是按照简单的思想，找到每一个子串，对子串每一个字母出现的次数进行检查，等于1就加一次。但是这样会超时。

我自己写的超时代码：

s=input()
result=len(s)

for i in range(2,len(s)+1):#i是子串长度
    for j in range(0,len(s)-i+1):
        s1=s[j:j+i]
        result=result+len(set(s1))
print(result)

我在蓝桥练习官网上找到的别人写的正确代码：

# 输入元素
s=input()
a=[-1 for i in range(26)]
count=0
for i in range(len(s)):
  index=ord(s[i])-ord('a')
  count+=(len(s)-i)*(i-a[index])
  a[index]=i
print(count)

s = input()
n = len(s)
dp = [0]*(n+1)
readed = [n]*26  # 作用：将已遍历的字符与未遍历的字符统一计算
for i in range(n-1, -1, -1):
  dp[i] = dp[i+1] + readed[ord(s[i]) - 97] - i  # 第i个字符开头时出现n-i次
  readed[ord(s[i]) - 97] = i  # 标记该字符最近一次出现的位置
print(sum(dp))

上面这俩我都没太看明白啊。。。

16. 作物杂交

题目描述

作物杂交是作物栽培中重要的一步。已知有 N 种作物 (编号 1 至 N )，第 i 种作物从播种到成熟的时间为 Ti​。作物之间两两可以进行杂交，杂交时间取两种中时间较长的一方。如作物 A 种植时间为 5 天，作物 B 种植时间为 7 天，则 AB 杂交花费的时间为 7 天。作物杂交会产生固定的作物，新产生的作物仍然属于 N 种作物中的一种。

初始时，拥有其中 M 种作物的种子 (数量无限，可以支持多次杂交)。同时可以进行多个杂交过程。求问对于给定的目标种子，最少需要多少天能够得到。

如存在 4 种作物 ABCD，各自的成熟时间为 5 天、7 天、3 天、8 天。初始拥有 AB 两种作物的种子，目标种子为 D，已知杂交情况为 A × B → C，A × C → D。则最短的杂交过程为：

第 1 天到第 7 天 (作物 B 的时间)，A × B → C。

第 8 天到第 12 天 (作物 A 的时间)，A × C → D。

花费 12 天得到作物 D 的种子。

输入描述

输入的第 1 行包含 4 个整数 N,M,K,T，N 表示作物种类总数 (编号 1 至 N)，M 表示初始拥有的作物种子类型数量，K 表示可以杂交的方案数，T 表示目标种子的编号。

第 2 行包含 N 个整数，其中第 i 个整数表示第 i 种作物的种植时间 Ti​ (1≤Ti​≤100)。

第 3 行包含 M 个整数，分别表示已拥有的种子类型 Kj​ (1≤Kj​≤M)，Kj​ 两两不同。

第 4 至 K + 3 行，每行包含 3 个整数 A, B,C，表示第 A 类作物和第 B 类作物杂交可以获得第 C 类作物的种子。

其中，1≤N≤2000,2≤M≤N,1≤K≤105,1≤T≤N, 保证目标种子一定可以通过杂交得到。

输出描述

输出一个整数，表示得到目标种子的最短杂交时间。

输入输出样例

示例

输入

6 2 4 6
5 3 4 6 4 9
1 2
1 2 3
1 3 4
2 3 5
4 5 6

输出

16

样例说明

第 1 天至第 5 天，将编号 1 与编号 2 的作物杂交，得到编号 3 的作物种子。

第 6 天至第 10 天，将编号 1 与编号 3 的作物杂交，得到编号 4 的作物种子。

第 6 天至第 9 天，将编号 2 与编号 3 的作物杂交，得到编号 5 的作物种子。

第 11 天至第 16 天，将编号 4 与编号 5 的作物杂交，得到编号 6 的作物种子。

总共花费 16 天。

运行限制

• 最大运行时间：2s
• 最大运行内存: 256M

思想：就是从目标作物开始往下递归，一直递归到有初始种子的时候。

代码：

import collections
n,m,k,t=map(int,input().split())
zhongtime=list(map(int,input().split()))
zhongtime.insert(0,0)
have=set(map(int,input().split()))
rule=collections.defaultdict(list)

for i in range(k):
    f,m,s=map(int,input().split())
    rule[s].append(f)
    rule[s].append(m)
    
def dfs(seed):
    if seed in have:
        return 0
    min_time=float("inf")        
    tmp=max(zhongtime[rule[seed][0]],zhongtime[rule[seed][1]])
    min_t=max(dfs(rule[seed][0]),dfs(rule[seed][1]))+tmp
    if min_t

17. 字符计数

 代码：（简单）

s=input()
count=0
yuan="aeiou"
for i in s:
      if i in yuan:
            count+=1
print(count)
print(len(s)-count)

18. 约数个数

代码：

count=0
for i in range(1,1100):
      if 1200000%i==0:
            count=count+2
print(count)
            

 答案：96

19.长草

题目描述

小明有一块空地，他将这块空地划分为 n 行 m 列的小块，每行和每列的长度都为 1。

小明选了其中的一些小块空地，种上了草，其他小块仍然保持是空地。

这些草长得很快，每个月，草都会向外长出一些，如果一个小块种了草，则它将向自己的上、下、左、右四小块空地扩展，

这四小块空地都将变为有草的小块。请告诉小明，k 个月后空地上哪些地方有草。

输入描述

输入的第一行包含两个整数 n,m。

接下来n 行，每行包含 m 个字母，表示初始的空地状态，字母之间没有空格。如果为小数点，表示为空地，如果字母为 g，表示种了草。

接下来包含一个整数 k。 其中，2≤n,m≤1000，1≤k≤1000。

输出描述

输出 n 行，每行包含 m 个字母，表示 k 个月后空地的状态。如果为小数点，表示为空地，如果字母为 g，表示长了草。

输入输出样例

示例

输入

4 5
.g...
.....
..g..
.....
2

输出

gggg.
gggg.
ggggg
.ggg.

运行限制

• 最大运行时间：1s
• 最大运行内存: 256M

我自己按照挨个遍历的方式写的代码：（会超时）

n,m=map(int,input().split())
s=[]
for i in range(n):
     s.append(list(input()))         
k=int(input())
s1=[s[i][:] for i in range(n)] 

for i in range(0,k):
      for a in range(0,n):
            for b in range(0,m):
                  if s[a][b]=='g':
                        
                        s1[a][b]='g'
                        if a-1>=0:
                              s1[a-1][b]='g'
      
                        if a+1=0:
                              s1[a][b-1]='g'
                                                       
                        if b+1

通过写上面这个代码，我又学到了一些知识点。如下：

python的字符串赋值给一个变量s以后，可以通过s[0],s[1]这样的方式来访问字符串s中的单个字符。但是却不能通过给s[0],s[1]赋值这样的方式来改变字符串中的单个字符。

要想改变字符串中的单个字符，必须先把字符串转换为列表，通过列表去改变单个字符，然后再将列表转换为字符串，达到改变字符串中某个字符的目的。

生成列表的副本：不能用list1=list2这样的方式去做，这样会让list1和list2都指向同一个列表，改变一个的话，另一个也就改变了。应该用下面的方式：

一维列表：list2=list1[:]

二维列表：假设列表有n行，m列。list2=[i[:] for i in list1]

下面是我看了别人的方法后写出来的代码：

不要一个个去判断，是‘g'就扩散到四周，而是在开始输入字符串的时候就把那些'g'加到一个集合中，对集合里面的每一个位置进行四周扩散。

n, m = map(int, input().split())
s = [['.' for _ in range(m)] for _ in range(n)]
a = []
b = set()
for i in range(n):
    input_ = input()
    for j in range(m):
        #s[i][j] = input_[j]
        if input_[j] == 'g':
              s[i][j]='g'                          
              b.add((i, j))
k=int(input())
while k>0:
      a=list(b)
      b=set()
      for mm in a:
            x,y=mm
            if x>0 and s[x-1][y]!='g':
                  s[x-1][y]='g'
                  b.add((x-1,y))
            if x0 and  s[x][y-1]!='g':
                  s[x][y-1]='g'
                  b.add((x,y-1))
            if y

下面这个是用bfs做的：

import os
import sys
m, n = map(int, input().split())#输入行m,列n
data = []#输入数据
queue = []#队列
for i in range(m):
    data.append(list(input()))#逐行输入
k = int(input())#输入月
for i in range(m):
    for j in range(n):
        if data[i][j] == 'g':
            queue.append((i, j))#初始化队列中的草
dirs = [(0, 1), (0, -1), (1, 0), (-1, 0)]#四个方向


def bfs():
    t = len(queue)#队列长度
    while t > 0:
        temp = queue.pop(0)
        x1, y1 = temp[0], temp[1]
        for d in dirs:#四个方向
            nx = x1+d[0]#nextx下一个方向
            ny = y1+d[1]
            if nx >= 0 and nx < m and ny >= 0 and ny < n and data[nx][ny] == '.':#如果没越界，且该方向为'.'
                data[nx][ny] = 'g'#将该位置赋值
                queue.append((nx, ny))#新的位置入队
        t -= 1


for i in range(k):
    bfs()#循环k个月
for i in range(m):
    print(''.join(data[i]))

20. 斐波那契数列最大公约数

简单

代码：

import math
f=[0,1,1]
f1=f[1]
f2=f[2]
for i in range(1,2021):

    f3=f1+f2
    f.append(f3)
    f1=f2
    f2=f3

result=math.gcd(f[2020],f[520])
print(result)
    

答案：6765

21. 单词重排

 这个单词中有7个字母，有两个重复的字母a。

因此答案为7*6*5*4*3*2*1/2

不知道为啥的可以举个例子，比如说：

abc可以排列3*2*1=6种

aab可以排列3种

abcd可以排列4*3*2*1=24种

aabc可以排列12种。

可以发现有同样数量的字母，字母完全不同的排列种数是仅有两个重复字母排列种数的2倍。

22.反倍数

 代码：

n=int(input())
a,b,c=map(int,input().split())
count=0
for i in range(1,n+1):
    if i%a!=0 and i%b!=0 and i%c!=0:
        count+=1
print(count)

23. 洁净数

代码：

import os
import sys

# 请在此输入您的代码
n=int(input())
count=0
for i in range(1,n+1):
    
    if '2' not in str(i):
        count+=1
print(count)

 

24.凯撒加密

代码：

s=input()
s1=[]
for i in s:
    if ord(i)>ord('w'):
        s1.append(chr(ord(i)-23))
    else:
        s1.append(chr(ord(i)+3))
s=''.join(s1)
print(s)

 25. 最大距离

代码：

n=int(input())
s=list(map(int,input().split()))
vis=0
for i in range(n-1):
    for j in range(i+1,n):
        tmp=abs(i-j)+abs(s[i]-s[j])
        if tmp>vis:
            vis=tmp
print(vis)

26. 数位递增的数

代码：

n=int(input())
count=0
for i in range(1,n):
    a=list(str(i))
    if a==sorted(a):
        count+=1
print(count)

 27. 音节判断

 代码：

s = input()
count = 0
lst = ['a','e','i','o','u']
for i in range(0, len(s)-1):
    if s[0] not in lst and s[-1] in lst:
        if s[i] not in lst and s[i+1] in lst:           # 辅音字母 元音字母 挨着的情况只有两次
            count += 1

if count == 2:
    print('yes')
else:
    print('no')

28.