2017年第八届蓝桥杯省赛题目python解答（更新中）

目录

1. 迷宫

2. 跳蚱蜢

3. 魔方状态

 4. 方格分割

5. 正则表达式

6. 包子凑数

---

··

1. 迷宫

 

思路：使用暴力的方法来求解，对于每一个玩家，计算他能否走出去。对于一些走不出去的玩家，我设定了一个步数k，每走一步k加一。如果k>150还在这个迷宫里就判定走不出去。因为这个迷宫是100个小房间，所以我就随便找了一个数150，走这么多不还没出去肯定就是走不出去啦。150设定的有点大，不过这对于计算机来说不是问题，又没有限定运行时间。

代码：

m=[['U','D','D','L','U','U','L','R','U','L'],
   ['U','U','R','L','L','L','R','R','R','U'],
   ['R','R','U','U','R','L','D','L','R','D'],
   ['R','U','D','D','D','D','U','U','U','U'],
   ['U','R','U','D','L','L','R','R','U','U'],
   ['D','U','R','L','R','L','D','L','R','L'],
   ['U','L','L','U','R','L','L','R','D','U'],
   ['R','D','L','U','L','L','R','D','D','D'],
   ['U','U','D','D','U','D','U','D','L','L'],
   ['U','L','R','D','L','U','U','R','R','R']]
count=0
for i in range(10):
    for j in range(10):
        ii=i
        jj=j
        k=0
        print((ii,jj))
        
        while k<150:
            if m[i][j]=='U':
                i=i-1
            elif m[i][j]=='D':
                i=i+1
            elif m[i][j]=='L':
                j=j-1
            else:
                j=j+1
            k=k+1
            if i<0 or i>9 or j<0 or j>9:
                count=count+1               
                break
        i=ii
        j=jj
            
        print(k)

print(count)

答案：31

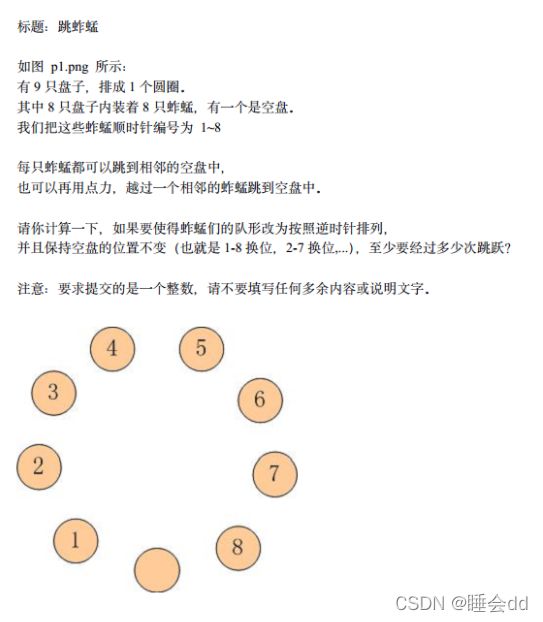
2. 跳蚱蜢

我不太会做这个，看的这个博客：

(159条消息) 蓝桥杯精选赛题——跳蚱蜢_wzyannn的博客-CSDN博客

set()集合本身有不重复性，但是这个文章里面往set()集合添加元素时还对元素进行了判重，我尝试把判重的步骤删去，结果运行时间加了好多。我觉得应该是为了加快代码运行速度才判重吧，但是set()在添加元素时本身会判重啊，我还没查到这种写法可以加快代码运行速度的文献资料。

3. 魔方状态

这个题还挺难的。。为了多刷点题这种难题先放弃

 4. 方格分割

 

方法：深度优先遍历

代码：

global ans
ans=0
map1=[[0 for i in range(7)] for j in range(7)]

direction=[(1,0),(-1,0),(0,1),(0,-1)]

def dfs(x,y):
    global ans
    if x==0 or x==6 or y==0 or y==6:
        ans=ans+1
        return
    for d in direction:
        x1=x+d[0]
        y1=y+d[1]
        if map1[x1][y1]==0:
            map1[x1][y1]=1
            map1[6-x1][6-y1]=1
            dfs(x1,y1)
            map1[x1][y1]=0
            map1[6-x1][6-y1]=0


map1[3][3]=1
dfs(3,3)
print(ans//4)

5. 正则表达式

 对于看不懂这个正则表达式的，不知道为啥题目给出的案例答案是六，看这个：

真题解析│蓝桥杯省赛真题之正则问题_括号 (sohu.com)

这个题类似的要多看看。

代码：

s=input()

count=0
pos=0
length=len(s)
def dfs():
    global length,pos
    tmp,ans=0,0
    while pos

6. 包子凑数

 

7. 等差素数序列

代码：

def sushu(n):
    nn=int(n**0.5+1)
    for i in range(2,nn):
        if n%i==0:
            return False
    return True
f=0
a=0
b=0
for i in range(2,1000):
    if sushu(n)==False:
        continue
    else:
        for j in range(1,500):
            f=0
            for r in range(i+j,i+j*11,j):
                if sushu(r)==False:
                    break
                else:
                    f=f+1
            if f==9:
                a=i
                b=j
                break
    if a!=0:
        break
if a==0:
    print("no")
else:
    print(b)