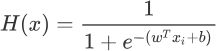机器学习 - 分类 逻辑回归 Logistic Regression（学习笔记）

逻辑回归设计思路

乍一看算法名字，会认为逻辑回归是用来解决“回归问题”的算法，但其实它是针对“分类问题”的算法。

前面我们知道，线性回归是基于样本数据拟合出一个可以预测数值的模型，从而实现了回归。而通过连续型数值获取离散型数值是很容易的，这正如水龙头喷出的水过于集中一样，只要加个转换器(花洒)就可以使水流分散输出。

19 世纪统计学家皮埃尔·弗朗索瓦·韦吕勒发明了 Logistic 函数，该函数的叫法有很多，比如在神经网络算法中被称为Sigmoid函数，也有人称它为 Logistic 曲线。该函数图像的数学表达式如下：
 

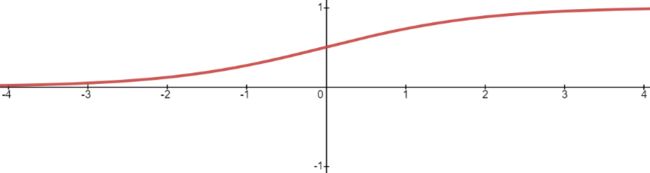
其函数图像如下所示：相当于把得分值转换成概率值。

Logistic 函数也称为 S 型生长曲线，取值范围为 (0,1)，它可以将一个实数映射到 (0,1) 的区间，非常适合做二元分类。当 z=0 时，该函数的取值为 0.5，随着 z 的增大，对应的函数值将逼近于 1；而随着 z 的减小，其函数值将逼近于 0。
对于 Logistic 函数而言，坐标轴 0 是一个有着特殊意义坐标，越靠近 0 和越远离 0 会出现两种截然不同的情况：任何大于 0.5 的数据都会被划分到 “1”类中；而小于 0.5 会被归如到 “0”类。因此可以把 Logistic 看做解决二分类问题的分类器。如果想要 Logistic 分类器预测准确，那么 x 的取值距离 0 越远越好，这样结果值才能无限逼近于 0 或者 1。 

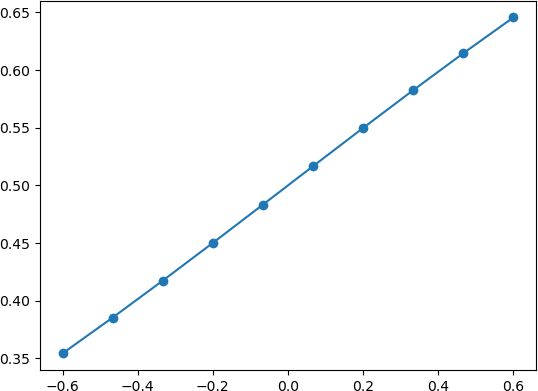
下面通过极限的思想进一步对上述函数展开研究：我们可以考虑两种情况：当 x 轴坐标取值缩小时就会出现以下图像：  

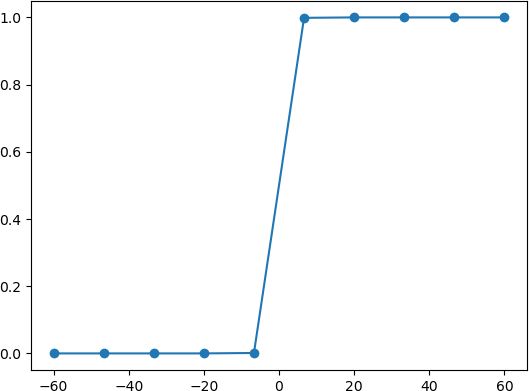
由此可见 Logistic 回归算法属于“线性”模型。而当 x 逐渐放大时则会出现以下情况：
 

由上图可知，当 x 增大到一定程度时，Logistic 函数图像变成了“台阶”式图像，由此可知，该函数能够很好的“拟合”二分类问题函数图像。在数学上，我们把具有如上图所示，这种“阶梯式”图像的函数称为“阶跃函数”。 

假设函数

损失函数

梯度上升优化方法

梯度上升与梯度下降同属于优化方法，它们两者有着异曲同工之妙，梯度下降求的是“最小值”，而梯度上升求的是“最大值”。梯度上升基于的思想是：要找到某函数的最大值，最好的发放是沿着该函数的梯度方向寻找。

多分类问题

到现在为止，逻辑回归的三大要素：模型公式、损失函数、梯度迭代已经解出，可以理解为什么把它放在分类中了。事实上，我们是通过非线性映射将回归值映射到"概率值"，但目的是实现二分类问题。那么问题来了，多分类问题该怎么办？

思路有两种：

1.这种方法各类型间不互斥，思路比较简单直接。既然你要多种的分类，多来几个转换器不就完事了吗？比如你要判别属于类1、类2还是类3，我给1、2+3来个分类，2、1+3来个分类，3、1+2来个分类，不就完事了？最后根据哪个值概率值最大，我选哪个分类就好了。

2.这种方法要求类型间互斥，被称为softmax回归。

实现Logistic回归

#从 scikit-learn库导入线性模型中的logistic回归算法
from sklearn.linear_model import LogisticRegression
#导入sklearn 中的自带数据集 鸢尾花数据集
from sklearn.datasets import load_iris
# skleran 提供的分割数据集的方法
from sklearn.model_selection import train_test_split

#载入鸢尾花数据集
iris_dataset=load_iris()

# data 数组的每一行对应一朵花，列代表每朵花的四个测量数据，分别是：花瓣的长度，宽度，花萼的长度、宽度
print("data数组类型: {}".format(type(iris_dataset['data'])))
# 前五朵花的数据
print("前五朵花数据:\n{}".format(iris_dataset['data'][:5]))

#分割数据集训练集，测试集
X_train,X_test,Y_train,Y_test=train_test_split(iris_dataset['data'],iris_dataset['target'],random_state=0)

#训练模型
#设置最大迭代次数为3000，默认为1000.不更改会出现警告提示
log_reg = LogisticRegression(max_iter=3000)
#给模型喂入数据
clm=log_reg.fit(X_train,Y_train)

#使用模型对测试集分类预测,并打印分类结果
print(clm.predict(X_test))
#最后使用性能评估器，测试模型优良，用测试集对模型进行评分
print(clm.score(X_test,Y_test))

 data数组类型:
前五朵花数据:
[[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 [4.6 3.1 1.5 0.2]
 [5.  3.6 1.4 0.2]]
[2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0
 2]
0.9736842105263158

 scikit-learn 中的 train_test_split 函数可以打乱数据集，并对其进行拆分。该函数默认将 75% 的行数据及对应标签作为训练集，另外 25% 数据作为测试集。

评估模型

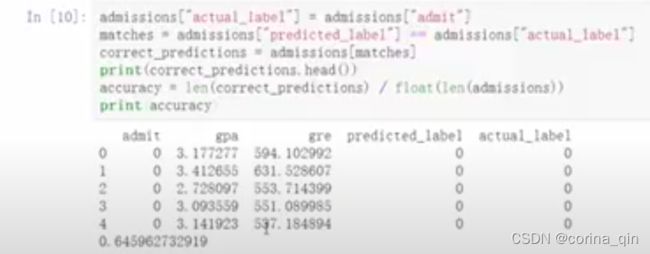
精度模型：

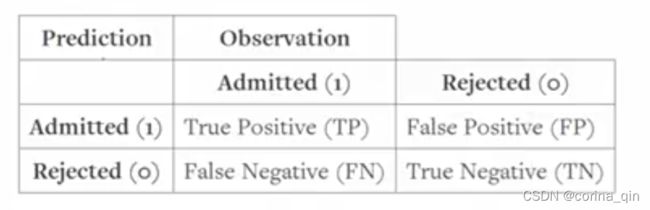
真假正负例模型：

 

True Positive Rate：模型检测正例效果如上。例如，入学问题上，true positives表示各方面优秀被录取了，false negatives表示虽然优秀但是没被录取。如果结果为12%，表明优秀的学生中只有12%被录取了，剩下的88%没被录取。正例效果太低。是否患癌问题，true positives表示患癌患者被检测出了，false negatives表示患癌患者未被检测出，这就麻烦了。

True Negative Rate：模型检测负例效果如上。例如，100个样本中，有90个属于1类别，有10个属于0类别。如果用精度预测法，在什么都不做的情况下，正确率仍有90%，所以说精度预测在样本不均条件下预测效果非常不佳。仍然是入学问题上，如果结果为96%，则表明应该入学的96%的人都确实没让入学，只有4%的漏网之鱼入学了。

总结

首先 Logistic 算法适用于分类问题，该算法在处理二分类问题上表现优越，但在多分类（二个以上）问题上容易出现欠拟合。Logistic 算法除了适用于回归分类问题，还可以作为神经网络算法的激活函数（即 Sigmoid 函数）。