【机器学习原理】KNN分类算法
上一篇：Logistic回归分类算法
文章目录
- 一、KNN分类算法：用多数表决进行分类
-
- 1. 用“同类相吸”的办法解决分类问题
-
- 可视化下的分类问题
- 2. KNN分类算法的基本方法：多数表决
- 3. 表决权问题
- 4. KNN的具体含义
- KNN分类算法原理
-
- 1. KNN分类算法的基本思路
- 2. 数学解析
- 3. KNN分类算法的具体步骤
- 三、在Python中使用KNN分类算法
- 四、KNN分类算法的使用场景
一、KNN分类算法：用多数表决进行分类
我们已经知道，Logistic回归模型虽然套着“马甲”，但核心算法仍然是线性模型，训练的方法与线性回归一样，都是首先计算出预测值与实际值的偏差，然后根据偏差来调整权值。在机器学习中，用这种通过不断减少偏差，从而实现逼近“神秘函数”的方法来训练模型的情况非常常见。但这种方法也存在一些问题，如使用梯度下降等优化方法减少偏差值时，可能出现陷入“局部最优解”的问题，导致这个问题的根本原因在于这种训练方法总是“走一步看一步”，也就是常说的“缺乏大局观”。
想要有大局观也好办，只要设计一套机器学习算法，能够先获得某种全局性的统计值，然后在全局统计值的基础上完成分类等预测工作，就可以避免陷入局部最优解了。
本章的主角KNN算法遵循这种思路，与其他分类算法相比，KNN算法的实现简单直接，与上一章的Logistic回归模型相比，第一个明显区别就在于KNN算法没有通过优化方法来不断减少偏差的显式学习过程，这意味着用不上损失函数和优化方法这套机制，在这一章可以暂且将数学放到一边。
Logistic回归的核心机制就是用损失函数和优化方法来不断调整线性函数的权值，从而拟合“神秘函数”，而偏差可谓是这套机制的动力来源。KNN算法要避免局部最优解，当然不可能再沿用这套依赖偏差的机制，但KNN作为有监督学习算法，必须设计一套参考标尺，以让标注信息发挥作用。
怎样解决这对矛盾呢？KNN算法给出的答案是“多数表决”。
- 多数表决
- 距离
1. 用“同类相吸”的办法解决分类问题
前面我们学习了用Logistic回归解决分类问题，核心思路有两条：
- 一是使用线性方程勾画直线，
- 二是通过Logistic函数把直线“掰弯”，从而拟合呈离散分布的分类问题数据点。
相当于首先通过Logistic函数把分类问题映射成回归问题，然后使用可以解决回归问题的线性模型来解决分类问题。
我们看到，有监督学习的数据集分为训练集和测试集，两种数据集的组织形式一样，但用法略有不同，训练模型一般只使用训练集，在训练集中，每条样本不但有各个维度方向对应的数值，还包括一一标注好了的分类结果。也就是说，假设当前要训练的是二元分类，那么，根据训练集“正类”和“负类”的标注结果，样本数据实际已经分成了两堆。
接下来我们要从训练集中提取分类信息，可以直接利用数据集实际已经分成两堆这个条件。想象一下，如果我们要做的不是数据分类，而是整理衣物，现在衣物已经按上衣和裤子分成了两堆，接下来你要做的就是看到上衣就扔到上衣的那一堆，看到裤子就放到裤子的那一堆。这两堆衣物就像两块大磁铁，上衣来了，就被“吸”到上衣那堆，裤子来了，就被“吸”到裤子那堆，很简单地就能完成整理工作。
分类问题的训练集是已经将样本按正负类分成了两堆，每个堆的样本都存在某种共同之处，那么，对于新输入的待分类样本究竟该归为哪一堆的问题，也就转化成新样本和哪一堆的样本共同点最多、最为相像。与哪一堆像，新样本就归为哪一堆，即分成哪一类。
可视化下的分类问题
上一章我们使用了鸢尾花的数据集演示分类，数据集中包含了三类鸢尾花，分别用三种颜色代表，取两个特征维度，绘制得到图5-1。
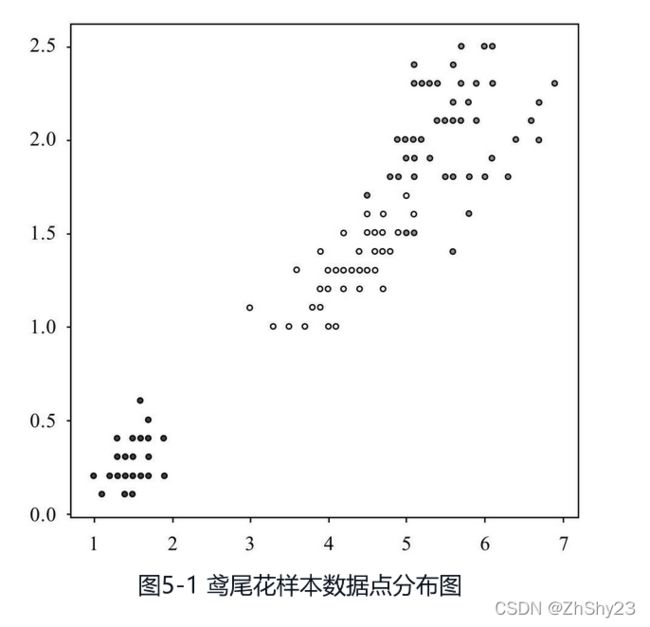
可以看出，同一类（即颜色相同）的鸢尾花样本点靠得很近，而不同类的鸢尾花样本显然离得要远一些。特征的差异形成了距离，构成了类的天然边界，客观上确实存在“同类相吸”的现象。抓住这个现象，我们就可以设置出一套新的分类方法：用已经分好类的样本作为参照，看看待分类的样本与哪一类更近，就归为哪一类。
2. KNN分类算法的基本方法：多数表决
“同类相吸”可以说是KNN分类算法的指导思想，从而机器学习模型可以脱离对偏差的依赖，而同样起到分类的效果。不过，这个想法只是KNN算法的起点，若要用来分类，许多细节问题就无法绕过。
我们知道，实际的样本是有许多维度的，如鸢尾花数据集，虽然它是一个非常小的数据集，但每个鸢尾花样本也包含了花萼的长度、宽度和花瓣的长度、宽度4个维度，从不同维度看，样本数据点的分布情况不相同。假设每次任意取鸢尾花数据集4个维度中的2个，分别作为图像的X轴和Y轴坐标，将得到16张图像。除了图5-1，这里再另外选取4张不同维度所绘制的图像，可以比较观察不同维度下样本点的分布变化（见图5-2）。
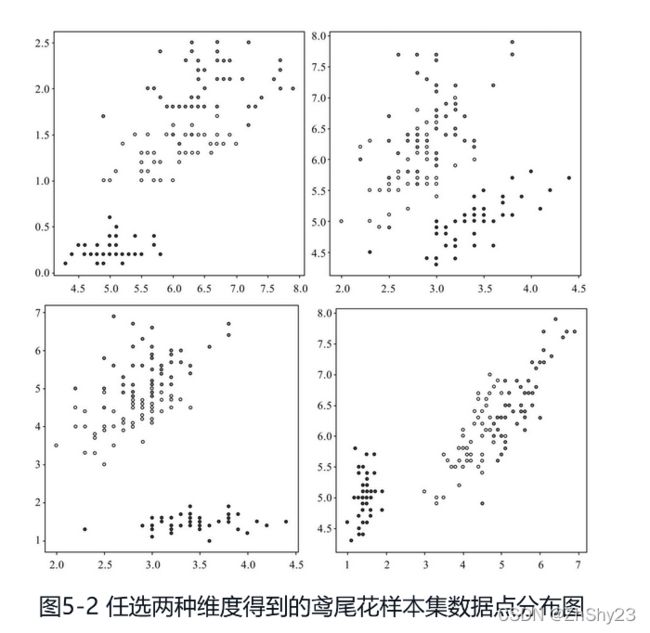
可以看出，对于同样的样本，选取不同的维度之后，类与类之间呈现出了犬牙交错的更为复杂的关系，而同一类的“聚集”趋势也变得不太明显，类内样本的分布范围更广，与其他类的样本混杂在一起的可能性变得更大。
如何选取维度是KNN算法乃至机器学习都需要重点关注的问题，选取合适的维度可以事半功倍。
不同的维度选择可能导致样本呈现不同的分布情况。虽然我们可以人为挑选几个维度，让相同种类的鸢尾花数据点在分布上靠得更近，但这就成了“先有结论再找证据”，刻意成分太多，需要事先通过人工来分析究竟哪些维度能起到良好效果，而且相关维度超过3个之后还存在无法可视化的问题，所以需要想办法让模型能够自行完成这个过程。
不同的机器学习算法对于维度的选取有着不同的办法，Logistic回归算法采用“加权”的办法，让做出正面贡献的维度输入增加权值，而KNN算法则选择了更为直接和“文艺”的方法：多数表决。
物以类聚，人以群分，你是哪一类人，查查你的朋友圈也许就能知道答案。KNN分类算法所采用的方法同样也是“查朋友圈”。前面我们说过，训练集的样本已经按正负类分好了，现在过来一个待分类的新样本，只需要查一查“朋友圈”，也就是根据它各个维度的值，看看与它临近的点都是什么类，按多数表决原则，哪些类占大多数，这个新样本就属于哪一类。
3. 表决权问题
分类问题的训练集样本可没有什么朋友圈，需要我们设计一个方法来划定这个“圈”。对于KNN，这个圈就是由距离决定的。具体来说，根据样本各个维度的值可以作出一个个数据点，我们只需要度量点与点之间的距离，然后若想给某个点划分“朋友圈”，只需要以这个点为圆心，就可以找到与它临近的点有哪些，从而构成它的“朋友圈”。只有在圈子里的点才拥有对于这个点属于哪个类的表决权，而不是由全体样本进行表决。这是一个需要注意的细节。
为什么不用全体样本表决呢？如果采用这种方法，那么新加入样本的类别一定就是原来在全体样本中占大多数的类别，这个类别是正类还是负类，主要受样本采集方法的影响，与分类的本身关系不大。随着新样本的不断加入，这个类别在全体样本中的占比也将不断扩大，使得新加入样本始终都是这个类别，从而形成“滚雪球”效应，也就无法起到分类的作用了。
再说说距离度量。在二维平面上，我们习惯用直尺来测量距离，所以也没有觉得这有难度。但是，数据点常常有多个维度，如鸢尾花的数据点就有4个维度，这就没法直接用尺子量了。怎么办呢？数学家已经为我们准备好了多种衡量距离的数学工具，根据需要选取其中一种，同样可以确定点与点之间的距离，以及指定的点与谁临近。至于为什么用距离确定“朋友圈”，其实也好理解，走得近的当然才称得上朋友嘛！
4. KNN的具体含义
KNN是K-Nearest Neighbor的英文简写，中文直译就是K个最近邻，有人干脆称之为“最近邻算法”。字母“K”也许看着新鲜，不过作用其实早在中学就接触过。在学习排列组合时，教材都喜欢用字母“n”来指代多个，譬如“求n个数的和”，这里面也没有什么秘密，就是约定俗成的用法。而KNN算法的字母K扮演的就是与n同样的角色。K的值是多少，就代表使用了多少个最近邻。机器学习总要有自己的约定俗成，没来由地就是喜爱用“K”而不是“n”来指代多个，类似的命名方法还有后面将要提到的K-means算法。
KNN的关键在于最近邻，光看名字似乎与分类没有什么关系，但前面我们介绍了， KNN的核心在于多数表决，而谁有投票表决权呢？就是这个“最近邻”，也就是以待分类样本点为中心，距离最近的K个点。这K个点中什么类别的占比最多，待分类样本点就属于什么类别。
KNN分类算法原理
1. KNN分类算法的基本思路
作为一种分类算法，KNN最核心的功能“分类”是通过多数表决来完成的，具体方法是在待分类点的K个最近邻中查看哪个类别占比最多。哪个类别多，待分类点就属于哪个类别。
KNN算法负责实现分类的部分简单直接，但容易让人产生疑惑的两点正出自它的名字：
- 一是怎样确定“K”，
- 二是怎样确定“NN”。
投票表决的流程清晰明了，但谁拥有投票表决权却是使用KNN算法时首先需要解决的问题。
在使用机器学习算法模型解决实际问题时，给模型调参数是继数据清洗之后的又一重要工作，需要时间和经验。调参工作所需要花费的时间和得到的效果，正是新手和老手的重要差别之一。在KNN算法中，将K值设置为多少没有具体的计算公式，只能根据各位的实战经验确定了。
不同的算法模型可调的参数是不一样的。在KNN算法中，“KNN”中的这个“K”——也就是该选几个点，就是一个需要根据实际情况调节以便取得更好拟合效果的参数，可以根据交叉验证等实验方法，结合工作经验进行设置，一般情况下，K的值会在3～10之间。
“最近邻”初看已经把要求都说明白了，但仔细一想就能发现其中空间很大。KNN算法已经衍生出很多变种，用什么方法度量“最近”，正是KNN以及相关衍生算法需要解决的首要问题，是难点，也是创新点。
前面我们在介绍L2范式时提到的欧几里得距离，就是KNN中常用的度量方法，但这不是唯一的度量方法。通过选择不同的距离度量方法，同样的KNN算法能够有完全不同的表现。如果你计划为KNN设计一种变种，“最近邻”就是你应该开始着手的地方。
假设已经有5个样本点，用颜色代表类别，现在放入一个新的待分类样本，由于类别不明，颜色用白色表示（见图5-3）。
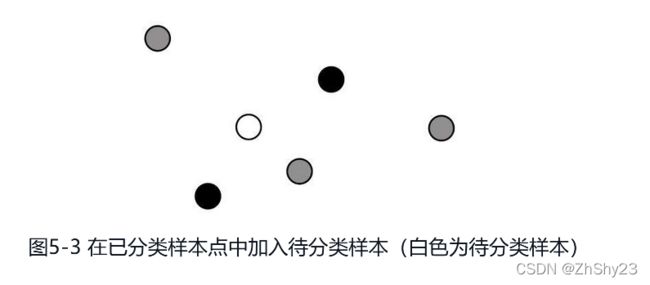
首先逐一确定待分类样本点和训练集样本点的距离，见图5-4。
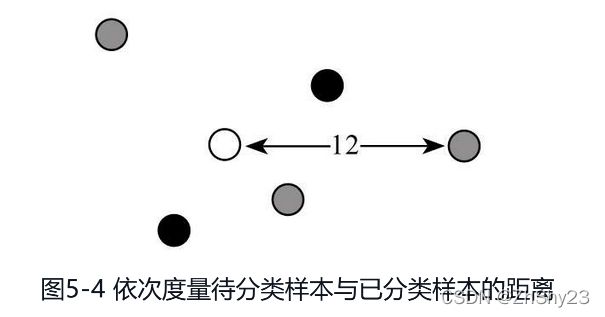根据距离圈定表决范围，见图5-5。
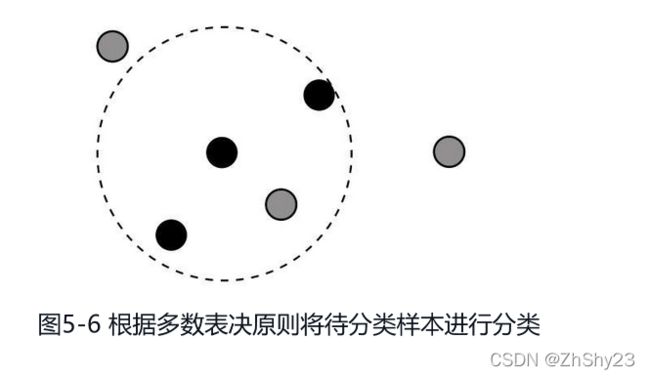
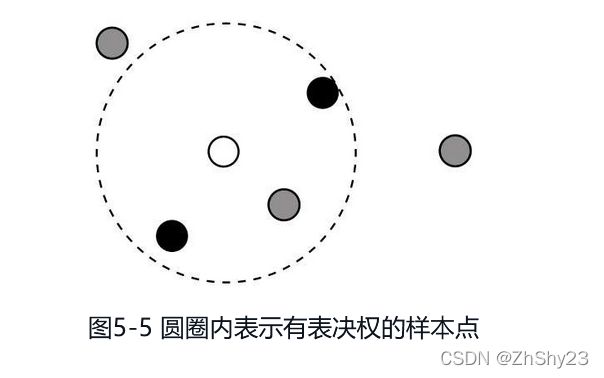根据多数表决原则，决定待分类样本点的类别，由于黑色占大多数，所以待分类样本也为黑色，见图5-6。
2. 数学解析
首先是上文提到的闵可夫斯基距离，虽然它的名字包含“距离”，但实际上是对一类距离的统一定义。闵可夫斯基距离的数学表达式如下：
d p ( x , y ) = ( ∑ i = 1 n ∣ x i − y i ∣ p ) 1 / p (5-1) d_p(x,y)=\left(\sum^n_{i=1}|x_i-y_i|^p\right)^{1/p} \tag{5-1} dp(x,y)=(i=1∑n∣xi−yi∣p)1/p(5-1)
闵可夫斯基距离是一组距离的定义，不妨把闵可夫斯基距离看作一个代数形式的母版，通过给P设置不同的值，就能用闵可夫斯基距离得到不同的距离表达式。
-
当p=1时，称为曼哈顿距离：
d ( x , y ) = ∑ k = 1 n ∣ x k − y k ∣ (5-2) d(x,y)=\sum^n_{k=1}|x_k-y_k| \tag{5-2} d(x,y)=k=1∑n∣xk−yk∣(5-2)
据说曼哈顿距离最初是用于度量美国曼哈顿市出租车的行驶距离，不妨把曼哈顿市的地图看作围棋的棋盘，出租车只能沿着棋盘上的横线和纵线行驶，出租车从一个地点到另一个地点的行驶轨迹就是曼哈顿距离。也许光看曼哈顿距离的表达式不够直观，我们以计算图5-7中A点到坐标原点的曼哈顿距离为例进行说明。
图5-7中A点坐标为（3,2），即x1为3,y1为2。原点坐标为（0,0），即x2为0， y2为0。根据曼哈顿距离计算公式：
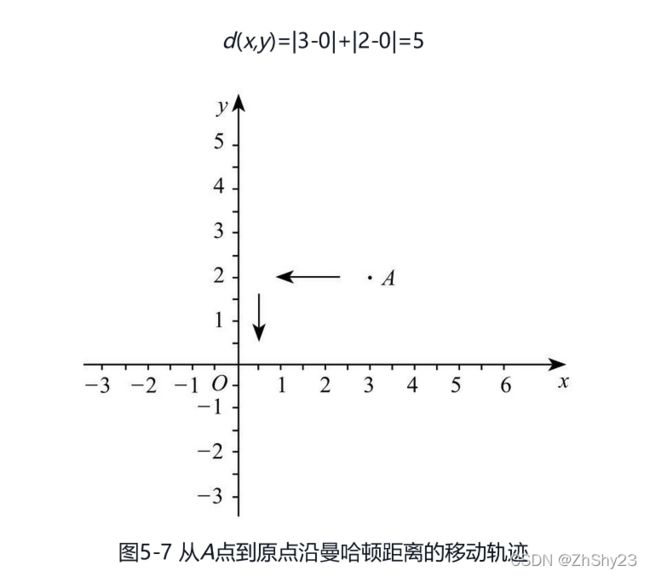其实可以看作A点到原点移动了两次，第一次是从（3,2）沿着直线移动到（0,2），第二次再从（0,2）沿着直线移动到（0,0）。两次移动距离的和就是曼哈顿距离。 -
当p=2时，为欧几里得距离，最常用于度量两点之间的直线距离，表达式和L2范式是一样的，具体如下：
d 2 ( x , y ) = ∑ i = 1 n ( x i − y i ) 2 (5-3) d_2(x,y)=\sqrt{\sum^n_{i=1}(x_i-y_i)^2} \tag{5-3} d2(x,y)=i=1∑n(xi−yi)2(5-3)
距离的度量方法没有好坏，选择什么方法主要是根据当前情况而定。如果其他样本点呈圆形分布，而待分类点正好处于圆心，这种情况下由于到各个点的欧式距离都一样，也就无法使用欧式距离进行选择。曼哈顿距离相当于“数格子”，相比之下具有更高的稳定性，但同样存在丢失距离信息的问题，最终还是需要根据实际情况进行选择。
3. KNN分类算法的具体步骤
KNN算法是一种有监督的分类算法，输入同样为样本特征值向量以及对应的类标签，输出则为具有分类功能的模型，能够根据输入的特征值预测分类结果。具体如表5-1所示。
KNN分类算法的思路很简洁，实现也很简洁，具体分三步：
- 找K个最近邻。KNN分类算法的核心就是找最近的K个点，选定度量距离的方法之后，以待分类样本点为中心，分别测量它到其他点的距离，找出其中的距离最近的“TOP K”，这就是K个最近邻。
- 统计最近邻的类别占比。确定了最近邻之后，统计出每种类别在最近邻中的占比。
- 选取占比最多的类别作为待分类样本的类别。
三、在Python中使用KNN分类算法
neighbors类库：
KNeighborsClassifier类：最经典的KNN分类算法。KNeighborsRegressor类：利用KNN算法解决回归问题。RadiusNeighborsClassifier：基于固定半径来查找最近邻的分类算法。NearestNeighbors类：基于无监督学习实现KNN算法。KDTree类：无监督学习下基于KDTree来查找最近邻的分类算法。BallTree类：无监督学习下基于BallTree来查找最近邻的分类算法。
本章所介绍的KNN分类算法可以通过KNeighborsClassifier类调用，用法如下：
from sklearn.datasets import load_iris
# 从scikit-learn库导入近邻模型中的KNN分类算法
from sklearn.neighbors import KNeighborsClassifier
# 载入鸢尾花数据集
X, y = load_iris(return_X_y=True)
# 训练模型
clf = KNeighborsClassifier().fit(X, y)
# 使用模型进行分类预测
print("array({})".format(clf.predict(X)))
==========================================
array([0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1
1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 1 2 2 2 2
2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2])
使用默认的性能评估器评分：
print("score: {}".format(clf.score(X, y)))
==============================
score: 0.9666666666666667
四、KNN分类算法的使用场景
算法使用案例
OCR（Optical Character Recognition，光学字符识别）是一种常用的功能，如拍照搜题的原理就是首先对题目进行拍照，然后用OCR识别出照片中的符号和文字，最后才在题库中进行搜索和呈现结果。其他常见的OCR应用还包括手写数字识别和PDF转Word文档。如今OCR通常使用深度神经网络来实现，但在深度学习兴起之前，OCR一般是通过KNN和后面即将介绍的支持向量机两种算法实现。用KNN实现OCR主要分为三步：第一步确定文字所在位置区域，第二步提取特征，第三步通过KNN最近邻分类算法，判断所提取的相关特征属于哪个字符。