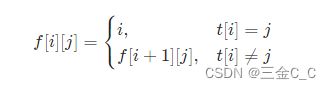[算法周训 2]字符串训练1

本周算法周训练习二，依旧是在Leetcode平台进行刷题。本周的题目大多集中在字符串处理上面，很多题目也都是使用到了哈希表（Map)的解法，这让我的算法又进一步得到了锻炼。

同时也借助题目（重复的子字符串）复习了KMP算法，相关知识笔记点击此处不过方便的可以直接使用C++ 中的find函数，也不用自己来写了，当然这个也确实不是KMP，而是朴素算法。这里也讲到了循环可以快慢指针来进行遍历；另外还有回溯算法的标准模板式。

以下题目算是对字符串的阶段性的刷题训练。当然了，这也是我平时抽时间写的了。如果后面有时间的话，我将带来专题训练以此巩固。

组合总和

这个题目很明显就是深搜模板题了，为什么这么说呢？可以看示例1,输出的2出现了很多次，也就是类似于图论的一直走，当出现后面的数加上前面的数大于target就退出递归上层（俗称剪枝操作）。那么这个题目思路是有了。
这个题目完全可以把思路背下来当做模板来背，非常常见的dfs与剪枝操作。

class Solution {
public:

    vector<vector<int>> az;
    vector<int> tmp;

    void dfs(vector<int> & a, int sum,int target,int index) {
        if( sum == target ) {
            az.push_back(tmp);
            return;
        }
        for(int i= index;i<a.size();i++) {
            if(a[i] > target || a[i] + sum > target) {
                break;
            }
            tmp.push_back(a[i]);
            sum += a[i];
            dfs(a,sum,target,i);
            tmp.pop_back();
            sum -= a[i];
        }
    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
    sort(candidates.begin(),candidates.end());
    dfs(candidates,0,target,0);
    return az;
    }
};

快乐数

个人觉得这是简单题。主要关注的是无限循环。很明显，无限循环的必要条件肯定是会形成环。我一开始是觉得这个环可以到数组0位，后面仔细思考，这个循环的环头可以是从数组开始的任意一位，所以这就需要我们，将得出结果n保存在一个数组中，后面算的时候倘若出现又出现了n那么必定是false,否则就将会得到1.

首先是老规矩的算各位和。后面就是简单的放进数组了，当然这里可以使用大数组来牺牲空间保证时间速度。（这个保存数组最多到1000位，想想为什么呢？）

class Solution {
public:

    int fun(int n) {
        int sum = 0;
        while(n) {
            int x = n % 10;
            sum += x*x;
            n /= 10;
        }
        return sum;
    }
   vector<int> a;
    bool isHappy(int n) {
    a.push_back(n);
    int tmp = n;
    while(1) {
        int s = tmp;
        int t = fun(s);
        a.push_back(t);
        if(t == 1) return true;
        tmp = t;
        
        for(int i=0;i<a.size()-1;i++) {
            if(t == a[i]) return false;
        }
    }
}
};

还有一种办法就是双指针：
这也是判断循环的一个方法：

// 和上面的fun一样功能
bool isHappy(int n) 
{
	int slow = n,fast = n;
	do{
	`	slow = fun(slow);
		fast = fun(fast);
		fast = fun(fast);
	}while(slow != fast);
	return slow == 1;
}

字符串中的第一个唯一字符

注意关键词：不重复。想什么呢？那当然是map了，一个是map用来保存字符的次数。这个题目我一开始做烦了，使用两个map一个用来保存次数一个用来保存索引。

class Solution {
public:
    map<char,int> a;
    int m[26];
    int c[26];
    int firstUniqChar(string s) {
        memset(m,0,sizeof(m));
        memset(c,-1,sizeof(c));
        for(int i=0;i<s.size();i++) {
            if(a.find(s[i]) == a.end()) {
                a.insert(pair<char,int>(s[i],1));
                m[s[i]-'a'] = i;
            }else {
                a[s[i]] ++;
            }
        }
        map<char,int> ::iterator it = a.begin();
        for(;it != a.end();++it) {
            if(it->second == 1) {
                c[it->first - 'a'] = m[it->first - 'a'];
            }
        }
        sort(c,c+26);
        for(int i = 0;i<26;i++) {
            if(c[i]!= -1) return c[i];
        }
        return -1;
    }
};

其实个人觉得map这里显得多余了，不过嘛，作为次数的通用使用map还是不错的。
所以提供一个不错的写法吧：

class Solution {
public:
    int firstUniqChar(string s) {
        int m[26] = {0};
        for(auto e:s) m[e-'a'] ++;
        for(int i=0;i<s.length();++i){
			if(m[s[i]-'a'] == 1) return i;
		}
    }
    return -1;
};

找不同

和上面那个题目实在太像了：只要计算两个s，t的次数就可以了。

class Solution {
public:
    char findTheDifference(string s, string t) {
        int a[26],b[26];
        memset(a,0,sizeof(a));
        memset(b,0,sizeof(b));
        for(int i=0;i<s.length();i++) {
            a[s[i]-'a'] ++;
            b[t[i]-'a'] ++;
        }
        b[t[s.length()] - 'a'] ++;
        for(int i=0;i<26;i++) {
            if(a[i] != b[i]) return i+'a';
        }
        return ' ';
    }
};

哦对了，这个还有位操作，相当不错的解法：
**如果将两个字符串拼接成一个字符串，则问题转换成求字符串中出现奇数次的字符。**注意位运算可以解决奇数次问题。

class Solution {
public:
    char findTheDifference(string s, string t) {
        int ret = 0;
        for (char ch: s) {
            ret ^= ch;
        }
        for (char ch: t) {
            ret ^= ch;
        }
        return ret;
    }
};

重复的子字符串

我的想法很简单，就是简单暴力（当然了，暴力是从索引1开始，然后逐个加字符串进行比较的，为什么呢，因为子字符串肯定要包含第一索引位的哦）当然了，一想到匹配，很明显的 KMP风格了。

class Solution {
public:
    bool repeatedSubstringPattern(string s) {
        int n = s.size();
        if( n == 2) {
            if(s[0] != s[1]) return false;
            else return true;
        }
        for(int i=1;i<=n/2;i++) {
            string m = s.substr(0,i);
            if( n % m.size() != 0 ) continue;
            for(int j = i ;j<=n-1;j += i) {
                string c = s.substr(j,m.size());
                if( c != m ) goto here;
            }
            return true;
            here:
            continue;
        }
        return false;
    }
};

方法二：假设字符串s可由一个子串x重复n次构成，即s = nx。现在构造新字符串t = 2s=2nx. 去掉t的开头与结尾两位，则这两处的子串被破坏掉，此时t中包含2n-2个子串。 由于t中包含2n-2个子串，s中包含n个子串，若t中包含s，则有2n-2>=n，可得n>=2，由此我们可知字符串s可由一个子串x重复至少2次构成，判定为true；反之，若t中不包含s，则有2n-2 相关的kmp算法不再介绍了，直接使用STL中的find函数了（主要是考场时候也很难写出来）

bool repeatedSubstringPattern(string s) {
        string str=s+s;
        str=str.substr(1,str.size()-2);
        if(str.find(s)==-1)
            return false;
        return true;
    }

同构字符串

注意到映射的关键词，很显然，2个map可以解决：

class Solution {
public:

    map<char,char> mac;
    map<char,char> ma;
    bool isIsomorphic(string s, string t) {
        int a=s.size(),b = t.size();
        if(a != b) return false;
        for(int  i = 0;i<a;i++) {
            if( mac.find(s[i]) == mac.end()) {
                mac.insert(pair<char,char>(s[i],t[i]));
            }else {
                if( mac[s[i]] != t[i]) return false;
            }
        }

        for(int  i = 0;i<a;i++) {
            if( ma.find(t[i]) == ma.end()) {
                ma.insert(pair<char,char>(t[i],s[i]));
            }else {
                if( ma[t[i]] != s[i]) return false;
            }
        }

        return true;
    }
};

当然了，还有简单的办法，只要遍历就行。

class Solution {
    public boolean isIsomorphic(String s, String t) {
          for(int i = 0; i < s.length(); i++){
              if(s.indexOf(s.charAt(i)) != t.indexOf(t.charAt(i))){
                  return false;
              }
          }  
          return true;
    }
}

判断子序列

这个题目也很显然啊，不要想复杂了，我一开始就做得很麻烦（就是遍历s,t然后s的字符串没有的就在t中删除，最后再比较，但这样出现一些问题）
这个题目也比较简单，也是遍历。贪心发现匹配靠前的字符是满足题意的

class Solution {
public:
    bool isSubsequence(string s, string t) {
        int i = 0;
        for(int j=0;i<s.size()&&j<t.size();j++) {
            if(s[i] == t[j]) {
                i++;
            }
        }
        return i == s.size();
    }
};

方法二就是动态规划，其实这个子序列使用dp还是很常见的了。（抽时间我一定要完成背包问题九讲内容）
令f[i][j]表示字符串t从i开始往后字符j第一次出现的位置。如果t中位置i的字符就是j，那么f[i][j] = i,否则j出现在位置i+开始往后，即f[i][j]=f[i+1][j]。状态方程如下：

class Solution {
public:
    bool isSubsequence(string s, string t) {
        int n = s.size(), m = t.size();

        vector<vector<int> > f(m + 1, vector<int>(26, 0));
        for (int i = 0; i < 26; i++) {
            f[m][i] = m;
        }

        for (int i = m - 1; i >= 0; i--) {
            for (int j = 0; j < 26; j++) {
                if (t[i] == j + 'a')
                    f[i][j] = i;
                else
                    f[i][j] = f[i + 1][j];
            }
        }
        int add = 0;
        for (int i = 0; i < n; i++) {
            if (f[add][s[i] - 'a'] == m) {
                return false;
            }
            add = f[add][s[i] - 'a'] + 1;
        }
        return true;
    }
};

字符串相加

别的不说，大数模板题目：注意的是从字符串最后开始遍历，需要进位符

class Solution {
public:
    string addStrings(string num1, string num2) {
        string str = "";
        int cur = 0,i = num1.size()-1, j = num2.size()-1;
        while( i >= 0 || j >= 0 || cur != 0) {
            if(i >= 0) cur += num1[i--] - '0';
            if(j >= 0 ) cur += num2[j--] -'0';
            str += to_string( cur % 10);
            cur /= 10;
        }
        reverse(str.begin(),str.end());
        return str;
    }
};

数组的度

这个题目我使用了暴力解决，当然，最后还是超时了，先说一下我的方法，就是简单的模拟，先找出谁是数组的度的数（注意这里的数不止一个，所以我这里使用了vector进行保存），然后又是n方遍历了

class Solution {
public:
    static bool cmp(int a,int b) {
        return a>b;
    }
    map<int,int> a;
    int findShortestSubArray(vector<int>& nums) {
        for(int i=0;i<nums.size();i++) {
            if(a.find(nums[i]) == a.end()) {
                a.insert(pair<int,int>(nums[i],1));
            }else{
                a[nums[i]] ++;
            }
        }
        int max = -1;
        vector<int > b;
        vector<int> count;
        map<int,int> ::iterator it = a.begin();
        for(;it!=a.end();++it) {
            int x = it->first;
            int y = it->second;
            count.push_back(y);
        }
        sort(count.begin(),count.end(),cmp);
        map<int,int> ::iterator itc = a.begin();
        for(;itc!=a.end();++itc) {
            int x = itc->first;
            int y = itc->second;
            if(y == count[0]) {
                b.push_back(x);
            }
        }
        int maxc = 99999999;
        //cout<
        //for(int i=0;i
        for(int j=0;j<b.size();j++) {
            int count = 0;
            int be,end;
            for(int i=0;i<nums.size();i++) {
                
                if(nums[i] == b[j] && count < a[b[j]]) {
                    if(count == 0) {
                        be = i;
                        //cout<
                    }
                    count ++;
                }
                if(count == a[b[j]]) {end = i;
               // cout<
                int len = end -be;
                if(maxc > len ) {
                    maxc = len;
                }}
            }
        }
        return maxc+1;
    }
};

这个题目我个人觉得还是有点挑战性的，如果考虑时间限制的话（单纯地暴力模拟是没什么问题）
我们需要做的是，满足条件的x有很多，所以需要统计每个数的次数，同时也得统计每个数的第一次出现和最后一次出现。其实看到这里的时候很明显我是想用一个struct来保存信息的，但是给我一个困难是，如何确定最后一次出现呢。
第一次更新很好确定，最后一次出现，答案就是更新，不断地更新。
说白了就是我上面的缩减版，总体思路是一样的，只不过我的一些信息并没有处理到位。

class Solution {
public:
    map<int,int> a;
    map<int,int> b;
    map<int,int> c;
    int findShortestSubArray(vector<int>& nums) {
        int de =0;
        for(int i=0;i<nums.size();i++) {
            if(a.find(nums[i]) == a.end()) a[nums[i]] = i;
            b[nums[i]] = i;
            c[nums[i]] ++;
            de = max(de,c[nums[i]]);
        }
        int re=nums.size() ;
        for( auto& k: c) {
            if(k.second == de) {
                re  = min(re,b[k.first]-a[k.first]+1);
            }
        }
        return re;
    }
};