分组卷积/转置卷积/空洞卷积/反卷积/可变形卷积/深度可分离卷积/DW卷积/Ghost卷积/

---

1. 常规卷积

假设输入层为一个大小为$64\times 64$像素、三通道彩色图片。经过一个包含$4$个Filter的卷积层，最终输出$4$个Feature Map，且尺寸与输入层相同。整个过程可以用下图来概括。

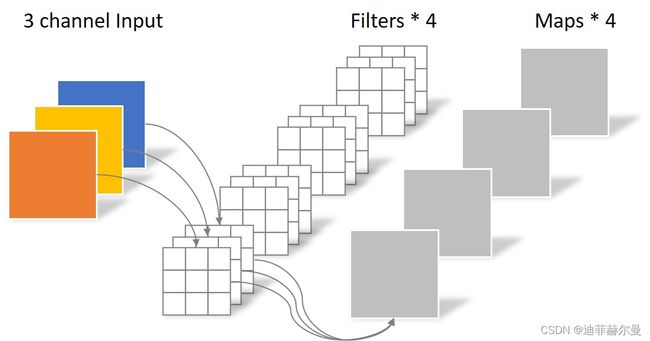
参数量计算，bias忽略不计
N = 4 × 3 × 3 × 3 = 108

---

2. 分组卷积

分组卷积就是将输入通道和输出通道都划分为同样的组数，然后仅让处于相同组号的输入通道和输出通道相互进行“全连接”，如下图所示，如记$g$为输入/输出通道所分的组数，则分组卷积能够将卷积操作的参数量和计算量都降低为普通卷积的$1/g$

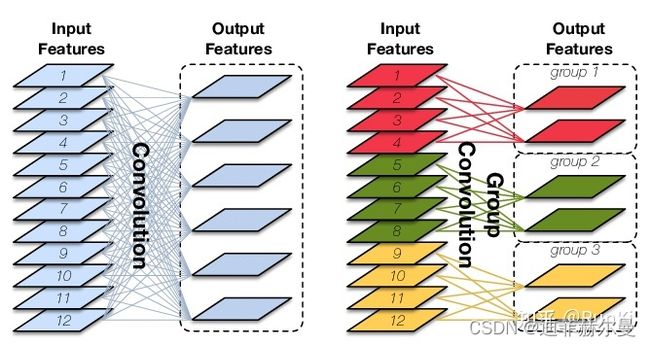
分组卷积最初是在AlexNet网络中引入的。当时是为了解决单个GPU无法处理含有较大计算量和存储需求的卷积层问题。目前随着硬件设备的不断升级，分组卷积多被用于移动设备的小型网络模型。

虽然在理论上它可以显著降低计算量和参数量，但是对内存的访问频繁程度并未降低，且现有GPU加速库对其优化程度有限，因此在效率上提升并不显著。

参数量对比
N = 12 × 6 × 3 × 3 = 648
N_group = 4 × 2 × 3 × 3 + 4 × 2 × 3 × 3 + 4 × 2 × 3 × 3 = 216

---

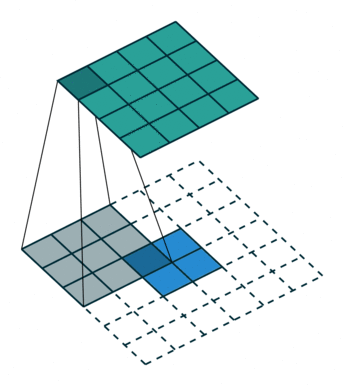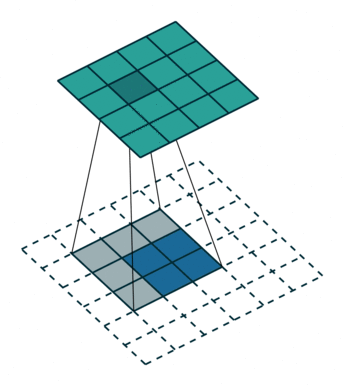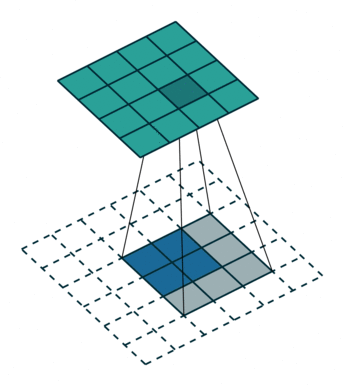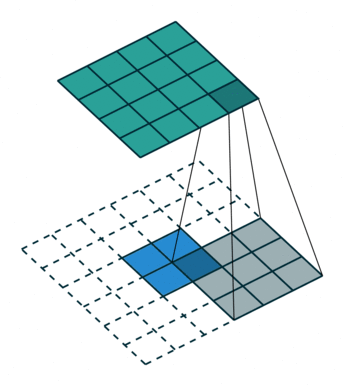
3. 转置卷积

转置卷积也被称为反卷积(deconvolution)，它可以看作是普通卷积的一个“对称”操作，这种“对称性体现在以下两个方面”：

• 转置卷积能将普通卷积中输入到输出的尺寸变换逆反过来，这里需要注意的是，输入特称图经过普通卷积操作后再经过转置卷积，只是恢复了形状，并不能复原具体的取值
• 转置卷积的信息正向传播于普通卷积的误差反向传播所用的矩阵相同，反之亦然

普通卷积和转置卷积所处理的基本任务是不同的。前者主要用来做特征提取，倾向于压缩特征图尺寸；后者主要用于对特征图进行扩张或上采样，代表性的场景如下：

• 语义分割/实例分割
• 一些物体检测、关键点检测
• 图像的自编码器、变分自编码器、生成对抗网络等

---

4. 空洞卷积

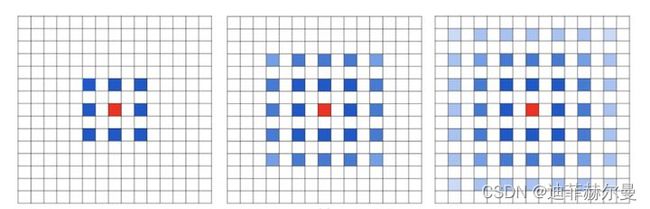
空洞卷积是针对图像语义分割问题中下采样会降低图像分辨率、丢失信息而提出的一种卷积思路。利用添加空洞扩大感受野，让原本3x3的卷积核，在相同参数量和计算量下拥有5x5（dilated rate =2）或者更大的感受野，从而无需下采样。

扩张卷积（dilated convolutions）又名空洞卷积（atrous convolutions），向卷积层引入了一个称为 “扩张率(dilation rate)”的新参数，该参数定义了卷积核处理数据时各值的间距。换句话说，相比原来的标准卷积，扩张卷积（dilated convolution） 多了一个hyper-parameter（超参数）称之为dilation rate（扩张率），指的是kernel各点之前的间隔数量，正常的convolution 的 dilatation rate为 1

空洞卷积优点

• 在不做pooling损失信息和相同的计算条件下的情况下，加大了感受野，让每个卷积输出都包含较大范围的信息。空洞卷积经常用在实时图像分割中。当网络层需要较大的感受野，但计算资源有限而无法提高卷积核数量或大小时，可以考虑空洞卷积。

空洞卷积缺点

• Dilated Convolution的kernel并不连续，也就是并不是所有的像素都用来计算了，因此这里将信息看作checker-board的方式将会损失信息的连续性。(即栅格效应，膨胀卷积不能覆盖所有的图像特征，如下图所示）

• Dilated Convolution的设计更像是用于获取long-range information，这样或许对一些大物体有较好的分隔效果，而对于小物体来说可能是有弊无利了。如何同时处理好大小物体的关系，则是设计好dilated convolution网络的关键

---

5. 可变形卷积

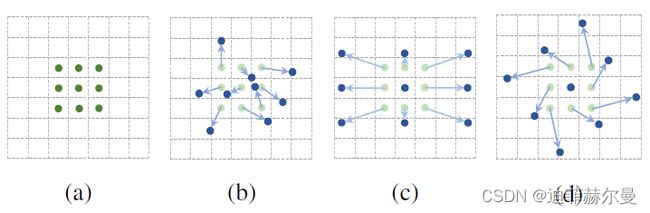
普通卷积操作在固定的、规则的网格点上进行数据采样，这束缚了网络感受野形状，限制了网络对几何形变的适应能力。为了克服这个限制，可变形卷积在卷积核的每个采样点上添加一个可学习的偏移量(offset)，让采样点不再局限于规则的网格点，

可变性卷积的流程为：

• 原始图片batch（大小为b*h*w*c），记为U，经过一个普通卷积，卷积填充为same，即输出输入大小不变，对应的输出结果为（b*h*w*2c)，记为V，输出的结果是指原图片batch中每个像素的偏移量（x偏移与y偏移，因此为2c）。
• 将U中图片的像素索引值与V相加，得到偏移后的position（即在原始图片U中的坐标值），需要将position值限定为图片大小以内。position的大小为（b*h*w*2c)，但position只是一个坐标值，而且还是float类型的，我们需要这些float类型的坐标值获取像素。
• 例，取一个坐标值（a,b)，将其转换为四个整数，floor(a), ceil(a), floor(b),ceil(b)，将这四个整数进行整合，得到四对坐标(floor(a),floor(b)),((floor(a),ceil(b)), ((ceil(a),floor(b)),((ceil(a),ceil(b))。这四对坐标每个坐标都对应U中的一个像素值，而我们需要得到(a,b)的像素值，这里采用双线性差值的方式计算（一方面得到的像素准确，另一方面可以进行反向传播）。
• 在得到position的所有像素后，即得到了一个新图片M，将这个新图片M作为输入数据输入到别的层中，如普通卷积。

---

6. 深度可分离卷积(Separable Convolution)

Separable Convolution在Google的Xception以及MobileNet论文中均有描述。它的核心思想是将一个完整的卷积运算分解为两步进行，分别为Depthwise Convolution与Pointwise Convolution。

6.1 Depthwise Convolution

同样是上述例子，一个大小为64×64像素、三通道彩色图片首先经过第一次卷积运算，不同之处在于此次的卷积完全是在二维平面内进行，且Filter的数量与上一层的Depth相同。所以一个三通道的图像经过运算后生成了3个Feature map，如下图所示。

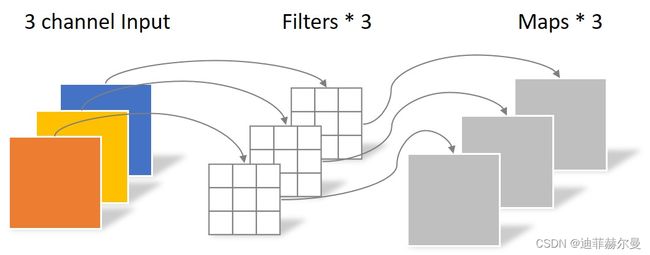
其中一个Filter只包含一个大小为3×3的Kernel，卷积部分的参数个数计算如下：

N_depthwise = 3 × 3 × 3 = 27

Depthwise Convolution完成后的Feature map数量与输入层的depth相同，但是这种运算对输入层的每个channel独立进行卷积运算后就结束了，没有有效的利用不同map在相同空间位置上的信息。因此需要增加另外一步操作来将这些map进行组合生成新的Feature map，即接下来的Pointwise Convolution。

6.2 Pointwise Convolution

Pointwise Convolution的运算与常规卷积运算非常相似，不同之处在于卷积核的尺寸为 1×1×M，M为上一层的depth。所以这里的卷积运算会将上一步的map在深度方向上进行加权组合，生成新的Feature map。有几个Filter就有几个Feature map。如下图所示。

由于采用的是1×1卷积的方式，此步中卷积涉及到的参数个数可以计算为：

N_pointwise = 1 × 1 × 3 × 4 = 12

经过Pointwise Convolution之后，同样输出了4张Feature map，与常规卷积的输出维度相同。

参数对比

回顾一下，常规卷积的参数个数为：

N = 4 × 3 × 3 × 3 = 108

Separable Convolution的参数由两部分相加得到：

N_depthwise = 3 × 3 × 3 = 27
N_pointwise = 1 × 1 × 3 × 4 = 12
N_separable = N_depthwise + N_pointwise = 39

相同的输入，同样是得到4张Feature map，Separable Convolution的参数个数是常规卷积的约1/3。因此，在参数量相同的前提下，采用Separable Convolution的神经网络层数可以做的更深。

---

7. Ghost卷积

来自华为诺亚方舟实验室，发表于2020年的CVPR上。提供了一个全新的Ghost模块，旨在通过廉价操作生成更多的特征图。其原理如下图所示。

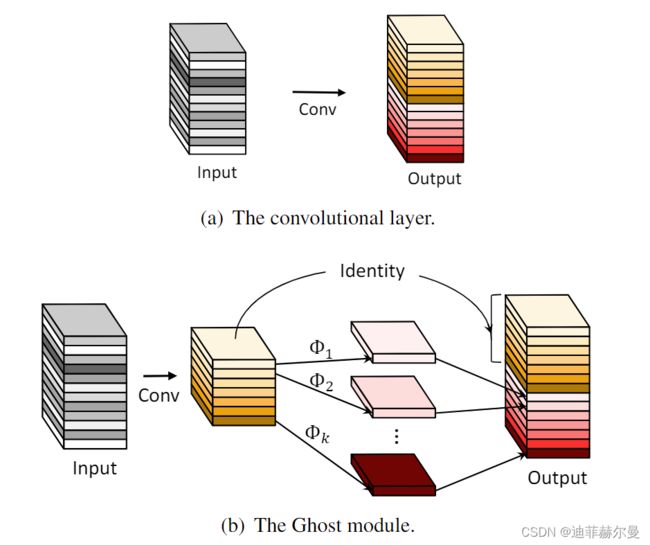
class GhostModule(nn.Module):
    def __init__(self, inp, oup, kernel_size=1, ratio=2, dw_size=3, stride=1, relu=True):
        super(GhostModule, self).__init__()
        #ratio一般会指定成2，保证输出特征层的通道数等于exp
        self.oup = oup
        init_channels = math.ceil(oup / ratio)
        new_channels = init_channels*(ratio-1)

        #利用1x1卷积对输入进来的特征图进行通道的浓缩，获得特征通缩
        #跨通道的特征提取
        self.primary_conv = nn.Sequential(
            nn.Conv2d(inp, init_channels, kernel_size, stride, kernel_size//2, bias=False),  #1x1卷积的输入通道数为GhostModule的输出通道数oup/2
            nn.BatchNorm2d(init_channels),                       #1x1卷积后进行标准化
            nn.ReLU(inplace=True) if relu else nn.Sequential(),  #ReLU激活函数
        )

        #在获得特征浓缩后，使用逐层卷积，获得额外的特征图
        #跨特征点的特征提取    一般会设定大于1的卷积核大小
        self.cheap_operation = nn.Sequential(
            nn.Conv2d(init_channels, new_channels, dw_size, 1, dw_size//2, groups=init_channels, bias=False),  #groups参数的功能就是将普通卷积转换成逐层卷据
            nn.BatchNorm2d(new_channels),
            nn.ReLU(inplace=True) if relu else nn.Sequential(),
        )

    def forward(self, x):
        x1 = self.primary_conv(x)
        x2 = self.cheap_operation(x1)
        #将1x1卷积后的结果和逐层卷积后的结果进行堆叠
        out = torch.cat([x1,x2], dim=1)
        return out[:,:self.oup,:,:]

---

参考文献;
卷积神经网络中的Separable Convolution
空洞卷积（Atrous convolution）
可变形卷积网络