2022高教社杯 国赛数学建模 C题思路
一、C题分析与思路
(赛题出来以后第一时间分享)
三、往届C题常用三大模型
3.1 预测模型
预测模型:
- 神经网络预测、
- 灰色预测、
- 拟合插值预测(线性回归)、
- 时间序列预测、
- 马尔科夫链预测、
- 微分方程预测、
- Logistic 模型等等。
应用领域:人口预测、水资源污染增长预测、病毒蔓延预测、竞赛获胜概率预测、月收入预测、销量预测、经济发展情况预测等在工业、农业、商业等经济领域,以及环境、社会和军事等领域中都有广泛的应用。
预测模型:难度中等。
拟合插值预测:基础简单、容易理解。
拟合算法:matlab拟合工具箱、准确…
插值算法:短期预测、完善补全数据、插值函数、拉格朗日插值法、三次样条插值法…
神经网络预测:现代优化算法、考验编程能力。
人口预测:灰色预测、Logistic 模型…
3.2 优化模型
优化模型:
- 规划模型(目标规划、线性规划、非线性规划、整数规划、动态规划)、
- 图论模型、
- 排队论模型、
- 神经网络模型、
- 现代优化算法(遗传算法、模拟退火算法、蚁群算法、禁忌搜索算法)等等。
应用领域:快递员派送快递的最短路径问题、水资源调度优化问题、高速路口收费站问题、军事行动避空侦察的时机和路线选择、物流选址问题、商区布局规划等各个领域。
优化模型:偏难。
切割木料、地板,使损耗最低、利润最高。
自然水管道铺设问题:图论模型(迪杰斯特拉算法 Dijkstra、克鲁斯卡尔算法 Kruskal)
3.3 评价模型
评价模型:
- 模糊综合评价法、
- 层次分析法、
- 聚类分析法、
- 主成分分析评价法、
- 灰色综合评价法、
- 人工神经网络评价法等等。
应用领域:某区域水资源评价、水利工程项目风险评价、城市发展程度评价、足球教练评价、篮球队评价、水生态评价、大坝安全评价、边坡稳定性评价。
预测模型:偏简单。
常用技术 - 退火算法
放一个年年都用到的技术,退火算法
按我个人的理解的话,是解决组合优化的问题是,使用随机化的方法得到新解,如果新解比旧解要好,那么就接受。如果新解没有旧解好,那么也按一定概率[exp(-delta_f/T)]接受。T是一个温度,内循环就产生新解直到达到平稳,外循环就退火(缓慢的速率温度)。到结束温度时,会收敛到最优解。那么我用的示例是旅行商问题。直接贴代码吧。
from matplotlib import pyplot as plt
import numpy as np
def coordinate_init(size):
#产生坐标字典
coordinate_dict = {}
coordinate_dict[0] = (0, 0)#起点是(0,0)
for i in range(1, size + 1):#顺序标号随机坐标
coordinate_dict[i] = (np.random.uniform(0, size), np.random.uniform(0, size))
coordinate_dict[size + 1] = (0, 0)#终点是(0,0)
return coordinate_dict
def distance_matrix(coordinate_dict,size):#生成距离矩阵
d=np.zeros((size+2,size+2))
for i in range(size+1):
for j in range(size+1):
if(i==j):
continue
if(d[i][j]!=0):
continue
x1 = coordinate_dict[i][0]
y1 = coordinate_dict[i][1]
x2 = coordinate_dict[j][0]
y2 = coordinate_dict[j][1]
distance=np.sqrt((x1-x2)**2+(y1-y2)**2)
if(i==0):
d[i][j]=d[size+1][j]=d[j][i]=d[j][size+1]=distance
else:
d[i][j]=d[j][i]=distance
return d
def path_length(d_matrix,path_list,size):#计算路径长度
length=0
for i in range(size+1):
length+=d_matrix[path_list[i]][path_list[i+1]]
return length
def new_path(path_list,size):
#二交换法
change_head = np.random.randint(1,size+1)
change_tail = np.random.randint(1,size+1)
if(change_head>change_tail):
change_head,change_tail=change_tail,change_head
change_list = path_list[change_head:change_tail + 1]
change_list.reverse()#change_head与change_tail之间的路径反序
new_path_list = path_list[:change_head] + change_list + path_list[change_tail + 1:]
return change_head,change_tail,new_path_list
def diff_old_new(d_matrix,path_list,new_path_list,head,tail):#计算新旧路径的长度之差
old_length=d_matrix[path_list[head-1]][path_list[head]]+d_matrix[path_list[tail]][path_list[tail+1]]
new_length=d_matrix[new_path_list[head-1]][new_path_list[head]]+d_matrix[new_path_list[tail]][new_path_list[tail+1]]
delta_p=new_length-old_length
return delta_p
T_start=2000#起始温度
T_end=1e-20#结束温度
a=0.995#降温速率
Lk=50#内循环次数,马尔科夫链长
size=20
coordinate_dict=coordinate_init(size)
print(coordinate_dict)#打印坐标字典
path_list=list(range(size+2))#初始化路径
d=distance_matrix(coordinate_dict,size)#距离矩阵的生成
best_path=path_length(d,path_list,size)#初始化最好路径长度
print('初始路径:',path_list)
print('初始路径长度:',best_path)
best_path_temp=[]#记录每个温度下最好路径长度
best_path_list=[]#用于记录历史上最好路径
balanced_path_list=path_list#记录每个温度下的平衡路径
balenced_path_temp=[]#记录每个温度下平衡路径(局部最优)的长度
while T_start>T_end:
for i in range(Lk):
head, tail, new_path_list = new_path(path_list, size)
delta_p = diff_old_new(d, path_list, new_path_list, head, tail)
if delta_p < 0:#接受状态
balanced_path_list=path_list = new_path_list
new_len=path_length(d,path_list,size)
if(new_len
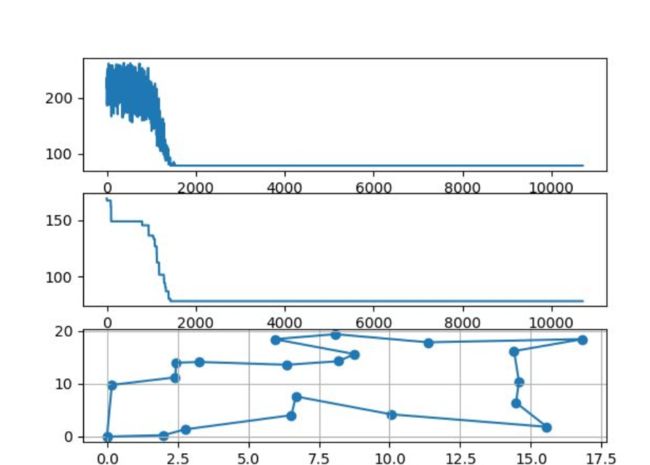
说实话,我最讨厌别人的博客只有代码没有输出,所以,输出还是要有的:
{0: (0, 0), 1: (8.0813445997638, 19.378598885734345), 2: (5.9336947559652735, 18.43334356701462), 3: (2.4187354288286844, 11.208318685158517), 4: (11.364680404115896, 17.838011084801682), 5: (14.57899298590396, 10.443803487389676), 6: (14.475687688871977, 6.430692753878264), 7: (15.564547884718248, 1.8489819656041484), 8: (2.762034307781256, 1.3609270597085188), 9: (2.4449326896325507, 13.971590679990305), 10: (6.376590999061471, 13.590205047457003), 11: (2.0008565516450005, 0.25779568392405805), 12: (8.756514935267091, 15.616855386568506), 13: (8.19333746755698, 14.267482040877905), 14: (6.688671060971291, 7.594062408648769), 15: (16.826772155106706, 18.439257279177564), 16: (0.17109735207725185, 9.772548332790812), 17: (10.057710887083482, 4.213811533920735), 18: (14.404568409630825, 16.182396066315434), 19: (6.522071276732497, 4.044136354883117), 20: (3.2651888440785837, 14.12486494048631), 21: (0, 0)}
初始路径: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21]
初始路径长度: 225.0507842833548
结束温度的局部最优路径: [0, 11, 8, 19, 14, 17, 7, 6, 5, 18, 15, 4, 1, 2, 12, 13, 10, 20, 9, 3, 16, 21]
结束温度的局部最优路径长度: 78.12501363830815
最好路径: [0, 11, 8, 19, 14, 17, 7, 6, 5, 18, 15, 4, 1, 2, 12, 13, 10, 20, 9, 3, 16, 21]
最好路径长度: 78.12501363830815