(二) 三维点云课程---Spectral Clustering(谱聚类)
三维点云课程—Spectral Clustering
三维点云课程---Spectral Clustering
- 三维点云课程---Spectral Clustering
-
- 1.前言
-
- 1.1 c u t ( A i , A i ‾ ) cut(A_i,\overline {A_i}) cut(Ai,Ai)的解释
- 1.2 ∣ A i ∣ , v o l ( A i ) |A_i|,vol(A_i) ∣Ai∣,vol(Ai)的解释
- 2.原理推导
-
- 2.1知识铺垫
-
- 2.1.1相似矩阵W三个建立方法
- 2.1.2 对角矩阵D
- 2.1.2 拉普拉斯矩阵L
- 2.2直观理解
- 2.3 数学推导
-
- 2.3.1 k=2的情况
- 2.3.2 k ≥ 2 \ge2 ≥2的情况
- 3.谱聚类的步骤及效果
-
- 3.1步骤
-
- 3.1.1非归一化步骤
- 3.1.1归一化步骤
- 3.2效果
- 3.3 谱聚类自动判断聚类数
- 4.谱聚类的优、缺点
-
- 4.1 优点
- 4.2 缺点
由于GMM需要人工设置聚类数且工作在欧式距离上,对形状有一定的假设(数据点分布近似为椭圆形状)等缺点,Spectral Clustering 谱聚类可以克服这些缺点,对谱聚类的原理进行解析
1.前言
谱聚类分为非归一化和归一化的,分别近似于图论中的RatioCut和NormalizedCut,表达形式如下
R a t i o C u t ( A 1 , . . . , A k ) = ∑ i = 1 k c u t ( A i , A i ‾ ) ∣ A i ∣ N c u t ( A 1 , . . . , A k ) = ∑ i = 1 k c u t ( A i , A i ‾ ) v o l ( A i ) RatioCut(A_1,...,A_k)=\sum \limits_{i=1}^k \frac {cut(A_i,\overline {A_i})}{|A_i|} \\ Ncut(A_1,...,A_k)=\sum \limits_{i=1}^k \frac{cut(A_i,\overline {A_i})}{vol(A_i)} RatioCut(A1,...,Ak)=i=1∑k∣Ai∣cut(Ai,Ai)Ncut(A1,...,Ak)=i=1∑kvol(Ai)cut(Ai,Ai)
其中 A i ‾ \overline {A_i} Ai是 A i A_i Ai的补集,对于 c u t ( A i , A i ‾ ) , ∣ A i ∣ , v o l ( A i ) cut(A_i,\overline {A_i}),|A_i|,vol(A_i) cut(Ai,Ai),∣Ai∣,vol(Ai)解释如下
1.1 c u t ( A i , A i ‾ ) cut(A_i,\overline {A_i}) cut(Ai,Ai)的解释
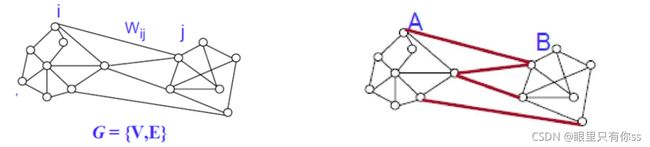
对于两个子集A,B,子图 G = ( V , E ) G=(V,E) G=(V,E),使得连接A,B的边的权重( w i j w_{ij} wij)最小,权重可以自己定义,可以通过连接性,距离等
c u t ( A , B ) = ∑ i ∈ A , j ∈ B w i j cut(A,B)=\sum \limits_{i\in A,j \in B}w_{ij} cut(A,B)=i∈A,j∈B∑wij
对于k个子集,定义如下
c u t ( A 1 , . . . , A k ) = ∑ i = 1 k c u t ( A i , A i ‾ ) cut(A_1,...,A_k)=\sum \limits_{i=1}^k cut(A_i,\overline {A_i}) cut(A1,...,Ak)=i=1∑kcut(Ai,Ai)
1.2 ∣ A i ∣ , v o l ( A i ) |A_i|,vol(A_i) ∣Ai∣,vol(Ai)的解释
如果仅仅使用上面的公式,可能会出现以下的问题:理论上是想在红色黑色的中间的位置切一刀,但根据上面的公式,可能会在蓝色的点的附件切一刀,因为该位置权重最小。
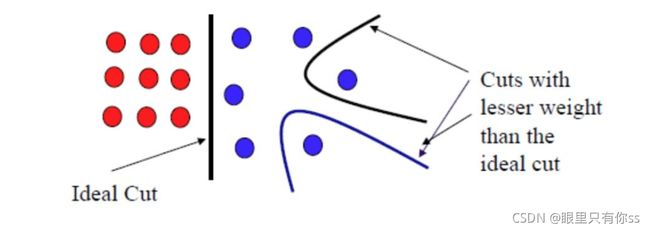
因此需要增加一些限制,使得切割的 A i A_i Ai不要太小,那么怎么定义 A i A_i Ai的大小呢?对于非归一化和归一化,追求的目标不同, A i A_i Ai的大小自然不同。
S i z e ( A ) : U n N o r m a l i z e d ∼ R a t i o C u t → ∣ A ∣ : A 中 顶 点 的 数 量 S i z e ( A ) : N o r m a l i z e d ∼ N C u t → v o l ( A ) = ∑ i ∈ A d i , d i = ∑ j = 1 n w i j : 点 i 的 权 重 之 和 Size(A):UnNormalized \sim RatioCut \to |A|:A中顶点的数量 \\ Size(A):Normalized \sim NCut \to vol(A)=\sum \limits_{i \in A}d_i,d_i=\sum \limits_{j=1}^n w_{ij}:点i的权重之和 Size(A):UnNormalized∼RatioCut→∣A∣:A中顶点的数量Size(A):Normalized∼NCut→vol(A)=i∈A∑di,di=j=1∑nwij:点i的权重之和
在非归一化的谱聚类中,GraphCut追求的目标是不同类之间的点不同,更倾向于一个类中的数据点是均等的;归一化的谱聚类中,GraphCut追求的目标是同一个类之间相似,更倾向于每一个类中的粒度是相等的。在实际工程项目中,多采用归一化的谱聚类,但在这里为了方便推导,采用非归一化的谱聚类进行推导。
下图中黑色的竖线表示非归一化的结果,红色的竖线表示归一化的结果
2.原理推导
2.1知识铺垫
其实谱聚类需要三个矩阵,相似矩阵W,对角矩阵D,拉普拉斯矩阵L。现在对这三个矩阵进行解释。
2.1.1相似矩阵W三个建立方法
1.Radius 领域搜索建立。 w i j = d ( v i , v j ) w_{ij}=d(v_i,v_j) wij=d(vi,vj)
2.KNN搜索。 w i j = d ( v i , v j ) w_{ij}=d(v_i,v_j) wij=d(vi,vj)
a)建立一个边,如果 v i v_i vi是 v j v_j vjKNN领域的一个邻居,或者 v j v_j vj是 v i v_i viKNN领域的一个邻居
b)建立一个边,如果 v i v_i vi是 v j v_j vjKNN领域的一个邻居,并且 v j v_j vj是 v i v_i viKNN领域的一个邻居
3.全连接图
2.1.2 对角矩阵D
矩阵D是一个对角矩阵, d i = ∑ j = 1 n w i j d_i=\sum \limits_{j=1}^n w_{ij} di=j=1∑nwij,表示,对角线的每一个元素都是相似矩阵W的每一行之和
2.1.2 拉普拉斯矩阵L
非归一化拉普拉斯矩阵 L = D − W L=D-W L=D−W,归一化拉普拉斯矩阵
L s y m = D − 1 / 2 L D 1 / 2 = I − D − 1 / 2 W D − 1 / 2 L r w = D − 1 L = I − D − 1 W L_{sym}=D^{-1/2}LD^{1/2}=I-D^{-1/2}WD^{-1/2} \\ L_{rw}=D^{-1}L=I-D^{-1}W Lsym=D−1/2LD1/2=I−D−1/2WD−1/2Lrw=D−1L=I−D−1W
介绍几个关于拉普拉斯矩阵L的性质
1.对于任意的向量 f ∈ R n f \in R^n f∈Rn,都有
f T L f = 1 2 ∑ i = 1 n ∑ j = 1 n w i j ( f i − f j ) 2 f^TLf=\frac{1}{2}\sum \limits_{i=1}^n \sum \limits_{j=1}^n w_{ij}(f_i-f_j)^2 fTLf=21i=1∑nj=1∑nwij(fi−fj)2
证明:
f T L f = f T D f − f T W f = ∑ i = 1 n f i 2 d i − ∑ i = 1 n ∑ j = 1 n f i f j w i j = 1 2 ( ∑ i = 1 n f i 2 d i − 2 ∑ i = 1 n ∑ j = 1 n f i f j w i j + ∑ j = 1 n f j 2 d j ) = 1 2 ( ∑ i = 1 n ∑ j = 1 n w i j f i 2 − 2 ∑ i = 1 n ∑ j = 1 n f i f j w i j + ∑ j = 1 n ∑ i = 1 n w j i f j 2 ) = 1 2 ∑ i = 1 n ∑ j = 1 n w i j ( f i − f j ) 2 \begin{array}{l} {f^T}Lf = {f^T}Df - {f^T}Wf\\ \quad \quad \quad {\rm{ = }}\sum\limits_{i = 1}^n {{f_i}^2{d_i}} - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{f_i}{f_j}{w_{ij}}} } \\ \quad \quad \quad{\rm{ = }}\frac{1}{2}(\sum\limits_{i = 1}^n {{f_i}^2{d_i}} - 2\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{f_i}{f_j}{w_{ij}}} } + \sum\limits_{j = 1}^n {{f_j}^2{d_j}} )\\ \quad \quad \quad{\rm{ = }}\frac{1}{2}(\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{w_{ij}}f_i^2} } - 2\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{f_i}{f_j}{w_{ij}}} } + \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {{w_{ji}}f_j^2} } )\\ \quad \quad \quad {\rm{ = }}\frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{w_{ij}}{{({f_i} - {f_j})}^2}} } \end{array} fTLf=fTDf−fTWf=i=1∑nfi2di−i=1∑nj=1∑nfifjwij=21(i=1∑nfi2di−2i=1∑nj=1∑nfifjwij+j=1∑nfj2dj)=21(i=1∑nj=1∑nwijfi2−2i=1∑nj=1∑nfifjwij+j=1∑ni=1∑nwjifj2)=21i=1∑nj=1∑nwij(fi−fj)2
其中 d i = ∑ j = 1 n w i j d_i=\sum \limits_{j=1}^n w_{ij} di=j=1∑nwij
2. L L L是对称半正定的矩阵
证明:
对称性: L T = ( D − W ) T = ( D T − W T ) = ( D − W ) = L L^T=(D-W)^T=(D^T-W^T)=(D-W)=L LT=(D−W)T=(DT−WT)=(D−W)=L
半正定: f T L f = 1 2 ∑ i = 1 n ∑ j = 1 n w i j ( f i − f j ) 2 ≥ = 0 f^TLf=\frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{w_{ij}}{{({f_i} - {f_j})}^2}} } \ge=0 fTLf=21i=1∑nj=1∑nwij(fi−fj)2≥=0
3.L的最小特征值为0,其对应的特征向量为常数向量,方便起见,这里用 1 1 1表示。
证明:
L f = ( D − W ) f = D f − W f = [ d 1 f 1 . . . d i − f i . . . d n − f n ] − [ w 11 f 1 + . . . w 1 n f n . . . w i 1 f 1 + . . . w i n f n . . . w n 1 f 1 + . . . w n n f n ] = [ d 1 f 1 . . . d i − f i . . . d n − f n ] − [ ∑ j = 1 n w 1 j f j . . . ∑ j = 1 n w i j f j . . . ∑ j = 1 n w n j f j ] = [ . . . , d i f i − ∑ j = 1 n w i j f j , . . . ] T = 0 ∙ f Lf=(D-W)f=Df-Wf\\ =\begin{bmatrix} {{d_1}{f_1}}\\ {...}\\ {{d_i} - {f_i}}\\ {...}\\ {{d_n} - {f_n}} \end{bmatrix} - \begin{bmatrix} {{w_{11}}{f_1} + ...{w_{1n}}{f_n}}\\ {...}\\ {{w_{i1}}{f_1} + ...{w_{in}}{f_n}}\\ {...}\\ {{w_{n1}}{f_1} + ...{w_{nn}}{f_n}} \end{bmatrix} =\begin{bmatrix} {{d_1}{f_1}}\\ {...}\\ {{d_i} - {f_i}}\\ {...}\\ {{d_n} - {f_n}} \end{bmatrix} -\begin{bmatrix} {\sum\limits_{j = 1}^n {{w_{1j}}{f_j}} }\\ {...}\\ {\sum\limits_{j = 1}^n {{w_{ij}}{f_j}} }\\ {...}\\ {\sum\limits_{j = 1}^n {{w_{nj}}{f_j}} } \end{bmatrix}\\ ={\begin{bmatrix} {...,}&{{d_i}{f_i} - \sum\limits_{j = 1}^n {{w_{ij}}{f_j}} ,}&{...} \end{bmatrix}^T} = 0 \bullet f Lf=(D−W)f=Df−Wf=⎣⎢⎢⎢⎢⎡d1f1...di−fi...dn−fn⎦⎥⎥⎥⎥⎤−⎣⎢⎢⎢⎢⎡w11f1+...w1nfn...wi1f1+...winfn...wn1f1+...wnnfn⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡d1f1...di−fi...dn−fn⎦⎥⎥⎥⎥⎤−⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡j=1∑nw1jfj...j=1∑nwijfj...j=1∑nwnjfj⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤=[...,difi−j=1∑nwijfj,...]T=0∙f
上式成立的条件是当且仅当f为常量向量,此时L的特征值为0
4.L的特征值是非负的,即 0 = λ 1 ≤ λ 2 ≤ . . . ≤ λ n 0=\lambda_1 \le \lambda_2 \le... \le \lambda_n 0=λ1≤λ2≤...≤λn
证明:通过2,3显然成立
2.2直观理解
情况一:节点0与节点5不相连
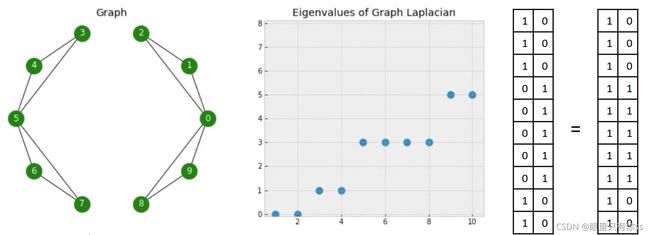
左边是10个顶点的连接情况,中间是拉普拉斯矩阵L的特征值分布情况,存在两个0的特征值,右边是两个特征值0对应的特征向量。
情况二:节点0与节点5相连
当节点0与节点5相连时,相似矩阵W,拉普拉斯特征值和特征向量变化情况如下

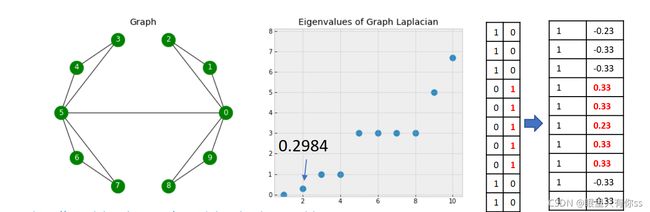
由于连接了节点0和节点5,原来的零特征值由2个变为1个,但同时也存在一个接近0的特征值0.2984,因为加入的权重是1,试想一下,如果加入的权重比较小,那么特征值就会趋近于0,此时对应的权重就比较小,那么“这条线就是切割分类的线”。
通过以上两种可以得知,有多少个连通域,就有多少个0特征值。一个连通图的特征值至少有一个为0,即至少存在一个独立分区,就是自己本身。如果有两个特征值为0,则存在两个独立分区。并且可以通过0对应的特征向量得知这个类有多少个点属于一类,其中有一个特征向量为常量向量,这里为1,其实为2,3都可以。
2.3 数学推导
2.3.1 k=2的情况
对于两个不相交的子集 A , B ∈ V A,B\in V A,B∈V,那么
c u t ( A , B ) = ∑ i ∈ A , j ∈ B w i j cut(A,B)=\sum \limits_{i \in A,j\in B}{w_{ij}} cut(A,B)=i∈A,j∈B∑wij
那么对于非归一化和归一化
R a t i o C u t ( A 1 , . . . , A k ) = ∑ i = 1 k c u t ( A i , A i ‾ ) ∣ A i ∣ N c u t ( A 1 , . . . , A k ) = ∑ i = 1 k c u t ( A i , A i ‾ ) v o l ( A i ) RatioCut(A_1,...,A_k)=\sum \limits_{i=1}^k \frac {cut(A_i,\overline {A_i})}{|A_i|} \\ Ncut(A_1,...,A_k)=\sum \limits_{i=1}^k \frac{cut(A_i,\overline {A_i})}{vol(A_i)} RatioCut(A1,...,Ak)=i=1∑k∣Ai∣cut(Ai,Ai)Ncut(A1,...,Ak)=i=1∑kvol(Ai)cut(Ai,Ai)
方便起见,所有推导基于非归一化。谱聚类的问题就是最小化RatioCut函数,即
min A ⊂ V R a t i o C u t ( A , A ‾ ) = min A ⊂ V ( c u t ( A , A ‾ ) ∣ A ∣ + c u t ( A ‾ , A ) ∣ A ‾ ∣ ) \mathop {\min }\limits_{A \subset V} RatioCut(A,\overline A ) = \mathop {\min }\limits_{A \subset V} (\frac{{cut(A,\overline A )}}{{|A|}} + \frac{{cut(\overline A ,A)}}{{|\overline A |}}) A⊂VminRatioCut(A,A)=A⊂Vmin(∣A∣cut(A,A)+∣A∣cut(A,A))
给予一个子集 A ⊂ V A \subset V A⊂V,构建一个向量 f = [ f 1 , . . . , f n ] T ∈ R n f=[f_1,...,f_n]^T \in R^n f=[f1,...,fn]T∈Rn,构建如下(假设 f f f已经成功构建出来的,实际上 f f f是不知道长什么的)
f i = { ∣ A ‾ ∣ / ∣ A ∣ i f v i ∈ A ∣ A ∣ / ∣ A ‾ ∣ i f v i ∈ A ‾ {f_i} = \left\{ \begin{array}{l} \sqrt {|\overline A |/|A|} \quad \quad \quad {\rm{ if }}\quad{v_i} \in A\\ \sqrt {|A|/|\overline A |} \quad \quad \quad {\rm{ if }}\quad{v_i} \in \overline A \end{array} \right. fi=⎩⎨⎧∣A∣/∣A∣ifvi∈A∣A∣/∣A∣ifvi∈A
其实此时就可以通过 f i f_i fi的正负就可以判断 v i v_i vi是否属于A类了
{ v i ∈ A i f f i ≥ 0 v i ∈ A ‾ i f f i < 0 \left\{ \begin{array}{l} {v_i} \in A\quad\quad{\rm{ if }}\quad{f_i} \ge 0\\ {v_i} \in \overline A \quad\quad{\rm{if }}\quad{f_i} < 0 \end{array} \right. {vi∈Aiffi≥0vi∈Aiffi<0
那么
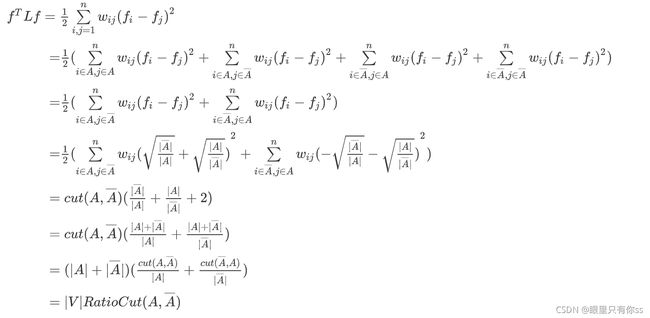
其中 ∣ V ∣ |V| ∣V∣表示原来没有切的图中还有多少个点。
另外, f f f是垂直于常量向量,且 ∣ ∣ f ∣ ∣ = n ||f||=\sqrt{n} ∣∣f∣∣=n
证明如下
f T 1 = ∑ i = 1 n f i = ∑ i ∈ A ∣ A ‾ ∣ ∣ A ∣ − ∑ i ∈ A ‾ ∣ A ∣ ∣ A ‾ ∣ = ∣ A ∣ ∣ A ‾ ∣ ∣ A ∣ − ∣ A ‾ ∣ ∣ A ∣ ∣ A ‾ ∣ = 0 ∣ ∣ f ∣ ∣ 2 = ∑ i = 1 n f i 2 = ∣ A ∣ ∣ A ‾ ∣ ∣ A ∣ + ∣ A ‾ ∣ ∣ A ∣ ∣ A ‾ ∣ = ∣ A ∣ + ∣ A ‾ ∣ = n {f^T}1 = \sum\limits_{i = 1}^n {{f_i}} = \sum\limits_{i \in A} {\sqrt {\frac{{|\overline A |}}{{|A|}}} } - \sum\limits_{i \in \overline A } {\sqrt {\frac{{|A|}}{{|\overline A |}}} } = |A|\sqrt {\frac{{|\overline A |}}{{|A|}}} - |\overline A |\sqrt {\frac{{|A|}}{{|\overline A |}}} = 0\\ ||f|{|^2} = \sum\limits_{i = 1}^n {{f_i}^2} = |A|\frac{{|\overline A |}}{{|A|}} + |\overline A |\frac{{|A|}}{{|\overline A |}} = |A| + |\overline A | = n fT1=i=1∑nfi=i∈A∑∣A∣∣A∣−i∈A∑∣A∣∣A∣=∣A∣∣A∣∣A∣−∣A∣∣A∣∣A∣=0∣∣f∣∣2=i=1∑nfi2=∣A∣∣A∣∣A∣+∣A∣∣A∣∣A∣=∣A∣+∣A∣=n
因此原先最小化图切问题转化为
min A ⊂ V f T L f , s . t . , f ⊥ 1 , ∣ ∣ f ∣ ∣ = n , f i = { ∣ A ‾ ∣ / ∣ A ∣ i f v i ∈ A ∣ A ∣ / ∣ A ‾ ∣ i f v i ∈ A ‾ \mathop {\min }\limits_{A \subset V} f^TLf,s.t.,f \bot 1,||f||=\sqrt{n},{f_i} = \left\{ \begin{array}{l} \sqrt {|\overline A |/|A|} \quad \quad \quad {\rm{ if }}\quad{v_i} \in A\\ \sqrt {|A|/|\overline A |} \quad \quad \quad {\rm{ if }}\quad{v_i} \in \overline A \end{array} \right. A⊂VminfTLf,s.t.,f⊥1,∣∣f∣∣=n,fi=⎩⎨⎧∣A∣/∣A∣ifvi∈A∣A∣/∣A∣ifvi∈A
由于 f i f_i fi是假设的,因此上式近似为
min A ⊂ V f T L f , s . t . , f ⊥ 1 , ∣ ∣ f ∣ ∣ = n \mathop {\min }\limits_{A \subset V} f^TLf,s.t.,f \bot 1,||f||=\sqrt{n} A⊂VminfTLf,s.t.,f⊥1,∣∣f∣∣=n
遇见对称矩阵 A A A,求解类似 x T A x x^TAx xTAx的最大最小值,采用Rayleigh商进行求解。由于Rayleigh商定理本身没有条件,但是对于上式存在 f ⊥ 1 , ∣ ∣ f ∣ ∣ = n f \bot 1,||f||=\sqrt{n} f⊥1,∣∣f∣∣=n限制条件,那该怎么处理呢?对于 L L L的最小特征值就是 m i n f T L f minf^TLf minfTLf的最小值,但是 f f f是有条件的,好在 L L L的最小特征值0对应的特征向量为常数,又因为常数不垂直于1,取 L L L矩阵的第二小特征值作为 f T L f f^TLf fTLf的最小值,对应的特征向量就是 f f f。
现在存在一个问题,就是怎么通过上述得到的 f f f进行分类呢,这时肯定就有人说使用
f i = { ∣ A ‾ ∣ / ∣ A ∣ i f v i ∈ A ∣ A ∣ / ∣ A ‾ ∣ i f v i ∈ A ‾ {f_i} = \left\{ \begin{array}{l} \sqrt {|\overline A |/|A|} \quad \quad \quad {\rm{ if }}\quad{v_i} \in A\\ \sqrt {|A|/|\overline A |} \quad \quad \quad {\rm{ if }}\quad{v_i} \in \overline A \end{array} \right. fi=⎩⎨⎧∣A∣/∣A∣ifvi∈A∣A∣/∣A∣ifvi∈A
通过 f i f_i fi的正负来进行判断,但是上式假设出来的。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Fm5mXbsP-1635251405573)(E:\资料\三维重建课程\第四课时\图片\理想和非理想.png)]
左图是已知 f i f_i fi的分布,右图 f i f_i fi是未知的,且黄色的点是上述得到的特征向量 f 2 f_2 f2的点。那么此时需要将得到的 f 2 f_2 f2和常量向量 f 1 f_1 f1组合起来,采用KMeans方法进行分类。那么为什么需要结合 f 1 f_1 f1,只采用 f 2 f_2 f2不就可以了吗?如果只存在两个孤立的连通域,只用 f 1 f_1 f1就可以了,但是如果因为两个连通域之间有连线,只用 f 1 f_1 f1就不可以了。其实 f 1 f_1 f1表示的是连通域的信息, f 2 f_2 f2是图的构造。
2.3.2 k ≥ 2 \ge2 ≥2的情况
对于k个分类, A 1 , . . . , A k A_1,...,A_k A1,...,Ak,那么
c u t ( A 1 , . . . , A k ) = ∑ i = 1 k c u t ( A i , A ‾ i ) cut(A_1,...,A_k)=\sum \limits_{i=1}^k{cut(A_i,\overline A_i)} cut(A1,...,Ak)=i=1∑kcut(Ai,Ai)
构造一个Indication矩阵 H ∈ R n × k H \in R^{n \times k} H∈Rn×k
h i j = { 1 / ∣ A i ∣ i f i ∈ A j 0 o t h e r w i s e {h_{ij}} = \left\{ \begin{array}{l} 1/\sqrt {|{A_i}|} \quad \quad {\rm{ if }}\quad i \in {A_j}\\ 0\quad \quad \quad \quad otherwise \end{array} \right. hij={1/∣Ai∣ifi∈Aj0otherwise
举个例子
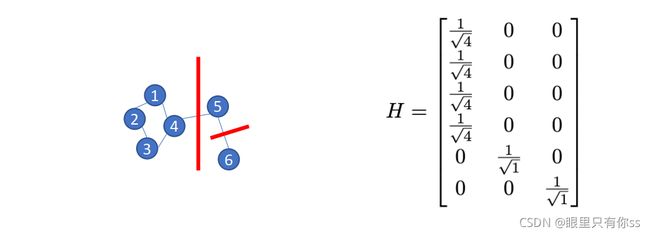
其中 { 1 , 2 , 3 , 4 } ∈ A 1 ; 5 ∈ A 2 ; 6 ∈ A 3 \{1,2,3,4\} \in A_1;5 \in A_2;6\in A_3 {1,2,3,4}∈A1;5∈A2;6∈A3。
类比k=2的情况,我们有
h i T L h i = c u t ( ∣ A i ∣ , ∣ A i ∣ ‾ ) ∣ A i ∣ , h i T L h i = ( H T L H ) i i {h_i}^TL{h_i}=\frac{cut({|A_i|},\overline {|A_i|})}{|A_i|}, {h_i}^TL{h_i} = {({H^T}LH)_{ii}} hiTLhi=∣Ai∣cut(∣Ai∣,∣Ai∣),hiTLhi=(HTLH)ii
那么
R a t i o C u t ( A 1 , . . . , A k ) = ∑ i = 1 k c u t ( ∣ A i ∣ , ∣ A i ∣ ‾ ) ∣ A i ∣ = ∑ i = 1 k h i T L h i = ∑ i = 1 k ( H T L H ) i i = T r ( H T L H ) RatioCut(A_1,...,A_k)=\sum \limits_{i=1}^k \frac{cut({|A_i|},\overline {|A_i|})}{|A_i|}\\ =\sum \limits_{i=1}^kh_i^TLh_i=\sum \limits_{i=1}^k(H^TLH)_{ii}=Tr(H^TLH) RatioCut(A1,...,Ak)=i=1∑k∣Ai∣cut(∣Ai∣,∣Ai∣)=i=1∑khiTLhi=i=1∑k(HTLH)ii=Tr(HTLH)
现在问题转化为
min A 1 , . . . , A k T r ( H T L H ) s . t , H T H = I , h i j = { 1 / ∣ A i ∣ i f i ∈ A j 0 o t h e r w i s e \mathop {\min }\limits_{{A_1},...,{A_k}} Tr(H^TLH) s.t,H^TH=I,{h_{ij}} = \left\{ \begin{array}{l} 1/\sqrt {|{A_i}|} \quad \quad {\rm{ if }}\quad i \in {A_j}\\ 0\quad \quad \quad \quad otherwise \end{array} \right. A1,...,AkminTr(HTLH)s.t,HTH=I,hij={1/∣Ai∣ifi∈Aj0otherwise
近似为
min A 1 , . . . , A k T r ( H T L H ) . s . t , H T H = I \mathop {\min }\limits_{{A_1},...,{A_k}} Tr(H^TLH) .s.t,H^TH=I A1,...,AkminTr(HTLH).s.t,HTH=I
对于矩阵的Rayleigh商,现在给出结论 L L L前k个较小的特征值对应的特征向量组合起来就是 H H H,具体推导过程可以参考之前PCA推导.
3.谱聚类的步骤及效果
3.1步骤
3.1.1非归一化步骤
- 通过图建立一个相似矩阵 W ∈ R n × n W \in R^{n \times n} W∈Rn×n,(相似矩阵建立三选一)
- 计算对角矩阵 D D D,其中 d i j = ∑ j = 1 n w i j d_{ij}=\sum \limits_{j=1}^n{w_{ij}} dij=j=1∑nwij
- 计算非归一化的拉普拉斯矩阵 L = D − W L=D-W L=D−W
- 计算 L L L最小的前k个特征值对应的特征向量 v 1 , . . . , v k v_1,...,v_k v1,...,vk
- 将上述的特征向量按照行的方向进行排列,组合成 V ∈ R n × k V \in R^{n \times k} V∈Rn×k
- 将 V V V的每一行数据,记为 Y = { y i , . . . , y n } Y=\{y_i ,...,y_n\} Y={yi,...,yn}
- 对上述的 Y Y Y进行KMeans操作,得到 C = { C 1 , . . . , C k } C=\{C_1,...,C_k\} C={C1,...,Ck}的聚类结果
- 通过上述 C C C对应的索引,将原始数据进行分类
3.1.1归一化步骤
- 通过图建立一个相似矩阵 W ∈ R n × n W \in R^{n \times n} W∈Rn×n,(相似矩阵建立三选一)
- 计算对角矩阵 D D D,其中 d i j = ∑ j = 1 n w i j d_{ij}=\sum \limits_{j=1}^n{w_{ij}} dij=j=1∑nwij
- 计算归一化的拉普拉斯矩阵 L r w = D − 1 ( D − W ) L_{rw}=D^{-1}(D-W) Lrw=D−1(D−W)
- 计算 L r w L_{rw} Lrw最小的前k个特征值对应的特征向量 v 1 , . . . , v k v_1,...,v_k v1,...,vk
- 将上述的特征向量按照行的方向进行排列,组合成 V ∈ R n × k V \in R^{n \times k} V∈Rn×k
- 将 V V V的每一行数据,记为 Y = { y i , . . . , y n } Y=\{y_i ,...,y_n\} Y={yi,...,yn}
- 对上述的 Y Y Y进行KMeans操作,得到 C = { C 1 , . . . , C k } C=\{C_1,...,C_k\} C={C1,...,Ck}的聚类结果
- 通过上述 C C C对应的索引,将原始数据进行分类
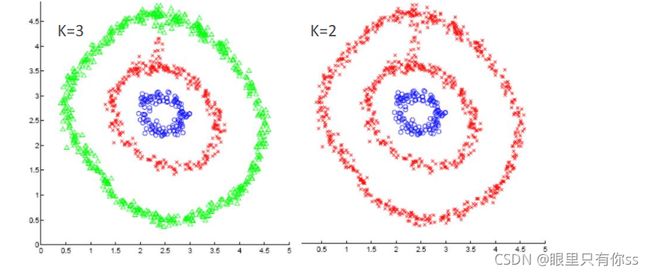
3.2效果
下图即谱聚类的分类的结果,不同GMM和KMeans,谱聚类可以轻易的将圆分开,因为它是工作在图上的,而不是欧式聚类
3.3 谱聚类自动判断聚类数
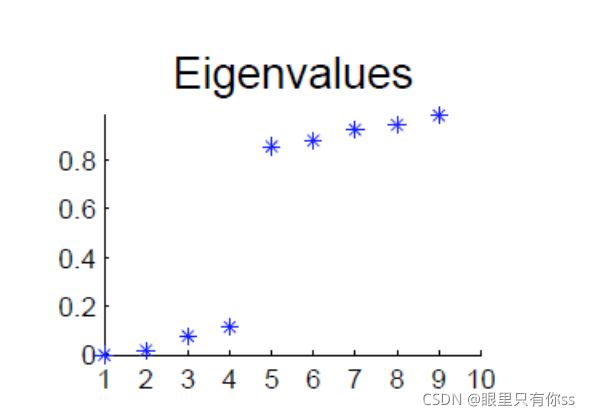
将拉普拉斯矩阵L的特征值进行从小到大排布,并且记 Δ k = ∣ λ k − λ k − 1 ∣ {\Delta _k} = |{\lambda _k} - {\lambda _{k - 1}}| Δk=∣λk−λk−1∣,如果 Δ k \Delta_k Δk突变,表示特征值由小到大突变,对应于下图的渐变的过程,此时只需要关心突变前k个特征值,此时k=聚类的个数。
4.谱聚类的优、缺点
4.1 优点
- 不会对任何性质进行假设
- 自动的发觉右多少类
- 可以工作在高维空间上
- 工作在图上,并不是欧式距离
4.2 缺点
算法的时间复杂度为 O ( n 3 ) O(n^3) O(n3),效率较低。
注意具体代码参考下一篇,嘻嘻嘻嘻