opencv入门:模板匹配,霍夫变换
模板匹配
再当前图像A 内寻找图像B 最相似的部分,A为输入图像,B为模板图像,操作方法是将模板图B再A 图上滑动,历遍所有像素以完成匹配。

模板匹配基础
result = cv2.matchTemplate(image , templ, method, [mark])
- image 原始图像,必须是8位 或 32位 的浮点型图像
- templ 模板图像,尺寸小于等于原图,并且和原图是相同类型。
- method 匹配方法,通过TemplateMatchModes 实现,

其中 I 表示输入图像,T 表示模板,R表示输出结果图像,x,y 表示位置信息。 - mask 为模板图像的掩模,与模板图像有相同的类型和大小,使用默认就好。。
返回值是由每个位置的比较结果组合构成的一个结果集,类型是单通道32位浮点型,如果输入图像的尺寸是 WH 模板尺寸 wh ,返回值的尺寸为 (W-w+1) * (H-h+1)。进行模板匹配时,模板再原始图内历遍,水平方向上:
- 遍历的起始坐标从原图左边第一个像素值开始,序号从1 开始
- 最后一次比较是模板图再原图右侧时,左上像素点的位置就是 W-w+1 ,这也是水平方向上的比较次数
- 垂直方向同理。也就是说,模板图像要在输入图像内比较(W-w+1)*(H-h+1)次。

这里比较 81 次,结果构成 9X9 的二维数组。
另外,参数method 决定使用不同的查找方法,对于不同的查找方法,返回值也具有不同的含义:
- method 的值为 cv2.TM_SQDIFF 和 cv2.TM_SQDIFF_NORMED 时,result 值为 0 表示匹配度最好,值越大,表示匹配度越差。
- method 的值为 cv2.TM_CCORR、cv2.TM_CCORR_NORMED、cv2.TM_CCOEFF 和cv2.TM_CCOEFF_NORMED 时,result 的值越小表示匹配度越差,值越大表示匹配度越好。
不管使用哪种方法,最后要使用 minVal, maxVal, minLoc, maxLoc = cv2.minMaxLoc( src [, mask] ) 来查找最值的位置
- src单通道数组
- 返回的四个值分别是:最小值,最大值,最小值的位置,最大值的位置,如果其中没有就返回NULL。
- mask 掩模,可以选取的顶子集的极值。
# 举个栗子,method 的值为cv2.TM_SQDIFF,0表示最佳匹配,就要找最小值的位置。
minVal, maxVal, minLoc, maxLoc = cv2.minMaxLoc(matchTemplate 函数的返回值)
topLeft = minLoc # 查找最小值所在的位置
# topLeft 就是匹配位置的左上角,然后使用,w,h 来获得右下角坐标。
bottomRight = (topLeft[0] + w, topLeft[1] + h) #w 和 h 是模板图像的宽度和高度
通过上述方式得到了模板匹配的矩形对角坐标的位置,然后使用Img = cv.rectangle( img, pt1, pt2, color[, thickness]) 将该位置标记出来,,就是画个矩形,参数就是图像,两个点,颜色,矩形线条的宽度

左图那个黑点就是最值了吧。。参数 method 的值为 cv2.TM_CCOEFF,查找的是最大值所在的位置。
多模板匹配
有些情况下,要搜索的模板可能再输入图像内出现了多次,就需要找出多个匹配结果,但是 cv2.minMaxLoc() 仅可以找出最值,无法匹配所有的位置信息,这就需要利用阈值进行处理
- 获取匹配位置的集合。
函数 np.where() 可以获取模板匹配位置的集合,
am=np.array([[3,6,8,77,66],[1,2,88,3,98],[11,2,67,5,2]])
b=np.where(am>5)
print(b)
(array([0, 0, 0, 0, 1, 1, 2, 2], dtype=int64), # 两个数组构成索引
array([1, 2, 3, 4, 2, 4, 0, 2], dtype=int64))
loc = np.where( res >= threshold) # 找出函数cv2.matchTemplate()返回值中,那些位置的值大于阈值 threshold
- 循环,zip()打包构成坐标,,,for i in zip(*模板匹配索引集合):
- 调整坐标,上面得到的坐标是 (行号,列好),但是cv2.rectangele() 的参数是(列号,行号),就调个个loc[::-1]
- 标记匹配图像的位置,
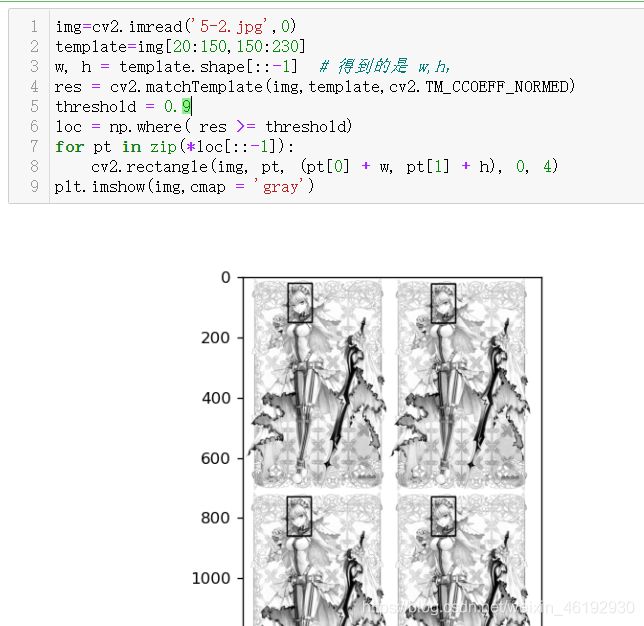
这个阈值应该是根据method 参数的计算公式来设置的,cv2.TM_CCOEFF_NORMED 结果最大值就是1.,,反正一般用这个0.9应该是没问题的吧。。。
霍夫变换
霍夫变换是一种再图像中寻找直线,圆形集其他简单形状的方法,采用类似于投票的方式获取当前图像内的形状集合,
霍夫直线变换
OpenCV 提供了函数 cv2.HoughLines()和函数 cv2.HoughLinesP()用来实现霍夫直线变换。
霍夫变换原理
使用笛卡尔坐标系来说明霍夫变换的基本原理,与普通坐标系对象,构造霍夫坐标系,霍夫坐标系中,横坐标是笛卡尔坐标系中直线的斜率k,纵坐标使用笛卡尔坐标系中直线的截距b。可以说笛卡尔空间内的一条直线确定了霍夫空间的一个点,霍夫空间内的一点确定了笛卡尔空间的一条直线。

对于笛卡尔的一个点,通过该点的直线表示为 y=kx+b ,其中 kb 为任意量,映射到霍夫空间中就是一条直线了。

笛卡尔空间内两个点映射到霍夫空间的情况。

推广到N个点,笛卡尔空间内一条直线上由N个点,霍夫空间中就有穿过 (k,b) 点的N条直线。

综上,霍夫空间内,经过一个点的直线越多,说明其再笛卡尔空间内映射的直线是由越多的点构成的。计算中,我们希望用更多的点构造一条直线,提高直线的可靠性。也就是说一条直线由越多的点构成,它实际存在的可能性越大,可靠性越高。霍夫变换选择直线的基本思路是:选择尽可能多直线交汇的点。
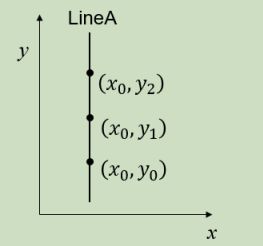
对于垂直的情况,k无穷大,b无法取值,也无法映射到霍夫空间中,那就映射到极坐标系中。。 = cos + sin
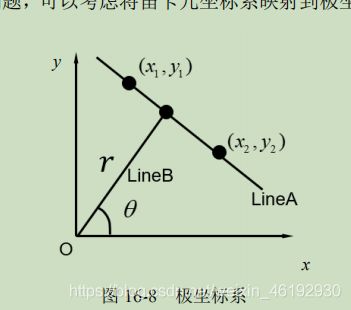
可以这么想,原来 x,y 做直角边 ,r 做斜边sinθ=y/r cosθ=x/r, 第一个两边乘以sinθ,第二个两边乘cosθ,再相加得
极径r 表示与坐标原点的距离,参数 垂线和轴的角度,这种可以表示笛卡尔下所有的直线,并且映射到霍夫空间中的对应关系也一样,极坐标中一点映射到霍夫空间中就是一条线。。。
HoughLines 函数
lines=cv2.HoughLines(image, rho, theta, threshold)
- image 8位单通道二值图,注意修改
- rho以像素为单位的距离r 的精度,一般用1
- theta 为角度的精度。一般情况下,使用的精度是π/180,表示要搜索所有可能的角度
- threshold 阈值,判定直线的数量,大于阈值就认为原图中直线存在,阈值较大就获得较少的直线
- 返回值 中的每个元素都是一对浮点是,表示检测到的直线的参数,即(r,) ,ndarray类型
- 注意这里检测的是直线,不是线段,索引绘制的直线要是穿过整幅图像的。
绘制直线的方法,对于垂直方向上各种角度的直线,计算与图像水平边界(图像第一行和最后一行)的交叉点,然后再这两个交叉点之间画线。水平方向上计算第一列和最后一列。然后使用cv2.line() 画线,即使坐标点不再图像范围内,也可以画出来。
img = cv2.imread('gonglu.jpg')
print(img.shape)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray,50,150,apertureSize = 3) # 边缘检测,两个阈值,算子孔洞
orgb=cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
oShow=orgb.copy()
lines = cv2.HoughLines(edges,1,np.pi/180,200) # (r,)返回值
for line in lines:
rho,theta = line[0]
a = np.cos(theta)
b = np.sin(theta)
x0 = a*rho # x=cos()*r
y0 = b*rho
x1 = int(x0 + 1000*(-b)) # 由参数空间向实际坐标点转换,,就是扩一下坐标1000*(-b) 是个常数。。。
y1 = int(y0 + 1000*(a))
x2 = int(x0 - 1000*(-b))
y2 = int(y0 - 1000*(a))
cv2.line(orgb,(x1,y1),(x2,y2),(0,0,255),2)
plt.subplot(121)
plt.imshow(oShow)
plt.axis('off')
plt.subplot(122)
plt.imshow(orgb)
plt.axis('off')

如果阈值设小了,就满图蓝线了。。那些看起来较粗的,就是几条混在一起了。使用霍夫变换可能将图像中有限个点碰巧对齐的非直线关系检测为直线,而导致误检测,尤其是一些复杂背景的图像,误检测会很明显,于是就有了改进版 概率霍夫变换。
HoughLinesP函数
是霍夫变换算法的优化。它没有考虑所有的点。相反,它只需要一个足以进行线检测的随机点子集即可。另外,它接受直线的最小长度,超过了阈值但是如果直线太短就忽略了。接受直线中允许的最大像素点间距,超过了阈值但是像素点距离很远也忽略。。
lines =cv2.HoughLinesP(image, rho, theta, threshold, minLineLength, maxLineGap)
- minLineLength 直线最小长度,默认0
- maxLineGap 一条线中两点的最大间隔
img = cv2.imread('house.jpg')
print(img.shape)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray,50,150,apertureSize = 3)
orgb=cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
oShow=orgb.copy()
lines = cv2.HoughLinesP(edges,1,np.pi/180,1,minLineLength=60,maxLineGap=10)
for line in lines:
x1,y1,x2,y2 = line[0] # 为啥这就不用那莫名其妙的变换。。
cv2.line(orgb,(x1,y1),(x2,y2),(255,0,0),5)
plt.subplot(121)
plt.imshow(oShow)
plt.axis('off')
plt.subplot(122)
plt.imshow(orgb) # 额 我找的图可能不太好。。。。
plt.axis('off')
霍夫圆环变换
只要是能够用一个参数方程表示的对象,都适合用霍夫变换来检测。
用霍夫圆变换来检测图像中的圆,与使用霍夫直线变换检测的直线的原理类似,不管需要考虑 半径,圆心(x,y)三个参数,方法就是使用两轮筛选,第一轮找到可能存在圆心的位置,第二轮再根据第一轮的结果筛选出半径大小。
circles=cv2.HoughCircles(image, method, dp, minDist, param1, param2, minRadius, maxRadius)
- image 8位单通道灰度图
- method 检测方法,就是HOUGH_GRADIENT 代表霍夫原的两轮检测方法
- dp 累积分辨率,一个分割比率,用来指定图像分辨率与圆心累加器分辨率的比例
- minDist 圆心间的最小间距,存在圆心距离小于该值。的多个原就检测一个,值太小就会有多个临近园被检测,太大,就会漏一些圆。
- param1:该参数是缺省的,在缺省时默认值为 100。它对应的是 Canny 边缘检测器的高阈值(低阈值是高阈值的二分之一)。
- param2:圆心位置必须收到的投票数。只有在第 1 轮筛选过程中,投票数超过该值的圆,才有资格进入第 2 轮的筛选。因此,该值越大,检测到的圆越少;该值越小,检测到的圆越多。这个参数是缺省的,在缺省时具有默认值 100。
- minRadius:圆半径的最小值,小于该值的圆不会被检测出来。该参数是缺省的,在缺省时具有默认值 0,此时该参数不起作用。
- maxRadius:圆半径的最大值,大于该值的圆不会被检测出来。该参数是缺省的,在缺省时具有默认值 0,此时该参数不起作用。
- circles:返回值,由圆心坐标和半径构成的 numpy.ndarray。
img = cv2.imread('qipan.jpg',0)
imgo=cv2.imread('qipan.jpg',-1)
o=cv2.cvtColor(imgo,cv2.COLOR_BGR2RGB)
oshow=o.copy()
img = cv2.medianBlur(img,5) # 进行平滑操作,
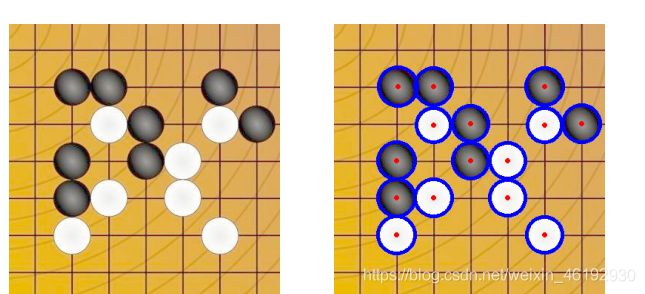
circles = cv2.HoughCircles(img,cv2.HOUGH_GRADIENT,1,10, # 这个参数是非常不好调的,慢慢试试吧。。
param1=50,param2=40,minRadius=20,maxRadius=40)
circles = np.uint16(np.around(circles))
for i in circles[0,:]:
cv2.circle(o,(i[0],i[1]),i[2],(0,0,255),4) # 圆
cv2.circle(o,(i[0],i[1]),2,(255,0,0),2) # 圆心
plt.subplot(121)
plt.imshow(oshow)
plt.axis('off')
plt.subplot(122)
plt.imshow(o)
plt.axis('off')