2022年全国大学生数学建模竞赛E题目-小批量物料生产安排详解+思路+Python代码时序预测模型(二)
目录
前言
一、趋势精化
方法
二、销售单价细化分析
三、算法筛选
1.指标权重计算
2.编秩
3.计算秩和比RSR值
编辑
4.分档.
建模的部分后续将会写出,想要了解更多的欢迎加博主微信,免费获取代码和更多细化思路+模型!
点关注,防走丢,如有纰漏之处,请留言指教,非常感谢
前言
依旧是紧接着上篇文章内容哈,这次我们将更加精细化的将第一问的时间序列模型给全部做出来:
2022年全国大学生数学建模竞赛E题目-小批量物料生产安排详解+思路+Python代码时序预测模型(一)_fanstuck的博客-CSDN博客
这篇文章主要是弥补了上篇文章遗留下来的数据趋势和销售单价的问题,并且将时序预测模型给完全做出来,可以说是任务量满满啊,那么现在我们就开始着手一步一步建模。
一、趋势精化
首先我们根据实际数据来思考,能够反应物料需求波动趋势的可以不用做的那么复杂,毕竟物料种类有283个,如果每个物料都去做一遍趋势分析的话,难免浪费太多时间,而且很多物料需求的发生频次只有一次或者两次,这极大的影响了判断。所以我们这里使用综合统计指标来评测。
方法
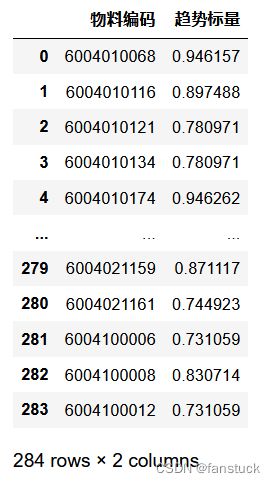
这里既然是趋势,那么我们完全可以使用sigmoid函数来实现一次归一化操作,将数据归一化后直接算出均值即可作为趋势指标。
早在一开始我就像将他们化为无量纲数据来分析趋势了,归一化数据之后融合了数据离散性,再根据均值比较仅得到他们的趋势即可,这样的话避免了需求量的数值影响从而得到更加精准的趋势标量。我们只需要选择标量趋于更大即可,这说明了我们需求量在逐渐增大,更加符合重要物料的性质。
这样一来我们就解决了趋势问题,那么下一个就是销售单价了。
二、销售单价细化分析
这里可能有很多同学朋友想到销售单价那不肯定就是取个最低或者最高就好了嘛,你想想难道单价不是根据需求量来变化的?你单纯拿一个销售单价来分析,而不看需求量,就比如一个物料卖10,一个卖20就选取卖10块的,但是10块的物料只要20个,而卖20的需要30个呢?
我们来看看这个数据:
这一下就差了快2000了,但是如果你取他们的平均价格会损失相当多的信息。
而且根据数据观测我们也发现销售单价也是根据时间在波动所以我们完全可以根据上一个需求量的策略来进行分析,先将销售单价和需求量融合成成本指标:
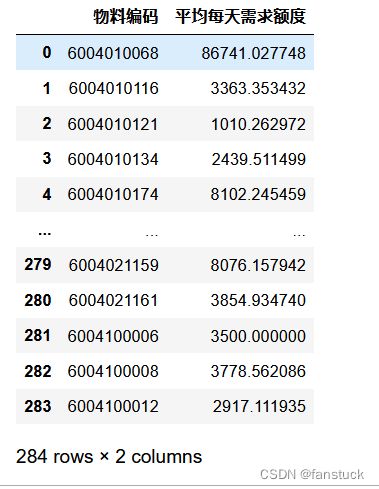
之后再根据聚合后的数据求一次平均从而得到平均每天需求额度,那么这个指标就融合和销售单价,当该指标越大时,说明该物料越值得关注:
这样以来我们就凑齐了所有的参考要素,再组合一遍,得到最终建模数据集:
现在我们就可以根据最终数据来确定最后六种应当重点关注的物料了。
三、算法筛选
决策算法我已经写过很多模型的文章了,包括:
层次分析法(AHP)原理以及应用_fanstuck的博客-CSDN博客_层次分析法原理
一文速学-熵权法实战确定评价指标权重_fanstuck的博客-CSDN博客_熵权法确定权重
秩和比综合评价法(RSR)详解及Python实现和应用_fanstuck的博客-CSDN博客_rsr方法
这里我选择综合性更强的RSR秩和比综合评价法:
一般过程是将效益型指标从小到大排序进行排名、成本型指标从大到小排序进行排名,再计算秩和比,最后统计回归、分档排序。通过秩转换,获得无量纲统计量RSR;在此基础上,运用参数统计分析的概念与方法,研究RSR的分布;以RSR值对评价对象的优劣直接排序或分档排序,从而对评价对象做出综合评价。
1.指标权重计算
进行结果评定时我们知道影响因素的权重大小都是不一致的,我们需要先计算出各个指标的权重再进行加权秩和比,不然各个指标之间的信息差就没有意义。
计算指标权重的方法有AHP、熵权法或是自定义权重,笔者均写过AHP和熵权法.
这里我们用熵权法得到权重:
从而得到相应的权重,之后进行
2.编秩
采用整秩法:
一个![]() 行
行![]() 列的矩阵中,其对应的RSR计算公式为:
列的矩阵中,其对应的RSR计算公式为:
![]()
其中![]() ;
;![]() ,
,![]() 表示为第
表示为第![]() 行第
行第![]() 列元素的秩。
列元素的秩。
当个评价指标的权重不同时,计算加权秩和比为
![]()
![]() 表示第第
表示第第![]() 个指标的权重。RSR值无量纲,最小值为
个指标的权重。RSR值无量纲,最小值为![]() ,最大值为1.
,最大值为1.
3.计算秩和比RSR值
4.分档.
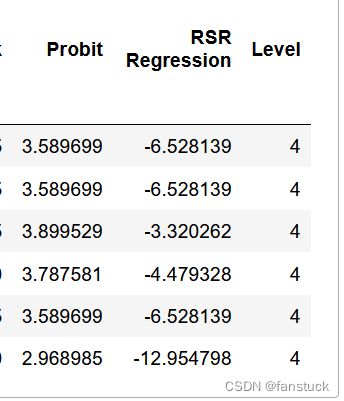
按照回归方程推算所对应的RSR估计值对评价对象进行分档排序,分档数由研究者根据实际情况决定。
● 通过RSR拟合值,以及上一表格中的RSR临界(拟合值)进行区间比较,进而得到分档等级水平;
● 分档等级Level数字越大表示等级水平越高,即效应越好。
得到最终六个最重要的物料编码。
建模的部分后续将会写出,想要了解更多的欢迎加博主微信,免费获取代码和更多细化思路+模型!
点关注,防走丢,如有纰漏之处,请留言指教,非常感谢
以上就是本期全部内容。我是fanstuck ,有问题大家随时留言讨论 ,我们下期见。