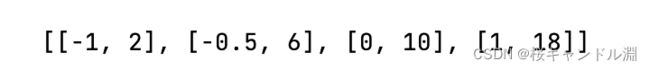【机器学习笔记】【数据预处理】

目录

一、数据无量纲化

1.preprocessing.MinMaxScaler归一化

①归一化到[0,1]以外的范围

②用numpy实现归一化

③逆转归一化

2.preprocessing.StandardScaler标准化

3.总结

StandardScaler和MinMaxScaler选哪个？

二、处理缺失值

1.impute.SimpleImputer

①分别用平均值，中位数，0值填充空值 

②使用众数填补缺失值

③用numpy或者pandas填补缺失值

三、编码与哑变量

1.preprocessing.LabelEncoder标签编码

①逆转编码

2.preprocessing.OrdinalEncoder特征编码

3.preprocessing.OneHotEncoder独热编码

①还原原矩阵

②获取稀疏矩阵对应的列名

③合并数据

四、二值化与分段

1.sklearn.preprocessing.Binarizer二值化

①二值化特征 

②二值化标签

2.preprocessing.KBinsDiscretizer分箱

---

一、数据无量纲化

#建模之前的流程
#1.获取数据
#2.数据预处理
#3.特征工程（挑选相关特征，或者生成新的特征（降维或者计算））
# （降低计算成本，提升模型上限）
#4.建模
#5.上线

模块preprocessing：几乎包含数据预处理的所有内容
模块Impute：填补缺失值专用
模块feature_selection：包含特征选择的各种方法的实践

数据无量纲化
        在机器学习算法实践中，我们往往有着将不同规格的数据转换到同一规格，或不同分布的数据转换到某个特定分布的需求，这种需求统称为将数据“无量纲化”。譬如梯度和矩阵为核心的算法中，譬如逻辑回归，支持向量机，神经网络，无量纲化可以加快求解速度；而在距离类模型，譬如K近邻，K-Means聚类中，无量纲化可以帮我们提升模型精度，避免某一个取值范围特别大的特征对距离计算造成影响。

（一个特例是决策树和树的集成算法们，对决策树我们不需要无量纲化，决策树可以把任意数据都处理得很好。）

数据的无量纲化可以是线性的，也可以是非线性的。线性的无量纲化包括中心化（Zero-centered或者Meansubtraction）处理和缩放处理（Scale）。

中心化的本质是让所有记录减去一个固定值，即让数据样本数据平移到某个位置。

缩放的本质是通过除以一个固定值，将数据固定在某个范围之中，取对数也算是一种缩放处理。

1.preprocessing.MinMaxScaler归一化

当数据(x)按照最小值中心化后，再按极差（最大值 - 最小值）缩放，数据移动了最小值个单位，并且会被收敛到[0,1]之间，而这个过程，就叫做数据归一化(Normalization，又称Min-Max Scaling)。

注意，Normalization是归一化，不是正则化，真正的正则化是regularization，不是数据预处理的一种手段。归一化之后的数据服从正态分布，公式如下：

                                                

在sklearn当中，我们使用preprocessing.MinMaxScaler来实现这个功能。MinMaxScaler有一个重要参数，feature_range，控制我们希望把数据压缩到的范围，默认是[0,1]。

#归一化的实现
from sklearn.preprocessing import MinMaxScaler
data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]
data

 

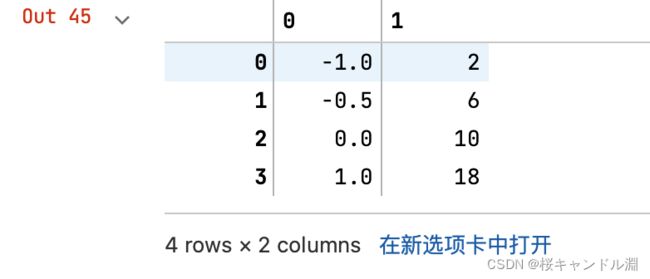
#如果换成表是什么样子？
import pandas as pd
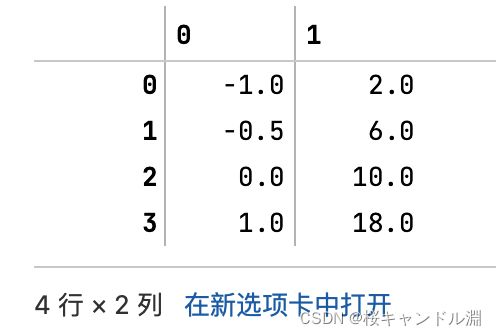
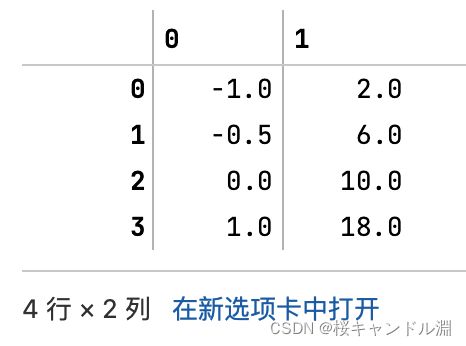
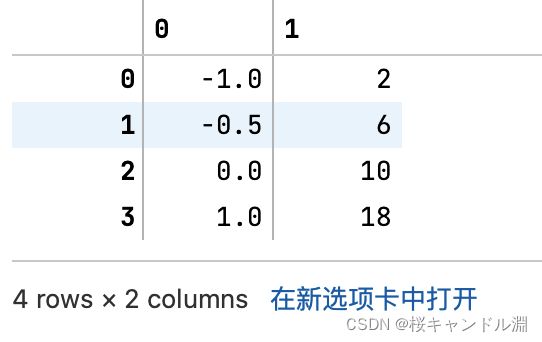
pd.DataFrame(data)

 

#实现归一化
scaler = MinMaxScaler() #实例化
scaler = scaler.fit(data) #fit，在这里本质是生成min(x)和max(x)
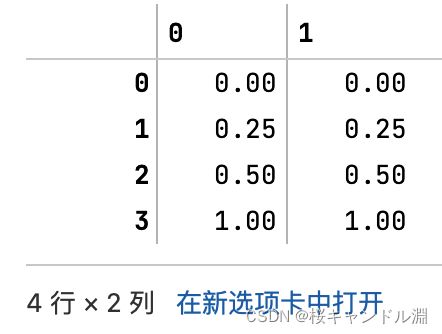
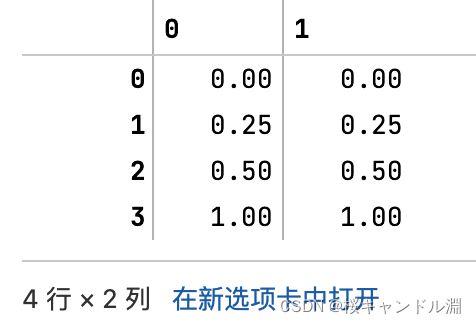
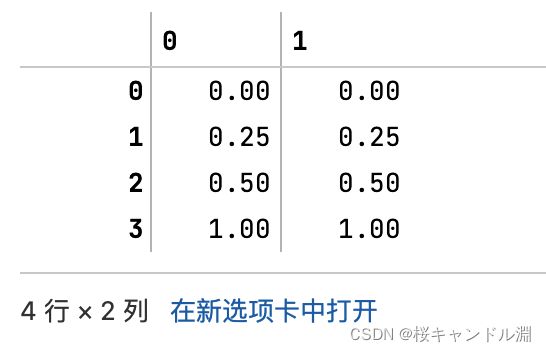
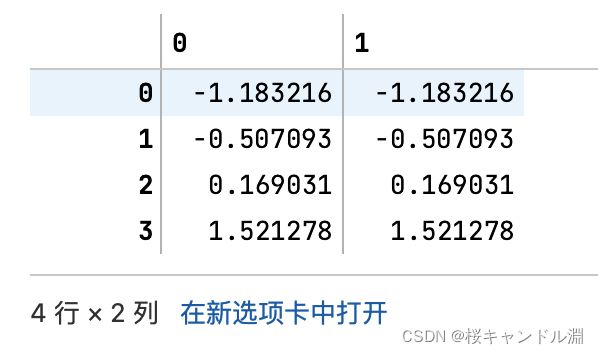
result = scaler.transform(data) #通过接口导出结果
#生成已经归一化完毕的数据，是一个矩阵
#这个矩阵和我们上面的那个原来的矩阵都是四行两列的
#其归一化的球阀就是对每一列中的每一个数据减去这一列数据中的最小值然后除以这一列当中的最大值减去这一列当中的最小值
#比方说我们下面的第0列中的[0][0]就是这一列中的最小值，所以是-1
#第0列中的[0][3]是这一列当中的最大值，所以是1
#最大值减去最小值就是2
#所以我们第0列的[0][1]就是将原本[0][1]的数据-0.5，减去-1.0得到0.5，然后用0.5除以2，得到了0.25
#
result

#上面的fit和transform完全可以被这一行代替
result_ = scaler.fit_transform(data) #训练和导出结果一步达成
result_

 

scaler.inverse_transform(result) #将归一化后的结果逆转，也就是返回我们原本的数据

①归一化到[0,1]以外的范围

#使用MinMaxScaler的参数feature_range实现将数据归一化到[0,1]以外的范围中
data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]
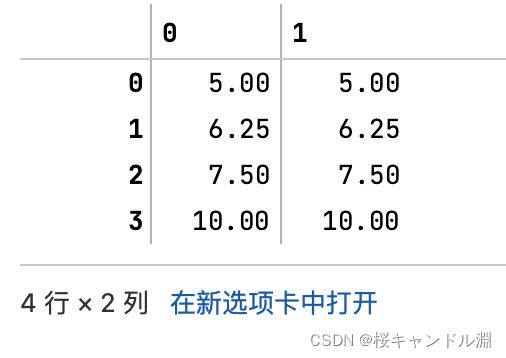
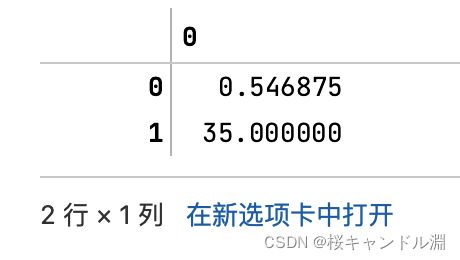
scaler = MinMaxScaler(feature_range=[5,10]) #依然实例化，指定将feature_range的归一化的范围限定在5-10之间
result = scaler.fit_transform(data) #fit_transform一步导出结果
result

 

#当X中的特征数量非常多的时候，fit会报错并表示，数据量太大了我计算不了
#此时使用partial_fit作为训练接口
#实例化后的模型.partial_fit(传入的数据)
#scaler = scaler.partial_fit(data)

②用numpy实现归一化

#用numpy实现归一化
import numpy as np
X = np.array([[-1, 2], [-0.5, 6], [0, 10], [1, 18]])
#归一化
#对每一列（axis=0逐行按列进行运算）的数据执行下面的代码，也就是我们归一化的公式
#(x-最小值)/极差（最大值-最小值）
X_nor = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_nor

③逆转归一化

#逆转归一化
#逆归一化就是归一化之后的数据乘以原来数据的极差，然后加上原来每一列数据中的极小值
X_returned = X_nor * (X.max(axis=0) - X.min(axis=0)) + X.min(axis=0)
X_returned

2.preprocessing.StandardScaler标准化

#数据的标准化
#让所有的数据减去一个值，从而让整个图像平移到某一个位置，例子：正太分布的数据都减掉其均值，将整个图像平移到以y轴为中心的图像

preprocessing.StandardScaler
当数据(x)按均值(μ)中心化后，再按标准差(σ)缩放，数据就会服从为均值为0，方差为1的正态分布（即标准正态分布），而这个过程，就叫做数据标准化(Standardization，又称Z-score normalization)，公式如下：

                        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​     
（数据减去均值再除以标准差来缩放就能将我们的数据变成均值为0，方差为1的标准正态分布了）

#导入相应的库
#standardscaler就是用于标准化数据的库
from sklearn.preprocessing import StandardScaler
#这里的数据依然是这两组数据，跟我们上面的数据是一模一样的
data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]
data=pd.DataFrame(data)
data

scaler = StandardScaler() #实例化
scaler.fit(data) #fit，本质是生成均值和方差

#这里的mean_所得出的是分别求出这两列的平均值
#不像numpy中使用min,max的时候需要传入轴向的参数，
#sklearn自动就会知道你想算的数据是按列计算的均值和方差
#因为没人会把一整行的数据，也就是一条记录的数据，压缩到0到1直接，或者是服从正太状态分布，这是没有意义的
#我们所要压缩的是我们的特征
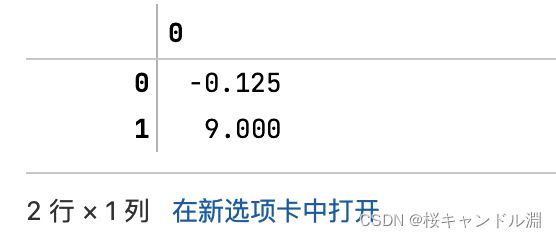
scaler.mean_ #查看均值的属性mean_

 

#分别求出这两列的方差
scaler.var_ #查看方差的属性var_

 

x_std = scaler.transform(data) #通过接口导出结果
x_std
#我们注意到两类数据导出了相同的值，因为这两列数据虽然大小不同，但是其两列数据的分布是一样的，所以它们在被标准化之后，数据也会一模一样

 核实是不是标准正态分布

x_std.mean() #导出的结果是一个数组，用mean()查看均值

 

x_std.std() #用std()查看方差

 

scaler.fit_transform(data) #使用fit_transform(data)一步达成结果
#逆转标准化，返回原本的结果
scaler.inverse_transform(x_std) #使用inverse_transform逆转标准化

3.总结

对于StandardScaler和MinMaxScaler来说，空值NaN会被当做是缺失值，在fit的时候忽略，在transform的时候保持缺失NaN的状态显示。并且，尽管去量纲化过程不是具体的算法，但在fit接口中，依然只允许导入至少二维数组，一维数组导入会报错。

通常来说，我们输入的X会是我们的特征矩阵，现实案例中特征矩阵不太可能是一维所以不会存在这个问题。

（通常来说我们现实输入的特征矩阵都是一维以上的数据）

StandardScaler和MinMaxScaler选哪个？

看情况。大多数机器学习算法中，会选择StandardScaler来进行特征缩放，因为MinMaxScaler对异常值非常敏感。在PCA，聚类，逻辑回归，支持向量机，神经网络这些算法中，StandardScaler往往是最好的选择。

MinMaxScaler在不涉及距离度量、梯度、协方差计算以及数据需要被压缩到特定区间时使用广泛，比如数字图像处理中量化像素强度时，都会使用MinMaxScaler将数据压缩于[0,1]

建议先试试看StandardScaler，效果不好换MinMaxScaler。

除了StandardScaler和MinMaxScaler之外，sklearn中也提供了各种其他缩放处理（中心化只需要一个pandas广播一下减去某个数就好了，因此sklearn不提供任何中心化功能）。比如，在希望压缩数据，却不影响数据的稀疏性时（不影响矩阵中取值为0的个数时），我们会使用MaxAbsScaler（只压缩，不中心化）；在异常值多，噪声非常大时，我们可能会选用分位数来无量纲化，此时使用RobustScaler。更多详情请参考以下列表

二、处理缺失值

机器学习和数据挖掘中所使用的数据，永远不可能是完美的。很多特征，对于分析和建模来说意义非凡，但对于实际收集数据的人却不是如此，因此数据挖掘之中，常常会有重要的字段缺失值很多，但又不能舍弃字段的情况。因此，数据预处理中非常重要的一项就是处理缺失值。

import pandas as pd
#这里的index_col=0就是将第0列作为索引，如果不写的话，就会把我们数据集中第一列的索引当成是一列特征，然后重新生成新的一列索引
data = pd.read_csv(r"/Users/Narrativedata.csv",index_col=0)
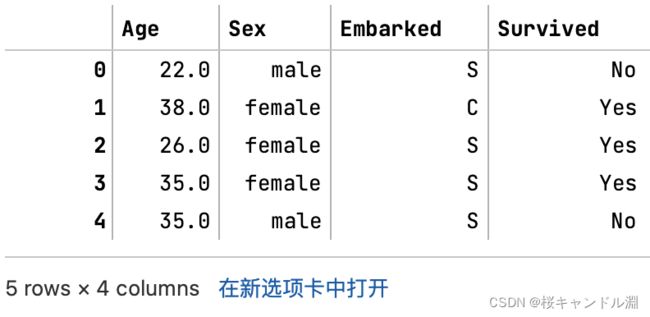
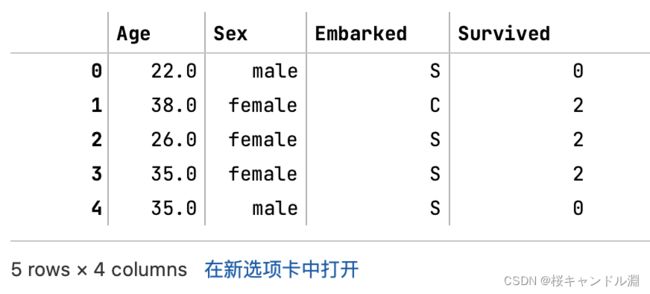
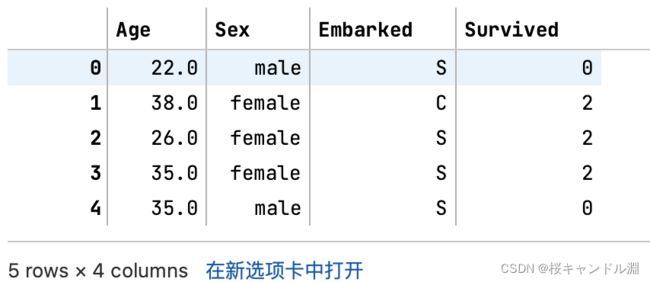
data.head()

 

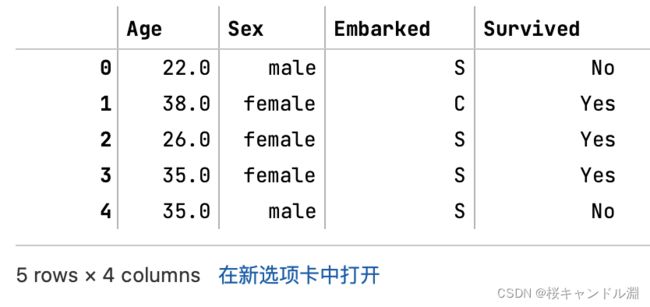
#观察一下我们的数据集
data.head(20)

 

1.impute.SimpleImputer

class sklearn.impute.SimpleImputer (
        missing_values=nan, 
        strategy=’mean’, 
        fill_value=None, 
        verbose=0,
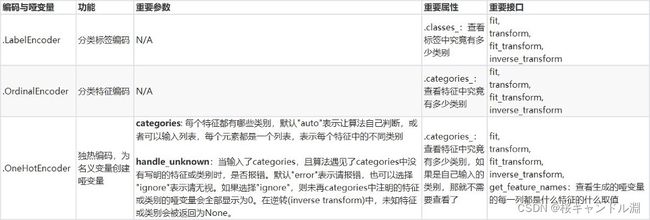
        copy=True)

在讲解随机森林的案例时，我们用这个类和随机森林回归填补了缺失值，对比了不同的缺失值填补方式对数据的影响。这个类是专门用来填补缺失值的。它包括四个重要参数：

参数	含义&输入
missing_values	告诉SimpleImputer，数据中的缺失值长什么样，默认空值np.nan
strategy	我们填补缺失值的策略，默认均值。    输入“mean”使用均值填补（仅对数值型特征可用）输入“median"用中值填补（仅对数值型特征可用） 输入"most_frequent”用众数填补（对数值型和字符型特征都可用） 输入“constant"表示请参考参数“fill_value"中的值（对数值型和字符型特征都可用）
fill_value	当参数startegy为”constant"的时候可用，可输入字符串或数字表示要填充的值，常用0
copy	默认为True，将创建特征矩阵的副本，反之则会将缺失值填补到原本的特征矩阵中去。

 

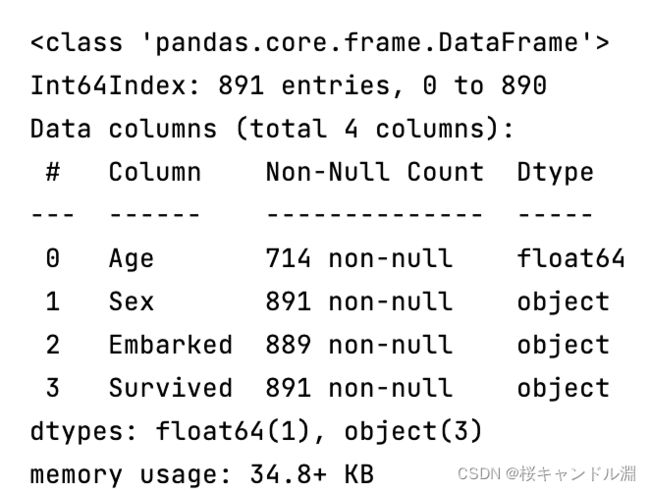
data.info()
#w我们发现年龄和登仓有缺失值

#填补年龄
#loc是按照索引的名字进行切片
#.values取出其中的值
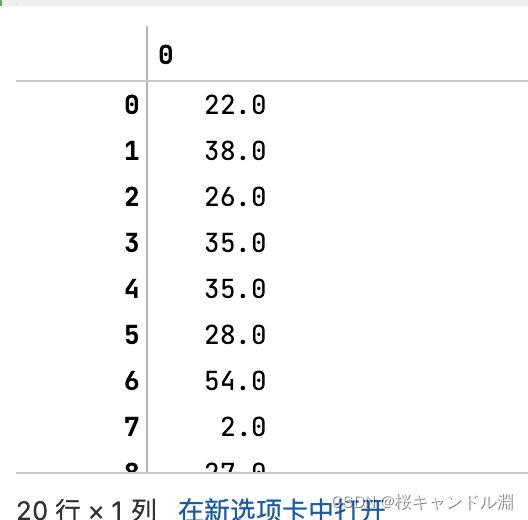
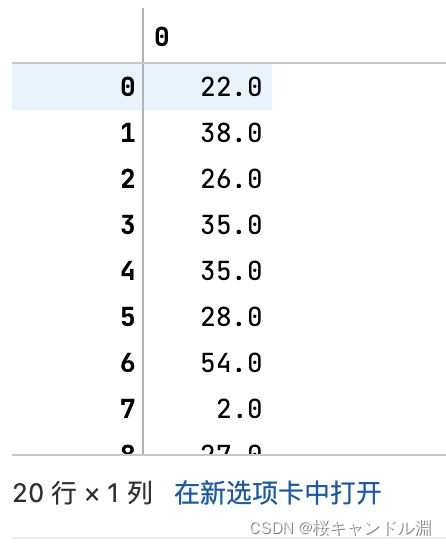
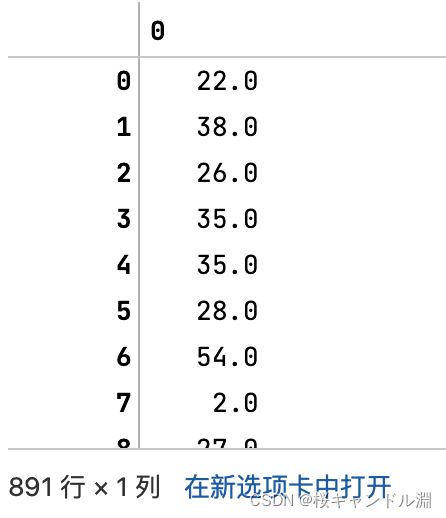
Age = data.loc[:,"Age"].values.reshape(-1,1) #sklearn当中特征矩阵必须是二维，因为我们扥数据需要fit进入我们的模型
#输入reshape(-1,1)就能够将我们的一维的数据转换成二维的

Age[:20]

 

①分别用平均值，中位数，0值填充空值 

from sklearn.impute import SimpleImputer
imp_mean = SimpleImputer() #实例化，默认均值填补
imp_median = SimpleImputer(strategy="median") #用中位数填补
imp_0 = SimpleImputer(strategy="constant",fill_value=0) #用0填补

imp_mean = imp_mean.fit_transform(Age) #fit_transform一步完成调取结果
imp_median = imp_median.fit_transform(Age)
imp_0 = imp_0.fit_transform(Age)
#会直接返回填好缺失值的数据

#年龄一般选择均值进行填补
imp_mean[:20]

 

#中位数的填补
imp_median[:20]

#用0值填补
imp_0[:20]

 

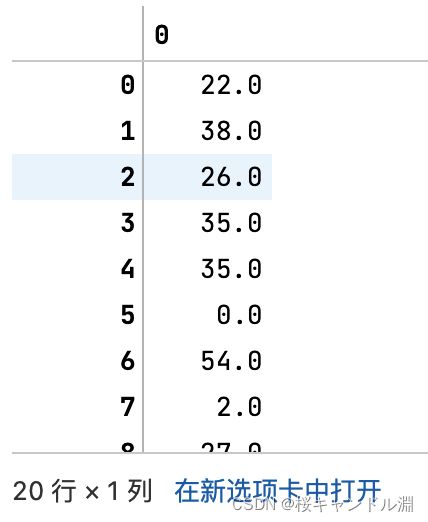
#在这里我们使用中位数填补Age
data.loc[:,"Age"] = imp_median
data.info()

②使用众数填补缺失值

#使用众数填补Embarked
Embarked = data.loc[:,"Embarked"].values.reshape(-1,1)
Embarked

#most_frequent就是使用频率最高的数据进行填补，是可以对文字类型的数据进行频度处理的
imp_mode = SimpleImputer(strategy = "most_frequent")
data.loc[:,"Embarked"] = imp_mode.fit_transform(Embarked)
data.info()

 

③用numpy或者pandas填补缺失值

#用Pandas和Numpy进行填补其实更加简单
import pandas as pd
data_ = pd.read_csv(r"/Users/yangkailiang/Documents/【机器学习】菜菜的sklearn课堂(1-12全课)/03数据预处理和特征工程/Narrativedata.csv",index_col=0)
data_.head()

 

data_.loc[:,"Age"] = data_.loc[:,"Age"].fillna(data_.loc[:,"Age"].median())
#.fillna 在DataFrame里面直接进行填补，fillna中填写你期望给空值填补的数据
data_.loc[:,"Age"].isnull().sum()

 

data_.dropna(axis=0,inplace=True)
#.dropna(axis=0)删除所有有缺失值的行，.dropna(axis=1)删除所有有缺失值的列
#参数inplace，为True表示在原数据集上进行修改，为False表示生成一个复制对象，不修改原数据，默认False

data_.info()

三、编码与哑变量

处理分类型特征：编码与哑变量
在机器学习中，大多数算法，譬如逻辑回归，支持向量机SVM，k近邻算法等都只能够处理数值型数据，不能处理文字，在sklearn当中，除了专用来处理文字的算法，其他算法在fit的时候全部要求输入数组或矩阵，也不能够导入文字型数据

（其实手写决策树和普斯贝叶斯可以处理文字，但是sklearn中规定必须导入数值型）。
然而在现实中，许多标签和特征在数据收集完毕的时候，都不是以数字来表现的。比如说，学历的取值可以是[“小学”，“初中”，“高中”，“大学”]，付费方式可能包含[“支付宝”，“现金”，“微信”]等等。在这种情况下，为了让数据适应算法和库，我们必须将数据进行编码，即是说，将文字型数据转换为数值型。

1.preprocessing.LabelEncoder标签编码

#preprocessing.LabelEncoder：标签专用，能够将分类转换为分类数值
#Label就是标签，encoder就是编码

from sklearn.preprocessing import LabelEncoder
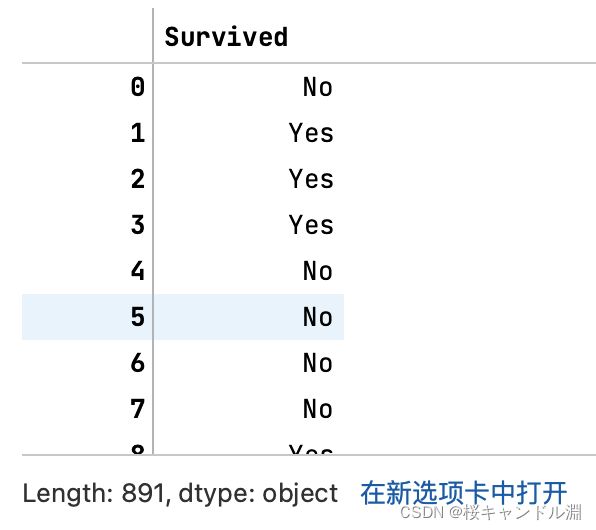
y = data.iloc[:,-1] #要输入的是标签，不是特征矩阵，所以允许一维
y

 

le = LabelEncoder() #实例化
le = le.fit(y) #导入数据
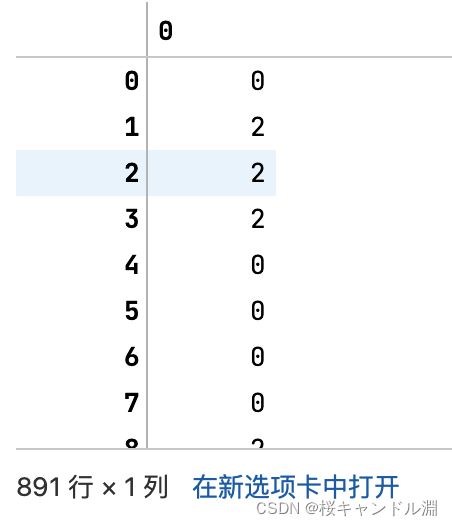
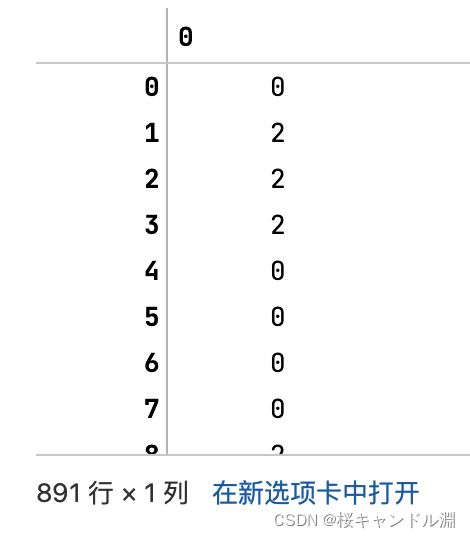
label = le.transform(y) #transform接口调取结果
label
#我们观察到我们的数据变成了0，1，2

 

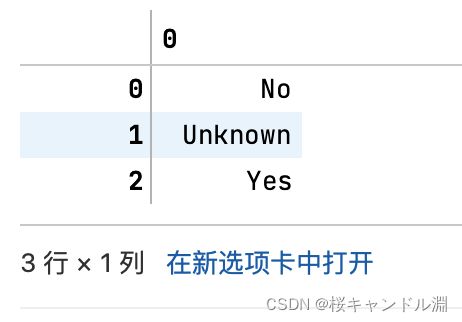
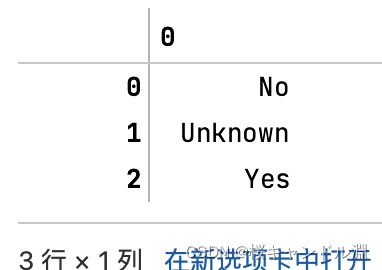
le.classes_ #属性.classes_查看标签中究竟有多少类别
#我们发现除了No,Yes还有unknown。
#也就是说我们的tranform也可以处理三分类

 

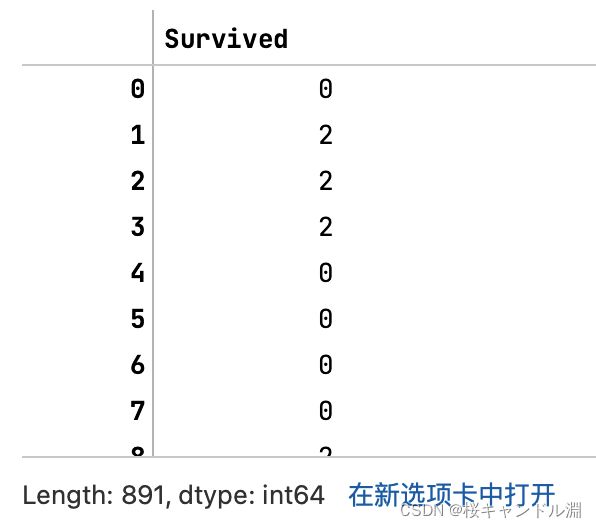
label #查看获取的结果label

 

le.fit_transform(y) #也可以直接fit_transform一步到位

---

①逆转编码

le.inverse_transform(label) #使用inverse_transform可以逆转

---

data.iloc[:,-1] = label #让标签等于我们运行出来的结果
data.head()

#更加精简的写法：
from sklearn.preprocessing import LabelEncoder
data.iloc[:,-1] = LabelEncoder().fit_transform(data.iloc[:,-1])
data.iloc[:,-1]

2.preprocessing.OrdinalEncoder特征编码

#preprocessing.OrdinalEncoder：特征专用，能够将分类特征转换为分类数值
from sklearn.preprocessing import OrdinalEncoder
#接口categories_对应LabelEncoder的接口classes_，一模一样的功能
data_ = data.copy()
data_

 

data_.head()

 

#这个ordinalencoder中的categories和我们上面的labelencoder中的classes_是比较相似的
#就是帮你查看每个特征中有多少个类别。
OrdinalEncoder().fit(data_.iloc[:,1:-1]).categories_

#将data中的第一列到最后一列全部都转换成对应的数据
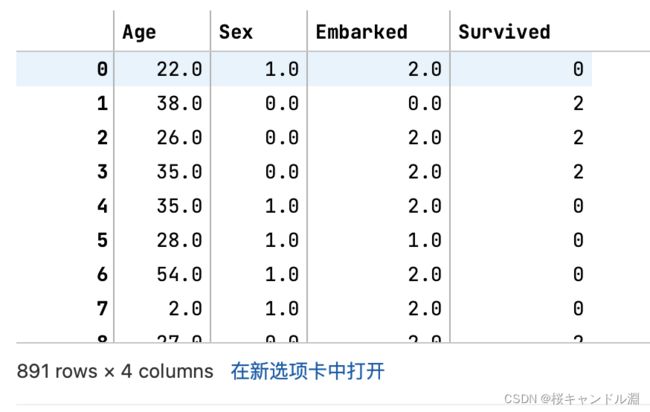
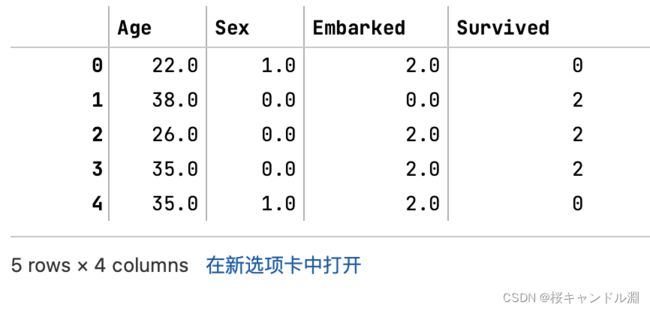
data_.iloc[:,1:-1] = OrdinalEncoder().fit_transform(data_.iloc[:,1:-1])
data_.head()

 

3.preprocessing.OneHotEncoder独热编码

preprocessing.OneHotEncoder：独热编码，创建哑变量
我们刚才已经用OrdinalEncoder把分类变量Sex和Embarked都转换成数字对应的类别了。在舱门Embarked这一列中，我们使用[0,1,2]代表了三个不同的舱门，然而这种转换是正确的吗？
我们来思考三种不同性质的分类数据：
1） 舱门（S，C，Q）
三种取值S，C，Q是相互独立的，彼此之间完全没有联系，表达的是S≠C≠Q的概念。这是名义变量。
2） 学历（小学，初中，高中）
三种取值不是完全独立的，我们可以明显看出，在性质上可以有高中>初中>小学这样的联系，学历有高低，但是学历取值之间却不是可以计算的，我们不能说小学 + 某个取值 = 初中。这是有序变量。
3） 体重（>45kg，>90kg，>135kg）
各个取值之间有联系，且是可以互相计算的，比如120kg - 45kg = 90kg，分类之间可以通过数学计算互相转换。这是有距变量。
然而在对特征进行编码的时候，这三种分类数据都会被我们转换为[0,1,2]，这三个数字在算法看来，是连续且可以计算的，这三个数字相互不等，有大小，并且有着可以相加相乘的联系。所以算法会把舱门，学历这样的分类特征，都误会成是体重这样的分类特征。这是说，我们把分类转换成数字的时候，忽略了数字中自带的数学性质，所以给算法传达了一些不准确的信息，而这会影响我们的建模。

类别OrdinalEncoder可以用来处理有序变量，但对于名义变量，我们只有使用哑变量的方式来处理，才能够尽量向算法传达最准确的信息：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​

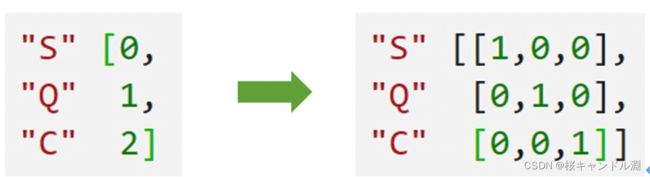
这样的变化，让算法能够彻底领悟，原来三个取值是没有可计算性质的，是“有你就没有我”的不等概念。在我们的数据中，性别和舱门，都是这样的名义变量。因此我们需要使用独热编码，将两个特征都转换为哑变量。

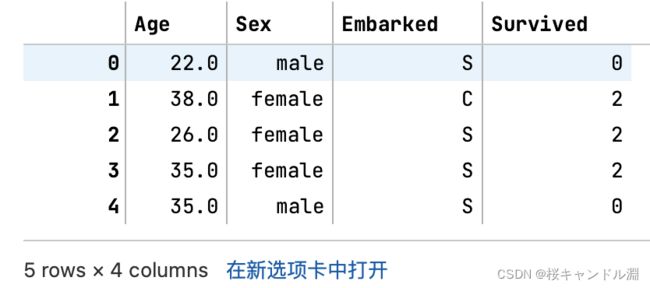
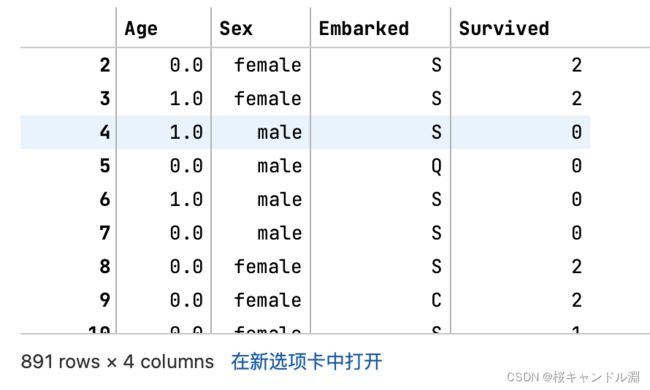
data.head()

 

 

from sklearn.preprocessing import OneHotEncoder
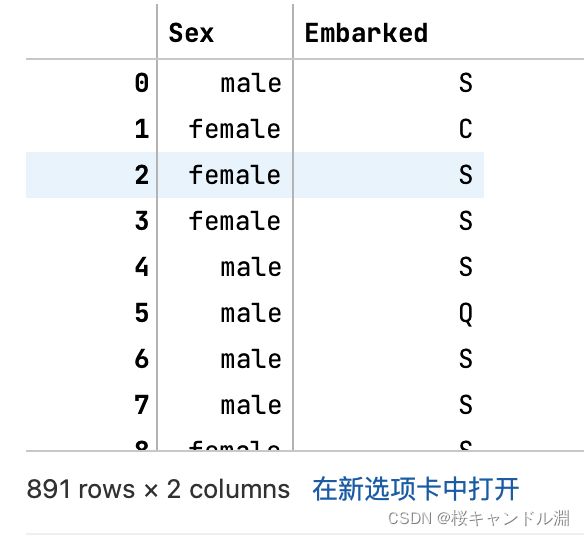
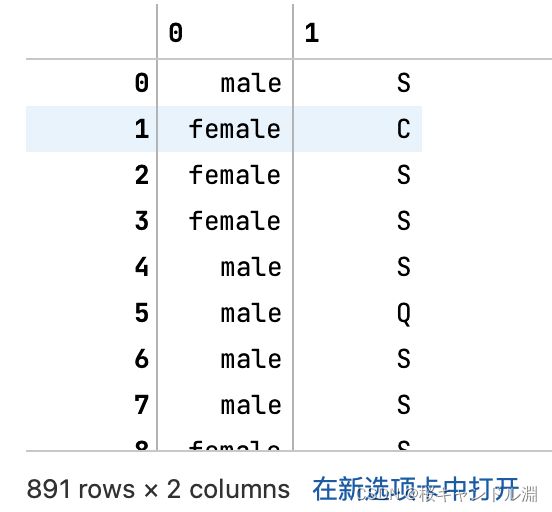
X = data.iloc[:,1:-1]
X

 

#在sklearn0.19版本中需要手动传入categories也就是每一列的数据
#在sklearn0.20版本之后可以传入参数'auto'让其自己去判断有几个数据
enc = OneHotEncoder(categories='auto').fit(X)
#toarray请将这个结果转化成一个数组
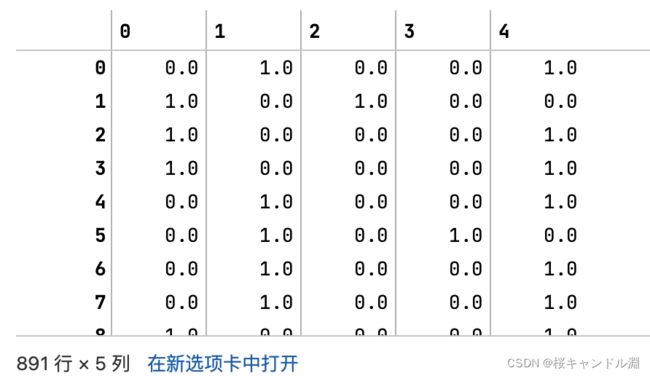
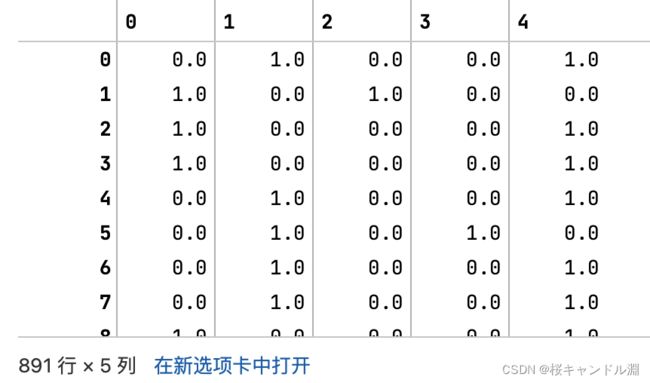
result = enc.transform(X).toarray()
result
#为什么下面的结果会有5列？
#因为我们让我们的独热编码转换了两个特征
#第一个特征是性别，在性别这个特征中，我们有两种不同的类别，所以男一列，女一列
#第二个特征是舱门的编号，舱门的编号有SQC三种不同的值，所以又有三列
#所以两个特征中总共有五个类别，所以一共有五列哑变量

 

#如果不toarray的话，会生成下面这个东西
#也就是一个稀疏矩阵对象（也就是由0和1组成的矩阵）
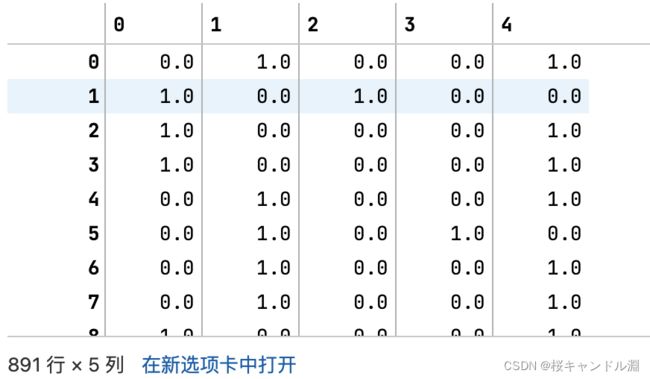
enc.transform(X)

#直接一步到位
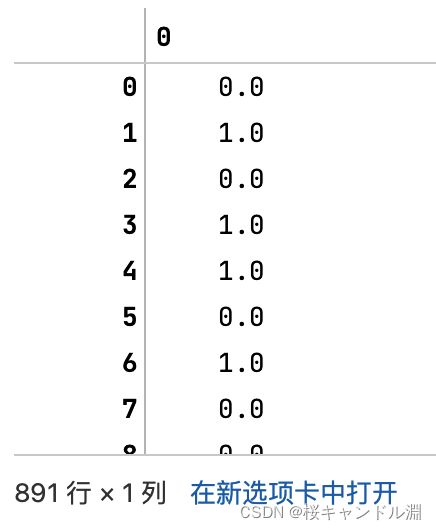
OneHotEncoder(categories='auto').fit_transform(X).toarray()

①还原原矩阵

#依然可以还原
pd.DataFrame(enc.inverse_transform(result))

②获取稀疏矩阵对应的列名

#在我们fit完成之后的模型上，加上方法get_feature_names_out()
#就会返回每一个稀疏矩阵中列的名字
enc.get_feature_names_out()

 

result

 

result.shape

③合并数据

#将我们新生成的独热编码表跟我们之前的原表拼接起来
#axis=1,表示跨行进行合并，也就是将量表左右相连，如果是axis=0，就是将量表上下相连
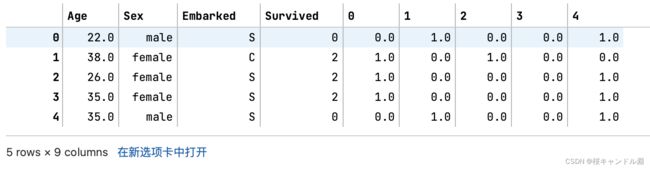
#下面的代码就是将我们新生成的独热编码加在我们原来的表的右边
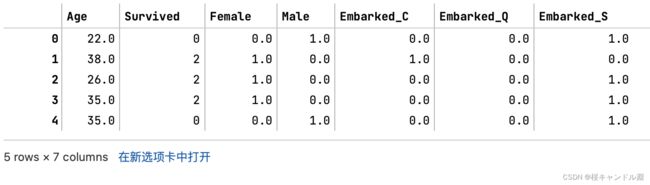
newdata = pd.concat([data,pd.DataFrame(result)],axis=1)

newdata.head()

#将原来的旧的列删掉
#axis=1也就是跨行删除，也就是删除一列
newdata.drop(["Sex","Embarked"],axis=1,inplace=True)

#重新指定索引
newdata.columns =["Age","Survived","Female","Male","Embarked_C","Embarked_Q","Embarked_S"]
newdata.head()

特征可以做哑变量，标签也可以吗？可以，使用类sklearn.preprocessing.LabelBinarizer可以对做哑变量，许多算法都可以处理多标签问题（比如说决策树），但是这样的做法在现实中不常见。

数据类型以及常用的统计量 

 

四、二值化与分段

1.sklearn.preprocessing.Binarizer二值化

处理连续型特征：二值化与分段
根据阈值将数据二值化（将特征值设置为0或1），用于处理连续型变量。大于阈值的值映射为1，而小于或等于阈值的值映射为0。默认阈值为0时，特征中所有的正值都映射到1。二值化是对文本计数数据的常见操作，分析人员可以决定仅考虑某种现象的存在与否。它还可以用作考虑布尔随机变量的估计器的预处理步骤（例如，使用贝叶斯设置中的伯努利分布建模）。

①二值化特征 

#将年龄二值化
data_2 = data.copy()
data_2

 

#导入二值化的模块
from sklearn.preprocessing import Binarizer
X = data_2.iloc[:,0].values.reshape(-1,1) #类为特征专用，所以不能使用一维数组
X

 

#实例化我们的Binarizer，然后传入的threshold也就是我们的阈值
#在下面的代码中就是年龄超过30岁的划分为1，少于30岁的划分为0
#实例化之后直接fit_transform，一步到位
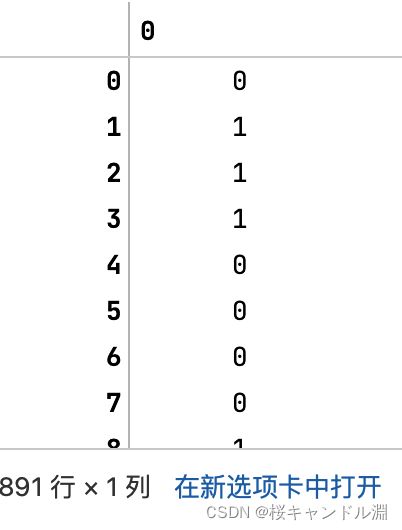
transformer = Binarizer(threshold=30).fit_transform(X)
transformer
#我们从下面的数据可以观察到数据全部都变成了0和1

 

#将二值化之后的数据放回去
data_2.iloc[:,0]=transformer
data_2

②二值化标签

#二值化我们的标签
#
Y = data_2.iloc[:,3].values.reshape(-1,1)
Y

 

le.classes_

 

#由于在泰坦尼克号海难中失踪了和死亡，其实没有太大的区别，所以我们就将这两个标签归为一类
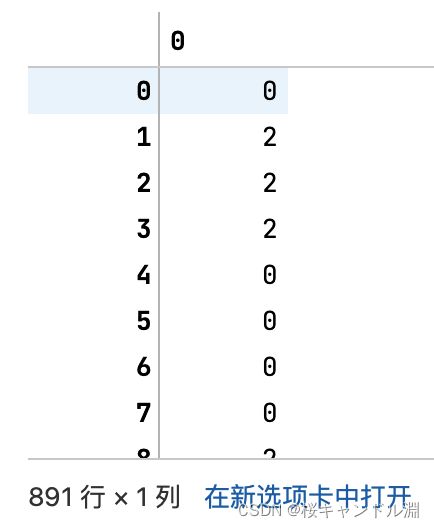
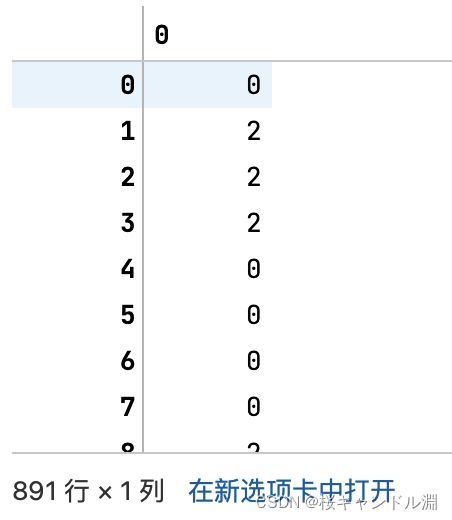
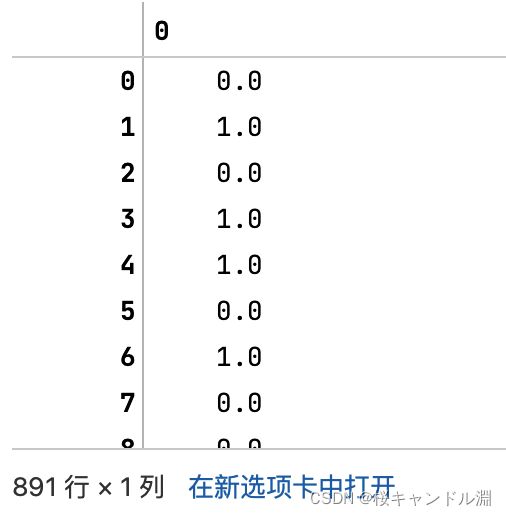
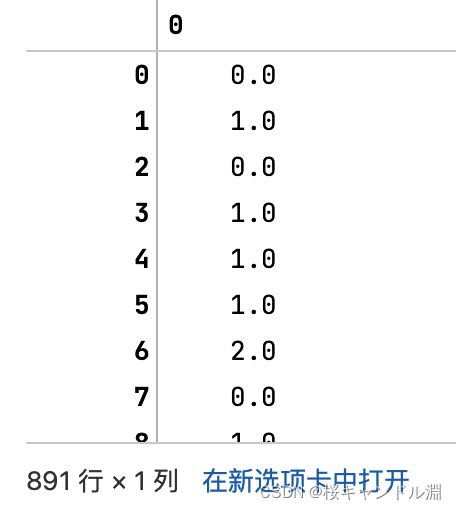
transformer_Y=Binarizer(threshold=1).fit_transform(Y)
transformer_Y
#这时我们就发现0和1也就是No和Unknown群不都变成了0，只有Yes，变成了1，我们成功实现了二值化

 

2.preprocessing.KBinsDiscretizer分箱

（除了二值化之外，我们还可以对我们的连续性变量进行分箱操作）
（分箱就是比方说将0-10岁的划分为儿童，10-18岁为青年，19-30为成人等等之类的划分，也就是不止两个值，并且在分箱之后，还可以按照其顺序进行编码）
这是将连续型变量划分为分类变量的类，能够将连续型变量排序后按顺序分箱后编码。总共包含三个重要参数：

参数	含义&输入
n_bins	每个特征中分箱的个数，默认5，一次会被运用到所有导入的特征
encode	编码的方式，默认“onehot”                                                                                 "onehot"：做哑变量，之后返回一个稀疏矩阵，每一列是一个特征中的一个类别，含有该类别的样本表示为1，不含的表示为0                                                                  “ordinal”：每个特征的每个箱都被编码为一个整数，返回每一列是一个特征，每个特征下含 有不同整数编码的箱的矩阵 "onehot-dense"：做哑变量，之后返回一个密集数组。
strategy	用来定义箱宽的方式，默认"quantile"                                   "uniform"：表示等宽分箱，即每个特征中的每个箱的最大值之间的差为   (特征.max()                    -                    特征.min())/(n_bins) "quantile"：表示等位分箱，即每个特征中的每个箱内的样本数量都相同 "kmeans"：表示按聚类分箱，每个箱中的值到最近的一维k均值聚类的簇心得距离都相同

最常用的是等位分箱

#导入分箱相关的库
from sklearn.preprocessing import KBinsDiscretizer
#取出我们的年龄模块（连续型数据）
#reshape升维
X = data.iloc[:,0].values.reshape(-1,1)
X

 

#实例化分箱，分成3箱，编码的方式是ordinal，有几个特征就返回几列，每一列当中都是每一个特征的类别
#strategy=“uniform”就是按照等宽进行分箱
est = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='uniform')
est.fit_transform(X)
#我们看到返回的了一列，也就是我们上面年龄的对应的分享结果，数据分别为0，1，2，也就是对应的三个箱子

验证分箱结果 

#查看转换后分的箱：变成了一列中的三箱
#ravel()是降维函数，将我上面二维的数据降成一维，然后将其转化成一个集合
#set因为是会自动去除重复的数据的，所以我们可以看出到底有几个不同的分箱
set(est.fit_transform(X).ravel())

 

#这里与上面不同的是，我们将编码方式转化成了独热编码，其他都没有变化
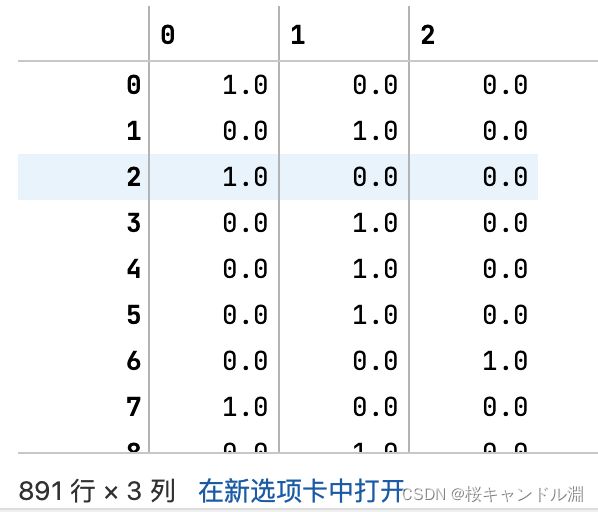
est = KBinsDiscretizer(n_bins=3, encode='onehot', strategy='uniform')
#查看转换后分的箱：变成了哑变量
est.fit_transform(X).toarray()
#我们看到其返回了三列稀疏矩阵，因为我们让它分成了三箱，所以它在哪一个箱子中是1就代表着它属于哪一箱