Deformable ConvNets可变形卷积
论文:Deformable Convolutional Networks(CVPR 2017)
文章目录
-
- 针对问题
- 可变形卷积
- Deformable RoI Pooling
- 实验结果对比
- 可变形卷积Pytorch实现
- 补充
- 参考文献
针对问题
如何应对几何形变问题(尺度,姿态,视点和部件变形等),常用方法:
- 假设目标分布已知的情况下,通过增加具有期望变化的样本,
- 或者设计invariant features和算法
但上述方法都难以应对复杂的或新的变化,文中通过在卷积层和RoI pooling层中引入offset以提高网络的灵活性,能够更好地覆盖不同尺度和形状的目标,使网络更专注于目标区域,提取到的特征更加丰富
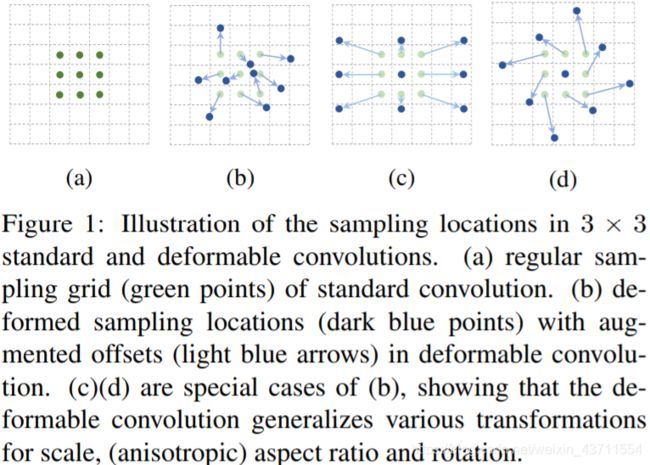
可变形卷积
3 × 3 3\times3 3×3 卷积核 , R \mathscr{R} R for Regular Grid
( − 1 , − 1 ) ( 0 , − 1 ) ( 1 , − 1 ) ( − 1 , 0 ) ( 0 , 0 ) ( 1 , 0 ) ( − 1 , 1 ) ( 0 , 1 ) ( 1 , 1 ) \begin{matrix} (-1,-1)&(0,-1)&(1,-1)\\ (-1,0)&(0,0)&(1,0)\\ (-1,1)&(0,1)&(1,1) \end{matrix} (−1,−1)(−1,0)(−1,1)(0,−1)(0,0)(0,1)(1,−1)(1,0)(1,1)
普通卷积
y ( p 0 ) = ∑ p n ∈ R w ( p n ) ⋅ x ( p 0 + p n ) y(p_0)=\sum\limits_{p_n\in \mathscr{R}}\ w(p_n)\cdot x(p_0+p_n) y(p0)=pn∈R∑ w(pn)⋅x(p0+pn)
可变形卷积增加了可以学习的坐标偏移量 Δ p n \Delta p_n Δpn
y ( p 0 ) = ∑ p n ∈ R w ( p n ) ⋅ x ( p 0 + p n + Δ p n ) ⏟ 插值得到偏移坐标处像素值 \begin{aligned} y(p_0)=\sum\limits_{p_n\in \mathscr{R}}\ w(p_n)\cdot \underbrace{x(p_0+p_n+\Delta p_n)}_{\text{插值得到偏移坐标处像素值}} \end{aligned} y(p0)=pn∈R∑ w(pn)⋅插值得到偏移坐标处像素值 x(p0+pn+Δpn)
上式可以看出:变形的其实不是卷积核,而是特征图,普通卷积作用在变形的特征图上达到了变形卷积的效果
计算梯度:
∂ y ( p 0 ) ∂ Δ p n = ∑ p n ∈ R w ( p n ) ⋅ ∂ x ( p 0 + p n + Δ p n ) ∂ Δ p n = ∑ p n ∈ R [ w ( p n ) ⋅ ∑ q ∂ G ( q , p 0 + p n + Δ p n ) ∂ Δ p n ⋅ x ( q ) ] \begin{aligned} \frac{\partial\ \boldsymbol{y}(p_0)}{\partial\ \Delta\ \boldsymbol{p}_n} &=\sum\limits_{\boldsymbol{p}_n\in \mathscr{R}}\ \boldsymbol{w}(\boldsymbol{p}_n)\cdot \frac{\partial\ \boldsymbol{x}(\boldsymbol{p}_0+\boldsymbol{p}_n+\Delta \boldsymbol{p}_n)}{\partial\ \Delta\boldsymbol{p}_n} \\ &=\sum\limits_{\boldsymbol{p}_n\in \mathscr{R}}\ \left[\boldsymbol{w}(\boldsymbol{p}_n)\cdot \sum\limits_q\ \frac{\partial\ G(\boldsymbol{q},\boldsymbol{p}_0+\boldsymbol{p}_n+\Delta \boldsymbol{p}_n)}{\partial\ \Delta \boldsymbol{p}_n}\cdot \boldsymbol{x}(\boldsymbol{q})\right] \end{aligned} ∂ Δ pn∂ y(p0)=pn∈R∑ w(pn)⋅∂ Δpn∂ x(p0+pn+Δpn)=pn∈R∑ [w(pn)⋅q∑ ∂ Δpn∂ G(q,p0+pn+Δpn)⋅x(q)]
Δ p n \Delta p_n Δpn通常都是小数,而图像是一个一个离散像素点,可以用双线性差值进行差值计算出该处像素值,可变形卷积示意图如下:
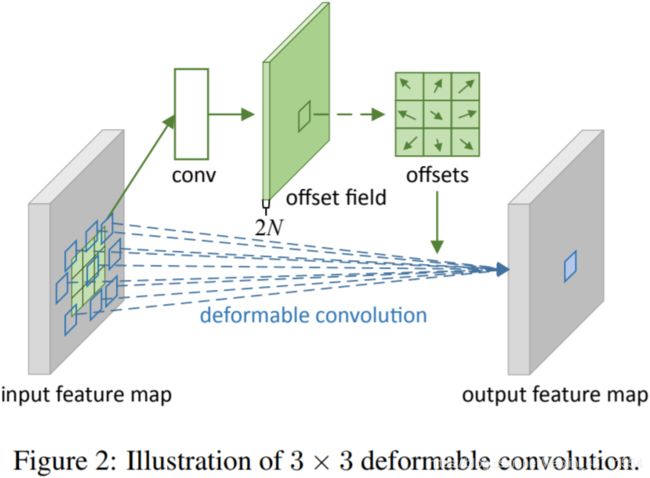
可变形卷积步骤
- 输入 【 B ∗ H ∗ W ∗ C 】 【B*H*W*C】 【B∗H∗W∗C】经过普通卷积(same)得到输出 【 B ∗ H ∗ W ∗ ( 2 ⋅ n ⋅ n ) 】 【B*H*W*(2\cdot n\cdot n)】 【B∗H∗W∗(2⋅n⋅n)】, n n n 表示卷积核尺寸,乘以2表示每个像素都有 x 、 y x、y x、y两个方向的偏移量,其实就是相对偏移坐标
- 将1中得到的相对偏移坐标与原坐标相加,即得到各个像素偏移后的位置(要将位置限定在原图坐标范围内,不能超出图片范围)
- 因为图像都是由离散的一个一个像素组成,而求得的偏移位置是浮点数,需要用到双线性插值的方法该位置对应像素值(根据该点周围的四个点计算: 【 c e i l ( x ) , c e i l ( y ) 】 【ceil(x),ceil(y)】 【ceil(x),ceil(y)】、 【 f l o o r ( x ) , c e i l ( y ) 】 【floor(x),ceil(y)】 【floor(x),ceil(y)】、 【 c e i l ( x ) , f l o o r ( y ) 】 【ceil(x),floor(y)】 【ceil(x),floor(y)】、 【 f l o o r ( x ) , f l o o r ( y ) 】 【floor(x),floor(y)】 【floor(x),floor(y)】,梯度回传也是根据这四个点)
- 计算得到变换后的特征图作输出
Deformable Group
注意:如果按照上面的方法计算的话,特征图中同一个像素点的不同Channel有不一样的偏移量。源码中num_deformable_group变量,其作用是将输入沿Channel Axis分割成几个部分(Group),同一个Group的Channel共享offset。设置Goup=1则所有Channel都是相同的offset
不同的通道提取到的特征其实是不一样的,为提高网络的灵活性,可以适当调整group的个数,用dg表示Group数,则:
输入: B × dg ⋅ C dg × H × W B\times\text{dg}\cdot \frac{C}{\text{dg}}\times H\times W B×dg⋅dgC×H×W
卷积核: n × n × dg ⋅ C dg × 2 ⋅ n ⋅ n ⋅ dg n\times n\times\text{dg}\cdot \frac{C}{\text{dg}}\times 2\cdot n\cdot n\cdot \text{dg} n×n×dg⋅dgC×2⋅n⋅n⋅dg
输出: B × ( 2 ⋅ n ⋅ n ) ⋅ dg × H × W B\times (2\cdot n\cdot n)\cdot \text{dg}\times H\times W B×(2⋅n⋅n)⋅dg×H×W
Deformable RoI Pooling
思想和可变形卷积基本一样,ROI pooling之后的尺寸特征尺寸就固定下来了,所以用了一个FC连接
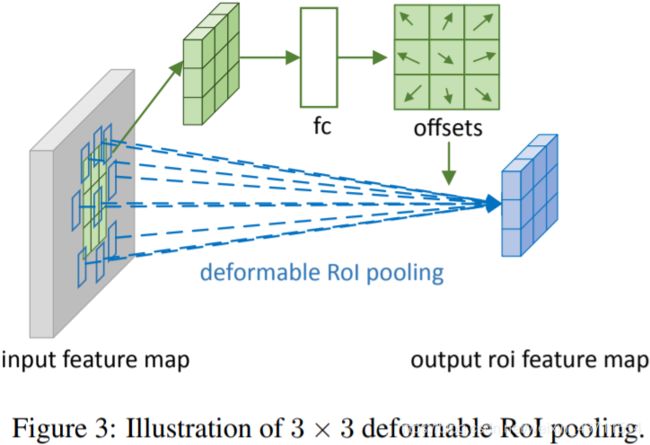
包括deformable position-sensitive(PS)RoI pooling,其思想与前面的基本一致,就是给一个可以学习的偏移量,然后再结合普通的position-sensitive(PS)RoI pooling

实验结果对比
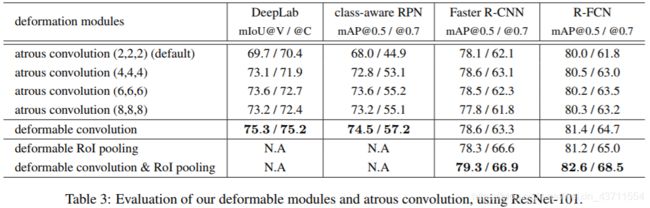
文中主网络将ResNet101 res5部分的 3 ∗ 3 3*3 3∗3卷积替换为可变形卷积(设置在靠后的卷积层,应该是为了从相对较为稳定的特征上学习偏移量),stride(原本为32)改为16,而dilated参数则设置为2以弥补减小stride带的感受野损失
下表中可看出:替换res5中3个卷积的时候效果最好。事实上v2中在 coco 数据集上的表现更好
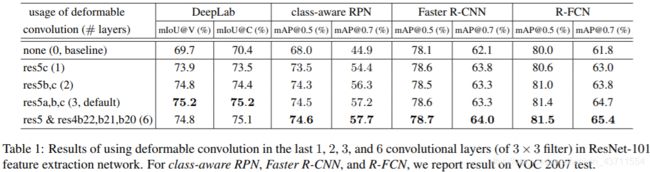
下表中可看出:deformable conv和 atrous conv 相比表现更好
可变形卷积Pytorch实现
双线性插值 【 8 】 ^{【8】} 【8】
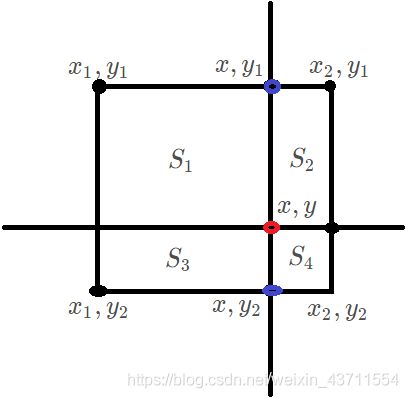
f ( x , y ) ≈ f ( x 1 , y 1 ) ( x 2 − x ) ( y 2 − y ) ⏟ S 4 + f ( x 2 , y 1 ) ( x − x 1 ) ( y 2 − y ) ⏟ S 3 + f ( x 1 , y 2 ) ( x 2 − x ) ( y − y 1 ) ⏟ S 2 + f ( x 2 , y 2 ) ( x − x 1 ) ( y − y 1 ) ⏟ S 1 \begin{aligned} {\color{red}f(x, y)} \approx{f\left(x_1,y_1\right)}\underbrace{\left(x_{2}-x\right)\left(y_{2}-y\right)}_{S_4} +{f\left(x_2,y_1\right)}\underbrace{\left(x-x_{1}\right)\left(y_{2}-y\right)}_{S_3} \\ +{f\left(x_1,y_2\right)}\underbrace{\left(x_{2}-x\right)\left(y-y_{1}\right)}_{S_2}+{f\left(x_2,y_2\right)}\underbrace{\left(x-x_{1}\right)\left(y-y_{1}\right)}_{S_1} \end{aligned} f(x,y)≈f(x1,y1)S4 (x2−x)(y2−y)+f(x2,y1)S3 (x−x1)(y2−y)+f(x1,y2)S2 (x2−x)(y−y1)+f(x2,y2)S1 (x−x1)(y−y1)
import torch
from torch import nn
class DeformConv2d(nn.Module):
def __init__(self, inc, outc, kernel_size=3, padding=1, stride=1, bias=None, modulation=False):
"""
Args:
modulation (bool, optional): If True, Modulated Defomable Convolution (Deformable ConvNets v2).
"""
super(DeformConv2d, self).__init__()
self.kernel_size = kernel_size
self.padding = padding
self.stride = stride
self.zero_padding = nn.ZeroPad2d(padding)
self.conv = nn.Conv2d(inc, outc, kernel_size=kernel_size, stride=kernel_size, bias=bias)
self.p_conv = nn.Conv2d(inc, 2*kernel_size*kernel_size, kernel_size=3, padding=1, stride=stride)
nn.init.constant_(self.p_conv.weight, 0)
self.p_conv.register_backward_hook(self._set_lr)
self.modulation = modulation
if modulation:
self.m_conv = nn.Conv2d(inc, kernel_size*kernel_size, kernel_size=3, padding=1, stride=stride)
nn.init.constant_(self.m_conv.weight, 0)
self.m_conv.register_backward_hook(self._set_lr)
@staticmethod
def _set_lr(module, grad_input, grad_output):
grad_input = (grad_input[i] * 0.1 for i in range(len(grad_input)))
grad_output = (grad_output[i] * 0.1 for i in range(len(grad_output)))
def forward(self, x):
offset = self.p_conv(x)
if self.modulation:
m = torch.sigmoid(self.m_conv(x))
dtype = offset.data.type()
ks = self.kernel_size
N = offset.size(1) // 2
if self.padding:
x = self.zero_padding(x)
# (b, 2N, h, w)
p = self._get_p(offset, dtype)
# (b, h, w, 2N)
p = p.contiguous().permute(0, 2, 3, 1)
q_lt = p.detach().floor()
q_rb = q_lt + 1
# 下标分别对应 lt:左上、rb:右下、lb:左下、rt:右上
q_lt = torch.cat([torch.clamp(q_lt[..., :N], 0, x.size(2)-1), torch.clamp(q_lt[..., N:], 0, x.size(3)-1)], dim=-1).long()
q_rb = torch.cat([torch.clamp(q_rb[..., :N], 0, x.size(2)-1), torch.clamp(q_rb[..., N:], 0, x.size(3)-1)], dim=-1).long()
q_lb = torch.cat([q_lt[..., :N], q_rb[..., N:]], dim=-1)
q_rt = torch.cat([q_rb[..., :N], q_lt[..., N:]], dim=-1)
# clip p
p = torch.cat([torch.clamp(p[..., :N], 0, x.size(2)-1), torch.clamp(p[..., N:], 0, x.size(3)-1)], dim=-1)
# bilinear kernel (b, h, w, N)
# 四个顶点对应的权重:lt:S4、rb:S1、lb:S2、rt:S3
g_lt = (1 + (q_lt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_lt[..., N:].type_as(p) - p[..., N:]))
g_rb = (1 - (q_rb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_rb[..., N:].type_as(p) - p[..., N:]))
g_lb = (1 + (q_lb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_lb[..., N:].type_as(p) - p[..., N:]))
g_rt = (1 - (q_rt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_rt[..., N:].type_as(p) - p[..., N:]))
# 获取周围四个点的值
# (b, c, h, w, N)
x_q_lt = self._get_x_q(x, q_lt, N)
x_q_rb = self._get_x_q(x, q_rb, N)
x_q_lb = self._get_x_q(x, q_lb, N)
x_q_rt = self._get_x_q(x, q_rt, N)
# 双线性插值
# (b, c, h, w, N)
x_offset = g_lt.unsqueeze(dim=1) * x_q_lt + \
g_rb.unsqueeze(dim=1) * x_q_rb + \
g_lb.unsqueeze(dim=1) * x_q_lb + \
g_rt.unsqueeze(dim=1) * x_q_rt
# modulation
if self.modulation:
m = m.contiguous().permute(0, 2, 3, 1)
m = m.unsqueeze(dim=1)
m = torch.cat([m for _ in range(x_offset.size(1))], dim=1)
x_offset *= m
x_offset = self._reshape_x_offset(x_offset, ks)
out = self.conv(x_offset)
return out
def _get_p_n(self, N, dtype):
p_n_x, p_n_y = torch.meshgrid(
torch.arange(-(self.kernel_size-1)//2, (self.kernel_size-1)//2+1),
torch.arange(-(self.kernel_size-1)//2, (self.kernel_size-1)//2+1))
# (2N, 1)
p_n = torch.cat([torch.flatten(p_n_x), torch.flatten(p_n_y)], 0)
p_n = p_n.view(1, 2*N, 1, 1).type(dtype)
return p_n
def _get_p_0(self, h, w, N, dtype):
p_0_x, p_0_y = torch.meshgrid(
torch.arange(1, h*self.stride+1, self.stride),
torch.arange(1, w*self.stride+1, self.stride))
p_0_x = torch.flatten(p_0_x).view(1, 1, h, w).repeat(1, N, 1, 1)
p_0_y = torch.flatten(p_0_y).view(1, 1, h, w).repeat(1, N, 1, 1)
p_0 = torch.cat([p_0_x, p_0_y], 1).type(dtype)
return p_0
def _get_p(self, offset, dtype):
N, h, w = offset.size(1)//2, offset.size(2), offset.size(3)
# (1, 2N, 1, 1)
p_n = self._get_p_n(N, dtype)
# (1, 2N, h, w)
p_0 = self._get_p_0(h, w, N, dtype)
p = p_0 + p_n + offset
return p
def _get_x_q(self, x, q, N):
b, h, w, _ = q.size()
padded_w = x.size(3)
c = x.size(1)
# (b, c, h*w)
x = x.contiguous().view(b, c, -1)
# (b, h, w, N)
# offset_x*w + offset_y
# 例如:a.shape=(30, 30),a[1][1]就是第 1*30+1 个元素
index = q[..., :N]*padded_w + q[..., N:]
# (b, c, h*w*N)
index = index.contiguous().unsqueeze(dim=1).expand(-1, c, -1, -1, -1).contiguous().view(b, c, -1)
x_offset = x.gather(dim=-1, index=index).contiguous().view(b, c, h, w, N)
return x_offset
@staticmethod
def _reshape_x_offset(x_offset, ks):
b, c, h, w, N = x_offset.size()
x_offset = torch.cat([x_offset[..., s:s+ks].contiguous().view(b, c, h, w*ks) for s in range(0, N, ks)], dim=-1)
x_offset = x_offset.contiguous().view(b, c, h*ks, w*ks)
return x_offset
参考代码二
补充
对conv,pooling操作深入探讨 【 6 】 ^{【6】} 【6】
附:im2col
可细分为四个阶段:
1. Indexing (im2col):本文关注的部分。
2. Computation (gemm):在im2col之后,conv就被转化为了一个dense matrix multiplication的问题。
本质上,conv还是一个线性模型就是因为在这一步还是一个线性变化。
有若干工作试图增强计算步骤的表示能力。从最开始的Network In Network到后来的Neural Decision Forest,
再到最近我们的Factorized Bilinear Layer,都是在这一步试图做出一些变化。
3. Reduce (sum):最简单的reduce操作就是求和,但是这个步骤还是有大量变化的余地。
例如,是否可以通过类似于attention一样的机制做加权求和?(这里defomble conv2已经做了)
是否可以通过random projection引入随机性?
5. Reindex (col2im):这步骤是第一步的逆操作。
参考文献
【1】可变形卷积网络(Deformable Convolutional Networks)
【2】Deformable Convolutional Networks
【3】STN-Spatial Transformer Networks-论文笔记
【4】详细解读Spatial Transformer Networks(STN)
【4】可变形卷积Deformable Convolution Net(DCN)理解
【5】Deformable ConvNets–Part5: TensorFlow实现Deformable ConvNets
【6】【VALSE 前沿技术选介17-02期】可形变的神经网络
【7】论文讨论&&思考《Deformable Convolutional Networks》
【8】双线性插值
【9】双线性插值的两种实现方法
【10】Deformable Convlolutional Networks算法笔记
【11】Review: DCN — Deformable Convolutional Networks, 2nd Runner Up in 2017 COCO Detection (Object Detection)