Large Margin Few-Shot Learning
Abstract
小样本学习的关键问题是学习泛化。本文提出了一个大边距原则,以提高基于度量的方法在小样本学习中的泛化能力。为了实现这一目标,我们开发了一个统一的框架,通过增加具有较大边距距离损失函数的分类损失函数来学习更具鉴别性的度量空间。在图神经网络和原型网络两种最先进的小样本学习方法上的大量实验表明,我们的方法可以大大提高现有模型的性能。
1 Introduction
小样本学习[4]是一个非常具有挑战性的问题,因为它旨在从很少的标记例子中学习。由于数据的稀缺性,传统的端到端监督模型,如从零开始训练深度学习模型[13,10]容易导致过拟合,而数据增强、正则化等技术无法解决这一问题。
解决小样本学习的一个成功视角是元学习。与需要大量标记集进行训练的传统监督学习不同,元学习通过从大量相似任务中提取知识然后转移知识以快速适应新任务来训练分类器,该分类器可以泛化到新任务。元学习已经探索了几个方向,包括学习微调[28,5,24,17],基于序列的方法[30,22],基于度量的学习[36,12]。
基于度量的小样本学习最近吸引了很多兴趣[36,32,6,34,8,21,12,29],可能是因为它的简单和有效性。基本思想是学习一个度量,它可以在度量空间中映射接近的相似样本和距离较远的不同样本(map similar samples close and dissimilar ones distant in the metric space ),这样查询就可以很容易地分类。各种基于度量的方法,如孪生网络[12]、匹配网络[36]、原型网络[32]和图神经网络[8],在度量的学习方式上有所不同。
基于度量的方法的成功依赖于学习到一个有判别性的度量空间。 然而,由于训练任务中的数据稀缺,很难学习到一个好的度量空间。 为了充分发挥基于度量的小样本学习的潜力,我们提出了一个大边距原则,用于学习更具辨别力的度量空间。 关键的观点是,来自不同类的样本应该在度量空间中尽可能地映射到不同的位置,以提高泛化并防止过拟合。在现有的基于度量的方法中,没有强制执行大边际约束。
为了填补这一空白,我们开发了一个统一的框架来施加大的边际约束。 特别是,我们用距离损失函数——三元组损失(the triplet loss) [31] 来增强度量学习方法的线性分类损失函数【线性分类?】,以训练更多度量空间(train a more metric space)。 我们的框架简单、健壮、非常容易实现,并且可以潜在地应用于许多采用线性分类器的度量学习方法。 两种最先进的度量学习方法——图神经网络 [8] 和原型网络 [32] 的应用表明,大边际约束可以显着提高原始模型的泛化能力,而计算开销很小。 除了三元组损失之外,我们还探索了其他损失函数来强制执行大边际约束。 所有的实验结果都证实了大边距原则的有效性。
虽然在机器学习的许多领域中已经广泛地研究了大边距方法,但本文还是第一次研究它在小样本学习(元学习)中的适用性和有用性。需要注意的是,这里所考虑的小样本学习问题与基于属性的小样本[16]或零镜头学习的设置有很大的不同[15,1,7,41]。
本文的贡献包括 1) 提出了一个大边缘原则来改进基于度量的小样本学习,2) 为大边缘小样本学习开发一个有效和高效的框架,以及 3) 进行广泛的实验来验证我们的建议。
2 Large Margin Few-Shot Learning
2.1 Few-Shot Learning
2.2 Large Margin Principle
How Few-Shot Learning Works. 为了从元训练中看不到的几个例子中快速学习,模型应该在元训练中获得一些可转移的知识。在基于度量的少镜头学习[12,8,32]中,其基本思想是学习一个非线性映射fφ(·),该映射可以模拟数据样本之间的类关系,即相似样本映射到度量空间的附近点,而不相似样本映射到距离较远的点。通常,映射fφ(·)将样本xi嵌入到一个相对低维的空间中,然后由线性分类器(如softmax分类器)对嵌入点fφ(xi)进行分类。注意,softmax分类器可以被认为是神经网络中最后一个完全连接的层。通过最小化交叉熵损失来学习映射fφ(·)和分类器参数:

其中wj是softmax分类器的权重矩阵W的第j列对应的分类器权重向量。 不失一般性,我们省略偏差 b 以简化分析。 注意 wj 可以被认为是嵌入空间中 j 类样本的类中心。
在学习了 fφ(·) 和 W 之后,模型就可以用于测试了。 图 2(a) 展示了一个 3-way 5-shot 测试用例,其中支持样本用点表示,查询样本用叉号表示。 同一类的样本用相同的颜色表示。 我们可以看到每个类的样本都映射到相应分类器权重向量 wj 周围的集群。 但是,属于第 1 类的查询样本可能会被错误地归入第 2 类,因为 w1 和 w2 之间的边距很小。
How Can It Work Better? 由于每个训练集包含的每个类的样本很少,样本均值的标准误差较高[23]。换句话说,类平均水平可能是对真实类中心的一个较差的估计,一些样本可能不能很好地代表自己的类。因此,该模型可能无法学习一个判别度量空间。
为了缓解这个问题并提高新类的模型泛化能力,我们建议在分类器权重向量(或类中心)之间强制执行较大的边距( margin )。 这个想法是来自不同类的样本应该在度量空间中映射得尽可能远。 如图 2(b)所示,通过扩大 w1 和 w2 之间的边距,可以正确分类查询样本。 值得注意的是,大边际原则使得分类器权重向量以平衡的方式分布(图2(b)),从而导致平衡的决策边界。
2.3 Model
为了强制执行大边距约束,我们建议为分类损失函数增加一个大边际损失函数,总损失由下式给出:
![]()
λ是一个平衡参数。我们选择三重损失 [31] 作为大边距函数,作用于度量空间中训练样本的嵌入:
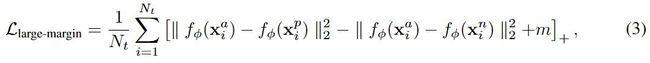

Nt是三元组的数量。可以选择训练集中的任何样本作为anchor。一旦选择,多个正样本和负样本与锚样本配对以形成多个三元组。
直观地说,增加三元损失有助于训练一个更具鉴别性的映射fφ(·),该映射在度量空间中嵌入同类样本的距离更近,嵌入不同类样本的距离更远。接下来,我们提供了一个理论分析,以说明三元损失如何重塑嵌入。
2.4 Analysis
我们通过研究 Llarge-margin 相对于 fφ(xi)(样本 xi 的嵌入)在反向传播期间的梯度,分析了增强的三元损失对嵌入的影响。
由于(3)中零损失项对梯度没有影响,我们只需要考虑方括号内损失为正的三元组,因此可以去除铰链操作(the hinge operation) [·]+。 要找到 Llarge-margin 相对于 fφ(xi) 的梯度,我们需要找到其中 xi 是锚样本、正样本或负样本的项。我们将样本划分为三个多重集。 第一组 Ss 包含与 xi 配对并与 xi 具有相同标签的所有样本。 第二组 Sd 包含与 xi 配对但与 xi 具有不同标签的所有样本。 第三组包含未与 xi 配对的样本。 这些多重集中一个元素的多重性是该元素与 xi 配对的三元组的数量。请注意,如果样本 xs ∈ Ss,则距离 ‖ fφ(xi) -fφ(xs) ‖22 被添加到损失中,而如果样本 xd ∈ Sd,则从损失中减去距离。 经过一些重排,(3)可以写成:
 其中 const 表示与 xi 无关的常数。 那么 Llarge-margin 相对于 fφ(xi) 的梯度可以求导为:
其中 const 表示与 xi 无关的常数。 那么 Llarge-margin 相对于 fφ(xi) 的梯度可以求导为:

其中 cs 是 Ss 中嵌入点集的中心,cd 是 Sd 中嵌入点集的中心。 通过(6),梯度由两部分组成。 第一部分是一个从 fφ(xi) 指向 Ss 中嵌入点中心的向量,它在训练期间将 fφ(xi) 拉到自己的类中,如图 2© 中的棕色箭头所示。 另一部分是从 Sd 中嵌入点的中心指向 fφ(xi) 的向量,使 fφ(xi) 远离其他类,如图 2© 中的红色箭头所示。 这表明增强的三元损失可以有效地强制执行大边际约束。
2.5 Discussion
When Does It Work? 三元损失的工作假设是嵌入点之间的相似性/不相似性可以通过欧几里德距离来衡量。 如果嵌入点位于度量空间中的非线性流形上,则欧氏距离无法反映它们的相似性。 这表明嵌入点在度量空间中应该是线性可分的,这表明三元损失应该与线性模型一起使用,例如度量空间中的 softmax 分类器。
Computational Overhead. 增加三元损失的计算开销在于两个方面:三元组选择和损失计算。 众所周知,当训练集很大时,三元组的在线选择可能非常耗时。 然而,在小样本学习中,每个类的样本数量在每次更新迭代中都是固定的,因此我们可以使用离线策略进行三元组选择。 事实上,我们只需要形成一次三元组,然后存储配对(the parings)并使用它们来索引每次更新中的嵌入。 这样,三元组选择的计算开销可以忽略不计。 对于损失计算,每次更新的时间复杂度为 O(Ntd),其中 Nt 是三元组的数量,d 是嵌入的维度。 因此,如果嵌入是低维的,则计算是有效的(有关运行时长的报告,请参阅第 3.3 节和第 4.3 节)。
4 Large Margin Prototypical Networks
在本节中,我们将提出的大裕度框架应用于流行的原型网络(PN) [32] for few-shot learning。PN易于实现,训练效率高,在一些基准数据集上取得了很好的性能
4.1 Prototypical Networks
PN 使用非参数 softmax 分类器。 即对于Qk中的一个查询样本xi,它被归入第k类的概率为:
 其中 d(·,·) 是衡量任意两个向量之间距离的度量,可以是余弦距离或欧几里得距离。 对于一个 episode 中的所有查询样本,分类损失为:
其中 d(·,·) 是衡量任意两个向量之间距离的度量,可以是余弦距离或欧几里得距离。 对于一个 episode 中的所有查询样本,分类损失为:
 如果d(·,·)为欧氏距离,PN实际上是嵌入空间[32]中的一个线性模型。因为:
如果d(·,·)为欧氏距离,PN实际上是嵌入空间[32]中的一个线性模型。因为: 其中wk = 2ck 和 bk =−cTk ck,公式(8)可以认为是一个线性分类器。
其中wk = 2ck 和 bk =−cTk ck,公式(8)可以认为是一个线性分类器。
4.2 Large Margin Prototypical Networks
PN 通过测量嵌入空间中查询和支持样本的类中心之间的距离来对查询和支持样本之间的类关系进行建模(PN models the class relationship between the query and support samples by measuring the distance between the query and the class centers of support samples in the embedding space)。 为了使 PN 更具辨别力,我们在其目标函数上增加了一个三元损失函数来训练一个大边缘原型网络(L-PN)。 三元损失函数在(3)中定义,其中 fφ(xi) 是输入样本 xi 通过 PN 的嵌入。
Triplet Selection. 原型网络的实现在更新迭代中不使用 mini-batch 。以5-shot 学习为例,在一次更新迭代中,对于每个类,一般的实践[32]是取样5个支持集样本和额外的15个查询集样本,因此每个类中的样本数量为20个。对于支持集和查询集中的每个样本(anchor),我们从anchor类中抽取10个正例; 对于每个正样本,我们从其他类中抽取 10 个负样本。 因此,对于每个样本,形成 100 个三元组。对于 5-way 5-shot 学习,Nc = 20 个类,总共形成 40,000 个(100 × 20 × 20)个三元组。 在我们在 Mini-Imagenet 上的实验中,形成三元组只需要 0.118 秒。 由于三元组的选择只需要在训练开始时进行一次,因此几乎不会产生计算开销。
4.3 Experimental Results
Results on Few-Shot Learning. 结果如表3所示。在 Omniglot数据集上,L-PN与PN性能相当。在 Mini-Imagenet 上,L-PN 在每个学习任务上都不断改进 PN。 对于具有欧几里德距离的 PN,1-shot 学习的改进比 5-shot 学习更显着,这是因为取同一类中多个支持样本的平均值有助于 PN 学习更具判别力的嵌入。
对于具有余弦距离的 PN,L-PN 大大提高了 PN。 最初,余弦 PN 的性能比欧几里得 PN 差得多。 纳入大边距损失函数极大地提升了其性能并使其与欧几里得 PN 相媲美甚至更好。 这表明大边距距离损失函数有助于余弦 PN 学习更好的嵌入空间,并可能缓解训练中的梯度消失问题。
Parameter Sensitivity.
我们还研究了 L-PN 中平衡参数 λ 和边距 m 的敏感性。 结果如图 5 所示。我们可以看到,对于 1-shot 学习,随着 λ 和 m 的变化,L-PN 始终优于 PN。 对于 5-shot 学习,当边距 m 从 5 变为 50 时,L-PN 优于 PN。当平衡参数 λ 大于 5 时,它仅比 PN 稍差。总的来说,结果表明 L-PN 是稳健的。
Running Time.
L-PN算法的计算开销非常小。对于Mini-Imagenet上的5-way 5-shot学习,L-PN的一次更新花费0.109s,而PN的0.105s,只产生3.8%的计算开销。
5 Related Works
5.1 Few-Shot Learning
早期关于少样本学习的工作主要集中在使用生成模型 [4] 和推理方法 [14]。 随着深度学习最近的成功,小样本学习已经用深度模型进行了大量研究,并取得了令人鼓舞的进展。 小样本学习的方法可以粗略地分为基于度量的方法、学习微调的方法和基于序列的方法。
Metric Based Methods 基于度量的方法的基本思想是学习一个度量来衡量样本之间的相似性 [36, 34]。 Koch等人[12] 提出了用于一样本学习的孪生神经网络。 它学习一个网络,该网络采用独特的结构来自然地对输入之间的相似性进行排序。 Mehrotra & Dukkipati [21] 提出使用残差块来提高 siamese 网络的表达能力。 它认为,拥有一个可学习且更具表现力的相似性目标是小样本学习的重要组成部分。 Bertinetto等人 [2] 提出在1-shot下通过构建第二个神经网络,该神经网络从单个样本中预测瞳孔网络(pupil network)的参数,来学习深度模型(瞳孔网络 pupil network)的参数。为了使这种方法可行,它提出了对瞳孔网络参数的若干因子分解(factorizations) 。Vinyals 等人 [36] 提出学习一个匹配网络,它通过使用循环神经网络将一个小的标记支持集和一个未标记的例子映射到它的标签。 该网络采用注意力和记忆机制(memory mechanisms)来实现快速学习,它基于一个原则:测试和训练条件必须匹配。 它提出了一种基于情节的训练程序,用于小样本学习,许多论文都遵循了该程序。 Snell 等人 [32] 提出了原型网络,通过计算每个类的原型表示的距离来进行小样本分类。 关键思想是原型是通过取同一类样本的嵌入向量的平均值来计算的。 Fort [6] 将其扩展到高斯原型网络。 Ren 等人 [29] 使用原型网络进行半监督的少样本学习。Kaiser 等人[11]提出通过在学习过程中不断更新记忆来实现小样本学习和终身学习。 它采用使用快速最近邻算法的大规模内存模块。 训练时无需重置记忆模块即可实现终身学习。 Garcia&Bruna [8] 提出了用于少样本分类的图神经网络。 它使用图结构对样本之间的关系进行建模,并且可以扩展到半监督的小样本学习和主动学习。Sung 等人[34] 认为嵌入空间应该由非线性分类器进行分类,并建议使用关系网络比较支持集和查询,其中距离标准是通过可训练的神经网络学习的,以测量两个样本之间的相似性。 我们的大边际方法可能适用于几乎所有这些模型。
Learning to Fine-Tune Methods. Munkhdalai & Yu [24] 提出了元网络,它可以跨任务学习元级知识,并可以通过快速参数化生成新模型。 Ravi & Larochelle [28] 通过学习初始条件和小样本学习的一般优化策略,提出了一种基于 LSTM 的元学习器模型,可用于在测试中更新学习器网络(分类器)。Finn 等人。 [5] 提出了一种与模型无关的元学习 (MAML) 方法,该方法可以学习模型的初始化,并且基于这种初始化,模型可以通过少量的梯度步骤快速适应新任务。 它可以结合到许多学习问题中,例如分类、回归和强化学习。 Li 等人。 [17] 提出了 Meta-SGD,它不仅学习初始化,而且学习随机梯度下降算法的更新方向和学习率。 实验表明,它可以比MAML更快更准确地学习。
Sequence Based Methods. 用于小样本学习的基于序列的方法积累了过去学到的知识,并能够利用学到的知识对新样本进行泛化。 Santoro 等人。 [30] 在循环神经网络上引入了外部存储器,以仅用几个样本进行预测。 通过外部存储器,它提供了快速编码和检索新信息的能力。 Mishra 等人。 [22] 提出了一种元学习器架构,它使用时间卷积和注意力机制来积累过去的信息。 它可以快速整合过去的经验,可以应用于小样本学习和强化学习。
5.2 Large Margin Learning
大间隔方法[26,35,40,43,25,42,31]在机器学习中得到了广泛的应用,包括多类分类[26]、多任务学习[25]、迁移学习[42]等。 对于大量关于大边距方法的文献,我们只回顾最相关的作品。 温伯格等人。 [40] 提出通过使用半定规划来学习用于 k 最近邻分类的马氏距离度量。 主要思想是 k 最近邻总是属于同一类,并且来自不同类的样本应该有很大的间隔。Parameswaran & Weinberger [25] 将大边距最近邻算法扩展到多任务范式。 施罗夫等人。 [31] 通过使用三元组损失来学习从人脸图像到紧凑(compact )欧几里得空间的映射,提出了一种用于人脸识别的大边距方法。Zien 和 Candela [43] 建议最大化 Jason-Shannon 散度以用于大边距非线性嵌入。 其思想是学习具有固定决策边界的数据的嵌入,这是与常见分类方法相反的过程。我们的方法在本质上类似于这种方法,在学习嵌入之前添加一个大的边距。 也有一些工作将大边缘方法应用于基于属性的零样本 [1] 和小样本学习 [16],但它们的问题设置与本文中考虑的小样本(元)学习有很大不同。
最近的一些工作 [27, 9, 33, 18, 19, 38, 39, 3, 20] 通过定义各种损失函数来实现大边距嵌入。 哈德塞尔等人。 [9]首先提出了对比损失(contrastive loss)并将其应用于降维。孙等人。 [33] 结合交叉熵损失和对比损失来学习深度人脸表示。 它通过结合识别任务和验证任务来减小intra-personal差异并扩大inter-persona的差异。刘等人。 [18] 提出了用于训练卷积神经网络的大边距 softmax 损失。 它通过定义一个可调整的和可乘的边距来明确地鼓励嵌入之间的类间可分离性和类内紧凑性。Liu 等人的动机是,学习到的特征应该具有判别性和聚合性。 [20]引入了同类(congenerous)余弦算法来优化数据之间的余弦相似度。 王等人。 [37]通过为每个类别引入一个向量并优化余弦相似度,提出了normface loss。 王等人。 [39] 通过在 L2 归一化嵌入和权重向量的余弦空间上定义附加边际,提出了 cosface 损失。邓等人。 [3] 通过在角度空间而不是余弦空间上设置附加边际,将 cosface 损失扩展到 arcface 损失。 所有这些损失函数都可以应用于实现小样本学习的大边距先验。 我们将在下一节中讨论和比较这些
6 Discussion
在本节中,我们实现并比较了前面提到的几个用于大边距小样本学习的损失函数,包括归一化三元损失、归一化contrastive损失[9,33]、normface损失[37]、cosface损失[39]和arcface损失[3]。我们在Mini-Imagenet上对这些模型进行了1 shot 和5 shot 学习的测试,结果汇总在表4、5、6、7中。
所有这些模型都考虑了 softmax 分类器的权重向量和嵌入的 L2 归一化:
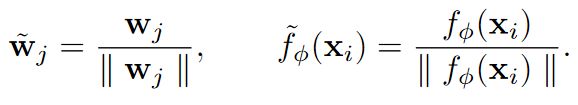 归一化后,第j个权重向量̃wj与嵌入向量̃fφ(xi)的夹角的余弦值为cos(θj,i) = ̃wTj ̃fφ(xi)。
归一化后,第j个权重向量̃wj与嵌入向量̃fφ(xi)的夹角的余弦值为cos(θj,i) = ̃wTj ̃fφ(xi)。
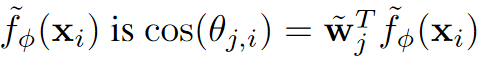
通过引入比例因子 s,softmax loss 可以改写为:
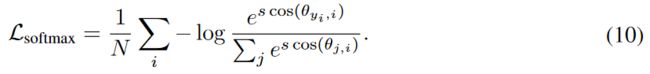

Normalized triplet loss. 同样,归一化的三元损失可以定义为:

其中 m 是边距,Nt 是三元组的数量。 归一化三元组损失(11)可以与(10)结合训练大边距图神经网络(GNN),总训练损失为:
![]() 类似地,它也可以结合到 softmax 损失中以训练大边距原型网络 (PN),归一化的嵌入通过因子 s 缩放。【只缩放嵌入?】
类似地,它也可以结合到 softmax 损失中以训练大边距原型网络 (PN),归一化的嵌入通过因子 s 缩放。【只缩放嵌入?】
我们在 Mini-Imagenet 上使用增加的归一化三元组损失测试 GNN 和 PN。 对于表 4 中的实验,我们设置边距 m = 0.5,它由 ‖fφ(xi) ‖2 下图 计算,即在训练开始时具有随机初始化参数的一个小批量中所有嵌入的 L2 范数的平均值 ,其中 Nb 是一个小批量中所有样本的数量。
 我们为所有实验设置 λ = 1,按照 Wang 等人的方法设置 s = 10。 [37]。 我们还测试了具有不同 m、λ 和 s 的归一化三元组损失,如表 6 所述。结果表明,归一化三元损失在所有学习任务中始终如一地改善了 PN 和 GNN,证明了大边距原则对小样本学习的益处。 对于 PN,归一化的三元损失比非归一化的三元损失表现更好。这表明在某些情况下,归一化嵌入空间有助于训练更好的分类器。 然而,对于 GNN,归一化的三元损失不如非归一化的三元损失稳健。 如表 5 和表 6 所示,后者始终优于前者。
我们为所有实验设置 λ = 1,按照 Wang 等人的方法设置 s = 10。 [37]。 我们还测试了具有不同 m、λ 和 s 的归一化三元组损失,如表 6 所述。结果表明,归一化三元损失在所有学习任务中始终如一地改善了 PN 和 GNN,证明了大边距原则对小样本学习的益处。 对于 PN,归一化的三元损失比非归一化的三元损失表现更好。这表明在某些情况下,归一化嵌入空间有助于训练更好的分类器。 然而,对于 GNN,归一化的三元损失不如非归一化的三元损失稳健。 如表 5 和表 6 所示,后者始终优于前者。

 Normalized contrastive loss 对比损失是由 Hadsell 等人 [9] 首先引入的并且被定义为:
Normalized contrastive loss 对比损失是由 Hadsell 等人 [9] 首先引入的并且被定义为:
 其中 m 是边距。 这个想法是将邻居拉在一起并将非邻居推开。 归一化对比损失可以通过替换嵌入(fφ(xi),fφ(xj))类似地定义使用归一化的 ( ̃fφ(xi), ̃fφ(xj))。 与归一化三元损失类似,归一化对比损失也可以结合softmax损失来训练大边距PN和大边距GNN。
其中 m 是边距。 这个想法是将邻居拉在一起并将非邻居推开。 归一化对比损失可以通过替换嵌入(fφ(xi),fφ(xj))类似地定义使用归一化的 ( ̃fφ(xi), ̃fφ(xj))。 与归一化三元损失类似,归一化对比损失也可以结合softmax损失来训练大边距PN和大边距GNN。
我们在 Mini-Imagenet 上使用增加的归一化对比损失测试 GNN。 我们可以看到,对于所有学习任务,归一化对比损失始终优于 GNN,这再次证实了大边距原则对于少样本学习很有用。结果总结在表 4 和表 6 中,其中参数设置与归一化三元损失相同。 我们可以从表 5 和 6 中看到,归一化对比损失与 5-shot 学习的非归一化三元损失相当,但对于更具挑战性的 1-shot 学习则不那么健壮。 我们还在实验中测试了非归一化对比损失,但发现它在训练中非常不稳定且容易发散。
Normface loss. 提出了normface loss [37]来提高人脸验证的性能。 它识别并研究了与 在 softmax 分类器的权重向量和嵌入上应用 L2 归一化 相关的问题。 Wang 等人 [37] 提出了四种不同的损失函数。这里我们使用 [37] 中报告的最佳模型。 normface 损失由两部分组成。 一个是softmax loss(10),另一部分是对比损失的另一种形式:
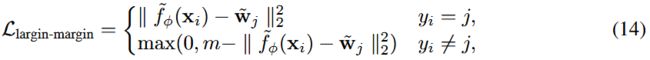 它是通过用 softmax 分类器的归一化权重向量 ̃wj 替换归一化对比损失中的 ̃fφ(xj) 获得的。 normface loss 也可以结合 softmax loss (10) 来训练大边界 GNN。 但是,它不能直接应用于 PN,因为 PN 使用非参数分类器。
它是通过用 softmax 分类器的归一化权重向量 ̃wj 替换归一化对比损失中的 ̃fφ(xj) 获得的。 normface loss 也可以结合 softmax loss (10) 来训练大边界 GNN。 但是,它不能直接应用于 PN,因为 PN 使用非参数分类器。
我们在 Mini-Imagenet 上使用增加的 normface 损失测试 GNN。 实验设置与归一化三元损失相同。 表 4、5 和 6 中的结果表明,对于所有学习任务,normface 损失明显优于 GNN,并且具有鲁棒性,可与未归一化的三元损失相媲美。 这表明对于使用参数分类器的基于度量的少样本学习方法来说,normface 损失也可能是实现大边际原则的一个很好的替代方案。
Cosface loss: Wang等人[39]提出cosface损失,定义为:

它在 L2 归一化嵌入和 softmax 分类器的权重向量的余弦空间中 引入了一个边距,这可以使学习到的特征更具辨别力。 cosface 损失可以用于训练大边距 GNN。 但是,它不能直接应用于 PN,因为 PN 使用非参数分类器。
我们在 Mini-Imagenet 上使用 cosface 损失函数测试 GNN。 对于表 4 中的实验,我们设置边距 m = 0.2。 我们还在表 7 中使用不同的 m 进行测试。对于所有实验,我们将 s = 10 正如在归一化的三元损失中的那样。 表 4 中的结果表明,当 m 选择恰当时,cosface loss 可以比 GNN 表现得更好,这再次表明了大边距原则的有用性。 然而,m 的选择并不重要。[39]建议,对于面部识别,正确选择M是0〜0.45。 然而,对于小样本学习,如表 7 所示,当 m 增加时,cosface loss 的性能显着下降。 这说明cosface loss对margin很敏感,整体上无法与非归一化的triplet loss相比。

Arcface loss. Deng等人[3]提出 arcface 损失,定义为:

arcface loss 通过在角度空间而不是余弦空间中定义边距 m 来扩展 cosface loss。 角边距比余弦边距具有更清晰的几何解释。 据[3]报道,与其他乘法角边距和附加余弦边距方法相比,cosface 损失可以获得更具辨别力的深度特征。 与cosface loss类似,可以应用于训练大间隔GNN,但不能直接应用于PN。
我们在 Mini-Imagenet 上使用 arcface 损失函数测试 GNN。 对于表 4 中的实验,我们设置边距 m = 0.1。 我们还使用[3] 所建议的不同的 m ∈ [0,0.5] 进行测试,见表 7 。对于所有实验,我们将 s = 10 正如归一化的三元损失中的那样。 结果表明,对于 5-shot 学习,arcface loss 可以比 m=0.1 的 GNN 表现更好,这再次证实了大边距原理的有效性。 然而,如表 7 所示,arcface 损失在大多数测试案例的训练中发散,并且仅在一种情况下收敛。 这表明 arcface loss 对 m 非常敏感,并且无法与用于少样本学习的非归一化三元损失相提并论。
总而言之,实验表明,所有大边距损失都可以显着改善原始的小样本学习模型,这证明了大边距原理的好处。 与其他损失函数相比,未归一化的三元损失有两个明显的优势。 首先, 它更通用,并且可以很容易地整合到基于度量的小样本学习方法中。 如上所述,normface loss、cosface loss 和 arcface loss 不能直接应用于使用非参数分类器的少样本学习方法。 其次,它比归一化三元损失、归一化对比损失、cosface 损失和弧面损失等其他损失函数更稳健。 在运行时,这些损失函数的计算开销都很小,类似于非归一化三元组损失的计算开销。
7 Conclusions
本文提出了基于度量的小样本学习的大边际原则,并证明了其在提高两种最先进方法【18年9月发表,这两种方法时PN和GNN】的泛化能力方面的有用性。 我们的框架简单、高效、健壮,可以应用于许多现有和未来的小样本学习方法。 未来的工作包括为大边距小样本学习开发理论保证,并将我们的方法应用于解决实际问题。