巴特沃斯、切比雪夫Ⅰ型、切比雪夫Ⅱ型和椭圆型滤波器的相同和不同之处

数字滤波器是由数字乘法器、加法器和延时单元组成的一种算法或装置。数字滤波器的功能是对输入离散信号的数字代码进行运算处理，以达到改变信号频谱的目的。

数字滤波器有多种分类方法，每一种方法都从不同的侧面揭示了数字滤波器的特性，主要有按频率分布特性的分类方法、按实现方式的分类方法和按脉冲响应特性的分类方法。

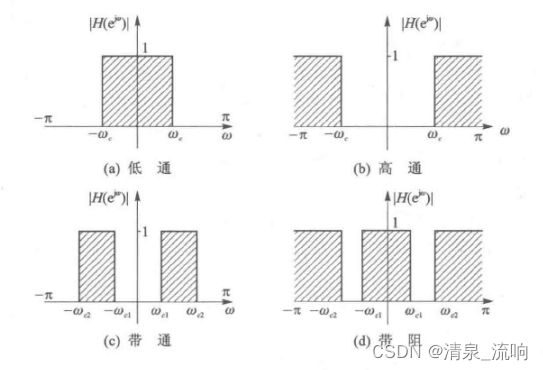
按频率分布特性分类方法与传统的模拟滤波器分类方法一致，将数字滤波器分为低通、高通、带通和带阻四类，如图下所示。

按数字滤波器对脉冲响应的特性来分类，数字滤波器可以分为有限脉冲响应FIR（Finite Impulse Response)数字滤波器和无限脉冲响应IIR(Infinite Impulse Response)数字滤波器。

FIR滤波器的传递函数只有零点，不含极点，它的单位脉冲响应h（k）只包含有限个非零值，即这种数字滤波器的脉冲响应是时间有限的。

IIR滤波器既有零点又有极点，它的脉冲响应h（k）中含有无限多个非零值，即这种滤波器的脉冲响应是无限长时间序列，在一定的时间后可能变小，但不会为零。

一般情况下，FIR滤波器比较适合用非递归型方式来实现，而IIR滤波器比较适合用递归型方式来实现。但无论是FIR滤波器还是IIR滤波器，都可用两种方法中的任一种来实现，只是按上述方法更简便而已。 

在信号处理过程中，所处理的信号往往混有噪声，从接收到的信号中消除或减弱噪声是信号传输和处理中十分重要的问题。根据有用信号和噪声的不同特性，提取有用信号的过程称为滤波，实现滤波功能的系统称为滤波器。在以往的模拟电路中用的都是模拟滤波器，在近代电信设备和各类控制系统中，由于数字化的普及，数字滤波器已得到了广泛的应用。

数字滤波器与传统模拟滤波器在实现方式上存在很大的差异。传统的模拟滤波器主要是硬件实现，它的硬件部分主要包括电容、电感和电阻等元件，而数字滤波器在硬件实现上主要涉及A/D转换器、D/A转换器、寄存器、存储器及微处理器等。数字滤波器的另一特点是可以用软件实现，即通过编程用算法来实现。数字滤波器与模拟滤波器相比，有其独特的优点，比如体积小、成本低、参数容易调整、有较高的精度、工作效率高等，但它们也有共同之处，例如滤波器的选频特性，即都用频率响应作为滤波器的主要技术指标。在设计数字滤波器时最常用的原型滤波器是巴特沃斯、切比雪夫Ⅰ型、切比雪夫Ⅱ型和椭圆型滤波器，下面通过案例介绍他们的不同之处。

案例、设计一个模拟带通滤波器,带通值为wp1=0.2π,wp2=0.3π,带阻值ws1=0.1π，ws2=0.4π，Rp=1，Rs=20。对这些指标分别以巴特沃斯、切比雪夫I型、切比雪夫Ⅱ型和椭圆型设计四类模拟滤波器。程序如下：

wp=[0.2*pi 0.3*pi];              % 设置通带频率
ws=[0.1*pi 0.4*pi];              % 设置阻带频率
Rp=1; Rs=20;                     % 设置波纹系数
% 巴特沃斯滤波器设计
[N,Wn]=buttord(wp,ws,Rp,Rs,'s'); % 求巴特沃斯滤波器阶数
fprintf('巴特沃斯滤波器 N=%4d\n',N) % 显示滤波器阶数
[bb,ab]=butter(N,Wn,'s');        % 求巴特沃斯滤波器系数
W=0:0.01:2;                      % 设置模拟频率
[Hb,wb]=freqs(bb,ab,W);          % 求巴特沃斯滤波器频率响应
plot(wb/pi,20*log10(abs(Hb)),'b')% 作图
hold on

% 切比雪夫I型滤波器设计
[N,Wn]=cheb1ord(wp,ws,Rp,Rs,'s');  % 求切比雪夫I型滤波器阶数
fprintf('切比雪夫I型滤波器 N=%4d\n',N) % 显示滤波器阶数
[bc1,ac1]=cheby1(N,Rp,Wn,'s');     % 求切比雪夫I型滤波器系数
[Hc1,wc1]=freqs(bc1,ac1,W);        % 求切比雪夫I型滤波器频率响应
plot(wc1/pi,20*log10(abs(Hc1)),'k')% 作图

% 切比雪夫II型滤波器设计 
[N,Wn]=cheb2ord(wp,ws,Rp,Rs,'s');  % 求切比雪夫II型滤波器阶数
fprintf('切比雪夫II型滤波器 N=%4d\n',N) % 显示滤波器阶数
[bc2,ac2]=cheby2(N,Rs,Wn,'s');    % 求切比雪夫II型滤波器系数
[Hc2,wc2]=freqs(bc2,ac2,W);       % 求切比雪夫II型滤波器频率响应
plot(wc2/pi,20*log10(abs(Hc2)),'r')% 作图

% 椭圆型滤波器设计
[N,Wn]=ellipord(wp,ws,Rp,Rs,'s');  % 求椭圆型滤波器阶数
fprintf('椭圆型滤波器 N=%4d\n',N) % 显示滤波器阶数
[be,ae]=ellip(N,Rp,Rs,Wn,'s');     % 求椭圆型滤波器系数
[He,we]=freqs(be,ae,W);            % 求椭圆型滤波器频率响应
% 作图
plot(we/pi,20*log10(abs(He)),'g')
axis([0 max(we/pi) -30 2]); %grid;
legend('巴特沃斯滤波器','切比雪夫I型滤波器','切比雪夫II型滤波器','椭圆型滤波器')
xlabel('角频率{\omega}/{\pi}'); ylabel('幅值/dB')
set(gcf,'color','w'); 

line([0 max(we/pi)],[-20 -20],'color','k','linestyle','--');
line([0 max(we/pi)],[-1 -1],'color','k','linestyle','--');
line([0.2 0.2],[-30 2],'color','k','linestyle','--');
line([0.3 0.3],[-30 2],'color','k','linestyle','--');

运行结果如下：

 

分析： 

①我们设计模拟滤波器的要求是：带通为wp1=0.2π，wp2=0.3π，带阻为ws1=0.1π，ws2=0.4π，Rp=1，Rs=20。在图中0.2和0.3（单位为pi)处画了两条竖虚线，可以看出这四类带通滤波器通带区间都在0.2～0.3之内。又在纵坐标-1dB和-20dB处画了两条横虚线，也可以看出通带内起伏在-1~0dB之间，阻带都小于或等于-20dB。这说明四类滤波器的幅频响应曲线形状虽不完全相同，但都满足了初始设计的要求。
②在运行程序时把每个滤波器的阶数都显示了出来，可以看到，在满足相同的设计要求的条件下，巴特沃斯滤波器用了4阶，阶数最多；切比雪夫I型滤波器和切比雪夫Ⅱ型滤波器用了3阶；椭圆型滤波器用了2阶，阶数最少。阶数少，相应的滤波器系数就少，在实现时就能减小运算量。
③从图3-2-5中可看出，巴特沃斯和切比雪夫Ⅱ型滤波器在通带是平坦的，切比雪夫I型和椭圆型滤波器在通带有波纹，而切比雪夫IⅡ型和椭圆型滤波器在阻带有波纹。
④从图3-2-5中还可看出，在满足相同的设计要求的条件下，切比雪夫Ⅱ型滤波器和椭圆型滤波器在过渡带内衰减更陡。

参考文献：MATLAB数字信号处理85个实用案例精讲——入门到进阶；宋知用（编著）