64.[GIS基础]矩阵、线性变换和仿射变换

转载请注明原始链接：http://blog.csdn.net/a464057216/article/details/54633312

后续此博客不再更新，欢迎大家搜索关注微信公众号“测开之美”，测试开发工程师技术修炼小站，持续学习持续进步。

矩阵

对角矩阵：所有非对角元素都为0的矩阵。对角矩阵的转置仍然是原对角矩阵。
单位矩阵：对角线元素都为1的对角矩阵。
矩阵乘法满足结合律，比如ABCDEF=(((((AB)C)D)E)F)=(AB)(CD)(EF)。所有括法都能计算出正确结果，但是有些括法标量乘法更少，寻找标量乘法最少的括法的问题称为矩阵链问题。

一般而言，方阵能描述任意线性变换。线性变换保留了直线和平行线，原点没有移动（线性变换不包含平移），但是其他几何性质如长度、角度、面积、体积可能会发生改变。从非技术角度来讲，线性变换可能“拉伸”某坐标系，但不会“弯曲”或“卷折”坐标系。

向量的每个坐标都表明了平行于相应坐标轴的有向位移，比如p、q、r定义为指向+x、+y、+z方向的单位向量，则任意向量v=xp+yq+zr，其中v=[x y z]。基向量不一定是三个坐标轴的方向，只要三个向量线性无关即可（不在同一平面），如果p、q、r是任意三个基向量，则可以以p、q、r为行建立一个3×3的矩阵：

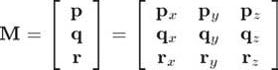
用一个向量乘以该矩阵，得到:

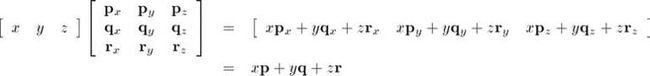
即如果把矩阵的行作为坐标系的基向量，那么乘以该矩阵就相当于进行了一次坐标转换。若有aM = b，称为矩阵M将向量a转到b。用矩阵A，B，C转换向量v，用行向量记法记作vABC，如果使用列向量，矩阵放在左边，转换从右向左发生，记作CBAv。阅读算法时一定要注意采用的是行向量还是列向量！

假设3维基向量是[1, 0, 0]，[0, 1, 0]和[0, 0, 1]，先看基向量乘以任意矩阵的情况：

即矩阵的每一行都能解释为转换后的基向量。

物体变换与坐标系变换

将物体变换一个量等价于将坐标系变换一个相反的量。当有多个变换时，需要以相反的顺序变换相反的量，例如物体顺时针旋转20度，扩大200%，等价于坐标系缩小200%，再逆时针旋转20度。实际使用中根据计算是否方便选择变换物体还是变换坐标系。

线性转换

旋转Rotation

2D旋转：假设绕原点旋转角度θ，逆时针旋转为正方向，顺时针旋转为负方向，则基向量p、q绕原点旋转得到基向量p^’、q^’得到的旋转矩阵为：

3D旋转：假设绕轴旋转角度为θ且轴穿过原点，在左手坐标系中采用左手法则规定旋转的正负向，在右手坐标系中采用右手法则规定旋转的正负向。
如果绕x轴旋转θ，旋转矩阵为：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RoLmL0GF-1587646284176)(https://img-blog.csdn.net/20170120193715009?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvYTQ2NDA1NzIxNg==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)]
如果绕y轴旋转θ，旋转矩阵为：

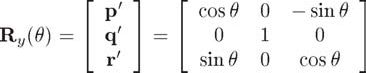
如果绕z轴旋转θ，旋转矩阵为：

如果绕任意轴旋转θ，该轴通过原点，用单位向量n描述旋转轴，旋转矩阵为：

缩放Scale

均匀缩放：沿原点在各方向应用同比例的缩放，物体的角度和比例不变。如果长度增加或减小因子k，面积增加或减小k²，体积增加或减小k³。
非均匀缩放：在各方向应用不同的比例因子缩放。
缩放因子设为k，|k|<1，物体变短，|k|>1，物体变长。k=0，是正交投影，k<0，是镜像，k>0是正常缩放。

2D缩放：假设分别沿x、y轴缩放k_x、k_y倍，则缩放矩阵为：

3D缩放：假设分别沿x、y、z轴缩放k_x、k_y、k_z倍，则缩放矩阵为：

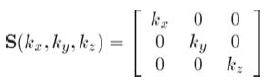
2D坐标系中，基向量沿任意单位向量n的方向缩放，k为缩放因子，缩放矩阵为：

3D坐标系中，基向量沿任意单位向量n的方向缩放，k为缩放因子，缩放矩阵为：

正交投影Orthographic Projection

在某个方向上用0做缩放因子，称为正交投影，或平行投影（原来的点到投影点的直线互相平行）。
投影一般用于降维，如将3D点复制给2D点，抛弃z分量，只复制x和y分量。
向某个轴投影，是对与该轴垂直的方向使用缩放因子0进行缩放的过程。
向某个平面投影，是对与该平面垂直的方向使用缩放因子0进行缩放的过程。

2D向x轴投影的投影矩阵：

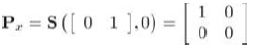
2D向y轴投影的投影矩阵：

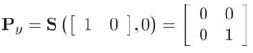
3D向xy平面投影的投影矩阵：

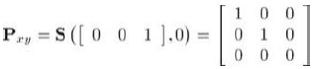
3D向xz平面投影的投影矩阵：

3D向yz平面投影的投影矩阵：

2D向任意直线投影的投影矩阵（其中单位向量n与投影直线垂直）：

3D向任意平面投影的投影矩阵（其中单位向量n与投影平面垂直）：

##镜像/反射Mirroring/Reflection
镜像相当于某个方向的缩放因子为-1。
2D中沿通过原点且垂直于单位向量n的反射轴的镜像变换矩阵：

3D中沿通过原点且垂直于单位向量n的反射平面的镜像变换矩阵：

PS：物体沿不同的轴或平面镜像两次以后的效果，通过旋转物体也能实现。

切变 Shearing

切变是扭曲变换，会变化物体的角度，但是面积和体积保持不变。
2D中切变的基本思想是将某一个坐标的乘积加到另一个坐标上，比如x^’=x+sy：

2D中x坐标根据坐标y被切变的切变矩阵为（s控制切变方向和量）：

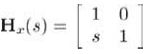
2D中y坐标根据坐标x被切变的切变矩阵为（s控制切变方向和量）：

3D中切变的基本思想是取一个坐标乘以不同的因子分别加到其他两个坐标上。
3D中x、y坐标根据坐标z被切变的切变矩阵为（s、t控制切变方向和量）：

3D中y、z坐标根据坐标x被切变的切变矩阵为（s、t控制切变方向和量）：

3D中x、z坐标根据坐标y被切变的切变矩阵为（s、t控制切变方向和量）：

注意区分非均匀缩放和切变。

线性变换（Linear Transformation）与仿射变换（Affine Transformation）

如果映射F(a)满足F(a+b)=F(a)+F(b)以及F(ka)=kF(a)，则F是线性映射。旋转、缩放、正交投影、镜像、切变都是线性变换。线性变换可能造成“拉伸”，但是直线不会“弯折”（即使是切变也是如此）。

仿射变换在线性变换的基础上增加了平移，任何具有形式v^’=vM+b的变换都是仿射变换。仿射变换是线性变换的超集。

如果觉得我的文章对您有帮助，欢迎关注我(CSDN:Mars Loo的博客)或者为这篇文章点赞，谢谢!