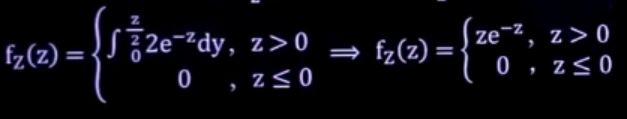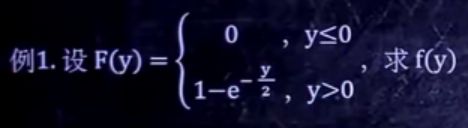【概率论与数理统计】猴博士 笔记 p17-20 一、二维连续型：已知F,求f；已知f,求f

一维连续型已知F，求f

题型：

步骤：f是F的导数，对F求导即可得到f。

例1：

解：

例2：

解：

一维连续型已知f，求f

题型：已知f(x)，求f(y)

步骤：（注意，要满足要求：Y=g(X)满足单增或单减才能用公式法）

看起来有点抽象，我们看一道例题：

此题中Y=g(X)是Y=2X，是单增的，所以可以用公式法。

第一步：通过Y=g(X)得出X=h(Y):
$$X=\frac{Y}{2}$$
第二步：用h(Y)替换f(x)各式子中的x。
$$\begin{gathered} 原式为f_X(x)=\{\begin{array}{l}0,x\le 0\\ e^{-x},x>0\end{array} \\ X=\frac{Y}{2}替换后 \\ {f}_X(x)=\{\begin{array}{l}0,y\le 0\\ e^{-\frac{y}{2}},y>0\end{array} \end{gathered}$$
第三步：在f(x)各式子的末尾后乘上|h’(y)|
$$f_X(x)=\{\begin{array}{l}0\ast |(\frac{y}{2}{)}^{\prime }|,y\le 0\\ e^{-\frac{y}{2}}\ast |(\frac{y}{2}{)}^{\prime }|,y>0\end{array}$$
第四步：将f(x)变成f(y)
$$f_X(x)=\{\begin{array}{l}0,y\le 0\\ \frac{1}{2}{e}^{-\frac{y}{2}},y>0\end{array}$$
答案：

二维连续型已知F，求f

步骤：求偏导

例题1：

解：

求偏导：
如果一个（对x、y）求偏导的式子并不是既有x又有y，那么它的偏导就是0.
如果既有x又有y，那么正常求即可。

因此答案：

二维连续型已知f，求f

步骤：有三种求法：普通求法、公式法(消x、消y)
看一道例题：

我们以公式法（消y）来举例子：

第一步：
$$Z=X+2Y=>Y=\frac{Z-X}{2}=>y=\frac{z-x}{2}$$

第二步：
$$\begin{gathered} 原式为f(x,y)=\{\begin{array}{l}2e^{-(x+2y)},x>0,y>0\\ 0,其他\end{array} \\ 替换后 \\ f(x,y)=\{\begin{array}{l}2e^{-(x+2\ast (\frac{z-x}{2}))}\ast |\frac{\partial \frac{z-x}{2}}{\partial z}|,x>0,\frac{z-x}{2}>0\\ 0,其他\end{array} \\ 化简后f(x,y)=\{\begin{array}{l}{e}^{-z},x>0,\frac{z-x}{2}>0\\ 0,其他\end{array} \end{gathered}$$
第三步：
$$\begin{gathered} f(x,y)=\{\begin{array}{l}{e}^{-z},x>0,x<z\\ 0,其他\end{array} \\ f(x,y)非0式子里的范围:x<z,x>0 \\ 范围存在时,z>0 \\ 范围不存在时,z\le 0 \\ 范围存在是x的范围是(0,z) \end{gathered}$$
第四步：
$$f_Z(z)=\{\begin{array}{l}{\int }_0^z{e}^{-z}dx,z>0\\ 0,z\le 0\end{array}=>f_Z(z)=\{\begin{array}{l}z{e}^{-z},z>0\\ 0,z\le 0\end{array}$$

用上述方法尝试消去x，能得到答案：