matlab方差分析加代码和结果分析

方差分析用于两个及两个以上样本均数差别的显著性检验，用于定类数据和定量数据的差异分析，例如温度对植物生长高度的影响，或者年龄对智商大小的影响等。方差分析分为单因素方差分析、不考虑交互作用的双因素方差分析和考虑交互作用的双因素方差分析三类。

方差分析的前提：

1.正态分布性：即样本数据符合正态分布或来自正太分布样本总体

2.方差齐性：对于不同水平的正态分布总体的方差相等

3.独立性：不同总体抽取的样本相互独立

单因素方差分析：

（1）单因素方差分析是用来研究一个控制变量的不同水平是否对观测变量产生了显著影响。这里，研究单个因素对观测变量的影响，所以称为单因素方差分析。matlab中单因素方差分析通过函数anova1函数实现。

调用格式：

p=anova1(y)

p=anova1(y,group)%group用于不均匀样本进行分组，见例题2

p=anova1(y,group,displayopt)%当displayopt为'on'(默认)时，启用ANOVA表和箱线图显示;当displayopt为'off'时，抑制显示。

[p,tbl]=anova1(---)%返回单元格数组tbl中的ANOVA表(包括列和行标签)，使用前面语法中的任何输入参数组合。

[p,tbl,stats]=anova1(---)%显示箱式图

例题1.通过单因素方差分析温度对反应速率的影响是否显著

matlab程序如下：

x=[0.4 0.6 1.1  6.0 21.1 
  0.5 1.1 3.0  9.6 33.5
  2.8 7.5 12.6 27.0 63.2
  2.8 4.4 6.2  16.2 45.1];
[p,tbl,stast]=anova1(x);

结果显示：

 由F=11.8，p>F的值0.0002<0.05，故F的值落在拒绝域内，于是接受假设，认为4个水平的均值不全相等，即温度不同对反应速率的影响是极其显著的。

（2）不均匀样本的输入，和上述基本一致，只是多了一个分组。

例题2：实验三种不同的饲料对鸡的重量影响，下表为9只鸡的增重。

 代码如下：

x=[51,40,43,48,23,25,26,23,28];
g=[1 1 1 1,2 2 2,3 3];%分组
% % 分组还可以用下述方法写入
% g=[ones(1,4),2*ones(1,3),3*ones(1,2)];
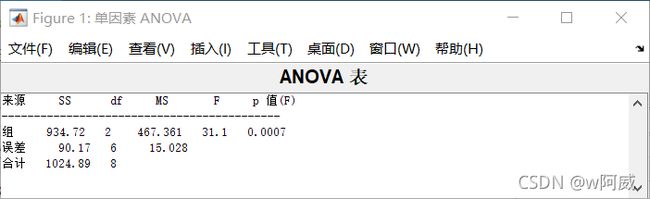
[p,tbl,stast]=anova1(x,g);

结果：

 由F=31.1，P>F的值0.007<0.05，故F的值落在拒绝域内，于是接受假设，认为3个水平的均值不全相等，即不同的饲料对鸡增重的影响显著。

不考虑交互作用的双因素方差分析

通过实验设计，在实验中安排两个因素有所变化，取不同的的状态水平，而其它因素都在设计的状态下保持不变的实验叫做双因素实验。假设因素A与因素B不同水平总体均值相等。

调用格式：

p=anova2(y,reps)%返回平衡的双向方差分析的p值，用于比较y中两列或多列的观察值和两行或多行的均值。Reps是每个因子组组合的重复次数，必须是常数，表明设计是平衡的。对于不平衡设计，请使用anovan。方差分析anova2函数测试列和行因素及其相互作用的主要影响。要测试相互作用效果，reps必须大于1。

p=anova2(y,reps,displayopt)

[p,tbl]=anova2(---)

[p,tbl,stats]=anova2(---)

例题：4种不同的肥料对5种不同品种的玉米增长量的测试值见下表

                 

代码如下：

x=[ 2.4	2.5	3.2	3.4	2.0
    2.6	2.2	3.2	3.5	1.8
    2.1	2.7	3.5	3.8	1.8
    2.4	2.7	3.1	3.2	2.3];
[p,tbl,stast]=anova2(x);

 结果分析：

 对于因素A，由F=0.23，p>F的值0.8747大于0.05，故认为不同的饲料种类玉米生长的影响显著性较低。对于因素B，由F=26.79，p>F的值为0，认为很小很小，远远小于0.05，故认定不同的玉米种类对玉米增长量的影响极其显著。

考虑交互作用的双因素方差分析：

这里有3个不同的因素，即因素A，因素B，以及因素A和因素B交互在一起的作用，所以假设A 因素各水平总体均值相等，B 因素各水平总体均值相等，AB 因素各水平总体均值相等。

例题：不同鱼料对小鱼增重的数据测试如下表：

 代码：

x=[7,10;15,12
    11,14;13,15
    18,21
    12,19];
[p,tbl,stast]=anova2(x,3);

结果分析：

对于鱼料A，由F=1.89，p>F的值为0.2064>0.05,故认为不同鱼料A对小鱼增重的影响是不显著的。

对于鱼料B，由F=7.07，p>F的值为0.0289<0.05，故认为不同的鱼料B对小鱼的增种影响显著，对于鱼料A和鱼料B交互在一起的新的因素，由F=0.68，p>F的值0.4333>0.05,故认为鱼料A和鱼料B交互在一起对小于增重的影响是不显著的。