矩阵的坐标系变换

---

矩阵的坐标系变换

一、矩阵

一个$m\times n$的矩阵可以将一个$n$维的向量转化成一个$m$维度的新向量，例如rotation matrix
$$\left[\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]\cdot \left[\begin{array}{c}1\\ 0\end{array}\right]=\left[\begin{array}{c}cos\theta \\ sin\theta \end{array}\right]$$
我们可以将上式理解为rotation matrix将向量$e_1$旋转了一个角度$\theta$， 得到了一个新的向量。

二、坐标系变换

我们也可以将上式理解为矩阵对坐标系的变换。对比于将一个向量转化成了一个新的向量，在向量变换的过程中，我们认为坐标系是没有改变的。我们始终是以$(e_1,e_2)$作为basis。但当我们将矩阵变换理解为坐标系变换的时候，我们的初始坐标系并不是$(e_1,e_2)$，而是以$(cos\theta ,sin\theta ),(-sin\theta ,cos\theta )$作为basis的坐标系（虚线坐标系）。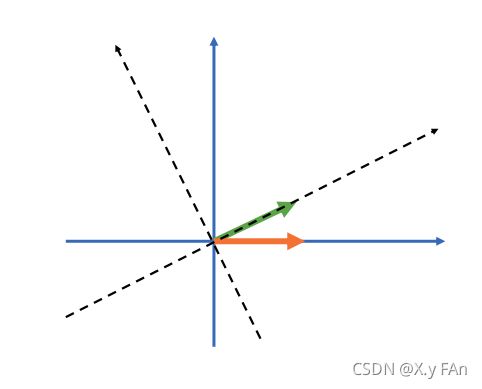
在这个虚线坐标系下，绿色向量的坐标为$(1,0)$。而矩阵变换告诉了我们这个向量在$(e_1,e_2)$为basis的坐标系（蓝色坐标系）下的坐标，也就是矩阵变换的结果$(cos\theta ,sin\theta )$。我们还可以发现，这个矩阵体现了如何用$(e_1,e_2)$的线性组合表示虚线坐标系。这个矩阵可以理解为，要想用$(e_1,e_2)$表示虚线坐标系，虚线坐标系第一个eigenvector是$cos\theta e_1+sin\theta e_2$，虚线坐标系的第二个eigenvector是$-sin\theta e_1+cos\theta e_2$。而矩阵的值，正是线性组合的系数。

蓝色坐标系为我们的目标坐标系（结果$(cos\theta ,sin\theta )$的坐标系），虚线坐标系为我们的起始坐标系$(1,0)$的坐标系，矩阵则是以目标坐标系表示起始坐标系的系数。矩阵的变换就是已知向量在起始坐标系下的坐标，求向量在目标坐标系下的坐标。

再举一个目标坐标系不是$(e_1,e_2)$的例子，假如我们的目标坐标系为：
$$\left[\begin{array}{cc}1& 2\\ 2& 0\end{array}\right]$$
起始坐标系为$(e_1,e_2)$， 我们想知道在目标坐标系下向量$(3,2)$的坐标是多少。那么我们的矩阵就是目标坐标系来表示起始坐标系的系数。
$$e_1=0\ast (1，2)+\frac{1}{2}\ast (2,0)$$
$$e_2=\frac{1}{2}\ast (1，2)+-\frac{1}{4}\ast (2,0)$$
所以，矩阵为：
$$\left[\begin{array}{cc}0& 1/2\\ 1/2& -1/4\end{array}\right]\cdot \left[\begin{array}{c}3\\ 2\end{array}\right]=\left[\begin{array}{c}1\\ 1\end{array}\right]$$
也就是在目标矩阵下，向量（3， 2）的坐标是（1， 1）