KMP算法总结
一、KMP算法介绍
KMP(Knuth、Morris、Pratt三人设计的算法);
KMP算法主要用于模式匹配,简单地说就是字符串的匹配,比如A="abc",B="b",问:B是否是A的子串,此时就需要用到KMP算法;因为普通的算法效率太低;
而KMP可以做到O(m+n)的线性时间;
二、普通模式匹配算法
模式匹配算法简单地说就是给定两个字符串A、B,看是否B是A的子串,Java 中String类的indexOf()就是实现这个功能;
普通模式匹配算法思想:
比如有两个字符串A:"ababc",B:"abc";
第一步:初始化 i=1,j=1;(A[0]与B[0]可以空着或者存放字符串的长度);
第二步:循环遍历A和B,如果A[i]==B[j],则i++,j++;
第三步:当跳出循环时,判断是否B是A的子串;
步骤:
1. i = 1,j=1;
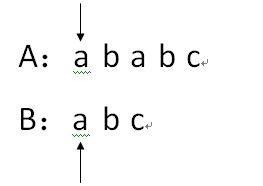
2.因为A[i]==B[j],因此i++,j++;
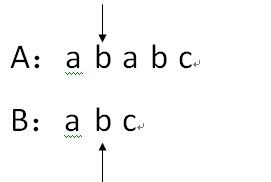
3.因为A[i]==B[j],因此i++,j++;
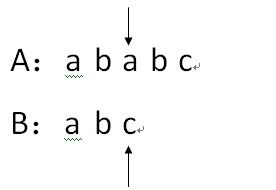
4.因为A[i]!=B[j],所以 j还原为1,i还原为 i-j+2;
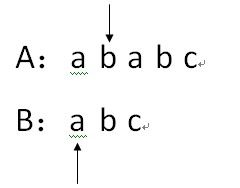
5.因为A[i]!=B[j],所以 j还原为1,i还原为 i-j+2;

6.因为A[i]==B[j],因此i++,j++;
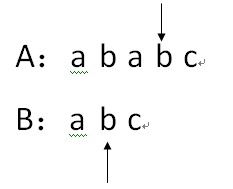
7.因为A[i]==B[j],因此i++,j++;

8.因为A[i]==B[j],因此i++,j++;
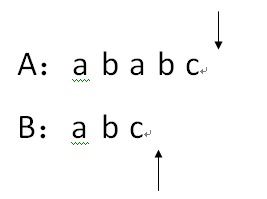
9.因为i和j同时越界,说明在最后匹配,所以B是A的子串;
从上面的步骤中可以看出:
普通的模式匹配算法是效率低下的,有许多步骤都是冗余的,比如第5步:A[2]和B[1]的比较,因为在之前,我们已经比较过:A[2]=B[2],B[1]!=B[2],所以A[2]!=B[1],因此这步就是多余的。
算法如下:
private static int indexOf(String a, String b) {
//1.定义两个指针,分别指向a和b
int i = 0;
int j = 0;
//2.遍历
while(i<a.length()&&j<b.length()){
if(a.charAt(i)==b.charAt(j)){
i++;
j++;
}
else{
i = i-(j-1);
j = 0;
}
}
/*
* 匹配
* 1.匹配a的中间字符串i<a.length()
* 2.匹配a的最后字符串(i==a.length()&&j==b.length())
* */
if((i==a.length()&&j==b.length())||i<a.length()){
return i-b.length();
}
else{
return -1;
}
}
三、KMP算法
KMP算法主要思想:i不用回朔,只需要不断递增即可,只需要j回朔即可;
回朔j的规则:
(1)将前面的已经匹配的字符串取出来,找出一个子串,使得此子串既为匹配的字符串的最长前缀也是最长后缀;比如:
匹配的字符串为"ababa",可以看出,"a"、“aba”既是前缀也是后缀,但是“aba”长度较长,所以 j'=“aba".length();
用数学语言表达就是:
当A[i-j+1...i]=B[1...j]且A[i+1]!=B[j+1],则需要调整j,使得重新A[i-j+1....i]=B[1...j];
而我们又将回朔j的这个过程用一个数组进行预先计算,记作p[],p[j]表示当有j个字符串已经匹配,但是第j+1个字符不匹配时回朔后的j'的新值;
比如前面的例子p[5]=3;因为"ababa"的长度为5,回朔后的j=3;
比如如下例子:
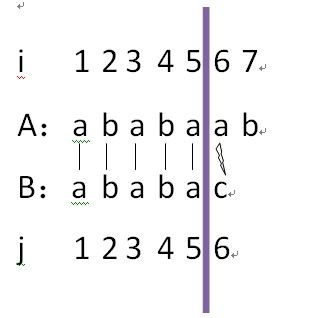
A[1...5]=B[1...5],A[6]!=B[6],i=6,j=5,因此我们需要回朔j(根据预先算好的p[]数组,回朔就是 j=p[j]);
回朔原理:公共的部分为“ababa”,我们可以从此字符串中看出:"aba"是最长的前缀和后缀,因此我们可以进行如下图的变换,使得j=3;
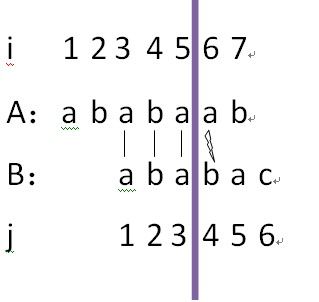
A[3...5]=B[1...3],但是A[6]!=B[4],i=6,j=3,因此继续回朔,使得j=1;如下图所示
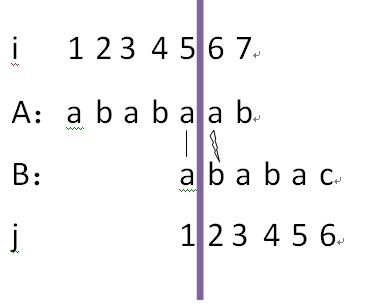
A[5]=B[1],但是A[6]!=B[2],i=6,j=1,所以继续回朔,如下图所示,使得j=0:
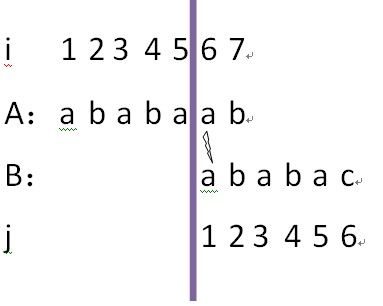
因为j=0,所以不能继续回朔,又因为i索引到了A字符串的尾端,但是j仍然不是B的尾端,因此说明B不是A的子串;
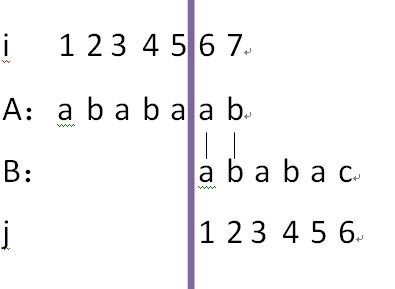
KMP算法如下:
/**
* O(m+n) 平摊分析
*
* @param a 表示文本字符串
* @param b 表示模式字符串
* @return
*/
public static int KMP_indexOf(String a,String b){
int n = a.length();
int m = b.length();
//变成字符数组的原因是因为我们需要从索引1开始记录数据,比如a = "aba",则cha = {' ','a','b','a'};
char cha[] = (" "+a).toCharArray();
char chb[] = (" "+b).toCharArray();
int j = 0; //b的指针
int[] p = computePArray(chb); //根据b字符串预先计算出p数组
for(int i=1;i<=n;i++){
while(j>0 && chb[j+1]!=cha[i]){ //j值最多只能减少m次,通过把m次摊还给n次for循环
j = p[j]; //回朔
}
if(chb[j+1]==cha[i]){
j++;
}
if(j==m){ //j已经匹配到了尾端,所以全部匹配
return i-m;
}
}
return -1;
}
private static int[] computePArray(char[] chb) {
int[]p = new int[chb.length+1];
p[1] = 0;
int j = 0;
for(int i=2;i<chb.length;i++){
while(j>0&&chb[j+1]!=chb[i]){
j = p[j];
}
if(chb[j+1]==chb[i]){
j++;
}
p[i] = j;
}
return p;
}
预先计算p数组的规则:
举个例子,比如B=“ababac”,
1.初始化p[],并且将p[1]=0 ,i=2,j=0;
2.因为B[2]!=B[1],所以p[2]=0,i=3,j=0;p[2]=0;
3.因为B[3]=B[1],所以 j++,即j=1,i=4;p[3]=1;
4.因为B[4]=B[2],所以j++,即j=2,i=5;p[4]=2;
5.因为B[5]=B[3],所以j++,即j=3,i=6,p[5]=3;
6.因为j>0,并且B[6]!=B[4],所以j=p[j]=2;
7.因为j>0,且B[6]!=B[2],所以j=p[j]=0;
8.因为j=0,并且B[6]!=B[2],所以p[6]=0;
参考文献:
http://www.matrix67.com/blog/archives/115/ 这篇文章写的很不错;
此文的实现方法也很好:
public static void computePArray(String T,int p[]){
T = " "+T;
int j=0;
p[1] = 0;
for(int i=2;i<p.length;i++){
while(j>0&&T.charAt(j+1)!=T.charAt(i)){
j = p[j];
}
if(T.charAt(j+1)==T.charAt(i)){
j++;
}
p[i] = j;
}
}