博弈最高位POJ 1704(Georgia and Bob-Nim博弈)
新手发帖,很多方面都是刚入门,有错误的地方请大家见谅,欢迎批评指正
|
Georgia and Bob
Description
Georgia and Bob decide to play a self-invented game. They draw a row of grids on paper, number the grids from left to right by 1, 2, 3, ..., and place N chessmen on different grids, as shown in the following figure for example:
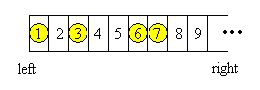
Georgia and Bob move the chessmen in turn. Every time a player will choose a chessman, and move it to the left without going over any other chessmen or across the left edge. The player can freely choose number of steps the chessman moves, with the constraint that the chessman must be moved at least ONE step and one grid can at most contains ONE single chessman. The player who cannot make a move loses the game. Georgia always plays first since "Lady first". Suppose that Georgia and Bob both do their best in the game, i.e., if one of them knows a way to win the game, he or she will be able to carry it out. Given the initial positions of the n chessmen, can you predict who will finally win the game? Input
The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case contains two lines. The first line consists of one integer N (1 <= N <= 1000), indicating the number of chessmen. The second line contains N different integers P1, P2 ... Pn (1 <= Pi <= 10000), which are the initial positions of the n chessmen.
Output
For each test case, prints a single line, "Georgia will win", if Georgia will win the game; "Bob will win", if Bob will win the game; otherwise 'Not sure'.
Sample Input 2 3 1 2 3 8 1 5 6 7 9 12 14 17 Sample Output Bob will win Georgia will win Source |
先将数一一配对(a,b),若是奇数则把最左边与0配对。
那么若对方向左挪a,我们也挪动b雷同步数。
那么唯一会影响的就是各配对间的间隔。
假设有间隔c1,c2..cn
那么相当于每次选一个数,减去最少1.
这就像nim取石,有n堆石子,每次最少取走其中一堆的最少一个,谁最早没石子取就输。
这个问题的答案是 c1^c2^..^cn=0时有必输解,否则必胜。
都懂得……
证明:
假设你面临一个c1^c2^...^cn=0的局势
A:取走多少石子使c1^c2^...^cn=k
B:取走ci的最高位与k的最高位雷同的那堆 ci^k个 //最高位的1^1=0,所以ci^k<ci
A:恭喜你还是必输
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<functional>
#include<iostream>
#include<cmath>
#include<cctype>
#include<ctime>
using namespace std;
#define For(i,n) for(int i=1;i<=n;i++)
#define Fork(i,k,n) for(int i=k;i<=n;i++)
#define Rep(i,n) for(int i=0;i<n;i++)
#define ForD(i,n) for(int i=n;i;i--)
#define RepD(i,n) for(int i=n;i>=0;i--)
#define Forp(x) for(int p=pre[x];p;p=next[p])
int T,n,a[100000+10];
int main()
{
scanf("%d",&T);
while (T--)
{
scanf("%d",&n);
For(i,n) scanf("%d",&a[i]);
sort(a+1,a+1+n);
int tmp=0,head=1;
if (n%2) tmp=a[1]-1,head++;
for(int i=head;i<=n;i+=2)
{
tmp^=(a[i+1]-a[i]-1);
}
if (tmp) puts("Georgia will win");
else puts("Bob will win");
}
return 0;
}
文章结束给大家分享下程序员的一些笑话语录: 不会,Intel会维持高利润,也会维持竞争局面,国外的竞争不是打死对方的那种。你看日本有尼康,佳能,索尼,都做相机,大家都过得很滋润。别看一堆厂,其实真正控制的是后面的那几个财团——有些竞争对手,后面其实是一家人。
--------------------------------- 原创文章 By
博弈和最高位
---------------------------------