数据挖掘学习——支持向量机（SVM）

目录

1.概论

（1）线性可分支持向量机                                                                       

   1.原始问题：

   2.SVM

   3.分类预测可靠度

   4.分类间隔

   5.约束条件

   6.线性可分支持向量机的学习算法（最大间隔法）

   7.对偶算法

（2）线性不可分支持向量机

算法过程

（3）非线性支持向量机

1.对偶问题

2.算法

2.实战（rbf+gamma做鸢尾花分类）

---

1.概论

  SVM是一种分类模型，是一个定义在特征空间上间隔（距离）最大的线性分类器。

  基本思路：SVM将训练样本数据集表示为特征空间的点，将各个类别的训练数据使用超平面进行分隔，在预测时，输入一个新的测试数据点，若该测试数据点在特征空间的位置分布在超平面的某一侧，则判断该测试点的类别即为该侧所对应的类别。

共有三种类型的SVM：

线性可分支持向量机(硬间隔最大化)

线性不可分支持向量机（软间隔最大化）

非线性支持向量机（核技巧和软间隔最大化）

（1）线性可分支持向量机                                                                       

  1.原始问题：

将求解线性可分支持向量机的最优化问题作为原始最优化问题。 

（SVM通常用于二分类问题，用-1和+1分别表示对应的两个类别，当yi=-1时称样本点xi为负例，当yi=+1时称样本点xi为正例）

   2.SVM

    当训练数据集为线性可分时，SVM算法期望能够在样本数据分布的特征空间中计算得到一个分离超平面，使得所有的样本（正例和负例）都可以按照其对应的类别，分布到超平面两侧。

   线性可分支持向量机的分类决策函数f(x)：

   通过间隔最大化或等价地求解相应的凸二次规划问题学习得到的分离超平面为：

  3.分类预测可靠度

   在使用SVM对训练样本进行分类时，通常采用分类预测可靠度来评估非标类算法的可靠程度。

  距离分离超平面越近，该数据的分类越不可靠，反之，距离越远，该数据的分类越可靠。

  若w·xi+b的算术符号与样本数据点的分类标签yi的符号一致，则表示分类正确，反之则分类错误。

  4.分类间隔

定义训练数据集T与超平面之间的几何间隔为：

支持向量机的目标是：找出一个能正确划分训练样本数据集，且其几何间隔最大化的分离超平面。

 （图中，虚线穿过的点即支持向量，支持向量到实线的垂直距离即为分类间隔 γ）

5.约束条件

两个问题：

（1）如何判断分离超平面是否将样本点正确分类

（2）要求解分类间隔d，需要先找到支持向量，那么如何在众多训练样本中找到支持向量呢？

这两个问题就是求解最优分类间隔的约束条件，即求解最优分离超平面的约束和限制。

6.线性可分支持向量机的学习算法（最大间隔法）

输入：输入待训练的线性可分样本数据集T。

输出：输出最大间隔的分离超平面和分类决策函数。

算法过程：

（1）求解约束和限制条件下的最优化问题

（2）求解最优解（w*，b*）

（3）得到最优化的分离超平面w*·x+b*=0及其分类决策函数f(x)=sign(w*·x+b*)

7.对偶算法

采用拉格朗日方程的主要目的在于，将约束条件放到目标函数中，从而将有约束的最优化问题转换为无约束的新的目标函数的最优化问题。

通过拉格朗日对偶，将原始问题转换为求极大极小问题。

（2）线性不可分支持向量机

算法过程：

输入：输入待训练的样本数据集T和惩罚参数C

输出：输出软间隔最大化的分离超平面和分类决策函数

（1）求解约束最优化问题

（2） 计算

同时选择a*的某个分量aj*，计算

（3）得到软间隔最大化的分离超平面和分类决策函数

（3）非线性支持向量机

1.对偶问题

核函数将输入空间中的任意两个向量x，z映射为特征空间中对应的向量之间的内积。这种将内积替换成核函数的方式称为核技巧。

在非线性支持向量机中，常用的核函数：

（1）多项式核函数

（2）高斯（Gauss）核函数

（3）sigmoid核函数

2.算法

输入：输入训练数据集T和惩罚参数C>0

输出：输出分类决策参数

算法过程：

（1）选择适当的核函数K(x,z)，求解约束最优化问题

（2）计算

同时选择a*的某个分量aj*，计算

 （3）分类决策函数为

2.实战（rbf+gamma做鸢尾花分类）

代码：

from sklearn import datasets
import numpy as np
from sklearn.model_selection import train_test_split
# 划分数据集为训练集和测试机
from sklearn import svm # 导入SVM

iris=datasets.load_iris()
# 导入鸢尾花数据集
data_train,data_test,target_train,target_test=train_test_split(iris.data,iris.target,test_size=0.3)
# 测试集占总数据集的0.3
svm_classifier=svm.SVC(C=1.0,kernel='rbf',
                       decision_function_shape='ovr',gamma=0.01)
# 定义一个svm对象
svm_classifier.fit(data_train,target_train)# 训练模型

score=svm_classifier.score(data_test,target_test)
# 把测试集的数据传入即可得到模型的评分
predict=svm_classifier.predict([[0.1,0.2,0.3,0.4]])
# 预测给定样本数据对应的标签



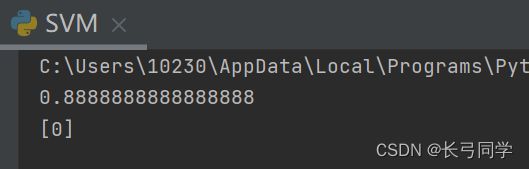
print(score)
print(predict)

参数解释：

   参数c越大，对于训练集来说，其误差越小，但更容易过拟合。

   参数coef0小，防止过拟合；coef0大，防止欠拟合。

   gamma越大，支持向量影响区域小，模型复杂度高，容易过拟合；gamma越小，决策边界趋于光滑，模型复杂度低，容易欠拟合。

   kernel参数： ‘linear’线性核函数

                        ‘poly’多项式核函数

                        ‘rbf’径向基核函数

                        ‘sigmoid’sigmoid核函数

运行结果：