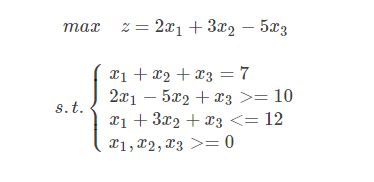数学建模代码实现

1、线性规划

  

下面是代码实现

 导入包并把约束转化成标准格式

from scipy import optimize
import numpy as np

 
c = [2, 3, -5]
A = [[-2, 5, -1], [1, 3, 1]]
b = [-10, 12]
Aeq = [[1, 1, 1]]
beq = [7]
x1 = (0, None)
x2 = (0, None)
x3 = (0, None)

LP求解函数

 
#-*- coding:utf-8 -*-
#导入包
from scipy import optimize
import numpy as np
def LP(m='',clist=[],Alist=[],blist=[],Aeqlist=[],beqlist=[],all_x=()):
    #c,A,b,Aeq,beq,LB,UB,X0,OPTIONS
    c = np.array(clist)
    A = np.array(Alist)
    b = np.array(blist)
    Aeq = np.array(Aeqlist)
    beq = np.array(beqlist)
    #求解
    if m == 'min':
        res = optimize.linprog(c, A, b, Aeq, beq, bounds=all_x)
        fun = res.fun
        x = res.x
    else:
        res = optimize.linprog(-c, A, b, Aeq, beq, bounds=all_x)
        fun = -(res.fun)
        x = res.x
    return fun,x

main函数，方便其它调用：（这个是方便写成python文件直接用命令行执行）

 
#-*- coding:utf-8 -*-
import LP
import sys
if __name__ == '__main__':
    m = sys.argv[1]
    clist = list(eval(sys.argv[2]))
    Alist = list(eval(sys.argv[3]))
    blist = list(eval(sys.argv[4]))
    Aeqlist = list(eval(sys.argv[5]))
    beqlist =list(eval(sys.argv[6]))
    all_x = tuple(eval(sys.argv[7]))
    r=LP.LP(m=m,clist=clist,Alist=Alist,blist=blist,Aeqlist=Aeqlist,beqlist=beqlist,all_x=all_x)
    print(r)

2、分支定界算法

2.1 概念

分支定界算法（Branch and bound）始终围绕着一棵搜索树进行。分支的过程就是不断给树增加子节点的过程，而定界就是在分支的过程中检查子问题的上下界，如果子问题不能产生一比当前最优解还要优的解，那么砍掉这一枝。知道所有子问题都不能产生一个更优的解时，算法结束。

 具体到整数线性规划问题，这个用来对比“叶子”是否更优，能不能被砍掉的标准就是目前最优的一套整数解，例如最小化问题，记录这套整数解的目标函数的值，这个值是最小的。任何一个枝叶解出来的目标函数如果比这个还大，下面继续分支增加约束了之后更加不能得到更优的解，所以这些所有不小于最优整数解目标函数的分支应该全部砍掉。

但是一开始很可能没有一套整数解作为标准来比较，那么对于最小化问题，这个用来参照的目标函数就是无穷大，任何一个解出来的分支不管是不是整数解都不会被砍掉。这个参照更新发生在每次出现更优的整数解时，所以现在出现任何一个整数解都要优于这个无穷大，这个解就会变成参照。

如上图，4节点得到最优解Z=10（最大问题），其他3,7,8,6节点都不能优于这个整数解，往下面继续分支添加约束只会让结果越来越差，所以找到全局最优解4节点。

 下面上代码：

import numpy
from scipy.optimize import linprog
import sys
import math

#判断是否为整数（当一个值与他的下取整或上取整相差小于1e-6时，为整数）
def judge(L, t=1e-6):
    for i in L:
        if (i-math.floor(i)) < t or (math.ceil(i)-i) < t:
            return False
    return True


def intergerpro(c, A, B, Aeq, Beq, t=1.0e-6):
    res = linprog(c, A, B, Aeq, Beq)
    if not res.success:#整数规划问题不可解时终止分支（定界）
        return [sys.maxsize]
    if judge(res.x):
        bestX = [10000]*len(c)#抄的视频上的代码，意义不明
    else:
        bestX = res.x
    bestVal = sum(x*y for x, y in zip(c, bestX))
    if all(((x-math.floor(x)) < t or (math.ceil(x)-x) < t) for x in bestX):
        return (bestVal, bestX)#整数解
    else:#加约束条件
        ind = [i for i, x in enumerate(bestX) if (x-math.floor(x) > t) and (math.ceil(x)-x) > t][0]
        newcol1 = [0] * len(A[0])
        newcol2 = [0] * len(A[0])
        newcol1[ind] = -1#新不等式约束的系数
        newcol2[ind] = 1#新不等式约束的系数
        newA1 = A.copy()
        newA2 = A.copy()
        newA1.append(newcol1)#追加新不等式约束系数
        newA2.append(newcol2)#追加新不等式约束系数
        newB1 = B.copy()
        newB2 = B.copy()
        newB1.append(-math.ceil(bestX[ind]))#新不等式约束的值
        newB2.append(math.floor(bestX[ind]))#新不等式约束的值
        r1 = intergerpro(c, newA1, newB1, Aeq, Beq)#分支
        r2 = intergerpro(c, newA2, newB2, Aeq, Beq)#分支
        if r1[0] < r2[0]:
            return r1
        else:
            return r2


c = [3, 4, 1]#问题方程
A = [[-1, -6, -2],[-2, 0, 0]]#不等式约束的系数
B = [-5, -3]#不等式约束右边的值
Aeq = [[0, 0, 0]]#等式约束（aeq与beq都为0，代表0*x1+0*x2+0*x3=0，因此这里不写这个参数也行）
Beq = [0]#等式约束值
print(intergerpro(c, A, B, Aeq, Beq))

上面的代码其实没有剪枝，bound只有整数解，把所有分支往下死里搜索知道碰到整数解。用迭代算法深度有限，抓住一个分支往下死里搜索，搜不到就死循环。最下面的分支如果是整数解就由上面return这个整数解，然后上面一层一层迭代返回那些非整数解，当然，这是它这个节点的兄弟节点也往下算清楚的情况下，返回这两个兄弟中比较牛的那个（但其实意义不大了）。结果没有整理，直接一股脑迭代输出，没时间修改了。

有机会再把代码完善了 

2、非线性规划

非线性规划可简单分为两种，目标函数为凸函数or非凸函数

凸函数的非线性规划，比如，有很多常用的库完成，比如cvxpy

非凸函数的非线性规划（求极值），可尝试一下方法：

• 纯数学方法，求导求极值
• 神经网络、深度学习（反向传播算法中链式求导过程）
• scipy.optimize.minimize(接近matlab）

scipy.optimize.minimize(fun,x0,args=(),method=None,jac=None,hess=None,hessp=None,bounds=None,constraints=(),tol=None,callback=None,options=None)

fun:求最小值的目标函数
args:常数值
method:求极值方法，一般默认
constraints:约束条件
x0:变量的初始猜测值，注意minimize是局部最优

x0初始值不同，结果可能不同，最后要经过调参的过程。可以写一个循环调参，靠算力提升结果。

昨天的代码其实是matlab，用matlab深度学习确实挺奇怪的（），参考：Matlab深度学习——入门_longlongsvip的博客-CSDN博客_matlab深度学习 

MATLAB官方深度学习入门教程：

MATLAB官方深度学习入门教程_L_fengzifei的博客-CSDN博客_matlab深度学习教程

下面继续非线性规划：

1、计算1/x+x的最小值

# coding=utf-8
from scipy.optimize import minimize
import numpy as np
 
#demo 1
#计算 1/x+x 的最小值
 def fun(args):
     a=args
     v=lambda x:a/x[0] +x[0]
     return v
 
 if __name__ == "__main__":
     args = (1)  #a
     x0 = np.asarray((2))  # 初始猜测值
     res = minimize(fun(args), x0, method='SLSQP')
     print(res.fun)
     print(res.success)
     print(res.x)

执行结果:函数的最小值为2点多，可以看出minimize求的局部最优 

 

2.计算  (2+x1)/(1+x2) - 3*x1+4*x3 的最小值  x1,x2,x3的范围都在0.1到0.9 之间

# coding=utf-8
from scipy.optimize import minimize
import numpy as np
 
# demo 2
#计算  (2+x1)/(1+x2) - 3*x1+4*x3 的最小值  x1,x2,x3的范围都在0.1到0.9 之间
def fun(args):
    a,b,c,d=args
    v=lambda x: (a+x[0])/(b+x[1]) -c*x[0]+d*x[2]
    return v
def con(args):
    # 约束条件 分为eq 和ineq
    #eq表示 函数结果等于0 ； ineq 表示 表达式大于等于0  
    x1min, x1max, x2min, x2max,x3min,x3max = args
    cons = ({'type': 'ineq', 'fun': lambda x: x[0] - x1min},\
              {'type': 'ineq', 'fun': lambda x: -x[0] + x1max},\
             {'type': 'ineq', 'fun': lambda x: x[1] - x2min},\
                {'type': 'ineq', 'fun': lambda x: -x[1] + x2max},\
            {'type': 'ineq', 'fun': lambda x: x[2] - x3min},\
             {'type': 'ineq', 'fun': lambda x: -x[2] + x3max})
    return cons
 
if __name__ == "__main__":
    #定义常量值
    args = (2,1,3,4)  #a,b,c,d
    #设置参数范围/约束条件
    args1 = (0.1,0.9,0.1, 0.9,0.1,0.9)  #x1min, x1max, x2min, x2max
    cons = con(args1)
    #设置初始猜测值  
    x0 = np.asarray((0.5,0.5,0.5))
    
    res = minimize(fun(args), x0, method='SLSQP',constraints=cons)
    print(res.fun)
    print(res.success)
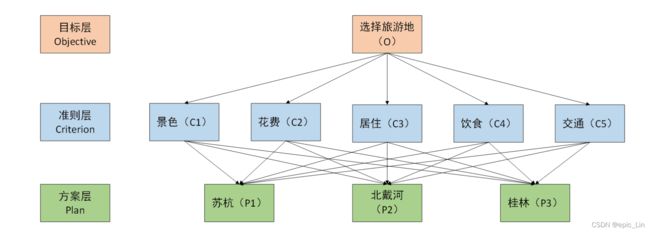
    print(res.x)

3、层次分析法

（1）一致矩阵法：

a）不把所有因素放在一起比较，而是两两相互比较

b）采用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，以提高精准度。

判断矩阵是表示本层所有因素针对上一层某一个因素的相对重要性的比较。判断矩阵的元素用Santy的1——9标度方法给出（？？？）

这里和法求列向量算术平均是针对非一致性矩阵的情况，如果是一致阵任一列向量都是特征向量就不用这么麻烦了

公式中的a是上一层的权重

 

对所有输入的矩阵都要进行层次单排序一致性检验，对层次总排序也需作一致性检验，检验仍象层次总排序那样由高层到低层逐层进行。这是因为虽然各层次均已经过层次单排序的一致性检验，各成对比较判断矩阵都已具有较为满意的一致性。但当综合考察时，各层次的非一致性仍有可能积累起来，引起最终分析结果较严重的非一致性。

 

import numpy as np
import pandas as pd
import warnings


class AHP:
    def __init__(self, criteria, samples):
        self.RI = (0, 0, 0.58, 0.9, 1.12, 1.24, 1.32, 1.41, 1.45, 1.49)
        self.criteria = criteria
        self.samples = samples
        self.num_criteria = criteria.shape[0]
        self.num_project = samples[0].shape[0]

    def calculate_weights(self, input_matrix):
        input_matrix = np.array(input_matrix)
        n, n1 = input_matrix.shape
        assert n==n1, "the matrix is not orthogonal"  # 看看长宽是否相等
        for i in range(n):
            for j in range(n):
                if np.abs(input_matrix[i,j]*input_matrix[j,i]-1) > 1e-7: # 看看是不是对称的
                    raise ValueError("the matrix is not symmetric")
        eigen_values, eigen_vectors = np.linalg.eig(input_matrix) # 计算特征值和特征向量
        max_eigen = np.max(eigen_values) # 计算最大特征值
        max_index = np.argmax(eigen_values)  # 找到最大特征值对应的索引
        eigen = eigen_vectors[:, max_index] # 找到对应的特征向量
        eigen = eigen/eigen.sum() # 归一化
        if n > 9:
            CR = None
            warnings.warn("can not judge the uniformity")
        else:
            CI = (max_eigen - n)/(n-1)  # 计算CR
            CR = CI / self.RI[n-1]
        return max_eigen, CR, eigen

    def calculate_mean_weights(self,input_matrix):
        input_matrix = np.array(input_matrix)
        n, n1 = input_matrix.shape
        assert n == n1, "the matrix is not orthogonal"
        A_mean = []
        for i in range(n):
            mean_value = input_matrix[:, i]/np.sum(input_matrix[:, i])
            A_mean.append(mean_value)
        eigen = []
        A_mean = np.array(A_mean)
        for i in range(n):
            eigen.append(np.sum(A_mean[:, i])/n)
        eigen = np.array(eigen)
        matrix_sum = np.dot(input_matrix, eigen)
        max_eigen = np.mean(matrix_sum/eigen)
        if n > 9:
            CR = None
            warnings.warn("can not judge the uniformity")
        else:
            CI = (max_eigen - n) / (n - 1)
            CR = CI / self.RI[n - 1]
        return max_eigen, CR, eigen

    def run(self, method="calculate_weights"):
        weight_func = eval(f"self.{method}")
        max_eigen, CR, criteria_eigen = weight_func(self.criteria)
        print('准则层：最大特征值{:<5f},CR={:<5f},检验{}通过'.format(max_eigen, CR, '' if CR < 0.1 else '不'))
        print('准则层权重={}\n'.format(criteria_eigen))

        max_eigen_list, CR_list, eigen_list = [], [], []
        for sample in self.samples:
            max_eigen, CR, eigen = weight_func(sample)
            max_eigen_list.append(max_eigen)
            CR_list.append(CR)
            eigen_list.append(eigen)

        pd_print = pd.DataFrame(eigen_list, index=['准则' + str(i+1) for i in range(self.num_criteria)],
                                columns=['方案' + str(i+1) for i in range(self.num_project)],
                                )
        pd_print.loc[:, '最大特征值'] = max_eigen_list
        pd_print.loc[:, 'CR'] = CR_list
        pd_print.loc[:, '一致性检验'] = pd_print.loc[:, 'CR'] < 0.1
        print('方案层')
        print(pd_print)

        # 目标层
        obj = np.dot(criteria_eigen.reshape(1, -1), np.array(eigen_list))
        print('\n目标层', obj)
        print('最优选择是方案{}'.format(np.argmax(obj)+1))
        return obj


if __name__ == '__main__':
    # 准则重要性矩阵
    criteria = np.array([[1, 2, 7, 5],
                         [1 / 2, 1, 4, 3],
                         [1 / 7, 1 / 4, 1, 1 / 2],
                         [1 / 5, 1 / 3, 2, 1]])

    # 对每个准则，方案优劣排序
    sample1 = np.array([[1, 2, 8], [1/2, 1, 6], [1/8, 1/6, 1]])
    sample2 = np.array([[1, 2, 5], [1 / 2, 1, 2], [1 / 5, 1 / 2, 1]])
    sample3 = np.array([[1, 1, 3], [1, 1, 3], [1 / 3, 1 / 3, 1]])
    sample4 = np.array([[1, 3, 4], [1 / 3, 1, 1], [1 / 4, 1, 1]])

    samples = [sample1, sample2, sample3, sample4]
    a = AHP(criteria, samples).run("calculate_mean_weights")