hdu 3694 10 福州 现场 E - Fermat Point in Quadrangle 费马点 计算几何 难度:1
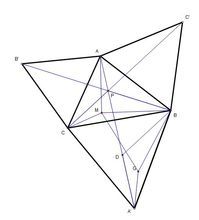
In geometry the Fermat point of a triangle, also called Torricelli point, is a point such that the total distance from the three vertices of the triangle to the point is the minimum. It is so named because this problem is first raised by Fermat in a private letter. In the following picture, P
0 is the Fermat point. You may have already known the property that:
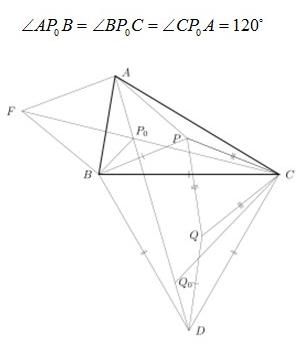
Alice and Bob are learning geometry. Recently they are studying about the Fermat Point.
Alice: I wonder whether there is a similar point for quadrangle.
Bob: I think there must exist one.
Alice: Then how to know where it is? How to prove?
Bob: I don’t know. Wait… the point may hold the similar property as the case in triangle.
Alice: It sounds reasonable. Why not use our computer to solve the problem? Find the Fermat point, and then verify your assumption.
Bob: A good idea.
So they ask you, the best programmer, to solve it. Find the Fermat point for a quadrangle, i.e. find a point such that the total distance from the four vertices of the quadrangle to that point is the minimum.

Alice and Bob are learning geometry. Recently they are studying about the Fermat Point.
Alice: I wonder whether there is a similar point for quadrangle.
Bob: I think there must exist one.
Alice: Then how to know where it is? How to prove?
Bob: I don’t know. Wait… the point may hold the similar property as the case in triangle.
Alice: It sounds reasonable. Why not use our computer to solve the problem? Find the Fermat point, and then verify your assumption.
Bob: A good idea.
So they ask you, the best programmer, to solve it. Find the Fermat point for a quadrangle, i.e. find a point such that the total distance from the four vertices of the quadrangle to that point is the minimum.
Input
The input contains no more than 1000 test cases.
Each test case is a single line which contains eight float numbers, and it is formatted as below:
x 1 y 1 x 2 y 2 x 3 y 3 x 4 y 4
x i, y i are the x- and y-coordinates of the ith vertices of a quadrangle. They are float numbers and satisfy 0 ≤ x i ≤ 1000 and 0 ≤ y i ≤ 1000 (i = 1, …, 4).
The input is ended by eight -1.
Each test case is a single line which contains eight float numbers, and it is formatted as below:
x 1 y 1 x 2 y 2 x 3 y 3 x 4 y 4
x i, y i are the x- and y-coordinates of the ith vertices of a quadrangle. They are float numbers and satisfy 0 ≤ x i ≤ 1000 and 0 ≤ y i ≤ 1000 (i = 1, …, 4).
The input is ended by eight -1.
Output
For each test case, find the Fermat point, and output the total distance from the four vertices to that point. The result should be rounded to four digits after the decimal point.
Sample Input
0 0 1 1 1 0 0 1 1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1
四边形费马点
平面四边形中费马点证明相对于三角形中较为简易,也较容易研究。
(1)在
凸四边形ABCD中,费马点为两对角线AC、BD交点P。
(2)在
凹四边形ABCD中,费马点为凹顶点D(P)。
经过上述的推导,我们即得出了三角形中费马点的找法:当三角形有一个内角大于或等于120°的时候,费马点就是这个内角的顶点;如果三个内角都在120°以内,那么,费马点就是使得费马点与三角形三顶点的连线两两夹角为120°的点。另一种更为简捷的证明 :设O为三顶点连线最短点,以A为圆心AO为半径做圆P。将圆P视作一面镜子。显然O点应该为B出发的光线经过镜子到C的反射点(如果不是,反射点为O',就会有BO’+ CO' < BO+ CO,而AO’= AO,就会有 AO’+ BO’+ CO' < AO + BO + CO)。
(补充说明:AO、BO、CO是每个镜子的法线)
取四个点其中一个点或者四个点两两连线的交点,各算一遍即可
感受:赛场上没有及时证明猜想,导致smilewsw一直不敢敲...,几何证明实力太弱,虽然想到镜面反射来证最短,但是没有具体转化
这是萌萌smilewsw代码
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
const double eps=1e-10;
double add(double a,double b)
{
if(abs(a+b)<eps*(abs(a)+abs(b))) return 0;
return a+b;
}
struct point
{
double x,y;
point () {}
point (double x,double y) : x(x),y(y){ }
point operator + (point p)
{
return point (add(x,p.x),add(y,p.y));
}
point operator - (point p)
{
return point (add(x,-p.x),add(y,-p.y));
}
point operator * (double d)
{
return point (x*d,y*d);
}
double dot(point p)
{
return add(x*p.x,y*p.y);
}
double det(point p)
{
return add(x*p.y,-y*p.x);
}
};
bool on_seg(point p1,point p2,point q)
{
return (p1-q).det(p2-q)==0&&(p1-q).dot(p2-q)<=0;
}
point intersection(point p1,point p2,point q1,point q2)
{
return p1+(p2-p1)*((q2-q1).det(q1-p1)/(q2-q1).det(p2-p1));
}
bool cmp_x(const point&p,const point& q)
{
if(p.x!=q.x) return p.x<q.x;
return p.y<q.y;
}
vector<point> convex_hull(point*ps,int n)
{
sort(ps,ps+n,cmp_x);
//for(int i=0;i<n;i++) printf("x=%.f %.f")
int k=0;
vector<point> qs(n*2);
for(int i=0;i<n;i++){
while(k>1&&(qs[k-1]-qs[k-2]).det(ps[i]-qs[k-1])<=0) k--;
qs[k++]=ps[i];
}
for(int i=n-2,t=k;i>=0;i--){
while(k>t&&(qs[k-1]-qs[k-2]).det(ps[i]-qs[k-1])<=0) k--;
qs[k++]=ps[i];
}
qs.resize(k-1);
return qs;
}
double dis(point p1,point p2)
{
return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
bool equ(point p1,point p2)
{
if(fabs(p1.x-p2.x)<eps&&fabs(p1.y-p2.y)<eps)
return true;
return false;
}
int main()
{
point p[10];
for(int i=0;i<4;i++)
scanf("%lf%lf",&p[i].x,&p[i].y);
while(p[0].x!=-1&&p[0].y!=-1)
{
vector <point> m;
double minn=100000000,d;
m=convex_hull(p,4);//检查是否四边形
if(m.size()==4)//如果是四边形则加入对角线交点考虑
minn=dis(m[1],m[3])+dis(m[0],m[2]);
for(int i=0;i<4;i++)
{
d=0;
for(int j=0;j<4;j++)
d+=dis(p[i],p[j]);
minn=min(minn,d);
}
printf("%.4f\n",minn);
for(int i=0;i<4;i++)
scanf("%lf%lf",&p[i].x,&p[i].y);
}
return 0;
}