Anomaly Detection（异常检测）的原理及最新的技术应用（李宏毅视频课整理和总结）

---

0 前言

本节学习的是Anomaly Detection（异常检测），即让一个系统从数据中学习到某些正常的特征，从而能够诊断出非正常的数据。本文由整理李宏毅老师视频课笔记和个人理解所得，详细讲述了Anomaly Detection的原理及最新的技术。我会及时回复评论区的问题，如果觉得本文有帮助欢迎点赞 。

1 Introduction

1.1 Problem Formulation

Anomaly Detection从定义而言就是一种识别不正常情况与挖掘非逻辑数据的技术。简而言之，让机器能自己监测到自己的异常。例如在计算机视觉的应用中，有人在边骑车边打电话，那这就是个不符合规范的，我们能否采用一些方式来将其检测出来。通常情况下，在我们阅读论文的过程中，异常检测(Anomaly Detection)也被叫做，Novelty Detection，Outlier Detection，Forgery Detection，Out-of-distribution Detection。

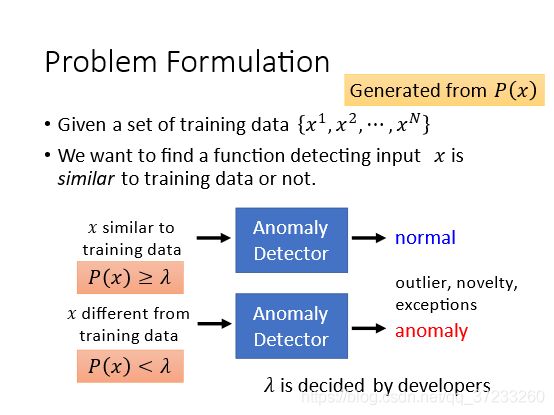
假设给定一组训练数据$\left\{x^1,x^2,\cdots ,x^N\right\}$，期望找到一个函数使得当输入另外的$x$的时，可以检测这个数据和训练数据是否相似，否则就是异常数据，总之就是和训练数据不一样的数据。

异常是相对于训练数据而言的：

有一些应用，例如信用卡盗刷，超大金额支出的检测等等：

1.2 Base Idea

最简单的想法是用一组正常的数据$\left\{x^1,x^2,\cdots ,x^N\right\}$和一组异常的数据$\left\{{\tilde{x}}^1,{\tilde{x}}^2,\cdots ,{\tilde{x}}^N\right\}$，一起训练一个二分类的分类器。但是有个问题是异常数据并不是一种类型，无法视为一个class，只要是非正常的都是异常，如下图所示。而且实际中的异常数据也是小概率事件的，比如网络攻击，比如诈骗交易，会有正负样本不均匀的情况：

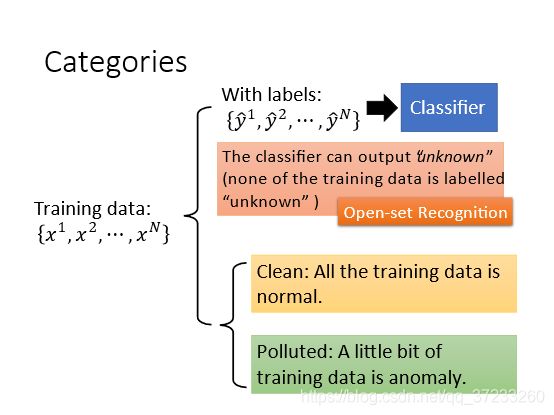
给定训练数据，并且带有某种类型的label$\left\{{\hat{y}}^1,{\hat{y}}^2,\cdots ,{\hat{y}}^N\right\}$，使用这些数据先训练一个classifier。数据和label中并没有unknown，但是期望classifier在遇到一个未知数据时能给出unknown的判定。也被称为Open-set Recognition。

还有一种是训练数据是没有标签的，通过相似度来判断异常数据。这里面又分两种情况，一种是训练数据是clean，一种是polluted。

2 With Classifier

2.1 Base Method

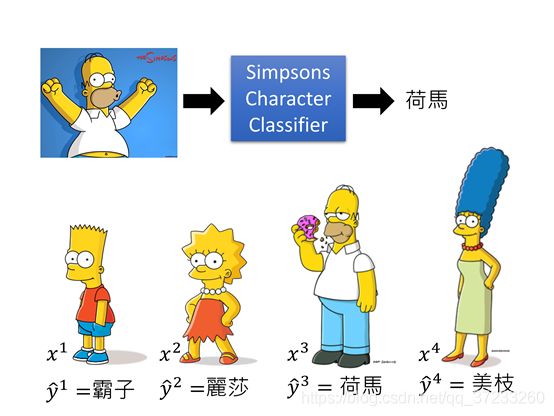
给定一组Simpsons家族人物的数据，判断$x$是否来自该家族：

而且这些数据都是有label的，可以训练一个Simpsons的家族分类器，输入人物图片，可以输出名字：

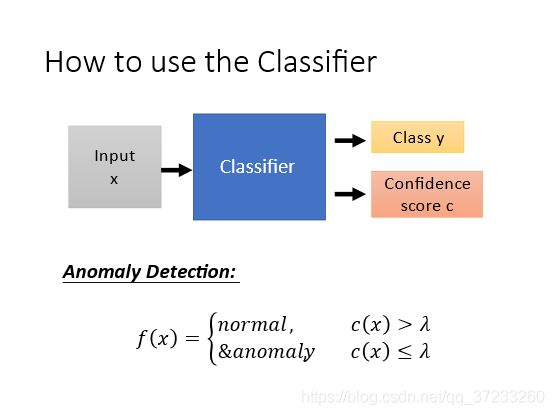
有了Classifier之后，期望使用这个来做异常侦测。输入一个人物，判断其是否属于Simpsons家庭。做法是输入$x$之后，输出$y$的同时输出一个信心分数$c$，通过和设置的阈值$\lambda$进行比较来判断是否异常，小于则是异常：

development set：用于训练过程中，指导调整超参数的样本集，使用起来类似于测试集。这个数据集中有labelled正常数据和异常数据。计算模型在这个数据集上的效果，来调整阈值lamda和其他超参数。

具体举例如下。当输出概率比较集中，最高的分数比较高的时候就是正常；概率比较平均，最高分数比较低就是异常：

也可以使用熵值或者其他方式来描述。

老师做了实验，结果也可以得到验证：

只是机器常常会把异常图片辨别为“柯阿三”这个人物，因为这个人物本身就和其他正常数据差距略大：

2.2 Evaluation

那么怎么评估模型的好坏呢？ 给定100张正常simpsons家族图片和5张其他动漫图片，得到了以下结果。蓝色表示simpsons家族的得分，红色表示其他动漫的得分。因为样本不均衡的原因，所以使用accuracy是不准确的，因为负样本只有5个，对accuracy几乎无影响。

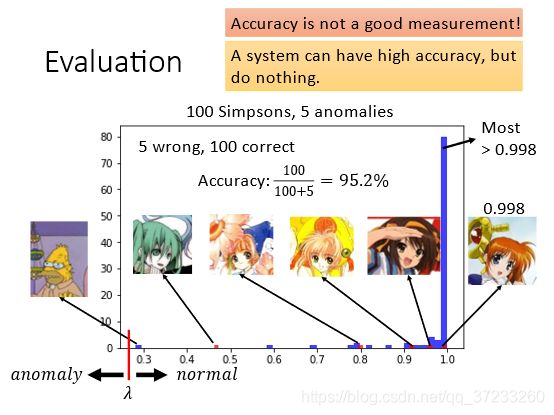
假设lamda设置在0.5-0.6之间，可以得到如下的混淆矩阵：

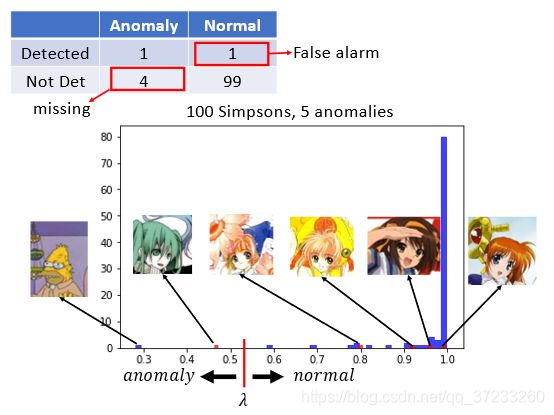
如果设置在0.8-0.9可以得到另外的混淆矩阵：

假阴性和假阳性都是我们不需要的，但是到底哪一个更重要，可以根据实际情况进行权重的调整。不同的任务，计算cost的方式也不一样：

2.3 More

2.3.1 Possible Issues

但是刚刚的方法也有一些问题。比如假设有一个classifier，可以区别猫和狗。classifier对于输入比如食蚁兽和羊驼来说，确实可以检测出他们是异常数据。但是对于老虎和狼，这些生物在猫和狗的特征上特别强烈，以至于classifier很难将它们挑出来。

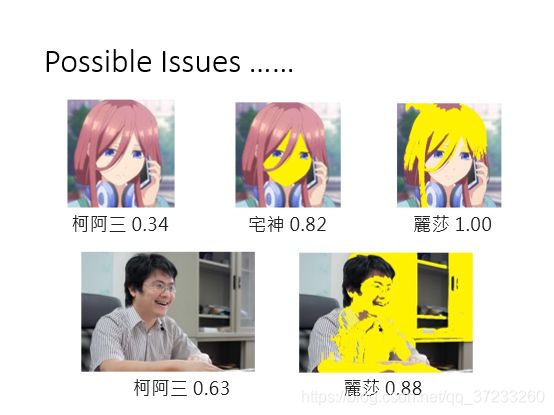
所以会不会某些特征，比如颜色，会特别影响分类结果呢？老师将一些图片涂黄之后就会使得识别为simpsons家族的概率提高：

2.3.2 Network for Confidence Estimation

刚刚那种方法虽然简单，但是效果是不错的。还有另外一种更好的方法，即学习一个网络可以直接输出信心分数：

2.3.3 Obtain Anomaly

异常数据是难以获得的，所以有人考虑一种生成器可以生成一些异常资料：

3 Without Labels

就是指的训练数据是没有标签的。假设很多人可以同时操作一个游戏角色，那么多数玩家都是期望游戏可以正常进行的，而假设存在一些玩家恶意阻止游戏进行，那么考虑怎样检测出来。给定一组训练数据，给定input $x$，$x$每个维度代表玩家的某种行为：

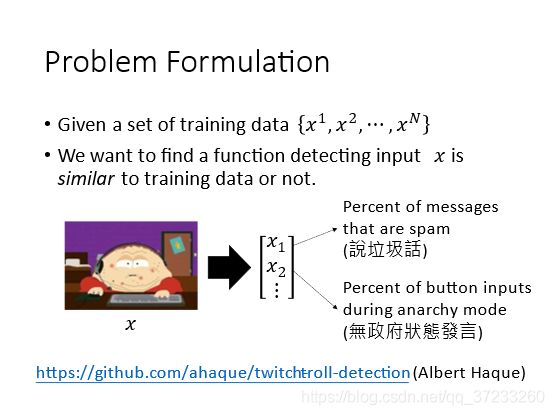
同样的，输入x，可以判断是否为异常数据。但是这里已经没有classifier了，所以使用了一个几率函数P来判断：

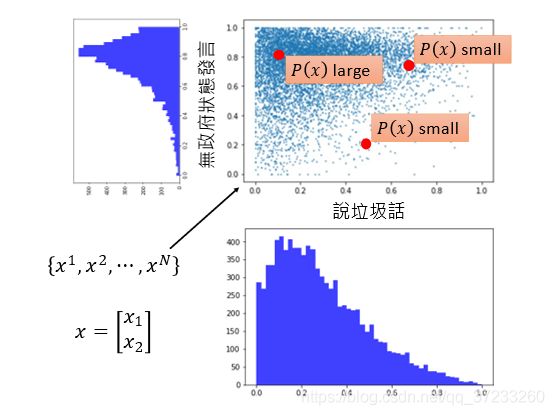
因为玩家的行为是可以统计的，假设有两个维度，可以获得不同玩家行为的概率分布。直观上可以感知哪些位置概率高，哪些概率低，但是仍然需要数值化的方法：

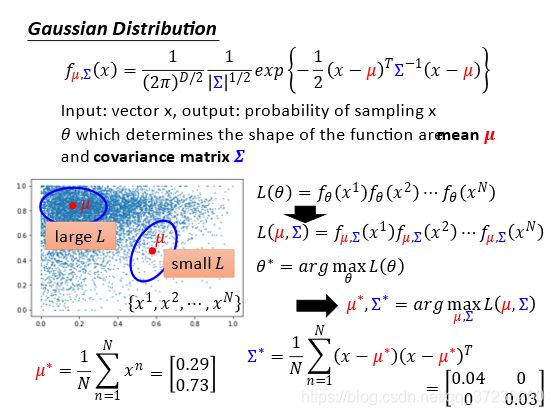
假设给定一种概率密度函数可以描述数据的分布，其参数$\theta$（指代所有的参数）是未知的，那么可以通过极大似然估计来获取参数的值。选择不同的$\theta$值可以算出不同的似然值，而我们需要一组$\theta$使得似然最大。

使用高斯分布举例，参数就是均值和方差，也就是我们关注的$\theta$参数。穷举所有的可能值，计算极大似然值，最佳的均值和方差：

当然这里有一个非常强的假设，即数据分布满足高斯分布。实际上一般也不见得满足，但是高斯分布用的十分广泛，有人说人的很多行为都是满足高斯的，即使不是，也很类似。所以基本上用高斯的效果都还不错。

参数可以很方便的求解：

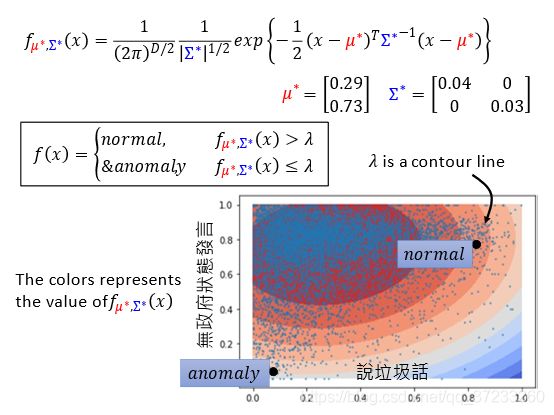
现在可以使用概率值来计算了，$\lambda$就是图上的等高线：

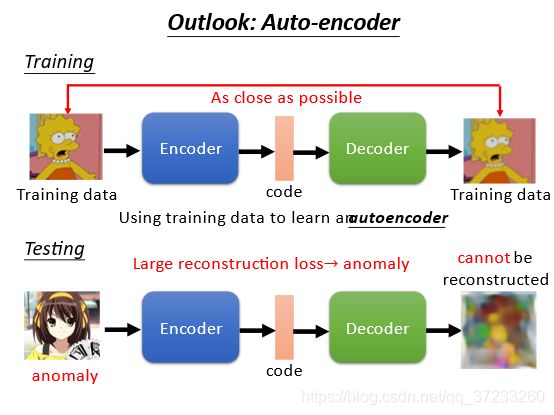
训练一个auto-encoder来做异常检测，可以根据对图片的还原度来判断是否为异常数据：