PyTorch 入门与实践（六）卷积神经网络进阶（DenseNet）

来自 B 站刘二大人的《PyTorch深度学习实践》P11 的学习笔记

上一篇 卷积神经网络进阶（GoogLeNet、ResNet） 我们实践了 GoogleNet 和 ResNet 两大经典网络：

• GoogleNet 从多路选择学习（Inception Module）出发，构建更好的神经网络；
• ResNet 从残差连接（Residual Block）保留浅层特征出发，构建更深的神经网络。

DenseNet¹ 紧随其后，再次研究了超深度神经网络的梯度消失问题和跳连解决方案。他们提到，ResNet 等的方法尽管在神经网络拓扑和训练过程上有所不同，但它们都有一个关键特征：使用短路径连接前后两层。

DenseNet 结构

DenseNet 更加偏执，为了确保网络在深度传播中能保留更多信息，他们不仅连接前后两层，在一个 Dense Block 中每一层都和后面所有层相连，并且是将特征在通道上堆叠再传入下一层（像 Inception Module 的输出），而不是 ResNet 那样的元素相加。

这当然能保留更多信息，不过这显存消耗可想而知，这就是为什么它叫 Dense，一个 L 层的 Dense Block 有 $\frac{L(L+1)}{2}$ 条连接。

一、Dense Block

每个 Dense Block 里的卷积层都是 3×3 卷积，下表第三列乘号后面的数表示一个 Dense Block 中有多少层这样的卷积。

• Bottleneck Layers
  在每个 3×3 卷积之前引入 1×1 卷积作为瓶颈层，可以减少输入特征的通道数，从而提高计算效率。

所以，如果 Dense Block 里面是 1×1 卷积和 3×3 卷积的组合，那么这些 Dense Blocks 组成的 DenseNet 被称为 DenseNet-B。

二、Transition Layer

当然，为了控制显存占用，DenseNet 主要结构除了这 Dense Block 外还有每个 Block 后连接的过渡层（Transition Layer），它通过一个 1×1 的卷积层来控制通道数，并使用平均池化来减半特征图的高和宽。

所以，Dense Blocks 之间存在过渡层，那么这些 Dense Blocks 组成的 DenseNet 被称为 DenseNet-C。

两者都存在的 DenseNet，称为 DenseNet-BC，这是 DenseNet 的终极配置。。。

三、Growth Rate

增长率 $k$，它表示每一个卷积层输出的通道数。论文中说：设 $k_0$ 是初始输入的图像的通道数，那么 $l$ 层的 Dense Net 就会产生 $k_0+k(l-1)$ 个通道的特征图，这个 $k$ 就被称为增长率。

这表示通道数“爆炸”速度，但是多搞一个新名字出来吓唬人，我们当然可以直接说这是每个卷积层输出的通道数：$out\_channels$，但是在代码实现过程中你就能发现，这个 $k$ 要作为系数用于计算 Dense Block 中每一层卷积的输入通道，所以把输出通道称为增长率，着实细节！

利用 Bottleneck layer，Translation layer 以及较小的 Growth rate 使得网络变窄，参数减少，有效抑制了过拟合，同时计算量也减少了²。

DenseNet 最后的分类器使用全局平均池化接一层全连接层。

四、Implementation Details

对于图像较小的数据集，比如 CIFAR-10/100、SVHN，DenseNet 由 3 个 Dense Block 组成。

• 在输入第一个 Dense Block 之前先经过一个 padding=1 的 3×3 卷积，输出 32 通道；
• 使用 DenseNet-BC 配置，在每个 Dense Block 之间加入过渡层，使特征图通道数和宽高减半；
• 在最后一个 Dense Block 的末尾，执行全局平均池化，然后连接 Softmax 分类器。

输入 3 个 Dense Block 中的特征图大小分别为：32×32、16×16、8×8。采用 $\{L=40,k=12\}$ 的 DenseNet-BC 配置。

五、代码实现

• conv_block 是 Dense Block 的基础结构，包含一层 3×3 卷积的 basic_block，和一层可选的 1×1 卷积的 bottleneck：

  关于 nn.Sequential 可以查阅官方文档，里面举的例子十分清晰易懂。

  from collections import OrderedDict
  import torch
  from torch import nn
  
  def conv_block(in_channels, out_channels, bo=True):
      """
      Dense Block 的基本组件, 一层 3×3 卷积和一层可选的 1×1 卷积
      :param in_channels:
      :param out_channels: growth rate k
      :param bo: 是否使用 bottleneck
      :return: 一个 conv_block
      """
      # 有无 bottleneck 会影响下面 3×3 卷积的输入通道数，所以要判断一下
      in_channels_ = out_channels * 2 if bo else in_channels
  
      bo_layers = nn.Sequential(OrderedDict([
          ('bn0', nn.BatchNorm2d(in_channels)),
          ('relu0', nn.ReLU()),
          ('conv1x1', nn.Conv2d(in_channels, in_channels_, kernel_size=1)),
      ]))
  
      basic_blk = nn.Sequential(OrderedDict([
          ('bn1', nn.BatchNorm2d(in_channels_)),
          ('relu1', nn.ReLU()),
          ('conv3x3', nn.Conv2d(in_channels_, out_channels, kernel_size=3, padding=1)),
      ]))
  
      # 如果不用 bottleneck 可以传入一个空的 Sequential
      bottleneck = bo_layers if bo else nn.Sequential()  
  
      blk = nn.Sequential()
      blk.add_module('bottleneck', bottleneck)
      blk.add_module('basic_blk', basic_blk)
      return blk
  

• Dense Block

  当前 conv_block 的输入是前面所有 conv_block 的输出堆叠起来的，所以第 $l$ 层的输入通道数为：
  $$k_0+k\times (l-1)$$
  $k_0$ 是初始输入层的通道数 $k$ 就是上面提到的 Growth Rate，也就是 conv_block 中每个卷积层的输出通道数 out_channels。

  def dense_block(in_channels, conv_blk_num=4, k=12, bo=True):
      """
      dense_block 由上面多个 conv_block 组成，用 for 循环添加到 nn.Sequential() 中
      :param in_channels:
      :param conv_blk_num: 3×3卷积层个数
      :param k: = out_channels，每个3×3卷积层的输出通道数
      :param bo: 是否加入 bottleneck
      :return: 一个 dense_block
      """
      dense_block = nn.Sequential()
      for i in range(conv_blk_num):
          # 当前 conv_block 的输入是前面所有 conv_block 的输出堆叠起来的，所以输入通道数按照论文中这个公式变化
          in_channels_ = in_channels + i * k
          dense_block.add_module(f'conv_blk_{i}', conv_block(in_channels_, k, bo=bo))
      
      return dense_block
  

• transition_layer 是 Dense Block 之间的过渡层，用 1×1 卷积减少 Dense Block 的输出通道数，否则会越叠越多，导致内存爆炸：

  def transition_layer(input, in_channels, out_channels):
      """
      过渡层，在 Dense Block 和 Dense Block 之间，把前一个的输出通道减半
      :param in_channels: 前一个的输出通道
      :param out_channels: 输出通道减半
      :return:
      """
      device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")  # 有 cuda 则使用 GPU
      blk = nn.Sequential(OrderedDict([
          ('bn', nn.BatchNorm2d(in_channels)),
          ('relu', nn.ReLU()),
          ('conv1x1', nn.Conv2d(in_channels, out_channels, kernel_size=1)),
          ('avgpool', nn.AvgPool2d(2))
      ]))
      blk.to(device)
      return blk(input)
  

• 我们可以先试验一个多层 1×1 和 3×3 卷积组成的 Dense Block 的网络结构和输出特征图的形状：

  def forward(x, model, transition=True):
      for i, blk in enumerate(model):
          # 遍历 dense block 的每一层卷积，把它们的输出都堆叠起来
          print(i)
          y = blk(x)
          x = torch.cat((x, y), dim=1)
          print(x.shape)
  
      if transition:
          x = transition_layer(x, x.shape[1], x.shape[1]//2)
      print("x final size:", x.shape)
  
      return x
  
  if __name__ == '__main__':
      in_channels = 16
      input = torch.randn(1, in_channels, 28, 28)  # (mini-batch, channels, H, W)
      # print(input.shape)
  
      # bo=True 则加入 bottleneck，用1×1卷积减少3×3卷积的运算通道
      dense_block = dense_block(in_channels=in_channels, conv_blk_num=4, k=12, bo=True)
      print(dense_block)  # 打印网络结构
      # transition=True 则把 dense_block 的输出减半
      output_dense = forward(input, model=dense_block, transition=False)
  

• DenseNet 的基础结构由 3 个 Dense Blocks 以及可选的 Dense Block 之间的过渡层（Transition layers）组成，这些可选组件都可以通过参数来设定，因为我们已经全部实现了：

  from collections import OrderedDict
  import torch
  from torch import nn
  from torch.nn import functional as F
  
  def transition_layer(input, in_channels, out_channels):
      """
      过渡层，在 Dense Block 和 Dense Block 之间，把前一个的输出通道和长宽减半
      :param in_channels: 前一个的输出通道
      :param out_channels: 输出通道减半
      :return:
      """
      device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")  # 有 cuda 则使用 GPU
      blk = nn.Sequential(OrderedDict([
          ('bn', nn.BatchNorm2d(in_channels)),
          ('relu', nn.ReLU()),
          ('conv1x1', nn.Conv2d(in_channels, out_channels, kernel_size=1)),
          ('avgpool', nn.AvgPool2d(2))
      ]))
      blk.to(device)
      return blk(input)
  
  
  def conv_block(in_channels, out_channels, bo=False):
      """
      Dense Block 的基本组件
      :param in_channels:
      :param out_channels: growth rate k
      :return:
      """
      in_channels_ = out_channels * 2 if bo else in_channels
  
      bo_layers = nn.Sequential(OrderedDict([
          ('bn0', nn.BatchNorm2d(in_channels)),
          ('relu0', nn.ReLU()),
          ('conv1x1', nn.Conv2d(in_channels, in_channels_, kernel_size=1)),
      ]))
  
      basic_blk = nn.Sequential(OrderedDict([
          ('bn1', nn.BatchNorm2d(in_channels_)),
          ('relu1', nn.ReLU()),
          ('conv3x3', nn.Conv2d(in_channels_, out_channels, kernel_size=3, padding=1)),
      ]))
  
      bottleneck = bo_layers if bo else nn.Sequential()
  
      blk = nn.Sequential()
      blk.add_module('bottleneck', bottleneck)
      blk.add_module('basic_blk', basic_blk)
      return blk
  
  
  class DenseBlock(nn.Module):
      """
      由 conv_blk 组成
      :param in_channels: 动态的，由上一个 Dense Block 和过渡层决定
      :param out_channels: growth rate k
      :param dense_blk_num: 由多少 conv_blk 组成一个 Dense Block
      """
      def __init__(self,
                   in_channels,
                   out_channels,
                   conv_blk_num=4,
                   bo=False,
                   transition=True):
          super(DenseBlock, self).__init__()
          self.transition = transition
          self.net = nn.Sequential()
          
          for i in range(conv_blk_num):
              # 要多少就加多少
              in_channels_ = in_channels + i * out_channels
              self.net.add_module(f'conv_blk_{i}',
                                  conv_block(in_channels_, out_channels, bo))
  
      def forward(self, x):
          for blk in self.net:
              y = blk(x)
              x = torch.cat((x, y), dim=1)
          if self.transition:
              out_channels = x.shape[1]
              x = transition_layer(x, out_channels, out_channels // 2)
          print(x.shape)
          return x
  
  
  class DenceNet(nn.Module):
      """
      由 Dense Block 组成
      :param in_channels: 3-cifar-10, 1-mnist
      :param out_channels: growth rate k
      :param dense_blk_num: 由多少 Dense Block 组成
      """
      def __init__(self,
                   in_channels=16,
                   out_channels=12,
                   conv_blk_num=4,
                   dense_blk_num=3,
                   bo=False,
                   transition=True):
          super(DenceNet, self).__init__()
          self.bn0 = nn.BatchNorm2d(3)
          self.conv0 = nn.Conv2d(3, 16, kernel_size=3, padding=1)
  
          self.dense_net = nn.Sequential()
          in_channels_ = in_channels
          for i in range(dense_blk_num):
              # 计算通道数，有点绕，想搞清楚可以手动遍历
              in_channels_ += conv_blk_num * out_channels if i > 0 else 0
              in_channels_ = in_channels_ // 2 if i > 0 else in_channels_
              print("in_channels_:", in_channels_)
  
              if transition:
                  self.is_transition = dense_blk_num - 1 - i  # 最后一个 dense Block 不用接过渡层
  
              self.dense_net.add_module(f"dense_blk_{i}",
                                        DenseBlock(in_channels_,
                                                   out_channels,
                                                   conv_blk_num=conv_blk_num,
                                                   bo=bo,
                                                   transition=self.is_transition))
          self.aap = nn.AdaptiveAvgPool2d(10)  # 全局平均池化，输出 10×10
          self.fc = nn.Linear(8800, 10)
  
      def forward(self, x):
          batch_size = x.size(0)
  
          x = self.conv0(F.relu(self.bn0(x)))  # N,16,,
          x = self.dense_net(x)
          x = self.aap(x)
          x = x.view(batch_size, -1)  # batch×通道数×10×10=8800
          x = F.softmax(self.fc(x))
          return x
  
  if __name__ == '__main__':
      # 模拟数据输入网络
      in_channels, k = 16, 12
      model = DenceNet(in_channels=in_channels,
                       out_channels=k,
                       conv_blk_num=4,  # 每个Dense Block中的3×3卷积个数
                       dense_blk_num=3,  # 每个DenseNet包含的Dense Block个数
                       bo=False,
                       transition=True
                       )
      print(model)
      input = torch.randn(1, 3, 32, 32)
      output = model(input)
      print("final x shape:", output.shape)
  

Tips：在不知道全连接层接收的参数到底为多少的情况下（比如，这里的8800），我们可以注释掉 self.fc() 的调用，然后构造和训练数据集一个 mini-batch 相同大小的数据作为 input，得到的输出很轻易能告诉你答案。

六、实验结果

完整代码参见：dense_net.py
DenseNet 参数量不大，相同深度比 ResNet 的参数还少，这是参数共享的好处，但不断堆叠的特征导致了内存消耗很大，训练要很久。

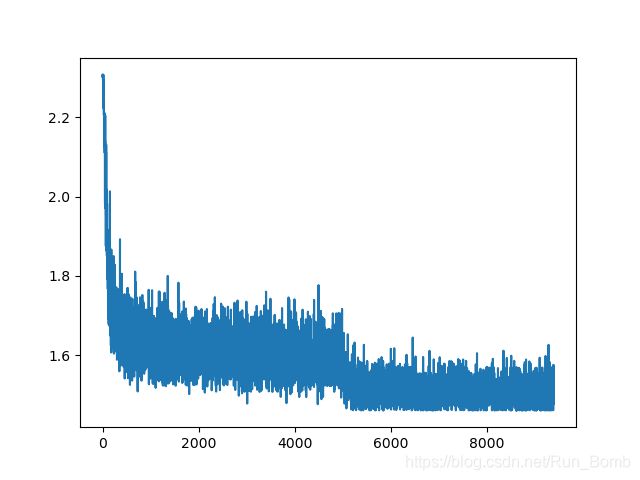
下面是我用 Tesla T4 GPU 在 MNIST 数据集上训练 10 个 epochs 的实验结果，训练精度 0.96，后面的在测试集上的测试精度也是 0.96，至少说明没有过拟合，盲猜再多训练 10 个 epochs 能达到最佳。

• 训练精度和 loss 曲线
  
  

• 预测结果
  

---

1. Huang, Gao, et aI. “Densely Connected Convolutional Networks.” IEEE Conference on Computer Vision Pattern Recognition (2017): 2261-69. ↩︎

2. DenseNet算法详解 ↩︎