（pytorch进阶之路）交叉熵、信息熵、二分类交叉熵、负对数似然、KL散度、余弦相似度

CE loss

torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=- 100, reduce=None, reduction='mean', label_smoothing=0.0)

weight：权重，对不同类别均衡
ignore_index：目标为igonre_index的话不纳入loss值中

CE loss 一般用在分类任务中

交叉熵：用一个分布去衡量另外一个分布所需要的bit数目
H(p,q) = - ∑ p(x) log(q(x))

p（x)一般为1，one-hot的形式，只在一个概率上为1，其他位置为0，因此p（x)对应着1，其他0位置的地方就不做计算了，q（x）对应模型预测到那个类别的概率

知识蒸馏和暗标签，大模型预测出的结果作为小模型的输入，这个分布就不是1分布的one-hot标签了。此时的公式计算就是要对所有的类别做计算

关于reduction参数是是否做平均，有mean和sum

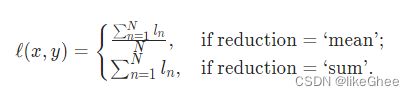
C是class，类别数目
调用传入input [C]，[N,C] ， [N,C,…] 时空维放后面比如C后面依次是H，W，channel，T，把分类维度C放在第二维度，后面的维度多少维都没问题，注意这里的input是未归一化的，也就是没有进行softmax

target可以传入一个整型，一个类别的标签，如果输入是[N,C],则传入[N]，如果输入传入的是[N,C,…] ，则target为[N,…]，target少了C ，此时target是delta目标分布

target传入的值域是在0到C-1之间，当然也可以设置成input一样的形状，比如在知识蒸馏和暗标签的时候，不过这个时候的值域是在0到1之间的浮点型

import torch
import torch.nn as nn
import torch.nn.functional as F

bs = 2
num_class = 4

logits = torch.randn(bs, num_class)
target_logits = torch.randn(bs, num_class)
target = torch.randint(num_class, size=[bs, ])

# 调用ce loss
ce_loss_fn = nn.CrossEntropyLoss()
ce_loss = ce_loss_fn(logits, target)
print(f"cross entropy loss:{ce_loss}")
ce_loss = ce_loss_fn(logits, torch.softmax(target_logits, dim=-1))
print(f"cross entropy loss:{ce_loss}")

负对数似然

NLL Loss

torch.nn.NLLLoss(weight=None, size_average=None, ignore_index=- 100, reduce=None, reduction='mean')

调用的参数基本和CELoss一致

如果用NLL forward函数调用的话，input是包含每个类别的对数概率，是做了对数化的

target是类别的索引，值域在0到C-1之间，target不提供浮点型的输入，因此target的维度始终比输入少一维

计算公式：
xn就是对数化数据，weight乘以1函数delta分布

nll_loss_fn = nn.NLLLoss()
# 因为nll要输入的是归一化后的对数logits,对最后一维做softmax和log
nll_loss = nll_loss_fn(torch.log(torch.softmax(logits, dim=-1) + 1e-7), target_index)
print(f"negative log-likelihood loss: {nll_loss}")

发现它的结果CE loss几乎一致，那么CE和NLL之间可以根据网络自行选择损失函数

KL散度

kullback leibler divergence 预测分布与目标分布距离的度量
torch.nn.KLDivLoss(size_average=None, reduce=None, reduction='mean', log_target=False)
交叉熵 = 信息熵 + KL散度

参数log_target：如果target是log形式的化把它置为True

KL散度的公示：L（y_pred, y_true） = Dkl（y_true，y_pred）

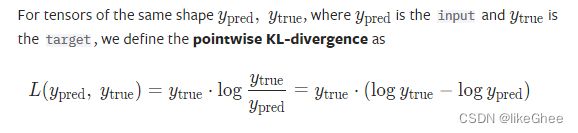
input可以是任意的维度，target和input一样的形状
为防止下溢的问题，input期望是log空间传入进来的，target可以是log空间也可以是线性空间

CE = IE + KL

做机器学习的时候，用CE和kld其实是一样的，因为IE传入的target分布是一个one-hot分布，熵其实为0，如果是非delta分布计算出的结果也是一个常数，对参数更新没有任何贡献

# 验证CE = IE + KL
print("=" * 100)
ce_loss_fn_sample = nn.CrossEntropyLoss(reduction='none')
ce_loss_sample = ce_loss_fn_sample(logits, torch.softmax(target_logits, dim=-1))
print("ce_loss_sample: ", ce_loss_sample)

kl_loss_fn_sample = nn.KLDivLoss(reduction='none')
kld_loss_sample = kl_loss_fn_sample(torch.log(torch.softmax(logits, dim=-1)),
                                    torch.softmax(target_logits, dim=-1)).sum(-1)
print("kld_loss_sample: ", kld_loss_sample)

target_info_entropy = torch.distributions.Categorical(
    probs=torch.softmax(target_logits, dim=-1))\
    .entropy()

print("target_info_entropy:",  target_info_entropy)

print(torch.allclose(ce_loss_sample, target_info_entropy + kld_loss_sample))

BCE loss

二分类loss binary cross entropy
公式相当熟悉了
torch.nn.BCELoss(weight=None, size_average=None, reduce=None, reduction='mean')

yn目标分布，xn是预测分布，BCE Loss的一般形式就是NLL loss

target y在0到1之间，这里输入的input是一个类别的标量

# bce loss
bce_loss_fn = torch.nn.BCELoss()
logits = torch.randn(bs)
prob_1 = torch.sigmoid(logits)
target = torch.randint(2, size=(bs, ))
bce_loss = bce_loss_fn(prob_1, target.float())
print(f"bce: {bce_loss}")

# 用NLL代替BCE
prob_0 = 1 - prob_1.unsqueeze(-1)
# 传入的是完整的概率
prob = torch.cat([prob_0, prob_1.unsqueeze(-1)], dim=-1)
# 传入的是对数的概率，
nll_loss_binary = nll_loss_fn(torch.log(prob), target)
print(nll_loss_binary)

COSINEEMBEDDINGLOSS

torch.nn.CosineEmbeddingLoss(margin=0.0, size_average=None, reduce=None, reduction='mean')

余弦相似度loss 一般是用在自监督学习，对比学习，做相似度匹配

如图片检索，找到top100相似图片，用预训练模型算出每张图片的向量表征，用query图片和每张图片做余弦相似度

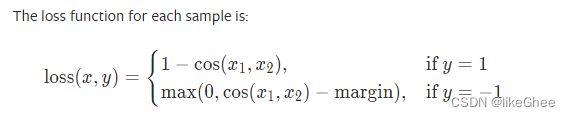
y只能为1或者-1

# Cos Similarity loss
cos_loss_fn = nn.CosineEmbeddingLoss()
v1 = torch.randn(bs, 512)
v2 = torch.randn(bs, 512)
target = torch.randint(2, size=(bs, )) * 2 - 1  # [0，1] * 2 -1 = -1和1
cos_loss = cos_loss_fn(v1, v2, target)
print(f"cos_loss:{cos_loss }")