第六章 算法algorithms

1. 算法概念

1. 以有限的步骤， 解决逻辑或数学上的问题， 这 一专门科目我们称为算法(Algorithms)。
2. 算法与数据结构(Data Structures , 亦即STL中的容器，本书4,5两章巳介绍）。
3. 广义而言，我们所写的每个程序都是一个算法，其中的每个函数也都是一个算法，毕竟它们都用来解决或大或小的逻辑问题或数学问题。
4. 唯有用来解决特定间题（例如排序、查找、最短路径、 三点共线…），并且获得数学上的效能分析与证明， 这样的算法才具有可复用性。
5. 本章探讨的便是被收记录于STL之中，极具复用价值 的70余个STL算法， 包括赫赫有名的排序(sorting)、 查找(searching)、 排列组合(permutation)算法， 以及用于数据移动、 复制、 删除、 比较、 组合、 运算等等的算法。
6. 特定的算法往往搭配特定的数据结构。
7. 例如binary search tree (二叉查找树）和RB-tree(红黑树，5.2节）便是为了解决查找问题而发展出来的特殊数据结构。
8. hashtable(散列表，5.7节）拥有快速查找的能力。
9. 又例如max-heap(或min-heap) 可以协助完成所谓的heapsort (堆排序）。
10. 几乎可以说，特定的数据结构是为了实现某种特定的算法。这一类”与特定数据结构相关＂的算法，被本书（及STL)归 类于第5章“关系型容器"(associated containers)之列。
11. 本章所讨论的，是可施行于“无太多特殊条件限制”之空间中的某一段元素区间的算法。

1.1 算法分析与复杂度表示O()

1. 当发现一个可以解决问题的算法时，下一个重要步骤就是决定该算法所耗用的资源,包括空间和时间。这个操作称为算法分析（algorithm analysis）。
2. 可以这么说，如果一个算法得耗用数GB的内存空间才能获得令人满意的效率，这种算法没有用。（至少在目前的计算机架构下没有实用价值）。
3. 一般而言，算法的执行时间和其所要处理的数据量有关，两者之间存在某种函 数关系，可能是一次（线性，linear)、二次(quadratic)、三次(cubic)或对数(logarithm) 关系。
4. 当数据量很小时，多项式函数的每一项都可能对结果带来相当程度的影响， 但是当数据量够大（这是我们应该关注的情况）时，只有最高次方的项目才具主导地位。

下面是三个复杂各异的问题：

1. 最小元素问题：求取array中的最小元素。：最小元素问题的解法一定必须两两元素比对，逐一进行。N个元素需要N次比 对，所以数据量和执行时间呈线性关系。
2. 最短距离问题：求取X-Y平面上的N个点中，距离最近的两个点。：“最短距离”问题所需计算的元素对(pairs) 共有N(N-1)/2!,所以大数据量和执行时间呈二次关系。
3. 三点共线问题：决定X-Y平面上的N个点中，是否有任何三点共线。："三点共线”问题要计算的元素对(pairs)共有N(N-1)(N-2)/3!, 所以大数据量和执行时间呈三次关系。
   上述三种复杂度， 以所谓的Big-Oh标记法表示为O(N), O(N²), O(N³）。 这种 标记法的定义如下：
   如果有任何正值常数c和N0(0下标）， 使得当N ≥N0（0为下标）时，T(N) ≤ cF(N), 那么我们便可将T(N)的复杂度表示为O(F(N)) 。（注意，在此定义之下，意味着数据量必须足够大，而且最高次方的常系数和较低次方 的项， 都不应该出现在Big-Oh标记法中。）

Big-Oh并非唯一的复杂度标记法， 另外还有诸如Big-Omega, Big-Theta, Little-Oh等标记法， 各有各的优缺点。 一般而言，Big-Oh标记法最被普遍使用。 但是它并不适合用来标记小数据量下的情况。

以下三个问题出现一种新的复杂度形式：

1. 需要多少bits才能表现出N个连续整数？

2. 从X= 1开始， 每次将X扩充两倍， 需要多少次扩充才能使X≥N?

3. 从X=N开始， 每次将X缩减一半， 需要多少次缩减才能使x≤1?

• 就问题1而言，B个bits可表现出2B（B上标）个不同的整数，因此欲表现N个连续整 数， 需满足方程式2B（B上标）≥N, 亦即B≥logN。

  • 问题2称为 ＂持续加倍问题” ， 必须满足方程式2K（K上标） ≥N, 此式同问题1, 因 此解答相同 。
  • 问题3称为 ＂持续减半问题” ，与问题2意义相同， 只不过方向相 反， 因此解答相同。
  • 如果有一个算法，花费固定时间（常数时间，O(1))将问题的规模降低某个固 定比例（通常是1/2), 基于上述问题3的解答，我们便说此算法的复杂度是O(logN)。
  • 注意， 问题规模的降低比例如何， 并不会带来影响， 因为它会反应在对数的底上， 而底对于Big-Oh标记法是没有影响的（任何算法专论书籍， 都应该有其证明）。

1.2 STL算法总览

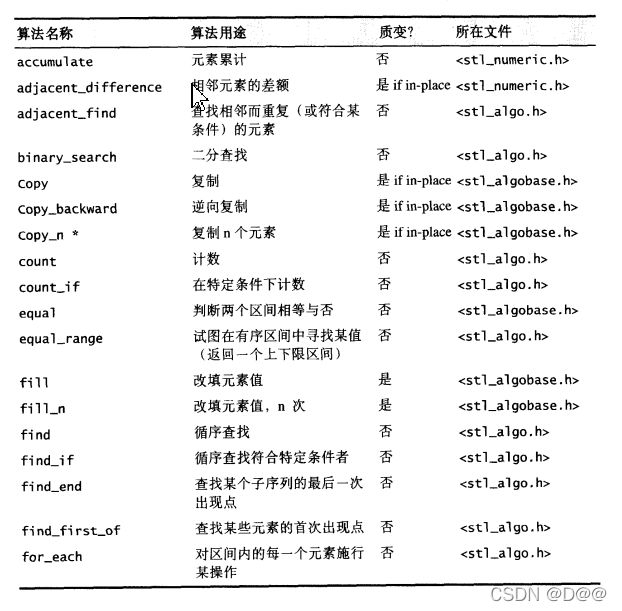
下图将所有的STL算法（以及一些非标准的SGI STL算法）的名称、用途、 文件分布等等，依算法名称的字母顺序列表。表格之中凡是不在STL标准规格之 列的SGI专属算法，都以＊加以标示。
注：（以下 “质变 ” 栏意指mutating, 意思是 “会改变其操作对象之内容,)

1.3 质变算法mutating algorithms(会改变操作对象之值）

1. 所有的STL算法都作用在由迭代器[first,last)所标示出来的区间上。
2. 所 谓“质变算法”，是指运算过程中会更改区间内（迭代器所指）的元素内容。
3. 诸如拷贝(copy)、互换(swap)、替换(replace)、填写(fill)、删除(remove)、 排列组合(permutation)、分割(partition)、随机重排(random shuffling)、排序(sort)等算法，都属此类。如果你将这类算法运用于一个常数区间上，例如

int ia[] = { 22 ,30,30 ,17,33,40,17, 23, 22,12, 20 }; 
vector<int> iv(ia, ia+sizeof(ia)/sizeof(int));
vector<int>::const_iterator cite1 =iv.begin(); 
vector<int>::const_iterator cite2 = iv.end();
sort(cite1,cite2);

针对上述的sort操作，编译器会有错误信息。

1.4 非质变算法nonmutating algorithms(不改变操作对象之值）

1. 所有的STL算法都作用在由迭代器[first,last）所标示出来的区间上。
2. 所谓“非质变算法"，是指运算过程中不会更改区间内（迭代器所指）的元素内容。
3. 诸如查找(find)、匹配(search)、计数(count)、巡访(for_each)、比较(equal,mismatch)、寻找极值(max,min)等算法，都属此类。但是如果你在for_each（巡访每个元素）算法身上应用一个会改变元素内容的仿函数(functor), 例如：

template<class T>
struct plus2{
void operator()(T& x)const
{x +=2;}
};

int ia[] = { 22,30,30,17,33,40,17,23,22,12,20 };
 vector<int>iv(ia, ia+sizeof(ia)/sizeof(int));
for_each(iv.begin(), iv.end(), plus2<int>());

那么当然元素会被改变。

1.5 STL算法的一般形式

1. 所有泛型算法的前两个参数都是一对迭代器(iterators), 通常称为first和last，用以标示算法的操作区间。

2. STL习惯采用前闭后开区间（或称左涵盖区间）表示法，写成［first，last),表示区间涵盖first至last(不含last)之间的 所有元素。

3. 当first==last时，上述所表现的便是一个空区间。

4. 这个[first，last)区间的必要条件是，必须能够经由increment(累加）操作符的反复运用，从first到达last。

5. 编译器本身无法强求这一点。如果这个条件不成立，会导致未可预期的结果。

   根据行进特性，迭代器可分为5类（见3.4.5），每一个STL算法的声明，都表现出它所需的最低程度的迭代器类型。

   1. 例如find()需要一个lnputlterator, 这是它的最低要求， 但它也可以接受更高类型的迭代器， 如Forwardlterator, Bidirectionallterator或RandomAccesslterator , 因为， 由3.4.5图观之， 不论 ForwardIterator或Bidirectionallterator或RandomAccesslterator也都是 一 种 lnputtterator。但如果你交给find() 一个Outputtterator, 会导致错误。
   2. 将无效的迭代器传给某个算法，虽然是一种错误，却不保证能够在编译时期就被捕捉出来，因为所谓 “迭代器类型”并不是真实的型别，它们只是function template 的一种型别参数(type parameters)。

   许多STL算法不只支持一个版本。这一类算法的某个版本采用缺省运算行为，另一个版本提供额外参数，接受外界传入一个仿函数(functor) , 以便采用其他策略。:

   1. 例如unique()缺省情况下使用equality操作符来比较两个相邻元素，但如果这些元素的型别并未供应equality操作符，或如果用户希望定义自己的equality操作符，便可以传一个仿函数(functor)给另一版本的unique()。

   有些算法干脆 将这样的两个版本分为两个不同名称的实体，附从的那个总是以 ＿if作为尾词:

   1. 例如find_if ()。 另 一个例子是replace(), 使用内建的equality操作符进行比对操作，replace_if ()则以接收到的仿函数(functor)进行比对行为。

   质变算法(mutating algorithms）通常提供两个版本：

   1. 一个是in-place（就地进行）版，就地改变其操作对象； 另 一个是copy (另地进行）版，将操作 对象的内容复制一份副本，然后在副本上进行修改并返回该副本。

   2. copy版总是以 _copy作为函数名称尾词，例如replace ()和 replace_copy ()。

   3. 并不是所有质 变算法都有copy版， 例如sort（）就没有。

   4. 如果我们希望以这类 “无copy版本 之质变算法施行于某一段区间元素的副本身上，我们必须自行制作并传递那一份副本。

所有的数值(numeric)算法，包括adjacent_difference(), accumulate(), inner_product () , partial_sum()等等，都实现于SGl之中，这是个内部文件，STL规定用户必须包含的是上层的。其他STL算 法都实现于SGI的和文件中，也都是内部文件；欲使用这些算法，必须先包含上层相关头文件。

2. 算法的泛化过程

1. 将一个叙述完整的算法转化为程序代码，是任何训练有素的程序员胜任愉快的工作。这些工作有的极其简单（例如循序查找），有的稍微复杂（例如快速排序法）， 有的十分繁复（例如红黑树之建立与元素存取），但基本上都不应该形成任何难以跨越的障碍。
2. 如何将算法独立于其所处理的数据结构之外，不受数据结构的羁绊，思想层面就不是那么简单了。
3. 如何设计一个算法， 使它适用于任何（或大多数）数据 结构呢？换个说法， 我们如何在即将处理的未知的数据结构（也许是array, 也许 是vector, 也许是list, 也许是deque… )上， 正确地实现所有操作呢？
4. 关键在于，只要把操作对象的型别加以抽象化，把操作对象的标示法和区间目 标的移动行为抽象化，整个算法也就在 一个抽象层面上工作了。 整个过程称为算法 的泛型化(generalized) , 简称泛化。

项目是个算法泛化的实例，以简单的循序查找为例，假设写个find（）函数，在array中寻找特定值，面对整数array，我们直觉反应是：

int* find(int* arrayHead,int arraySize,int value)
{
for(int i=0;i<arraySize;++i)
if(arrayHead[i] == value)
break;
return &(arrayHead[i]);
}

1. 该函数在某个区间内查找value。返回的是一个指针， 指向它所找到的第一个符合条件的元素；
2. 如果没有找到， 就返回最后一个元素的下一位置（地址）。“最后元素的下一位置” 称为end。
3. 返回 end以表示 “查找无结果” 似乎是个可笑的做法。 为什么不返回null? 稍后即将见到的， end 指针可以 对其他种类的容器带来泛型效果， 这是null所无法达到的。
4. 使用array时千万不要超越其区间，但事实上一个指向array元素的指针， 不但可以合法地指向array内的任何位置， 也可以指向array尾端以外的任何位 置。
5. 只不过当指针指向array尾端以外的位置时， 它只能用来与其他array指针 相比较， 不能提领(dereference)其值。 现在， 你可以这样使用find()函数：

const int arraySize = 7;
int ia[arraySize] = {0,1,2,3,4,5,6};
int* end = ia+arraySize;//最后元素的下一个位置

int* ip = find(ia,sizeof(ia)/sizeof(int),4);
if(ip == end)//两个array指针比较
cout<<"4 not found"<<endl;
else
cout<<"4 found"<<*ip<<endl;

find()的这种做法暴露了容器太多的实现细节（例如arraySize) , 也因此 太过依附特定容器。为了让find()适用于所有类型的容器，其操作应该更抽象化 些。 让find()接受两个指针作为参数， 标示出一个操作区间， 就是很好的做法：

int* find(int* begin,int* end,int value)
{
while(begin !=end && *begin !=value)
++begin;
return begnin;
}

这个函数在“前闭后开”区间[begin,end)内（不含end；end指向array最后元素的下一位置）查找value,并返回一个指针，指向它所找到的第一个符合条件的元素；如果没有找到，就返回end。可以使用find（）函数：

const int  arraySize 7 ;
int ia[arraySize]={0,1,2,3,4,5,6};
int* end = ia+arraySize;

int * ip = find(ia,end,4);
if(ip ==end)
cout<<"4 not found"<<endl;
else
cout<<"4 found"<<*ip<<endl;

find（）函数也可以很方便地用来查找array的子区间：

int* ip =find(ia+2,ia+5,3);
if(ip == end)
cout<<"3 not found"<<endl;
else
cout<<"3 found"<<*ip<<endl;

由于find()函数之内并无任何操作是针对特定的整数array而发的，所以我们可将它改成一个template:

template <typename T>//关键字typename也可改为关键字class
T* find(T* begin,T* end,const T& value)
{
//注意，以下用到operator!=,operator*,operator++
while(begin !=end && *begin !=value)
++begin;
//注意，以下返回操作会引发copy行为
return begin;
}

请注意数值的传递由pass-by-value改为pass-by-reference-to-const , 因为 如今所传递的value, 其型别可为任意；于是对象一大， 传递成本便会提升， 这是 我们不愿见到的。pass-by-reference可完全避免这些成本。
这样的find()很好， 几乎适用于任何容器一一只要该容器允许指针指入， 而指针们又都支持以下四种find()函数中出现的操作行为：

1. inequality (判断不相等）操作符
2. dereferencelm (提领，取值）操作符
3. prefix increment (前置式递增）操作符
4. copy (复制）行为（以便产生函数的返回值）

• C++有一个极大的优点， 几乎所有东西都可以改写为程序员自定义的形式或行为。是的， 上述这些操作符或操作行为都可以被重载(overloaded) , 既是如此，何必将find限制为只能使用指针呢？何不让支持以上四种行为的、行为很 像指针的 ＂某种对象” 都可以被find()使用呢？

  • 如此 一来， find()函数便可以从原生(native)指针的思想框框中跳脱出来。 如果我们以一个原生指针指向某个 list, 则对该指针进行"++ “操作并不能使它指向下一个串行节点。但如果我们设计一个class,拥有原生指针的行为，并使其”++"操作指向list的下一个节点，那么find()就可以施行于list容器身上了。

    • 这便是迭代器(iterator,第三章）的观念。迭代器是一种行为类似指针的对象，换句话说，是一种smart pointerss。现在我将find(）函数内的指针以迭代器取代， 重新写过：

template<class Iterator, class T> 
Iterator find(Iterator begin, Iterator end, const T& value)
{
	while(begin !=end && *begin !=value)
	++begin;
	return begin;
}

这便是一个完全泛型化的find()函数。你可以在任何C++标准库的某个头文件里看到它，长相几乎一模一样。SGI STL把它放在之中。有了这样的观念与准备，再来看STL各式各样的泛型算法，就轻松多了。以 下列出（几乎）所有STL算法的源代码，并列有用途说明与操作示范。

3. 数值算法（stl_numeric.h）

这一节介绍的算法，统称为数值（numeric）算法。STL规定，使用它们客户端必须包含头文件。SGL将它们实现于文件中。

3.1 运用实例

• 观察这些算法的源代码之前，先示范其用法，是个比较好的学习方式。以下程序展示本节所介绍的每一个算法的用途。
  • 例中使用ostream_iterator作为输出工具，第8章会深入介绍它，目前请想象它是个绑定到屏幕的迭代器；
    • 只要将任何型别吻合条件的数据丢往这个迭代器，便会显于屏幕上，而这一迭代器会自动跳到下一个可显示位置。

#include
#include
#include
#include//ostream_iterator
#include
using namespace std;

int main()
{
	int ia[5] = {1,2,3,4,5};
	verctor<int> iv(ia,ia+5);
	cout<<accumulate(iv.begin(),iv.end(),0)<<endl;
	//15,i.e. 0+1+2+4+5
	cout << accumulate(iv.begin() , iv.end(),0, minus<int> ())<< endl; 
	// -15, i.e. O -1 -2 -3 -4 -5 
	cout << inner_product(iv. begin() , iv.end() , iv.begin(),10)<<endl;
	// 65, i.e. 10 + 1*1 + 2*2 + 3*3 + 4*4 + 5*5 
	cout << inner_product(iv.begin(), iv.end(), iv.begin(), 10, 
	minus<int>(), plus<int>()) << endl; 
	// -20, i.e. 10 -1+1 -2+2 -3+3 -4+4 -5+5 
	//以下这个迭代器将绑定到cout,作为输出用
	ostream_iterator<int>oite (cout, " ");
	partial_sum(iv.begin(),iv.end(),oite);
	//1 2 6 10 15(第n个元素是前旧元素的相加统计）
	partial_sum(iv.begin(),iv.end(),oite,minus<int>());
	
	adjacent_difference(iv.begin(),iv.end(),oite);
	// 1 1 1 1 1(#1元素照录，#n新元素等于#n旧元素-#n-1旧元素）
	adjacent_difference(iv.begin(),iv.end(),oite,plus<int>());
	//1 3 5 7 9(#1元素照录，#n新元素等于op(#n旧元素，#n-1旧元素))

	cout<<power(10,3)<<endl;//1000 i.e 10*10*10
	cout<<power(10,3,plus<int>())<<endl;//30 i.e 10+10+10
	
	int n= 3;
	iota(iv.begin(),iv.end(),n);//在指定区间内填入n,n+1,n+2...
	for(int i=0;i<iv.size();++i)
	cout<<iv[i]<<' ';//3 4 5 6 7
	}

3.2 accumulate

//版本1
template<class InputIterator,class T>
T accumulate(InputIterator first,InputIterator last,T init){
for(  ;first !=last;++first)
init = init+*first;//将每个元素值累加到初值init身上
return init;
}
//版本2
template<class InputIterator,class T,class BinaryOperation>
T accumulate(InputIterator first,InputIterator last,Tinit,BinaryOperator binary_op){
for( ; first !=last;++first)
init = binary_op(init,*first);//对每一个元素执行二元操作
return init;
}

1. 算法 accumulate用来计算init和[first,last)内所有元素的总和。 注意， 你一定得提供一个初始值init， 这么做的原因之一是当[first,last)为空区间时仍能获得一个明确定义的值。 如果希望计算[first,last)中所有数值的 总和， 应该将init设为0。
2. 式中的二元操作符不必满足交换律（commutive）和结合律。是的，accumulate的行为顺序有明确的定义：先将init初始化，然后针对 [first.last)区间中的每一个迭代器i,依序执行init= init +*i（第一版本）或init=binary_op(init,*i) (第二版本）。

3.3 adjacent_ dfference

//版本1
template <class InputIterator,class OutputIterator>
OutputIterator adjacent_difference(InputIterator first, InputIterator last,OutPutIterator result){
if(first == last) return result;
*result=*first;//首先记录第一个元素
return _adjacent_difference(first, last,result,value_type(first)); 
//侯捷认为（并经实证），不需像上行那样传递调用，可改用以下写法（整个函数）：
// if (first== last) return result;
// *result= *first; 
// iterator_traits::value_type value= *first; 
// while (++first != last)( //走过整个区间
// ... 以下同__adjacent_difference()的对应内容
//这样的观念和做法，适用于本文件所有函数，以后不在叙述
}

template <class InputIterator, class OutputIterator, class T> 
OutputIterator __adjacent_difference(InputIterator first, InputIterator last,OutputIterator result,T*){
T value = *first;
while(++first !=last){
T tmp = *first;
*++result = tmp-value;//将相邻两元素的差额（后-前）,赋值给目的端
value = tmp;
}
return ++result;
}

//版本2
template <class InputIterator,class OutputIterator,class BinaryOperation> 
OutputIterator adjacent_difference(InputIterator first, InputIterator last,OutputIterator result,BinaryOperation bianry_op){
if(first == last) return result;
*result = *first;//首先记录第一个元素
return __adjacent_difference(first,last,reuslt,value_type(first),binary_op);
}

template<class InputIterator,class OutputIterator,class T,class BinaryOperation>
OutputIterator __adjacent_difference(InputIterator first,InputIterator last,OutputIterator result,T*,BinaryOperation binary_op){
T value = *first;
while(++first !=last){//走过整个区间
T tmp = *first;
*++result = binary_op(tmp,value);//将相邻两元素结果，赋值给目的端
value = tmp;
}
return ++result;
}

算法adjacent_difference用来计算[first,last）中相邻元素的差额。也就是说，它将*first赋值给*result,并针对[first+1,last)内的每个迭代器i,将*i-*(i-1)之值赋值给*(result+(i-first)）。
注意，你可以采用就地(in place)运算方式，也就是令result等于first 。是的，在这种情况下它是一个质变算法(mutating algorithm)。

1. “储存第一元素之值，然后储存后继元素之差值”这种做法很有用，因为这么一来便有足够的信息可以重建输入区间的原始内容。
2. 如果加法与减法的定义一如常规定义，那么adjacent_difference与partial_surn(稍后介绍）互为逆运算。
3. 这意思是，如果对区间值1,2,3,4,5执行adjacent_difference,获得结果为 1,1,1,1,1 再对此结果执行partial_surn,便会获得原始区间值1,2,3,4,5。
4. 第一版本使用operator-来计算差额，第二版本采用外界提供的二元仿函数。 第一个版本针对[first+1,last)中的每个迭代器i,将*i-*(i-1)赋值给 *(result+(i-first))，第二个版本则是将binary_op(*i,* (i-1))的运算结 果赋值给＊(result+(i-first))。

3.4 inner_product

//版本1
template<class InputIterator1,class InputIterator2,class T>
T inner_product(InputIterator1 first1,InputIterator1,last1,InputIterator2 first2,T,init){
//以第一序列之元素个数为据，将两个序列都走一遍
for( ; first1 !=last1;++first1,++first2)
init = init+(*first1 * *first);//执行两个序列的一般内积
return init;
}
//版本2
template <class InputIterator1, class InputIterator2, class T,
class BinaryOperation1, class BinaryOperation2> 
T inner_product(InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, T init, BinaryOperation1 binary_op1,BinaryOperation2 binary_op2){
//以第一序列之元素个数为据，将两个序列都走一遍
for(;first1 !=last1;++first1,++first2)
//以外界提供的仿函数来取代第一版本的operator*和operator+
init = binary_op1(init,binary_op2(*first1,*first2));
return init;
}

1. 算法inner_product能够计算[first1, last1)和[first2, first2 + (last1 - first1))的一般内积(generalized inner product)。
2. 注意， 你一定得提供初值init。 这么做的原因之一是当[first,last)为空时，仍可获得一个明确 定义的结果。
3. 如果你想计算两个vectors的一般内积， 应该将init设为0。
4. 第一个版本会将两个区间的内积结果加上init 。也就是说， 先将结果初始化为init, 然后针对[firstl,last1)的每一个迭代器i，由头至尾依序执行 result = result + (*i)* *(first2+(i-first1))。

第二版本与第一 版本的唯一差异是以外界提供之仿函数来取代operator+ 和operator。就是说，首先将结果初始化为init, 然后针对[firstl, last1) 的每一个迭代器 i， 由头至尾依序执行 result = binary_op1(result, binary_op2(*i, *(first2+(i-first1)))。
式中所用的二元仿函数不必满足交换律(commutative)和结合律(associative)。inner_product所有运算行为的顺序都有明确设定。

3.5 partial_sum

//版本1
template <class InputIterator,class OutputIterator>
OutputIterator partial_sum(InputIterator first,InputIterator last,OutputIterator result){
if(first == last)return result;
*result = *first;
return __partial_sum(first,last,result,value_type(first));
}
template <class InputIterator,class OutputInterator,class T>
OutputIterator __partial_sum(InputIterator first,InputIterator last,OutputIterator result,T*){
T value = *first;
while(++fitst !=last){
value = value+*first;//前n个元素的总和
*result = value;//指定给目的端
}
return ++result;
}

//版本2
template<class InputIterator,class OutputIterator,class BinaryOperation>
OutputIterator partial_sum(InputIterator first,InputIterator last,OutputIterator,Binaryeratorion binary_op){
if(first == last)return result;
*result = *first;
return __partial_sum(first,last,reuslt,value_type(first),binary_op);
}
template <class InputIterator,class OutputIterator,class T, 
class BinaryOperation> 
OutputIterator __partial_sum(InputIterator first,InputIterator last,OutputIterator result,T*,BinaryOperation binary_op(){
T value = *first;
while(++first !=last){
value = binary_op(value,*first);//前n个元素的总计
*++result = value;//指定给目的端
}
return ++reuslt;
}

1. 算法partial_sum用来计算局部总和。它会将*first赋值给*result, 将*(first+1)和*(result+1)的和赋值给*(result+1),依此类推。
2. 注意，result可以等于first,这使我们得以完成就地（in place）计算。在这种情况下它是一个质变算法（mutating algorithm）。
3. 运算中的总和首先初始为*first, 然后赋值给*result。
4. 对于 [first+1,last)中每个迭代器i,从头至尾依序执行sum=sum+*i(第一版本）或sum=binary_op(sum, *i) (第二版本），然后再将sum赋值给*(result +(i -first))。
5. 此式所用之二元仿函数不必满足交换律(commutative)和结合 律(associative)。所有运算行为的顺序都有明确设定。
6. 本算法返回输出区间的最尾端位置：result+(last-first)。

如果加法与减法的定义一如常规定义，那么partial_sum与先前介绍过的adjacent_difference互为逆运算。这里的意思是，如果对区间值1,2,3,4,5执行partial_sum,获得结果为1,3,6,10,15,再对此结果执行adjacent_difference, 便会获得原始区间值1,2,3,4,5。

3.6 power

这个算法由SGI专属，并不在STL标准之列。它用来计算某数的n幕次方。 这里所谓的n幕次是指自己对自已进行某种运算，达n次。运算类型可由外界指定； 如果指定为乘法，那就是乘幕。

//版本1，乘幂
template<class T,class Integer>
inline T power(T x,Integer n){
return power(x,n,multiples<T>());//指定运算型式为乘法
}

//版本二，幕次方。如果指定为乘法运算，则当n>= 0时返回x^n
//注意，"MonoidOperation"必须满足结合(associative)
// 但不需满足交换律(commutative)
template <class T, class Integer, class MonoidOperation> 
T power(T x, Integer n, MonoidOperation op) { 
if(n ==0)
return identity_element(op);//取出“证同元素"identity_element;证同元素见7.3节
else{
while((n & 1) == 0){
n>>=1;
x = op(x,x);
}

T result = x;
n >>=1;
while(n !=0){
x = op(x,x);
if((n & 1) !=0)
reuslt = op(result,x);
n>>=1;
}
return result;
}
}

3.7 itoa
这个算法由SGI专属，并不在STL标准之列。它用来设定某个区间的内容，使其内的每一个元素从指定的value值开始，呈现递增状态。它改变了区间内容，所以是一种质变算法(mutating algorithm)。

//侯捷：iota是什么的缩写？
//函数意义：在[first,last)区间内填入value,value+1, value+2 ... 
template <class ForwardIterator, class T> 
void iota(ForwarIterator first, ForwardIterator last, T value) {
while(first !=last) *frist++ = value++;
}

4.基本算法(stl_algobase)

STL标准规格中并没有区分基本算法或复杂算法，然而SGI却把常用的一些算法定义于之中，其它算法定义于如中。以下列举这些所谓的基本算法。

4.1 运用实例

以下程序展示本节介绍的每一个算法的用途（但不含copy,copy_backward的用法，这两者另有范例程序）。本例使用for_each搭配一个自制的仿函数(functor) display作为输出工具，关于仿函数，第7章会深入介绍它，目前请想象它是一个有着函数行径（也就是说，会被function call操作符调用起来）的东西。至于for_each,将在6.7介绍，目前请想象它是一个可以将整个指定区间遍历一遍的循环：

#include
#include
#include
#include
#include
#include
using namespace std;

template <class T>
struct dispaly{
void operator(){const T& x)const
{cout<<x<<' ';}
};

int main()
{
	int ia[9] = {0,1,2,3,4,5,6,7,8};
	vector<int> iv1(ia,ia+9);
	vector<int> iv2(ia,ia+9);
//{0,1,2,3,4} v.s {0,1,2,3,4,5,6,7,8};
cout<<*(mismatch(iv1.begin(),iv1.end(),iv2.begin()).first);//?
cout<<*(mismatch(iv1.begin(),iv1.end(),iv2.begin()).second);//5

//以上判断两个区间的第一个不匹配点。返回一个由两个迭代器组成的pair，
//其中第一个迭代器指向第一区间的不匹配点，第二个迭代器指向第二区间的不匹配点
//上述写法很危险，应该先判断迭代器是否不等于容器的end(),然后才可以做输出操作

//如果两个序列在［first,last)区间内相等，equal()返回true
//如果第二序列的元素比较多，多出来的元素不予考虑
cout << equal(iv1.begin(), iv1.end(), iv2.begin()); // 1, true 
cout<<equal(iv1.begin(),iv.end(),,&ia[3]);//0,false
//{0,1,2,3,4}不等于{3,4，5,6，7}
cout<<equal(iv1.begin(),iv1.end(),&ia[3],less<int>());//1
//{0,1,2,3,4}小于{3,4,5,6,7}

fill(iv1.begin(),iv1.end(),9);//区间区间内全部填9
for_each(iv1.begin(),iv1.end(),dispaly<int>());//9 9 9 9 9

fill_in(iv1.begin(),3,7);//从迭代器所指位置开始，填3个7
for_each(iv1.begin(),iv1.end(),dispaly<int>());//7 7 7 9 9

vector<int>::iterator ite1 = iv1.begin();//指向7
vector<int>::iterator ite2 =ite1;
advance(ite2,3);//指向9
iter_swap(ite1,ite2);//将两个迭代器所指元素对调
cout<<*ite1<<' '<<*ite2<<endl;//9 7
for_each(iv1.begin(),iv1.end(),dispaly<int>());//9 7 7 7 9

//以下取两值之最大
cout<<max(*ite1,*ite2)<<endl;//9
//以下取两值之最小
cout<<min(*ite1,*ite2)<<endl;//7

//千万不要错写成以下那样。那意思是，取两个迭代器（本身）之大者（或小者），
//然后再打印其所指之值。注意，迭代器本身的大小，对用户没有意义
cout<<*max(ite1,ite2)<<endl;//7
cout<<*min(ite1,ite2)<<endl;//9

//此刻状态,iv1:{9 7 7 7 9},iv2:{0 1 2 3 4 5 6 7 8}
swap(*iv1.begin(),*iv2.begin());//将两数值对调
for_each(iv1.begin(),iv1.end(), display<int>()); //0 7 7 7 9
for_each(iv2. begin(),iv2.end(), display<int>()); //9 1 2 3 4 5 6 7 8

//准备两个字符串数组
struct stra1[]={"Jamie","JJHou","Jason"};
struct stra2[]={"Jamie","JJhou","Jerry"};

cout<<lexicographical_compare(stra1,stra1+2,stra2+2);
//1 (stra1小于stra2)

cout<<lexicographoical_compare(stra1,stra1+2,stra2,stra2+@,greate<string>());
//0 (stra1不大于stra2)
}

4.2 equal,fill,fill_n,iter_swap,lexicogrphical_compare,max,min,mismatch,swap

这一小节列出定义于头文件中的所有算法， copy () , copy _backward ()除外，因为这两个函数复杂许多，在效率方面有诸多 考虑，我把它们安排在另外的小节。

①.equal

如果两个序列在[first,last)区间内相等，equal()返回true。如果第二序列的元素比较多，多出来的元素不予考虑。因此，如果我们希望保证两个序列完全相等，必须先判断其元素个数是否相同：

if(vec1.size() == vec2.size() && equal(vec1.begin(),vec1.end(),vec2.begin());

抑或使用容器所提供的equality操作符，例如vec1==vec2。如果第二序列的元素比第一序列少，这个算法内部进行迭代行为时，会超越序列的尾端，造成不可预测的结果。第一版本缺省采用元素型别所提供的equality操作符来进行大小比较，第二版本允许我们指定防函数pred作为比较依据。

template<class InputIterator1,class InputIterator2>
inline bool equal(InputIterator1 first,InputIterator1 last1,InputIterator2 first){
//以下，将序列一走一遍，序列二亦步亦趋
//如果序列一的元素个数多过序列2的元素个数，就糟糕了
for( ;first1 !=last1;++first1,++first2)
if(*first1 =*first2)//只要对应元素不相等
return false;//就结束并返回false
return true;//至此，全部相等，返回true
}

template<class InputIterator1,class InputIterator2,class BinaryPredicate>
inline bool equal(InputIterator1 first1,InputIterator1 last,InputIterator2 first2,BinaryPredicate binary_pred){
for( ; first1 !=last1;++first1,++first2)
if(!binary_pred(*first1,*fitst2))
return false;
return true;
}

②.fill
将[first,last)内的所有元素改填新值。

template<class ForwardIterator,class T>
void fill(ForwardIterator first,ForwardIterator last,const T& value){
for( ;first !=last;++first)//迭代器走过整个区间
*first = value;//设定新值
}

③.fill_n

将[first,last)内的前n个元素改填新值，返回的迭代器指向被填入的1最后一个元素的下一个位置。

template<class OutputIterator,class Size,class T>
OutputIterator fill_n(OutputIterator first,Size n,const T& value){
for( ;n>0;--n;++first)//经过n个元素
*first = value;
reurn first;
}

如果n超越容器的现有大小，会造成声明结果？例如：

int ia[3] = {0,1,2};
vecctor<int> iv(ia,ia+3);

fill_n(iv.begin(),5,7);

从fill_n的源代码知道，由于每次迭代器进行的是assignment操作，是一种覆写（overwirte）操作，所以一旦操作区间超越了容器大小，就会造成不可预期的结果。解决办法之一是，利用inserter()产生一个具有插入(insert)而非覆写（overwirte）能力的迭代器。insert()可产生一个用来修饰迭代器的配接器（iterator adapter），用法如下：

int ia[3] = {0,1,2};
vector<int> iv(ia,ia+3);//0 1 2
fill_n(inserter(iv,iv.begin()),5,7);//7 7 7 7 7 0 1

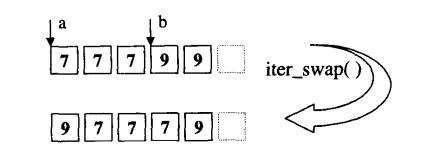
④.iter_swap

将两个ForwardIterators所指的对象对调，如下图：

template <class ForwardIterator1, class ForwardIterator2>
inline void iter_swap(ForwardIterator1 a, ForwardIterator2 b) {
_iter_swap(a, b, value_type(a)); //注意第三参数的型别！
}
template <Class ForwardIiterator1, class ForwardIterator2,class T>
inline void __iter_swap(ForwardIterator a,ForwardIterator2 b,T*){
T tmp = *a;
*a = *b;
*b = tmp;
}

1. iter_swap ()是＂迭代器之value type"派上用场的一个好例子。是的，该函数必须知道迭代器的value type, 才能够据此声明一个对象，用来暂时存放迭代器所指对象。
2. 为此，上述源代码特别设计了一个双层构造，第一层调用第二层，并多出 一个额外的参数value_type(a)。
3. 么一来，第二层就有value type可以用了。乍见之下你可能会对这个额外参数在调用端和接受端的型别感到讶异，调用端是 value_type(a),接受端却是T*。

只要找出value_type()的定义瞧瞧，就一点也不奇怪了：

//以下定义于
template <class Iterator>
inline typename iterator_traits<Iterator>::value_type* 
value_type(const Iterator&) {
return static_cast<typename irterator_traits<Iterator>::value_type*>(0);
} 

这种双层构造在SGI STL源代码中十分普通，其实并非必要，直接这么写：

template<class ForwardIterator1, class ForwardIterator2>
inline void iter_swap(ForwardIterator1 a, ForwardIterator2 b) {
typename iterator_traits<Forwardator1>::value_type 
tmp = *a;
*a = *b;
*b= tmp;
}

⑤.lexicographical_compare

以”字典排列方式”对两个序列[first1,last1)和[first2,last2)进行比较。比较操作针对两序列中的对应位置上的元素进行，并持续直到(1)某一组对 应元素彼此不相等；(2)同时到达last1和last2(当两序列的大小相同）；(3)到达last1或last2(当两序列的大小不同）。

当这个函数在对应位置上发现第一组不相等的元素时，有下列几种可能：

1. 如果第一序列的元素较小，返回true。否则返回false。
2. 如果到达last1而尚未到达last2,返回true。
3. 如果到达last2而尚未到达last1,返回false。
4. 如果同时到达last1和last2(换句话说所有元素都匹配），返回false;

也就是说，第一序列以字典排列方式(lexicographically)而言不小于第二序列。 举个例子，给予以下两个序列：

string stra1 [] = ("Jamie", "JJHou", "Jason" } ;
string stra2 [] = ("Jamie", "JJhou", "Jerry" } ;

这个算法面对第一组元素对，判断其为相等，但面对第二组元素对，判断其为不等。就字符串而言，“JJHou"小于"JJhou”,因为‘H’在字典排列次序上小于 ‘h’ (注意，并非“大写”字母就比较“大”，不信的话看看你的字典。事实卜 大写字母的ASCII码比小写字母的ASCII码小）。于是这个算法在第二组“元素对 "停了下来， 不再比较第三组 “元素对“ 。比较结果是true。

第二版本允许你指定一个仿函数comp作为比较操作之用，取代元素型别所提供的less-than (小于）操作符。

template <class InputIterator1, class InputIterator2> 
bool lexicographical_compare(InputIterator1 first1, InputIterator1 last1,InputIterator2 first2,InputIterator2 last2){
//以下， 任何一个序列到达尾端，就结束。 否则两序列就相应元素一一进行比对 
for ( ;first1 != last1 && first2 != last2; ++first1, ++first2) {
if (*first1< *first2)//第一序列元素值小于第二序列的相应元素值
return true; 
if (*first2 < *first1) //第二序列元素值小于第一序列的相应元素值
return false; 
//如果不符合以上两条件， 表示两值相等， 那就进行下一组相应元素值的比对
}
//进行到这里， 如果第一序列到达尾端而第二序列尚有余额， 那么第一序列小于第二序列 
return first1 == lastl && first2 ! = last2; 
}
ternplate <class InputIterator1, class InputIterator2, class Cornpare> 
bool lexicographical_compare(InputIterator1 first1, InputIteratorl last1,InputIterator2 first2,InputIterator2 last2,Compare comp){
for ( ;first1 !=last1 && first2 !=last2;++first1,++first2){
if(comp(*first1,*first2))
return true;
if(comp(*first2,*first1))
return false;
}
return first1 == last1 && first2 1+last2;
}

为了增进效率，SGI还设计了一个特化版本，用于原生指针const unsigned char*:

inline bool
lexicographical_compare(const usingned char* first1,const usingned char* last1,const usingned char* first2,const usingned char* last2)
{
const size_t len1= last1-first1;//第一序列长度
const size_t len2 = last2-first2; //第二序列长度
//先比较相同长度的一段。memcmp()速度极快
const int result=memcmp(first1,first2,min(len1, len2)); //如果不相上下，则长度较长者被视为比较大
return result != 0? result< 0 : lenl < len2; 
}

其中memcmp()是C标准函数，正是以unsigned char的方式来比较两序列中对应的每一个bytes。除了这个版本，SGI还提供另一个特化版本，用于 原生指针const char*, 形式同上，就不列出其源代码了。

⑥.max

取出两个对象中较大的值，有两个版本，版本一使用对象型别T所提供的greater-than操作符来判断大小，版本二使用仿函数comp来判断大小：

template<class T>
inline const T& max(const T& a,const T& b){
return a<b?b:a;
}

template <class T,class Compare>
inline const T& max(const T& a,const T& b,Compare comp){
return comp(a,b)?b:a;//由comp决定“大小比较”标准
}

⑦.min

取两个对象中的较小值。有两个版本，版本一使用对象型别T所提供的 less-than操作符来判断大小，版本二使用仿函数comp来判断大小。

template <class T> 
inline const T& min(constT& a, const T& b1) {
return b<A?b:a;
}

template <class T,class Compare>
inline const T& min(const T& a,const T& b,Compare comp){
return comp(b,a)?b:a;//由comp决定“大小比较”标准
}

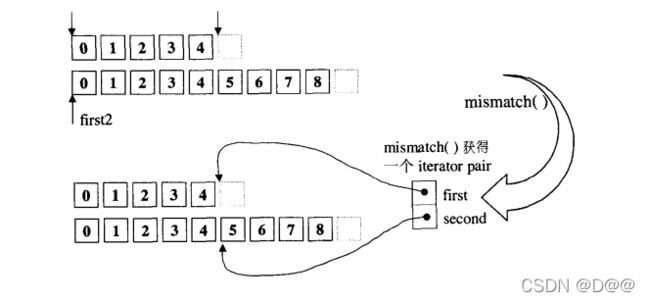
⑧.mismatch

1. 用来平行比较两个序列，指出两者之间的第一个不匹配点。返回 一对迭代器(任何一“对”对象，都可以用pair来表达）,分别指向两序列中的不匹配点， 如下图。
2. 如果两序列的所有对应元素都匹配， 返回 的便是两序列各自的last迭代器。
3. 缺省情况下是以equality操作符来比较元素；但第二版本允许用户指定比较操作。 如果第二序列的元素个数比第一序列多，多出来的元素忽略不计。 如果第二序列的元素个数比第一序列少，会发生未可预期的行 为。

template <class Inputiterator1, class InputIterator2> 
pair<InputIterator1, InputIterator2>mismatch(InputIterator1 first1, InputIterator1 last1,InputIterator2 first2) {
//以下， 如果序列－走完， 就结束
//以下， 如果序列一和序列二的对应元素相等，就结束
//显然， 序列一的元素个数必须多过序列二的元素个数， 否则结果无可预期 
while (first1 != last1 && *first1 == *first2) { 
++first1;
++first2;
}
return pair<InputIterator1,InputIterator2>(first1,first2);
}
template<class InputIterator1,class InputIterator2,class BinaryPredicate>
pair<InputIterator1,InputIterator2>mismatch(
InputIterator1 first1,InputIterator1 last1,InputIterator2 first2,BinaryPredicate binary_pred){
while(first !=last1 && binary_pred(*first1,*first2)){
++first1;
++first2;
}
return pair<InputIterator1,Inputerator2>(first1,first2);
}

⑨.swap

该函数用来交换（对调）两个对象的内容。

template<class T>
inline void swap(T& a,T& b){
 T tmp = a;
 a = b;
 b = tmp;
 }

4.3 copy:强化效率无所不用其极

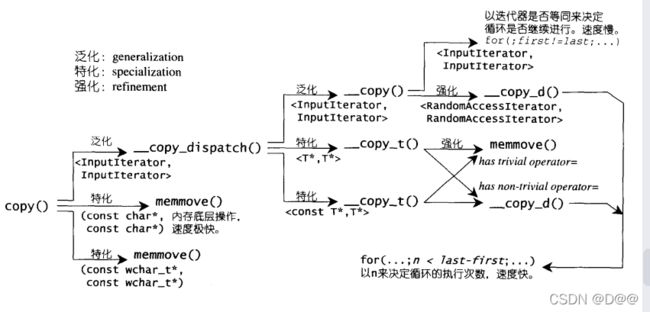
1. 不论是对客端程序或对STL内部而言，copy()都是个常常被调用的函数。
2. 由于copy进行的是复制操作，而复制操作不外乎运用assignment operator或copy constructor (copy算法用的是前者），但是某些元素型别拥有的是trivial assignment operator, 因此，如果能够使用内存直接复制行为（例如C标准函数memmove或memcpy), 便能够节省大量间。
3. 为此，SGI STL的copy算法用尽各种办法，包括函数重载(function overloading)、型别特性(type traits)、偏特化(partial specialization)等编程技巧，无所不用其极地加强效率。下图表示整个copy()操作的脉络。配合稍后出现的源代码，可收目了然之效。

1. copy算法可将输入区间［first,last)内的元素复制到输出区间[result，result+(last－first))。
2. 也就是说，它会执行赋值操作*result= *first,*(result+1) = *(first+1),…依此类推。返回一个迭代器:result+(last-first）。
3. copy对其template参数所要求的条件非常宽松。其输入区间只需由lnputlterators构成即可，输出区间只需由Outputlterator构成即可。
4. 这意味着你可以使用copy算法，将任何容器的任何一段区间的内容，复制到任何容器的任何一段区间上，如下图所示。
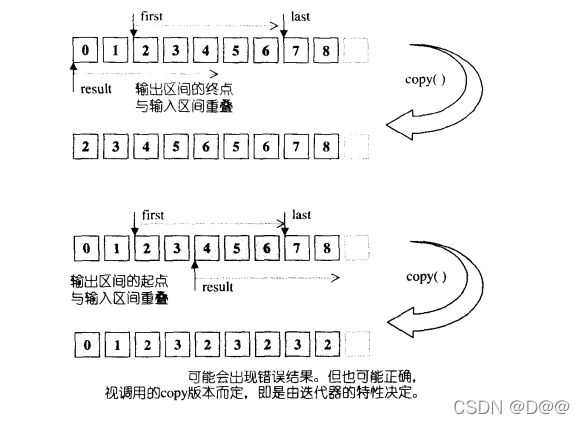
5. 对于每个从0到last-first(不含）的整数n,copy执行赋值操作 * (result+n) = * (first+n)。赋值操作是向前（亦即累加n)推进的。（注：如果输入区间和输出区间重叠，赋值顺序需要多加讨论。 当result位于[first,last)之内时，如果输出区间的起头与输入区间 重叠，我们便不能使用copy。但如果输出区间的尾端与输入区间重叠，就可以使用 copy。copy_backward的限制恰恰相反。如果两个区间完全不重叠，两个算法都可以用。如果result是个ostream_iteraror或其它某种“语意视赋值顺序而定”的迭代器，那么赋值顺序一样会成为一个需要讨论的问题。）

• 如果区间完全没有重叠，当然毫无问题，否则便需特别注意。
  • 为什么上图第二种情况（可能）会产生错误？从稍后即将显示的源代码可知，copy 算法是一一进行元素的赋值操作，如果输出区间的起点位于输入区间内，copy算法便（可能）会在输入区间的（某些）元素尚未被复制之前，就覆盖其值，导致错误结果。
    • 在这里我一再使用“可能“这个字眼，是因为，如果copy算法根据其所接收的迭代器的特性决定调用memmove()来执行任务，就不会造成上述错误，因为memmove()会先将整个输人区间的内容复制下来，没有被覆盖的危险。

测试：

#include
#include
#include//deque拥有RandomAccesslterator
using namespace std;

template<class T>
struct display{
void operator()(const T& x)
{cout<<x<<' ';}
};

int main()
{
int ia[] = {0,1,2,3,4,5,6,7,8};
//以下，输出区间的终点与输入区间重叠，没问题
copy(ia+2,ia+7,ia);
for_each(ia,ia+9,dispaly<int>());//2 3 4 5 6 7 8
cout<<endl;
}
{
int ia[] = {0,1,2,3,4,5,6,7,8};
//以下，输出区间的起点与输入区间重叠，可能会有问题
copy(ia+2,ia+7,ia+4);
for_each(ia,ia+9,display<int>());// 0 1 2 3 2 3 4 5 6
cout<<endl;
//本例结果正确，因为调用的copy算法使用memmove()执行实际复制操作
}

{
int ia[] ={0,1,2,3,4,5,6,7,8};
deque<int>(ia,ia+9);
deque<int>::iterator first = id.begin();
deque<int>::iterator last = id.end();
++++first;//advance(first,3);
cout<<*first<<endl;//2
----last;//advance(last,-2);
cout<<*last<<endl;//7

deque<int>::iterator result = id.begin();
cout<<*result<<endl;//0

//以下，输出区间的终点与区间重叠，没有问题
copy(first,last,result);
for_each(id.begin(),id.end(),display<int>());//2 3 4 5 6 7 8
cout<<endl;
}

{
int ia [] = { 0, 1, 2, 3, 4, 5, 6, 7, 8}; 
deque<int> id(ia, ia+9); 

deque<int>::iterator firsL = id.begin();
deque<int>::iteratorlast = id.end();
  ++++first; //advance(first,2);
cout << *first<<endl; //2
----last;//advance (last,-2);
cout<<*last<<endl;//7

deque<int>::iterator result = id.begin();
advance(result,4);
cout<<*result<<endl;//4
//以下，输出区间的起点与输入区间重叠，可能会有问题
copy(first, last, result); 
for_each(id.begin(), id.end(), display<int>()); // O 1 2 3 2 3 2 3 2 
cout << endl; 
//本例结果错误，因为调用的copy算法不再使用memrnove()执行实际复制操作
}
}

1. 请注意，如果以vector取代上述的deque进行测试，复制结果将是正确 的，因为vector迭代器其实是个原生指针(nativepointer) , 见4.2.3节，导致调 用的copy算法以memmove()执行实际复制操作。
2. copy更改的是[result,result+(last-first))中的迭代器所指对象，而非更改迭代器本身。它会为输出区间内的元素赋予新值，而不是产生新的元素。它 不能改变输出区间的迭代器个数。换句话说，copy不能直接用来将元素插入空容 器中。
3. 如果想要将元素插入（而非赋值）序列之内，要么明白使用序列容器的insert成员函数，要么使用copy算法并搭配insert_iterator(8.3.1节）。

了解copy算法的实现细节，也是唯一的对外接口：

//完全泛化版本
template <class InputIterator, class OutputIterator>
inline OUtputIterator oapy(InputIterator first, InputIterator last,OutputIterator result)
{
return __copy_dispatch<InputIterator,OutputIterator>()
		(first,last,result);
		}

下面两个是多载函数，针对原生指针（可视为一种特殊的迭代器）const char和const wchar_t，进行内存直接拷贝操作：

//特殊版本(1)。重载形式
inline char* copy(const char* first, const char* last, char* result)(
memmove(result, first, last -first); 
return result+ (last -first);
} 
//特殊版本(2)。重载形式
inline wchar_t* copy(const wchar_t* first, const wchar_t* last,wchar_t* result) { 
memmove(result, first, sizeof(wchar_t) * (last -first)); 
return result + (last -first); 
}

copy()函数的泛化版本中调用了一个__copy_dispatch()函数,此函数有一个完全泛化版本和两个偏特化版本：

//完全泛化版本
template <class InputIterator,class OutputIterator> 
struct _copy_dispatch 
{
OutputIterator operator()(InputIterator firsT,InputIterator last,OutputIterator result) { 
return _copy(first, last, result, iterator_category(first));
}
};

//偏特化版本(1),两个参数都是T*指针形式
template<class T> 
struct _copy_dispatch<T*, T*> 
{
 T* operator() (T* first, T* last, T* result) {
 typedef typename_type_traits<T>::has_trivial_assignment_operator t;
  return __copy_t(first,last,result,t()); 
  }
  };
//偏特化版本(2)'第一个参数为const T*指针形式，第二参数为T*指针形式 
template<class T> 
struct _copy_dispatch<const T*, T*> 
{
T* operator() (const T* first, const T* last, T* result) {
typedef typename _type_traits<T>::has_trivial_assignment_operator t;
return_copy_t(first,last,result, t()); 
}
}

这里必须兵分两路来探讨。首先，_copy_dispatch()的完全泛化版根据迭代器种类的不同，调用了不同的_copy(),为的是不同种类的迭代器所使用的循环条件不同， 有快慢之别。

// InputIterator版本
template<class InputIterator,class OutputIterator>
inline OutputIterator
 _copy(InputIterator first, InputIterator last,OutputIterator result, input_iterator_tag)
{
//以迭代器等同与否， 决定循环是否继续。 速度慢
for (; first != last; ++result, ++first) 
*result = *first; // assigrunent operator return result; 
}
// RandomAccessiterator版本
template <class RandomAccessIterator, class OutputIterator> 
inline OutputIterator
__copy(RandomAccessIterator first, RandomAccessIterator last,OutputIterator result, random_access_iterator_tag) 
{
//又划分出一个函数， 为的是其它地方也可能用到
return _copy_d(first, last, result, distance_type(first));
}
template <class RandomAccessIterator, class OutputIterator, class Distance> 
inline OutputIterator
__copy_d(RandomAccessIterator first, RandomAccessIterator last, OutputIterator result, Distance*)
{
//以n决定循环的执行次数。 速度快
for (Distance n = last - first; n > O; --n, ++result, ++first) 
*result = *first; //assignment operator 
return result;
}

1. 这是__copy_dispatch ()完全泛化版的故事。 现在回到前述兵分两路之处，
   看看它的两个偏特化版本。 这两个偏特化版是在 “参数为原生指针形式” 的前提下，希望进一步探测"指针所指之物是否具有trivial assignment operator (平凡赋值操作符)＂。
2. 这一点对效率的影响不小，因为这里的复制操作是由assignment 操作符负责，如果指针所指对象拥有non-trivial assignment operator, 复制操作就 一定得通过它来进行。但如果指针所指对象拥有的是trivial assignment operator, 复制操作可以不通过它，直接以最快速的内存对拷方式(memmove())完成。
3. C++语言本身无法让你侦测某个对象的型别是否具有trivial assignment operator, 但是SGI STL采用所谓的__type_traits<>编程技巧来弥补（见3.3.7节）。

通过“增加一层间接性”的手法,得以区分两个不同的__copy_t():

//以下版本适用于“指针所指之对象具备trivial assignment operator" 
template<class T> 
inline T* _copy_t(constT* first, const T* last,T* result,__true_type){
memmove(result, first, sizeof(T) * (last -first));
return result+ (last -first); 
}

//以下版本适用于”指针所指之对象具备non-trivial assignment operator" 
template <class T> 
inline T* __copy_t(const T* first, const T* last, T* result,__false_type){
//原生指针毕竟是一种RandornAccessIterator,所以交给＿copy_d()完成 
return _copy_d(first, last, result, (ptrdiff_t*)0); 
}

以上就是copy()的故事。一个无所不用其极地强化执行效率的故事。

现在做个测试，传给copy()各种不同形式的迭代器，看看它会调用 哪个（或哪些）函数。首先，这得修改SGI STL源代码，才能在函数被调用时输出函数名称。修改源代码是件冒险的工作,对已经摸熟SGI STL源代码的，修改它不是不可能的任务。但务必先做万全准备，将备份起来，以便日后回复原状。接下来，在上述每一个copy相关函数中输出一个字符串，代表函数名称。

#include // for cout
#include  // for copy() 
#include  
#include  
#include  
#include "6string" // class String ,by J.J.Hou
using namespace std; 
class C 
{
public: 
C(): _data(3) { }
// 简单的赋值操作符
private:
int _data;
};

int main()
{
//测试1
const char ccs[5]={'a','b','c','d','e'};//数据来源
char ccd[5];//数据去处
copy(ccs,ccs+5,ccd);
//调用的版本是copy(const,char*)

//测试2
const wchar_t cwcs[5] = {'a','b','c','d','e'};//数据来源
wchar_t cwcd[5];//数据去处
copy(cwcs, cwcs+S, cwcd); 
//调用的版本是copy(const wchar_t*) 

//测试3
int ia[5] = (0,1,2,3,4}; 
copy(ia, ia+5, ia);//注意， 数据来源和数据去处相同。 这是允许的
 //调用的版本是
// copy () 
//__copy_dispatch(T*,T*)
//__copy_t(__true_type)

//测试4
//注：list迭代器被归类为InputIterator
list<int> ilists(ia, ia+5); //数据来源
list<int> ilistd(5); //数据去处
copy(ilists.begin(), ilists.end(), ilistd.begin());
//调用的版本是
// copy() 
// copy_dispatch() 
// _copy(input_iterator)

//测试5
//注:vector迭代器被归类为原生指针(native pointer)
vector<int>ivecs(ia, ia+5);//数据来源
//以上会产生输出信息， 原因见稍后正文说明。 此处对输出信息暂略不显
vector<int> ivecd(5); //数据去处
copy(ivecs.begin(), ivecs.end(), ivecd.begin());
//copy()
//__copy_dispatch(T*,T*)
//__copy_t(__true_type)
//
//以上是合理的吗？难道不该是这样吗？
//copy()
//__copy_dispatch()
//__copy(random_access_iterator)
//__copy_d()
//见稍后正文探讨

//测试6
// class C 具备 trivial operator= 
C c[5]; 
vector<C> Cvs(c, c+5); //数据来源
//以上会产生输出信息，原因见稍后正文说明。此处对输出信息暂略不显
vector<C> Cvd(5);//数据去处
copy(Cvs.begrn(), Cvs.end(), Cvd.begin()); 
//copy () 
//__copy_dispatch(T*,T*) 这合理吗？不是random_access_iterator吗？
//__copy_t(_false_type) 这合理吗？不该是＿true_type吗？
//__copy_d()

//测试7
//注：deque迭代器被归类为randomaccess iterator
deque<C> Cds(c, c+5); //数据来源
deque<C> Cdd(5); //数据去处
copy(Cds.begin(), eds.end(), Cdd.begin()); 
// copy () 
//__copy_dispatch()
//__copy_(random_access_iterator)
//__copy_d()

//测试8
//注:class String定义于"6string.h"内，拥有non-trivial operator= 
//其源代码并未列于书中
vector<String> strvs(5); //数据来源
vector<String> strvd(5);//数据去处
strvs[0] = "jjhou";
strvs[1] = "grace";
strvs[2] = "david";
strvs[3] = "jason";
strvs[4] = "jerry";
copy(strvs.begin(),strvs.end(), strvd.begin()); 
// copy () 
//__copy_dispatch(T*,T*) 这合理吗？不是random_access_iterator吗？
//__copy_(_false_type) 合理，String确实是_false_type
//__copy_d()

//测试9
//注：deque迭代器被归类为randomaccess iterator 
deque<String> strds(5); //数据来源
deque<String> strdd(5); //数据去处
strds.push_back ("jjhou") ; 
strds.push_back("grace"); 
strds.push_back ("david") ; 
strds.push_back ("jason") ; 
strds.push_back ("jerry") ; 
copy (strds.begin() , strds.end(), strdd.begin());
// copy () 
//__copy_dispatch()
//__copy(random_access_iterator)
//__copy_d()
}

以上的执行结果想必引起数个疑惑：

1. 测试5一开始的constructor为什么会制造输出信息？
2. 测试6一开始的constructor为什么也会制造输出信息？
3. 测试5,6, 8 完成copy()操作后，为什么不是走random access iterator的方向，而是走T* 的方向？
4. 测试6的元素型别具有trivial operator=,为何却走__fase_type方向？

前两个问题的解答是一样的:它们所调用的 vector ctor调用copy():

//测试5
vector<int> ivecs(ia, ia+S);
//以下是输出信息
// copy () 
// _copy _dispatch(T*, T*) 
// _copy_t(_true_type) 
// 
//说明：构造一个vector却产生上述三行输出。追踪vector ctor, 我们发现：
// vector::vector(first, last) 
// -> vector::range_initialize(first, last, forward_iterator_tag),
//->vector::allocate_and_copy(n,first,last)
//->::uninitialized_copy(first,last,result)
//->::__uninitialized_copy(first,last,result,value_type(result))
//->::__uninitialized_copy_aux(first,last,result,is_POD())
//->::copy(first,last,result)

第三个问题的解答是：我们以为vector 的迭代器是randomaccess iterator, 没想到它事实上是个T*.这虽然令人错愕，但如果你对4.2.3节还有点印象，至少 不会错愕到跌下马来。4.2.3节的vector定义如下：

tempalte<class T,class Alloc=alloc>//使用缺省alloc为配置器
class vector{
public:
typedef T value_type;
typedef value_type* iterator;//vector的迭代器是原生指针
...
}

是的，vector迭代器其实是原生指针。这就怪不得copy()一旦面对vector迭代器，就往T*的方向走去了。

最后 一个问题是，既然class C具备了trivial operator=, 为什么它被判断为一个_false_type呢？

1. 因为编译器之中，有能力验证 “用户自定义型别”之型 别特性者极少(Silicon Graphics N32或 N64编译器就可以）， 内只针对C++的标量型别(scalar types)做了型别特性记录（见 3.3.7节）。
2. 因此程序中所有的用户自定义型别， 都被编译器视为拥有non-trivial ctor/dtor/operator=。 如果我们确知某个 class 具备的是trivial ctor/dtor/operator=, 例如本例的class c, 我们就得自己动手为它做特性设定， 才 能保证编译器知道它的身份。

要自己动手为某个型别做特性设定， 可借用 (见3.3.7节） 中的__type_traits, 针对class C做 一个特化版本如下：

//编译器无力判别class C的特性("traits"), 我们自己来设定．
//当编译器支持partial specialization, _STL_TEMPLATE_NULL被定义为 
//template<>见
_STL_TEMPLATE_NULL struct _type_traits<C> { 
typedef _false_type	has_tri vial_defaul t_constructor;
typedef _true_type	has_trivial_copy_constructor;
typedef _true_type	has_trival_assignment_operator;
typedef _true_type	has_tri vial_destructor;
typedef _false_type	is_POD_type;
//以上每一个定义都必须完成
};

加上这样的设定之后， 测试6的copy()操作的输出信息为：

// copy (} 
// _copy_dispatch(T*, T*} 合理，因为vector的迭代器是原生指针
// copy_t(_true_type) 编译器现在知道了，class C是 __true_type

4.4 copy_backward

ternplate<class BidirectionalIterator1,class BidirectionalIterator2> 
inline BidirectionalIterator2 copy_backward(BidirectionalIterator1 frst,BidirectionalIterator1 last, BidirectionalIterator2 result);

1. 这个算法的考虑以及实现上的技巧与copy()十分类似，源代码就不列出了。
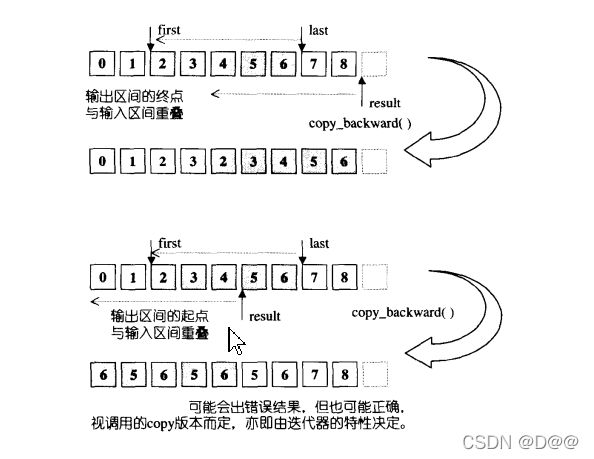
2. 其操作示意于下图所示,将[first,last)区间内的每一个元素，以逆行的方向复制到 以result-1为起点，方向亦为逆行的区间上。
3. 换句话说，copy_backward算法会执行赋值操作*(result-1)=*(last-1),*(result-2) = *(last-2),…依此类推返回一个迭代器：result-(last-first）。copy_backward所接受的迭代器必须是BidirectionIterators才能够“倒行逆施”。
4. 可以使用copy_backward算法，将任何容器的任何一段区间的内容，复制到任何容器的任何一段区间上。如果输 人区间和输出区间完全没有重叠，当然毫无问题，否则便需特别注意，如下图。

测试：

#include
#include
#include//deque拥有RandomAccesslterator
using namespace std;

template <class T>
struct display{
void operator()(const T& x)
{cout<<x<<' ';}
};

int main()
{
{
int ia [] = { 0, 1, 2, 3, 4, 5, 6, 7, 8 }; 
//以下，输出区间的终点与输入区间重叠，没问题 
copy_backward(ia+2, ia+ 7, ia+9); 
for_each(ia, ia+9, display<int>()); 
cout << endl; 
}
{ 
int ia [] = { O, 1, 2, 3, 4, 5, 6, 7, 8 }; 
//以下，输出区间的起点与输入区间重叠，可能会有问题
copy_backward(ia+2, ia+7, ia+5); 
for_each(ia, ia+9, display<int>());// 2 3 4 5 6 5 6 7 8 
cout << endl; 
//本例结果正确，因为调用的copy算法使用memmove()执行实际复制操作
int ia [] = { 0, 1, 2, 3, 4, 5, 6, 7, 8}; 
deque<int> id(ia, ia+9); 

deque<int>::iterator first = id.begin();
deque<int>::iterator last = id.end();
++++first;//advance(first,2);
cout<<*first<<endl;//2
----last;//advance(last,-2);
cout<<*last<<endl;//7
deque<int>::iterator result = id.end();

//以下，输出区间的终点与输入区间重叠，没问题
copy_backward(first,last,result);
for_each(id.begin(), id.end(), display<int>());// O 1 2 3 2 3 4 5 6
cout<<endl;
}
{
int ia[]= {0,1,2,3,4,5,6,7,8};
deque<int> id(ia,ia+9);
deque<int>::iterator first = id.begin();
deque<int>::iterator last = id.end();
++++first;//advance(first,2);
cout<<*first<<endl;//2
----last;//advance(last,-2);
cout<<*last<<endl;//7

deque<int>::iterator result = id.begin();
advance(result,5);
cout<<*result<<endl;//5

//以下， 输出区间的起点与输入区间重叠， 可能会有问题
copy_backward(first, last, result); 
for_each(id.begin(), id.end(), display<int>{)); // 6 5 6.5 6 5 6 7 8 cout << endl; 
//本例结果错误 因为调用的copy算法不再使用memmove()执行实际复制操作
}
}

5. Set相关算法

STL 一共提供了四种与set（集合）相关的算法，分别是并集（unjon）、交集（intersection）、差集（difference）、对称差集（symmetric difference）。

1. 所谓set, 可细分为数学上的定义和STL的定义两种，数学上的set允许元素 重复而未经排序， 例如{1,1,4,6,3 } , STL的定义（也就是set容器， 见5.5.3节） 则要求元素不得重复， 并且经过排序， 例如{1,3,4,6}。
2. 本节的四个算法所接受的 set, 必须是有序区间(sorted range) , 元素值得重复出现。 换句话说，它们可以接 受STL的set /multiset容器作为输人区间。
3. SGI STL另外提供有hash_set/ hash_multiset两种容器，以hashtable 为底层机制（见5.5.8节、5.5.10节），其内的元素并未呈现排序状态，所以虽然名称 之中也有set字样，却不可以应用千本节的四个算法。

• 本节四个算法都至少有四个参数，分别表现两个set区间。以下所有说明都以S1代表第一区间［first1,last1),以S2代表第二区间［first2,last2)。
  • 每一个set算法都提供两个版本（但稍后展示的源代码只列出第一版本），第二版本 允许用户指定"a< b"的意义，因为这些算法判断两个元素是否相等的依据，完全靠“小于“运算。是的，知道何谓“小于“，就可以推导出何谓“等于”。

以下程序测试四个set相关算法。欲使用它们，必须包含。

#include // multiset 
#include  
#include  
#include  // ostream_iterator
using namespace std; 
template <class T> 
struct display{ 
void operator()(const T& x)
{cout<<x<<' ';}
};

int main()
{
int ia1[6] = {1,3,5,7,9,11};
int ia2[7] = {1,1,2,3,5,8,13};

multiset<int> S1(ia1. ia1+6);
multiset<int> S2(ia2, ia2+7);
for_each(S1.begin(), S1.end(), display<int>());
 cout << endl; 
for_each(S2.begin(), S2.end(), display<int>{));
 cout<<endl; 

multiset<int>::iterator first1 =S1.begin();
multiset<int>::iterator last1 =S1.end();
multiset<int>::iterator first2 =S2.begin();
multiset<int>::iterator last2 =S2.end();

cout << "Union of Sl and S2: "; 
set_union(first1, last1, first2, last2,ostream_iterator<int>(cout," "));
cout<<endl;

first1 = S1.begin();
first2 = S2.begin();
cout<<"Intersection of S1 and S2:";
set_intersection(first1,last1,first2,last2,ostream_iterator<int>(cout," "));
cout<<endl;
first1 = S1.begin();
first2 = S2.begin();
cout<<"Difference of S1 and S2 (S1-S2):";
set_difference(first1,last1,first2,last2,ostream_iterator<int>(cout," "));
cout<<endl;
first1 = S1.begin();
first2 = S2.begin();
cout<<"Symmetric difference of S1 and S2:";
set_symmetric_difference(first1,last1,first2,last2,ostream_iterator<int>(cout," "));
cout<<endl;
first1 = S1.begin();
first2 = S2.begin();
last1 = S2.end();
last2 = S1.end();
cout<<"Difference of S2 and S1(S2-S1):";
set_difference(first1,last1,first2,last2,ostream_iterator<int>(cout," "));
cout<<endl;
}

执行结果：

请注意，当集合(set)允许重复元素的存在时，并集、交集、差集、对称差 集的定义，都与直观定义有些微的不同。例如上述的并集结果，我们会直观以为是{1,2,3,5, 7,8,9, 11, 13}, 而上述的对称差集结果，我们会直观以为是{2,7, 8, 9, 11, 13}, 这都是未考虑重复元素的结果。以下各小节对此会有详细说明。

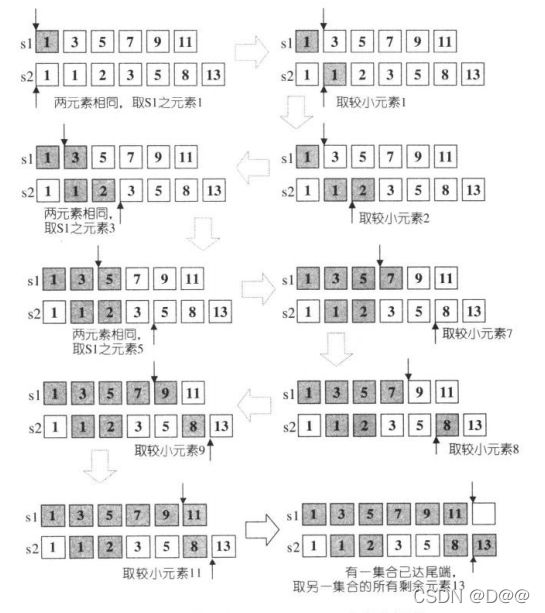
5.1 set_union

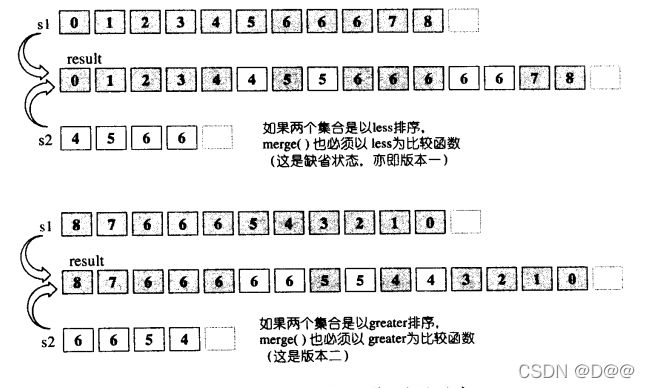
1. 算法set_union可构造S1、S2之并集。也就是说，它能构造出集合S1U S2, 此集合内含S1或S2内的每一个元素。S1、S2及其并集都是以排序区间表示。返回值为一个迭代器，指向输出区间的尾端。
2. 由于S1和S2内的每个元素都不需唯一，因此，如果某个值在S1出现n 次，在S2出现m次，那么该值在输出区间中会出现max(m,n)次，其中n个来自S1,其余来自S2。在STLset容器内，m≦ 1且n≦ 1。
3. set_union是一种稳定(stable)操作，意思是输入区间内的每个元素的相对顺序都不会改变。set_union有两个版本，差别在于如何定义某个元素小于另一 个元素。第一版本使用operator<进行比较，第二版本采用仿函数comp进行比 较。

//并集，求存在于[first1,last1)或存在于[first2,last2)的所有元素
//注意，set是一种sorted range。这是以下算法的前提
//版本一
template <class InputIterator1, class InputIterator2, class OutputIterator>
 OutputIterator set_uuion(InputIterator1 first1, InputIterator1 last1,InputIterator2 first2,InputIterator last2,OutputIterator result){
//当两个区间都尚未到达尾端时，执行以下操作...
while(first1 !=last1 && first2 !=last){
//在两区间内分别移动迭代器口首先将元素值较小者（假设为A区）记录于目标区，
//然后移动A区迭代器使之前进;同时间之另一区迭代器不动。然后进行新一次
//的比大小、记录小值、迭代器移动...直到两区间有一区到达尾端。如果元素相等，
//取S1者记录于目标区，并同时移动两个迭代器
if(*first1 < *first2){
*result = *first1;
++*first1;
}
else if(*first2 < *first1){
*result = *first2;
++*first2;
}
else{//*first2 == *first1
*result = *first1;
++first1;
++first2;
}
++result;
}
//只要两区之中有一 区到达尾端， 就结束上述的while循环
//以下将尚未到达尾端的区间的所有剩余元素拷贝到目的端
//此刻的[first1,last1)和[first2,last2)之中有一个是空白区间 
return copy(first2, last2,copy(first1, last1, result)); 
}

set_union之进行逻辑已经在源代码说明得十分清楚。下图所示的是其一步一步的分析：

5.2 set_intersection

1. 算法set_intersection可构造S1、S2之交集。也就是，它能构造出集合S1∩S2，此集合内含同时出现于S1和S2内的每一个元素。S1、S2及其交集都是以排序区间表示。返回值为一个迭代器、指向输出区间的尾端。
2. 由于S1和S2内的每个元素都不需唯一因此，如果某个值在S1出现n次，在S2出现m次，那么该值在输出区间中会出现min(m, n)次，并且全部来自S1。在STL set容器内，m≤1且m≤1。
3. set_intersection是一种稳定(stable)操作，意思是输出区间内的每个元 素的相对顺序都和S1内的相对顺序相同。它有两个版本，差别在于如何定义某个 元素小于另一个元素。第一版本使用operator<进行比较，第二版本采用仿函数 comp进行比较。

//交集，求存在于[first1,last1)且存在于[first2,last2)的所有元素 
//注意，set是一种sorted range。这是以下算法的前提
//版本一
template <class InputIterator1, class Inputiterator2,class OutputIterator>
 OutputIterator set_intersection(InputIterator1 first1, InputIterator1 last1, InputIterator2 first2,InputIterator2 last2,OutputIterator result){

//当两个区间都尚未到达尾端时，执行以下操作…
while (first1 != last1 && first2 != last2)
//在两区间内分别移动迭代器，直到遇有元素值相同，暂停，将该值记录千目标区，
//再继续移动迭代器...直到两区之中有一区到达尾端
if(*first1< *first2)
++first1;
else if(*first2 < *first1) 
++first2; 
else { // *first2 == *first1
*result = *first1;
++first1;
++first2;
++result;
}
return result;
} 

set_intersection之进行逻辑已经在源代码注释中说明得十分清楚。下图所示的是其一步一步的分析图解。

5.3 set_difference

1. 算法set_difference可构造S1、S2之差集。也就是，它能构造出集合S1-S2，此集合内包含“出现于S1但不出现于S2”的每一个元素。S1、S2及其交集都是以排序区间表示。返回值为一个迭代器，指向输出区间的尾端。
2. 由于S1和S2内的每个元素都不需唯一，因此如果某个值在S1出现n次，在S2出现m次，那么该值在输出区间中会出现max(n-m, 0) 次，并且全部来自S1。在STLset容器内，m≤1且n≤1。
3. set_difference是一种稳定（stable）操作，意思是输出区间的内的每个元素的相对顺序都和S1内的相对顺序相同。它有两个版本，差别在于如何定义某个元素小于另一个元素。第一版本使用operator<进行比较，第二版本采用仿函数comp进行比较。

//差集，求存在于[first1,last1)且不存在于[first2,last2)的所有元素

//注意，set是一种sorted range。这是以下算法的前提
//版本一
template<class InputIterator1, class InputIterator2, class OutputIterator>
OutputIerator set_difference(InputIterator1 first1,InputIterator last1,InputIterator2 first2,InputIterator2 last2,OutputIterator result){
//当两个区间都尚未到达尾端时，执行以下操作...
while (first1 != last1&& first2 != last2)
//在两区间内分别移动迭代器，当第一区间的元素等于第二区间（表示此值同时存在于两区间）
//就让两区间同时进行;当第一区间元素大于第二区间的元素
//就让第二区间前进;有了这两种处理，就保证当第一区间的元素小于第二区间的
//元素时，第一区间的元素只存在第一区间中，不存在于第二区间，于是将它
//记录于目标区
if(*first1<*first2){
*result = *first1;
++first1;
++result;
}
else if(*first2 < *first1)
++first2;
else{//*first2 == *first1
++first1;
++first2;
}
return copy(first1,last1,result);
}

set_difference之进行逻辑已经在源代码注释中说明得十分清楚。下图所示是一步一步的分析：

5.4 set_symmetric_difference

1. 算法set_symmetric_difference可构造S1、S2之对称差集。也就是说，它能构造出集合(S1-S2)U (S2-S1), 此集合内含“出现于S1但不出现于S2"以及“出现于S2但不出现于s1"的每个元素。S1、S2及其交集都是以排序区间。返回值为一个迭代器，指向输出区间的尾端。
2. 由于S1和S2内的每个元素都不需唯一，因此如果某个值在S1出现n次， 在S2出现m次，那么该值在输出区间中会出现In-ml次。如果n>m, 输出 区间内的最后n-m个元素将由S1复制而来，如果n
3. set_ symmetric_difference是一种稳定(stable)操作，意思是输入区间 内的元素相对顺序不会被改变。它有两个版本，差别在于如何定义某个元素小于另 一个元素。第一版本使用operator<进行比较，第二版本采用仿函数comp。

//对称差集，求存在于[first1, last1)且不存在于[first2,last2)的所有元素，
//以及存在于[first2,last2)且不存在于[first1,last1)的所有元索
//注意，上述定义只有在“元素值独一无二的情况下才成立。如果将set一般化，
//允许出现重复元素，那么set-symmetric-difference的定义应该是：
//如果某值在[first1, last1)出现n次，在[first2,last2)出现m次，
//那么它在result range中应该出现abs(n-m)次
//注意，set是一种sorted range。这是以下算法的前提
//版本1
template <class InputIterator1, class InputIterator2, class OutputIterator>
OutputIterator set_symmetric_difference(InputIterator1,first1,InputIterator1 last1,InputIterator2 first2,InputIterator last2,OuputIteraotr result){
//当两个区间都尚未到达尾端时，执行以下操作...
while (first1 != last1 && first2 != last2)
//在两区间内分别移动迭代器。当两区间内的元素相等，就让两区同时前进;
//当两区间内的元素不等，就记录较小值于目标区，并令较小值所在区间前进
if(*first1 < *first2){
*result = *first1;
++first1;
++result;
}
else if(*first2 < *first1){
++first2;
++result;
}
else{//*first2 == *first1
++first1;
++first2;
}
return copy(first2,last2,copy(first1,last1,result));
}

set_symmetric_difference之进行逻辑已经在源代码注释中说明得十分清楚。下图所示的是其一步步的分析图解。

6. heap算法

1. 四个heap相关算法已于4.7.2节的介绍过：make_heap(), pop_heap () , push_heap () , sort_heap()。
2. SGT STL 算法所在的头文件内包含了:#include // make_heap,push_heap,pop_heap,sort_heap

7. 其它算法

定义于SGI内的所有算法，除了set/heap相关算法已于前两节介绍过，其余都安排在这一节。其中有很单纯的循环遍历，也有很复杂的快速排序。

7.1 单纯的数据处理

1. 这一小节所列的算法，都只进行单纯的数据移动、线性查找、计数、循环遍力、 逐一对元素施行指定运算等操作。
2. 先观察每一个算法的表现，是以下程序示范本节每一个算法的用法。程序中有时使用STL内建的仿函数(functors,如 less,greater,equeal_to)和配接器(adapters,如bind2nd), 有时使用自定义的仿函数（如display,even_by _two) ;
3. 仿函数相关技术请参考1.9.6节和 第7章，配接器相关技术请参考第8章

#include
#include
#include
#include
using namespace std;

template <class T>
struct display{//这是一个仿函数
void operator()(const T& x)const
{cout<<x<<' ';}
};
struct even{//这是一个仿函数
bool operator()(int x)const
{return x%2 ? false : true;
};
class even_by_two{//这是一个仿函数。 
public: 
int operator()()const
{return _x +=2;}
private:
static int _x;
};
int even_by_two::_x = 0;

int main()
{
int ia[] = {0,1,2,3,4,5,6,6,6,7,8};
vector<int> iv(ia,ia+sizeof(ia)/sizeof(int));

//找出iv之中相邻元素值相等的第一个元素
cout << *adjacent_find(iv.begin(), iv.end()) <<endl;//6

//找出iv之中相邻元素值相等的第一个元素
cout << *adjacent_find(iv.begin(), iv.end(), equal_to<int>())<<endl;//6

//找出iv之中元素值为6的元素个数
cout << count(iv.begin(), iv.end(), 6)<<endl;//3

//找出iv之中小于7的元素个数
cout << count_if(iv.begin(), iv.end(), bind2nd(less<int>(),7 ))<<endl;//9

//找出iv之中元素值为4的第一个元素的所在位置的值
cout<<*find(iv.begin(),iv.end(),4)<<endl;//4

//找出iv之中大于2的第一个元素的所在位置的值
cout<<*find_if(iv.begin(),iv.end(),bind2nd(greater<int>(),2))<<endl;//3

//找出iv之中子序列iv2所出现的最后一个位置（再往后3个位置的值）
 vector<int> iv2(ia+6, ia+8); //{6, 6}
 cout<<*(find_end(iv.begin(),iv.end(),iv2.begin(),iv.end())+3)<<endl;//8
//找出iv之中子序列iv2所出现的第一个位置（再往后3个位置的值）
cout<<*(find_first_of(iv.begin(),iv.end(),iv2.begin(),iv2.end())+3)<<endl;//7

//迭代器遍历整个iv区间，对每一个元素施行display操作（不得改变元素内容）
for_each(iv.begin(),iv.end(0,dispaly<int>())<<endl;//iv:0 1 2 3 4 5 6 6 6 7 8
//以下错误：generate的第三个参数（仿函数）本身不得有任何参数
// generate(iv.begin(),iv.end(), bind2nd(plus() , 3)) ; // error
//以下迭代器遍历整个iv2区间，对每个元素施行even_by_two操作（得改变元素内容）
generate (iv2 . begin(),iv2.end(), even_by_two()); 
for_each(iv2.begin(),iv2.end(), display<int>());
cout<<endl;//iv2:2 4
 
//迭代遍历指定区间（起点与长度），对每个元素施行even_by_two操作（得改变元素值） 
generate_n(iv.begin(), 3, even_by_two()); 
for_each(iv.begin(), iv.end(), display<int>()); 
cout<<end;;//iv:6 8 10 3 4 5 6 6 6 7 8

//删除（但不删除）元素6。尾端可能有残余数据（可另外以容器之）
remove(iv.begin(),iv.end(),6);
for_each(iv.begin(),iv.end(),display<int>());
cout<<endl;// iv : 8 10 3 4 5 7 8  6 6 7 8(灰色表残余数据）
//删除（但不删除）元素6。结果置于另一区间
vector<int> iv3(12); 
remove_copy(iv.begin(), iv.end(), iv3.begin(), 6); 
for_each(iv3.begin(),iv3.end(),display<int>();
cout<<endl;//iv3: 8 10 3 4 5 7 8 7 8 0 0 0(灰色表残余数据)

//删除（但不删除）小于6的元素。尾端可能有残余数据

remove_if(iv.begin(),iv.end(),bind2nd(less<int>(),6);
for_each(iv.begin(),iv.end(),display<int>());
cout<<endl;//iv:8 10 7 8 6 6 7 8 6 7 8(灰色表残余数据)
//删除（但不删除）小于7的元素，结果置于另一区间
remove_cop_if(iv.begin(),iv.end(),iv3.begin(),bind2nd(less<int>(),7));
for_each(iv3.begin(),iv3.end(),display<int>());
cout<<endl;//iv3:8 10 7 8 7 8 7 8 8 0 0 0(灰色表残余数据)

//将所有的元素值6，改变为元素值3
replace(iv.begin(),iv.end(),6,3);
for_each(iv.begin(),iv.end(),display<int>());
cout<<endl;//iv:8 10 7 8 3 3 7 8 3 7 8
//将所有的元素值3, 改为元素值5结果，置于另一区间
replace_copy(iv.begin(), iv.end(), iv3.begin(), 3, 5); 
for_each(iv3 .begin(), iv3 .end(), display<int> ()); 
cout << endl; // iv3: 8 10 7 8 5 5 7 8 5 7 8 0
//将所有小于5的元素值， 改为元素值2
replace_if(iv .begin (), iv.end(), bind2nd(less<int> (), 5), 2);
for_each(iv.begin(), iv.end(), display<int>()); 
cout << endl; //iv: 8 10 7 8 2 2 7 8 2 7 8 
//将所有等于8的元素值，改为元素值9。 结果置于另一区间
replace_copy_if(iv.begin(), iv.end(), iv3.begin(), 
bind2nd(equal_to<int>(),8), 9); 
for_each(iv3.begin(), iv3.end(), display<int>()); 
cout<< endl; // i v3 : 9 10 7 9 2 2 7 9 2 7 9 0 
//逆向重排每一个元素
reverse(iv.beg1.n(), iv.end()); 
for_each(iv.begin(), iv.end(), display<int>());
cout<<endl;//iv:8 7  2 8 7 2 2 8 7 10 8

//逆向重排每一个元素。 结果置于另一区间
reverse_copy(iv.begin(), iv.end(), iv3.begin());
for_each(iv3.begin(),iv3.end(),display<int>());
cout<<endl; //iv3: 8 10 7 8 2 2 7 8 2 7 8 0

//旋转（互换元素） [first,middle)和[middle, last)
rotate(iv.begin(),iv.begin()+4,iv.end());
for_each(iv.begin(),iv.end(),display<int>());
cout<<endl;//iv: 7 2 2 8 7 10 8 8 7 2 8

//旋转（互换元素） [first,middle)和[middle, last) , 结果置于另一区间
rotate_copy(iv.begin(), iv.begin()+5, iv.end(), iv3.begin());
for_each(iv3.begin(),iv3.end(),display<int>());
cout<<endl;//iv3:10 8 8 7 2 8 7 2 2 8 7 0

//查找某个子序列的第 次出现地点
int ia2[3] = {2,8}; 
vector<int> iv4(ia2, ia.2+2); // iv4: {2,8} 
cout<< *search(iv.begin(), iv.end(), iv4.begin(), iv4.end())<<endl;//2

//查找连续出现2个8的子序列起点
cout << *search_n(iv.begin(), iv.end(), 2, 8)<< endl; // 8 
//查找连续出现3个小于8的子序列起点
cout << *search_n(iv.begin(), iv.end(), 3, 8, less<int>()) << endl; // 7

//将两个区间内的元素互换。 第二区间的元素个数不应小于第一区间的元素个数
swap_ranges(iv4.begin(), iv4.end(), iv.begin()); 
for_each(iv.begin(), iv.end(), display<int:>()); 
cou<<endl; //iv: 2 8 2 8 7 10 8 8 7 2 8 
for_each(iv4.begin(), iv4.end(), display<int:>()); // iv4: 7 2 
cout<< endl; 
//改变区间的值,全部减2
transform(iv.begin(), iv.end(), iv.begin(), bind2nd(minus<int>(),2)); for_each(iv.begin(), iv.end(), display<int>());
cout<< endl;//iv: 0 6 0 6 5 8 6 6 5 0 6 
//改变区间的值， 令笫二区间的元素值加到第一区间的对应元素身
//第二区间的元素个数不应小于第 区间的元素个数

transform(iv.begin(), iv.end(), iv.begin(), iv.begin(),plus<int>()); for_each (iv.begin(), iv.end() , display<int>()); 
cout << endl;//iv: 0 12 0 12 10 16 12 12 10 0 12 
//****************** 
vector<int> iv5(ia, ia+sizeof(ia)/sizeof(int)); 
vector<int> iv6(ia+4, ia+8); 
vector<int> iv7 (15); 
for_each(iv5.begin(), iv5.end(), display<int>()); 
cout<<endl;//iv5:0 1 2 3 4 5 6 6 6 7 8
for_each(iv6.begin(), iv6.end(), display<int>());
cout<<endl;//iv6: 4 5 6 6

cout << *max_element (iv5.begin() , iv5end()) << endl; // 8
cout << *min_element (iv5.begin() , iv5end()) << endl; // 0

//判断是否iv6内的所有元素都出现于iv5中
//注意：两个序列都必须是sorted ranges 
cout << includes(iv5.begin(), iv5.end(), iv6.begin(), iv6.end())<<endl;//1 (true)

//将两个序列合并为个序列
//注意：两个序列都必须是sorted ranges, 获得的结果也是sorted
merge(iv5.begin(), iv5.end(), iv6.begin(), iv6.end(), iv7.begin()); 
for_each(iv7.begin(), iv7.end(), display<int>());
cout<<endl;//iv7 0 1 2 3 4 4 5 5 6 6 6 6 6 7 8

//符合条件的元素放在容器前段， 不符合的元素放在后段
//不保证保留原相对次序
partition(iv7 .begin(), iv7 .end(), even()); 
for_each(iv7. begin(), iv7.end(), display<int>());
cout<<endl;//iv7: 0 8 2 6 4 4 6 6 6 6 5 5 3 7 1
//去除 “连续而重复 的元素
//注意：获得的结果可能有残余数据

unique(iv5.begin(), iv5.end()); 
for_each(iv5.begin(), iv5.end(), display<int>());
cout<<endl;//iv5:0 1 2 3 4 5 6 7 8 7 8(灰色为残余数据)
//去除“连续而重复”的元素，将结果置于另一处
//注意：获得的结果可能有残余数据
unique_copy(iv5 .begin(), iv5.end(), iv7.begin()); 
for_each(iv7.begin(), iv7.end(), display<int>());
cout<<endl;//iv7:0 1 2 3 4 5 6 7 8 7 8 5 3 7 1(灰色为残余数据)
}

1.adjacent_find
找出第一组满足条件的相邻元素。这里所谓的条件，在版本一中是指“两元 素相等“，在版本二中允许用户指定一个二元运算，两个操作数分别是相邻的第一 元素和第二元素。

//查找相邻的重复元素。版本一
template <class ForwardIterator> 
ForwardIterator adjacent_find(ForwardIterator first，ForwardIterator last) {
if(first == last)return last;
ForwardIterator next = first;
while(++next !=last){
if(*first == *next)return first;//如果找到就结束
first = next;
}
return last;
}
//查找相邻的重复元素。版本二
template <class ForwardIterator,class BinaryPredicate> 
ForwardIterator adjacent_find(ForwardIterator first,ForwardIterator last,BinaryPredicate binary_pred){
if(first == last)return last;
ForwradIterator next = first;
while(++next !=last){
//如果找到相邻的元素符合外界指定条件，就结束
//以下，两个操作数分别是相邻的第一元素和第二元素
if (binary_pred(*first, *next)) return first; 
first= next; 

}
return last;
}

2.count

运用equality操作符，将[first,last)区间内的每一个元素拿来和指定值 value比较，并返回与value相等的元素个数。

template<class InputIterator,class T>
typename iterator_traits<InputIterator>::difference_type
count(InputIterator first,InputIterator last,const T& value){
//以下声明一个计数器 n
typename iterator_traits<InputIterator>::difference_type n = 0;
for( ; first !=last;++first)//整个区间走一遍
if(*first == value)//如果元素值和value相等
++n;//计数器累加1
return n;
}

请注意，count()有一个早期版本，规格如下。它和上述标准版本的主要差异是，计数器由参数提供：

//这是旧版的count() 
template <Class InputIterator, class T, class Size>
 void count(InputIterator first, InputIterator last, const T& value,Size& n){
for( ;first !=last;++first)//整个区间走一遍
if(*first == value)//如果元素值和value相等
++n;//计数器加1
}

3.count_if

将指定操作（一个仿函数）pred实施于[first,last)区间内的每一个元素身上，并将“造成pred之计算结果为true"的所有元素的个数返回．

template<class InputIterator,class Predicate>
typename iterator_traits<InputIterator>::difference_type
count_if(InputIterator first,InputIterator last,Predicate pred){
//以下声明一个计数器n
typename iterator_traits<InputIterator>::difference_type n = 0;
for( ;first !=last;++first)//整个区间走一遍
if(pred(*first))//如果元素带入pred的运算结果为true
++n;//计数器加1
return n;
}

请注意，count_if()有一个早期版本，规格如下。它和上述标准版本的主要 差异是，计数器由参数提供：

//旧版count_if()
template <class InputIterator,class Predicate, class Size> 
void count_if(InputIterator first, InputIterator last, Predicate pred, Size& n) {
for( ; first !=last;++first)//整个区间走一遍
if(pred(*frist))//如果元素带入pred的运算结果为true
++n;//计数器加1
}

4.find

根据equality操作符，循序查找［first,last）内的所有元素，找出第一个 匹配”等同(equality)条件”者。如果找到，就返回一个lnputlterator指向该元 素，否则返回迭代器last。

template <class InputIterator, class T> 
InputIterator find(InputIiterator first, InputIterator last,const T& value){
while(first !=last && *first !=value)++first;
return first;
}

5.find_if

根据指定的pred运算条件（以仿函数表示），循序查找［first,last)内 的所有元素，找出第一个令pred运算结果为true者。如果找到就返回一个 lnputIterator指向该元素，否则返回迭代器last。

template <class InputIterator, class Predicate>
InputIterator find_if(InputIterator first, InputIterator last,Predicate pred){
while(first !=last && !pred(*first))++first;
return first;
}

6.find_end
在序列一[first1,last1)所涵盖的区间中，查找序列二[first2,last2)的最后一次出现点。如果序列一之内不存在“完全匹配序列二＂的子序列，便返回迭代器last1。此算法有两个版本，版本一使用元素型别所提供的equality操作 符，版本二允许用户指定某个二元运算（以仿函数呈现），作为判断元素相等与否 的依据。以下只列出版本一的源代码。

由于这个算法查找的是“最后一次出现地点”，如果我们有能力逆向查找，题目就变成了“首次出现地点”，那对设计者而言当然比较省力。逆向查找的关键在于迭代器的双向移动能力，因此，SGI将算法设计为双层架构，一般称呼此种上层函数为dispatch functiion(分配函数、派送函数）：

//版本1
template<class ForwardIterator1,class ForwardIterator2>
inline ForwardIterator1
find_end(ForwardIterator1 first1,ForwardIterator1,last1,ForwardIterator2 first2,ForwardIterator2,last2,){
typedef typename iterator_traits<ForwardIterator1>::iterator_category category1;
typedef typename iterator_traits<ForwardIterator2>::iterator_category category2;

//以下根据两个区间的类属，调用不同的下层函数
return __find_end(first1,last1,first2,last2,category1(),category2());
}

这是一种常见的技巧，令函数传递调用过程中产生迭代器类型(iterator category)的临时对象(型别名称之后直接加一对小括号，便会产生一个临时对象）,再利用编译器的参数推导机制(argument deduction) 动调用某个对应函数。此例之对应函数有两个候选者：

//以下是forward iterator版

template<class ForwardIterator1,class ForwardIterator2>
ForwardIterator1 __find_end(ForwardIterator1 first1, ForwardIterator1 last1,ForwardIterator2 first2, ForwardIterator2 last2,forward_iterator_tag,forward_iterator_tag)
{
if (first2 == last2) //如果查找目标是空的，
return last1; //返回last1, 表示该 “空子序列＂ 的最后出现点 
else { 
ForwardIteraor1 result = last1; 
while(1){ 
//以下利用search()查找某个子序列的首次出现点。 找不到的话返回last1
ForwardIterator1 new_result = search(first1, last 1, first2, last2); 
if(new_result== last1) //没找到
return result;
else{ 
result = new_result; //调动一下标兵， 准备下一个查找行动 
first1 = new_result; 
++first1; 
   }
  }
 }
}

//以下是bidirectional iterators版（可以逆向查找）
template <class BidirectIonaliterator1, class Bidirectiona1Iterator2> BidirectionalIterator1
__find_end(BidirectionalIteratorl first 1, BidirectionalIteratorl last1,BidirectionalIterator2 first2, BidirectionalIterator2 last2, bidirectional_iterator_tag,bidirectional_iterator_tag))
{
//由于查找的是 “最后出现地点” ，因此反向查找比较快。 利用reverse_iterator .
// reverse_iterator见本书第8章
typedef reverse_iterator<BidirectionalIterator1> reviter1;
typedef reverse_iterator<BidirectionalIterator2> reviter2; 
reviter1 rlast1(first1);
reviter2 rlast2(first2);

//查找时， 将序列一和序列二统统逆转方向
reviter1 rresult = search(reviter1(last1), rlast1,reviter2(last2),rlast2);

if (rresult == rlast1) //没找到
return last1; 
else { //找到了
BidirectionalIterator1 result = rreimlt.base(); //转回正常（非逆向）迭代器 
advance(result, -distance(first2, last2)}; //调整回到子序列的起头处
return result; 
}
}

为什么最后要将逆向迭代器转回正向迭代器， 而不直接移动逆向迭代器呢？因为正向迭代器和逆向迭代器之间有奇妙的"实体关系"和“逻辑关系”。(详见8.3.2)。

7.find_first_of

1. 本算法以［first2,last2)区间内的某些元素作为查找目标，寻找它们在(first1,last1)区间内的第一次出现地点。
2. 举个例子，假设我们希望找出字符序列synesthesia的第一个元音，我们可以定义第二序列为aeiou。
3. 此算法会返回一个ForwardIterator,指向元音序列中任一元素首次出现于第一序列的地点，此列将向字符序列的第一个e。
4. 如果第一序列并未内含第二序列的任何元素，返回的将是 last1。本算法第一个版本使用元素型别所提供的equality操作符，第二个版本允许用户指定一个二元运算pred。

//版本一
template <class InputIterator, class ForwardIterator> 
InputIterator find_first_of(InputIterator first1, InputIterator last1,ForwardIterator first2, ForwardIterator last2)
{
	for( ;first1 !=last1;++first1)//遍历序列一
	//以下，根据序列二的每个元素
	for(ForwardIterator iter = first2;iter !=last2;++iter)
	if(*first1 == *iter)//如果序列一的元素等于序列二的元素
	return first1;//找到，结束
	return last1;
}

//版本二
template <class InputIterator,class ForwardIterator, class BinaryPredicate> 
InputIterator find_first_of(InputIterator first1,InputIterator last1,ForwardIterator first2,ForwardIterator last2,BinaryPredicate comp)
{
for( ;first1 !=last1;++first1)//遍历序列一
//以下，根据序列二的每个元素
for(ForwardIterator iter = first2;iter !=last2;++iter)
if(comp(*first,*iter))//如果序列一和序列二的元素满足comp条件
return first1;//找到了，结束
return last1;
}

8.for_each

将仿函数f施行于[first,last)区间内的每个元素身上。f不可以改变元素内容，因为first和last都是lnputlterators, 不保证接受赋值行为(assignment)。如果想要一一修改元素内容，应该使用算法transform()。f可返回一个值，但该值会被忽略。

template<class InputIterator,class Function>
Function for_each(InputIterator first,InputIterator last,Function f){
for( ;first !=last;++first)
f(*first);//调用仿函数f的function call操作符。返回值被忽略
return f;
}

9.generate

将仿函数gen的运算结果填写在[first,last)区间内的所有元素身上。 所谓填写， 用的是迭代器所指元素之assignment操作符。

template<class ForwardIterator,class Generator>
void generate(ForwardIterator first,ForwardIterator last,Generateor gen){
for( ; first !=last;++first)//整个序列区间
*first = gen();
}

10.generate_n

将仿函数gen的运算结果填写在从迭代器first开始的n个元素身上。所谓填写，用的是迭代器所指元素的assignment操作符。

template <class OutputIterator, class Size, class Generator>
OutputIterator generate_n(OutputIterator first, Size n, Generator gen) {
for( ;n>0;--n,++first)//只限n个元素
*first = gen();
return first;
}

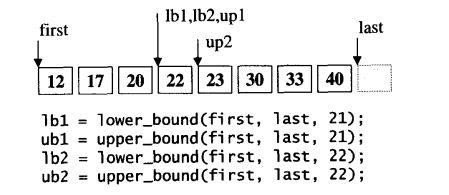
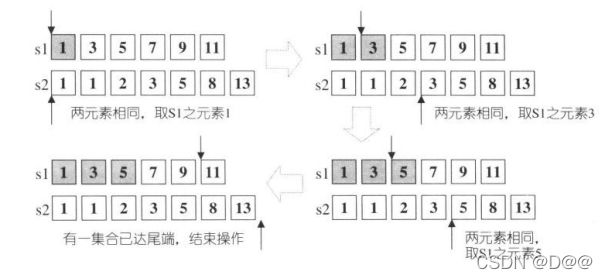
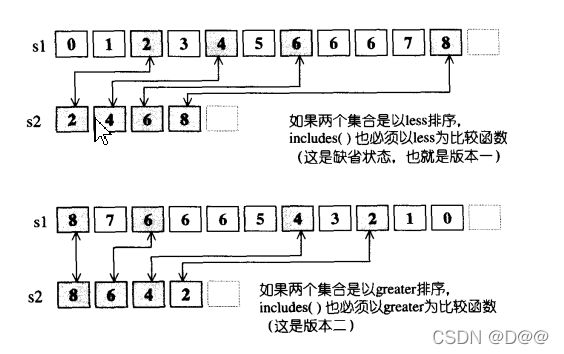
11.includes (应用于有序区间）

1. 判断序列二S2是否"涵盖于 " 序列一S1。
2. S1和S2都必须是有序集合，其中的元素都可重复（不必唯一）。
3. 所谓涵盖， 意思是 “s2的每一个元素都出现于S1”。
4. 由于判断两个元素是否相等， 必须以less或greater运算为依据（当S1元素不小于S2元素且S2元素不小于S1元素，两者即相等；或说当S1元素不大于 S2元素且S2元素不大于S1元素， 两者即相等）。 因此配合着两个序列Sl和S2 的排序方式（递增或递减），includes算法可供用户选择采用less或greater 进行两元素的大小比较(comparison)。

换句话说，如果S1和S2是递增排序（以operator<执行比较操作）,includes算法应该这么使用：

includes(S1.begin(),S1.end(),S2.begin(),S2.end());

这和下一行完全相同：

includes(S1.begin(),S1.end(),S2.begin(),S2.end(),less<int>());

然而如果Sl和S2是递减排序（以operator>执行比较操作），includes算 法应该这么使用：

includes(S1.begin(), S1.end(), S2.begin(), S2.end(), greater<int>());

注意， S1或S2内的元素都可以重复， 这种情况下所谓 "s1内含一个S2子集合” 的定义是：假设某元素在S2出现n次， 在S1出现m次， 那么如果m< n, 此算法会返回false。
下图是includes算法的工作原理：

下面是includes算法的两个版本的源代码:

//版本一。判断区间二的每个元素值是否都存在于区间一
//前提一：区间一和区间二都是sorted ranges
template<class InputIterator1,class Inputerator2>
bool include<InputIterator1 first1,Inputerator1 last1,InputIterator2 first2,Inputerator2  last2){
while(first1 !=last1 && first2 !=last2)//两个区间都尚未走完
if(*first2 <*first1)//序列二的元素小于序列一的元素
return false;//"涵盖”的情况必然不成立。结束执行
else if(*first1<*first2)//序列二的元素大于序列一的元素
++first1;//序列一前进1
else//*first1 == *first2
++first1,++first2;//都前进1
return first2 == last;//有一个序列走完了，判断最后一关
}

//版本二。判断序列一内是否有个子序列，其与序列二的每个对应元素都满足二元运算comp 
//前提：序列一和序列二都是sorted ranges 
template <class InputIterator1, class InputIterator2,class Compare> 
bool includes(InputIterator1 first1, InputIterator1 last1, InputIterator2 first2, InputIterator2 last2, Compare comp){
while(first1 = last1 && first2 !=last)//两个区间都没有走完
if(comp(*first2,*first1))//comp(S2元素，S1元素)为真
return false;//“涵盖”的情况必然不成立，结束
else if(comp(*first1,*first2))//comp(S1元素，S2元素)为真
++first1;//S1前进1
else
++first1,++first2;//S1,S2各前进1
return first2 == last2;//有一个序列走完了，判断最后一关
}

从版本二可知，如果你传入一个二元元素comp,却不能使用以下的case3代表“两元素相等”:

if (comp(*first2, *firstl))	//case1
...
else if(comp(*first2，*first2))	// case2
...
else		//case3

这个comp将会造成整个includes算法语意错误。但同时comp的型别是Compare,既不是BinaryPredicate,也不是BinaryOperation,所以并非随便一个二元运算就可拿来作为comp的参数。从这里我们得到一个教训，是的，虽然从语法上来说Compare只是一个template参数（从这个观点看，它叫什么名称都一样），但它（乃至于整个STL的符合命名）有其深刻涵义。

12.max_element
这个算法返回一个迭代器，指向序列之中数值最大的元素。其中工作原理至为简单，下面是两个版本的源代码：

//版本一
template <class ForwardIterator> 
ForwardIterator max_element(ForwardIterator first, ForwardIterator last){
if (first==last)return first;
 ForwardIterator result= first; 
 while (++first != last) 
 if(*result< *first) result= first; //如果目前元素比较大，就登记起来
 return result;
 }

//版本二
template <class ForwardIterator, class Compare> 
ForwardIterator max_element(ForwardIterator first, ForwardIterator last,Compare comp){
if (first== last)return first; 
ForwardIterator result=first;
while (++first != last)
if (comp(*result,*first))result= first;
return result; 
}

13.merge (应用于有序区间）

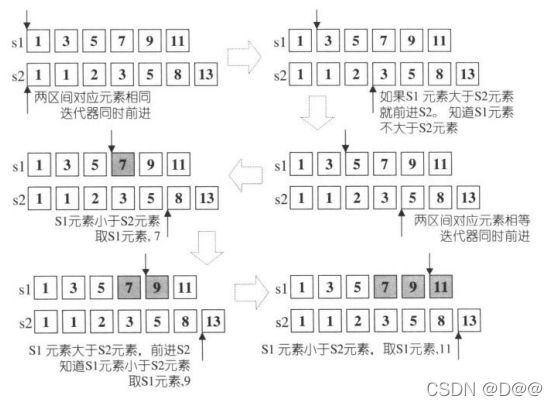
将两个经过排序的集合S1和S2,合并起来置于另一段空间，所得结果也是一个有序（sorted）序列。返回一个迭代器，指向最后结果序列的最后一个元素的下一位置。下图展示merge算法的工作原理。下面是merge算法的两个版本的源代码：

//版本一
template <class InputIterator1, class InputIterator2,class OutputIterator> 
OutputIterator merge(InputIterator1 first1, InputIterator1 last1,InputIterator2 first2, InputIterator2 last2,OutputIterator result){
while (first1 ! = last1 && first2 ! = last2){ //两个序列都尚未走完
if(*first2 < *first1){
*result = *first2;//登记序列二的元素
++first2;//序列二前进1
}else
{
*result = *first1;//登记序列一元素
++first1;///序列一前进1
}
++result;
}
// 最后剩余元素以copy复制到目的端。以下两个序列 定至少有一个为空
return copy(first2, last2,copy (first1, last1,result));
}

//版本二
template<class InputIterator1,class InputIterator2,class OutputIterator,class Compare>
OutputIterator aerge(InputIterator1 first1, InputIterator1 last1,InputIterator2 first2, InputIterator2 last2,OutputIterator result, Compare comp){ 
while (first! != last1 && first2 != last2){//两个序列都尚未走完
if(comp(*first2,*first1)){//比较两序列的元
*result = *first2;//登记序列二的元素
++first2;//序列二前进1
}
else{
*result = *first1;//登记序列一的元素
++first1;//序列一前进1
}
++result;
}
//最后剩余元素以copy复制到目的端。以下两个序列定至少有一个为空
return copy(first2, last2, copy(first1, last1,result));
}

14.min_element

这个算法返回一个迭代器，指向序列之中最小的元素。其工作原理至为简单，下面是两个版本的源代码：

//版本 一
template <class Forwarditerator> 
Forwarditerator min_element(ForwardIterator first, ForwardIterator last) {
if (first == last) return first; 
ForwardIterator result = first; 
while (++first != last)
if (*first < *result) result = first; //如果目前元素比较小， 就登记起来 return result;
}
//版本二
template <class ForwardIterator, class Compare>
ForwardIterator min_element(ForwardIterator first, ForwardIterator last,Compare comp) { 
if (first == last) return first; 
ForwardIterator result = first; 
while (++first != last)
if(comp (*first, *result)) result = first; 
return result;
}

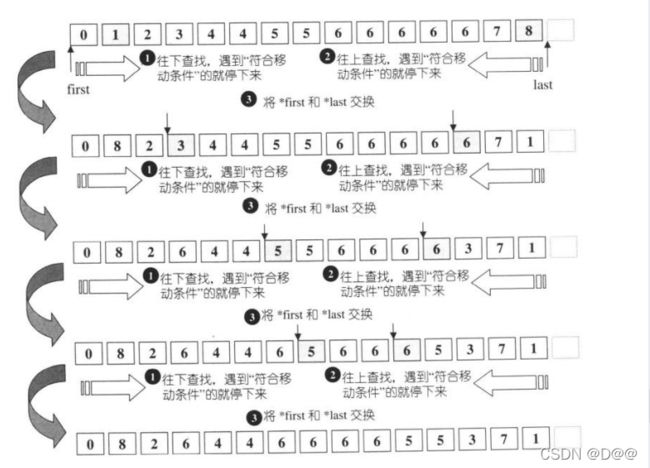
15.partition

partition会将区间[first,last)中的元素重新排列。 所有被一元条件运算pred判断为true的元素，都会被放在区间的前段，被判定为false的元素，都会被放在区间的后段。 这个算法并不保证保留元素的原始相对位置。如果需要保留原始相对位置， 应使用stable_partition。下面是partition算法的源代码。 其工作原理见下图。

//所有被pred判定为true的元素， 都被放到前段
//被pred判定为falise的元素， 都被放到后段
//不保证保留原相对位置。 (not stable) 
template <class BidirectionalIterator, class,Predicate> 
	BidirectionalIterator partition(BidirectionalIterator first,BidirectionalIterator last, Preicate pred){
	while(true){
	while(true)
	if(first == last)//头指针等于尾指针
	return first;//所有操作结束
	else if(pred(*first))//头指针所指的元素符合不移动条件
	++first;//不移动；头指针前进1
	else//头指针所指元素符合移动条件
	break;//跳出循环
	--last;//尾指针回溯1
	while(true)
	if(first == last)//头指针等于尾指针
	return first;//所有操作结束
	else if(!pred(*last))//尾指针所指的元素符合不移动条件
	--last;//不移动；尾指针回溯1
	else//尾指针所指元素符合移动条件
	break;//跳出循环
	iter_swap(first,last);//头尾指针所指元素彼此交换
	++first;//头指针前进1,准备下一个外循环迭代
	}
}

本例所谓的移动条件（亦即所选用的pred）是一个“判断数值是否为偶数”的仿函数。

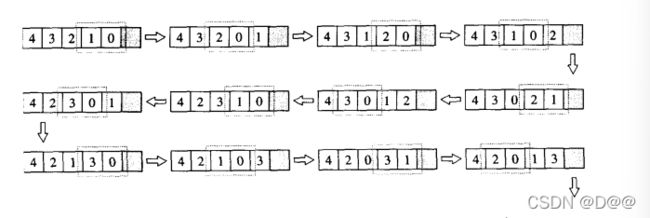
16.remove移除（但不删除）

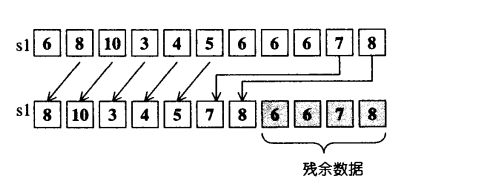
1. 移除[first,last)之中所有与value相等的元素。
2. 这算法并不真正从容器中删除那些元素（换句话说容器大小并未改变），而是将每一个不与value相等（也就是我们并不打算移除）的元素轮番赋值给first之后的空间。
3. 返回值 Forwardlterator标示出重新整理后的最后元素的下一位置。
4. 例如序列{0,1,0,2,0,3,0,4}, 如果我们执行remove(), 希望移除所有0值元素，执行结果将 是{1,2,3,4,0,3,0,4｝。每一个与0不相等的元素，1,2,3,4,分别被拷贝到第一、二、三、四个位置上。第四个位置以后不动，换句话说是第四个位置之后是这一算法留下的残余数据。返回值Forwardlterator指向第五个位置。
5. 如果要删除那些残余数据，可将返回的迭代器交给区间所在之容器的erase() member function。注意， array不适合使用remove()和remove_if () , 因为array无法缩小尺寸，导致残余数据永远存在。对array而言，较受欢迎的算法是remove_copy ()和 remove_copy _if ()。

template <class ForwardIterator,class T>
ForwardIterator remove(ForwardIterator first ForwardIterator last,const T& value) { 
first= find(first, last, value); //利用循序查找法找出第一个相等元素
 ForwardIterator next=first;//以next标示出来
// 以下利用“remove_copy()允许新旧容器重叠”的性质，进行移除操作
//井将结果指定置于原容器中
return first== last ? first : remove_copy(++next, last, first, value);
}

移除(remove)所有数值为6的元素。如果运算结果置于另一个区间（而非如本图在同一个s1区间上）即是remove_copy算法。

下一个图对remove算法的程序操作另有良好的说明：尽管该图是针对更一般化的pred条件，而非本处的”相等(equality)条件。

17.remove_copy

移除[first，last)区间内所有与value相等的元素。它并不真正从容器中删 除那些元素（换句话说，原容器没有任何改变），而是将结果复制到一个以result 标示起始位置的容器身上。新容器可以和原容器重叠，但如果对新容器实际给值时， 超越了旧容器的大小，会产生无法预期的结果。返回值Outputlterator指出被复制 的最后元素的下一位置。

template <class InputIterator, class OutputIterator, class T> 
OutputIterator remove_copy(InputIterator first, InputIterator last,OutputIterator result, const T& value) {
for (; first != last; ++first) 
if (*first!=value){
*result= *first; //就赋值给新容器
++result;//新容器前进一个位置
}
return result;
}

18.remove_if

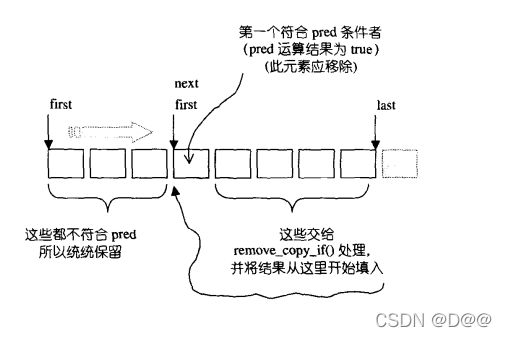
1. 移除［first,last)区间内所有被仿函数pred核定为true的元素。
2. 它并不真正从容器中删除那些元素（换句话说，容器大小并未改变，请参考remove())。每一个不符合pred条件的元素都会被轮番赋值给first之后的空间。
3. 返回值Forwardlterator标示出重新整理后的最后元素的下位置。
4. 此算法会留有些残余数据，如果要删除那些残余数据，可将返回的迭代器交给区间所在之容器的erase() member function. 注意，array不适合使用remove()和remove_if(),因为array无法缩小尺寸，导致残余数据永远存在。对array而言，较受欢迎的算法是 remove_copy ()和remove_copy_if()。

template <class ForwardIterator, class Predicate> 
ForwardIterator remove_if(ForwardIterator first, ForwardIterator last,Predicate pred){ 
first= find_if(first,last,pred); //利用循序查找法找出第一个匹配者
ForwardIterator next = first;//以next标记出来
//以下利用"remove_copy_if()允许新旧容器重叠 ”的性质，做删除操作
//并将结果放到原容器中
return first== last ? first : remove_copy_if(++next, last, first, pred);
}

remove_if操作示意图：

19.remove_copy _if

移除[first,last)区间内所有被仿函数pred评估为true的元素。它并不真正从容器中删除那些元素（换句话说原容器没有任何改变），而是将结果复制到一个以result标示起始位置的容器身上。 新容器可以和原容器重叠， 但如果针对新容器实际给值时， 超越了旧容器的大小， 会产生无法预期的结果。 返回值Outputlterator指出被复制的最后元素的下 位置。

template <class InputIterator ,. class OutputIterator, class Predicate> 
OutputIterator remove_copy_if(InputIterator first,InputIterator last,OutputIterator result,Predicate pred)[
for (; first ! = last; ++first)
if (!pred(*first)) //如果pred核定为false,
*result = *first; (就赋值给新容器（保留， 不删除）
++result;//新容器前进一个位置
}
return result;
}

20 .replace

将[first，last)区间内的所有old_value都以new_value取代。

template <class ForwardIterator, class T> 
void replace(ForwardIterator first, ForwardIterator last, const T& old_value,const T& new_value) {
//将区间内的所有old_value都以new_value取代 
for (; first !=last;++first) 
if (*first==old_value) *first=new_value;
}

21.replace_copy

行为与replace()类似，唯一不同的是新序列会被复制到result所指的容器中。返回值Outputlterator指向被复制的最后一个元素的下一位置，原序列没有任何改变。

template <class InputIterator, class OUtputIterator, class T> 
OUtputIterator replace_copy(InputIterator first, InputIterator last,OutputIterator result, const T& old_value,const T& new_value){
for (; first != last; ++first, ++result) 
//如果旧序列上的元素等于old_value,就放new_value到新序列中
//否则就元素拷贝一份放进新序列中
*result = *first == old_value ? new_value : *first;
return result;
}

22.repalce_if

将[first,last)区间内所有”被pred评估为true"的元素，都以 new_value取而代之。

template <class ForwardIterator, class Predicate, class T>
 void replace_if(ForwardIterator first, ForwardIterator last,Predicate pred,const T& new_value){
 for (; first!=last; ++first)
 if (pred(*first))*first= new_value;
 }

23.replace_copy_if

行为与replace_if(）类似，但是新序列会被复制到result所指的区间内。返回值Outputlterator指向被复制的最后一个元素的下一位置。原序列无任何改变。

template <class Iterator, class OutputIterator, class Predicate, class T> 
OutputIterator replace_copy_if(Iterator first, Iterator last, OutputIterator result, Predicate pred, const T& new_value) { 
for (; first ! = last; ++first, ++result)
//如果旧序列上的元素被pred评估为true,就放new_value到新序列中，
//否则就将元素拷贝 份放进新序列中
result = pred(*first) ? new_value : *first;
return result;
}

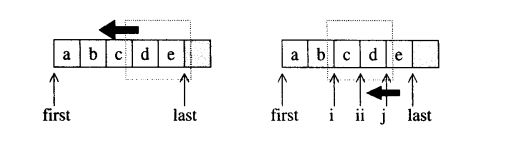
24.reverse

将序列[first,last)的元素在原容器中颠倒重排。例如序列{0,1,1,3,5}颠倒重排后为{5,3,1,1,0}。 迭代器的双向或随机定位能力，影响了这个算法的效率， 所以设计为双层架构：

//分派函数(dispatchfunction) 
template <class BidirectionalIterator> 
inline void reverse(BidirectionalIterator first, BidirectionalIterator last){
_reverse(first, last, iterator_category(first));
}

// reverse的bidirectional iterator版 
template <class BidirectionalIterator> 
void __reverse(BidirectionalIterator first,BidirectionalIterator last,bidirectional_iterator_tag){
while(true)
if(first == last || first == --last)
return;
else
iterator_swap(first++,last);
}

// reverse的random access iterator版
template <class RandornAccessIterator>
void reverse(RandornAccessIterator first, RandornAccessIterator last,randorn_access_iterator_tag) { 
//以下，头尾两两互换，然后头部累进一个位置，尾部累退个位置。 两者交错时即停止
//注意， 只有random iterators才能做以下的first < last判断
while (first < last) iter_swap(first++, --last); 
}

25.reverse_copy

行为类似reverse(), 但产生出来的新序列会被置于以result指出的容中。
返回值Outputlterator指向新产生的最后元素的下 位置。 原序列没有任何改变。

template <class BidirectionalIterator, class OutputIterator> OutputIterator reverse_copy(BidirectionalIterator first, Bidirect ionalIterator last,OutputIerator result){
while (first != last) { //整个序列走一遍
--last; //尾端前移一个位置
*result = *last;//将尾端所指元素复制到result所指位置
 ++result; //resu让前进一 个位置
 }
 return result;
 }

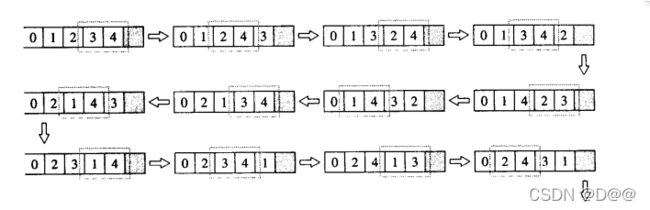
26.rotate

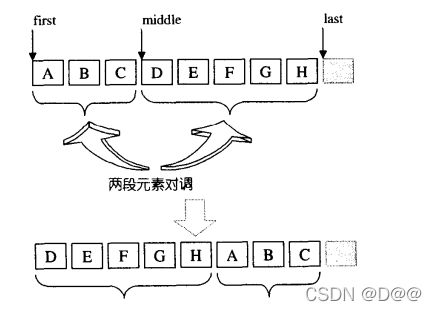
将[first.middle)内的元素和[middle,last)内的元素互换。middle所指 的元素会成为容器的第一个元素。如果有个数字序列{1,2,3,4,5,6,7}, 对元素3做旋转操作，会形成{3,4,5,6,7,1,2}。看起来这和swap_ranges()功能颇为近似，但swap_ranges ()只能交换两个长度相同的区间，rotate()可以交换两个长度不同 的区间，如下图所示。

迭代器的移动能力，影响了这个算法的效率，所以设计为双层架构：

//分派函数(dispatch function) 
template <class ForwardIterator> 
inline void rotate(ForwardIterator first, ForwardIterator middle,ForwardIterator last){
if {first == middle || middle== last) return; 
__rotate(first, middle, last, distance_type(first),iterator_category(first));
}

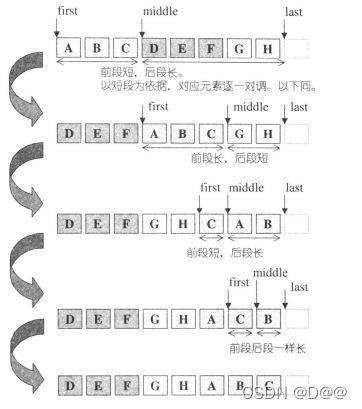
下面是根据不同的迭代器类型而完成的三个旋转操作：

// rotate的forward iterator版，操作示意如下图
template <class ForwardIterator, class Distance>
void rotate(ForwardIterator first, ForwardIterator middle,ForwardIterator last, Distance*, forward_iterator_tag) {
for(ForwardIterator i = middle; ;){

iter_swap(first, i);//前段、后段的元素一一交换
 ++first; //双双前进1
 ++i;
 //以下判断是前段[first, middle)先结束还是后段[middle,last)先结束
if (first == middle){//前段结束了
if (i == last) return;//如果后段同时也结束，整个结束
 middle = i; //否则调整，对新的前、后再作交换
}
else if(i == last)//后段先结束
i = middle;//调整，准备对新的前、后段再作交换
}
}

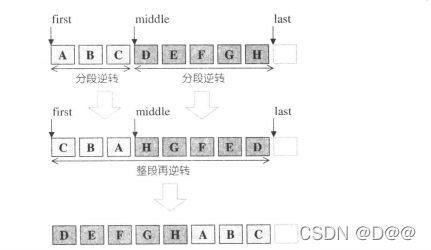
//rotate的bidirectional iterator版，操作示意如下图。
template <class BidirectionalIterator, class Distance> 
void rotate(BidirectionalIterator first, BidirectionalIterator middle,BidirectionalIterator last, Distance*,bidirectional_iterator_tag){
reverse(first, middle); 
reverse(middle, last); 
reverse(first， last);
}

//rotate的random access iterator版
template <class RandomAccessIterator, class Distance>
void __rotate(RandomAccessIterator first, RandomAccessIterator middle,RandomAccessIterator last, Distance*,random_access_iterator_tag) { 
//以下迭代器的相减操作， 只适用于random access iterators 
//取全长和前段长度的最大公因子
Distance n = _gcd(last-first, middle -first);
 while (n--) 
 __rotate_cycle(first, last,first+n, middle-first,value_type(first));
 }
//最大公因子，利用辗转相除法
// __gcd()应用于_rotate(}的randomaccess iterator版
template<class EuclideanRingElement>
EuclideanRingElement _gcd(EuclideanRingElement m, EuclideanRingElement  n) 
{ 
while (n != 0) {
EuclideanRingElement t = m % n;
m = n; 
n = t;
}
return m;
}

template <class RandomAccessIterator, class Distance, class T>
void __rotate_cycle(RandomAccessIterator first, RandomAccessIterator last,RandomAccessIterator initial,Distance shift, T*) {
T value = *initial; 
RandomAccessIterator ptr1 = initial; 
RandomAccessiterator ptr2 = ptr1+ shift; 
while (ptr2 != initial) { 
*ptr1 = *ptr2;
 ptr1 = ptr2; 
if(last-ptr2 > shift) 
ptr2 += shift; 
else 
ptr2 = first + (shift - (last - ptr2));
}
*ptr1 = value;
}

rotate forward iterator版操作示意：

rotate bidirection iterator版操作示意：

27.rotate_copy

1. 行为类似rotate(), 但产生出来的新序列会被置于result所指出的容器中。返回值Outputlterator指向新产生的最后元素的下一位置。原序列没有任何改变。
2. 由于它不需要就地(in-place)在原容器中调整内容，实现上也就简单得多。 旋转操作其实只是两段元素彼此交换，所以只要先把后段复制到新容器的前端，再 把前段接续复制到新容器，即可。

template<class ForwardIterator, class outputIterator>
OutputIterator rotate_copy(ForwardIterator first, ForwardIterator middle,ForwardIterator last, OutputIterator result) {
return copy(first, middle, copy(middle, last,result));
}

28.search

在序列一［first1,last1）所涵盖的区间中，查找序列二[first2,las2)的首次出现点。如果序列一内不存在与序列二完全匹配的子序列，便返回迭代器 last1。版本一使用元素型别所提供的equality操作符，版本二允许用户指定某个二 元运算（以仿函数呈现），作为判断相等与否的依据。以下只列出版本一的源代码。

//查找子序列首次出现地点
//版本一
template <class ForwardIterator1, class Forwarditerator2> 
inline Forwarditerator1 search(ForwardIerator1 first1, ForwardIterator1 last1, ForwardIterator2 first2, ForwardIterator2 last2) 
{
return _search(first1, last1, first2, last2, distance_type(first1),distance_type(first2));
}

template <class ForwardIterator1, class ForwardIterator2,class Distance1,class Disrance2>

ForwardIterator1 _search(ForwardIterator1 first1, ForwardIterator1 last1,ForwardIterator2 first2, ForwardIterator2 last2, Distance1*, Distance2*) { 
Distanceld1=O; 
Distance(first1,last1, d1); 
Distance2 d2 = O; 
distance(first2, last2, d2);

if(d1<d2)return last1;//如果第二序列大于第一序列不可能成为其子序列
ForwardIerator1 current1= first1;
ForwardIterator2 current2 =first2;

while (current2! = last2)//遍历整个第二序列
if(*current1 == *current2) {//如果这个元索相同
++current1; 
++current2;
}
else{//如果这个元素不等
if(d1 == d2)//如果两序列样长
return last1;//表示不可能成功了
else {//两序列不一样长（至此肯定是序列一大于序列二）
current1 = ++first1;//调整第一序列的标兵，
current2 = first2;//准备在新起点上再找
--d1;
}
}
return first1;//已经排除了序列一的一个元素， 所以序列一 的长度要减1
}

29.search_n

在序列[first ,last)所涵盖的区间中， 查找 “连续count个符合条件之元素”所形成的子序列，并返回一个迭代器指向该子序列起始处。如果找不到这样 的子序列，就返回迭代器last。上述所谓的“某条件”，在search_n版本一指的是相等条件 “equality” , 在search_n版本二指的是用户指定的某个二元运算（以仿函数呈现）。

例如，面对序列(10,8, 8, 7, 2, 8, 7, 2, 2, 8, 7, 0}, 查找“连续两个8"所形成 的子序列起点，可以这么写：

iter1 = search_n(iv.begin(),iv.end(),2,8);

查找“连续三个小于8的元素”所形成的子序列起点，可以这么写：

iter2 = search_n(iv.begin(),iv.end(),3,8,less<int>();

下图执行结果：

search_n能够找出"符合某条件之连续n个元素”的起始点

下面是search_n的源代码，其工作原理如下图所示。

//版本一
//查找“元素value连续出现count次”所形成的那个子序列，返回其发生位置 
template<classForwardIterator,class Integer, class T> 
ForwardIterator search_n(ForwardIterator first, ForwardIterator last, 
Integer count,const T& value) {
if (count<= 0) 
return first;
else { 
first= find(first, last,value);//首先找出value第一次出现点
while(first !=last){//继续查找余下元素
Iuteger n = count -1 ;//value还应出现n次
ForwardIterator i = first;//从上次出现点接下去查找
++i;
while(i !=last && n !=0 && *i == value){//下个元素是value ,good
++i;
--n;///既然找到了，"value应再出现次数”便可减1
}
if(n==0)// n==0 表示确实找到了“元素值出现n次”的子序列。功德圆满
return first;
else	//功德尚未圆满...
first = find(i,last,value);//找value的下一个出现点，并准备回到外循环
}
return last;
}
}


//版本二
//查找“连续count个元素皆满足指定条件”所形成的那个子序列的起点，返回其发生位置 

template<class Forwarditerator, class Integer. class T, class BinaryPredicate>
ForwardIterator search_n(ForwardIterator first,ForwardIterator last,Integer count,const T& value,BinaryPredicate binary_pred){
if(count<=0)
return first;
else{
while(first !=last){
if(binary_pred(*first,value)) break;//首先找出第一个符合条件的元素
++first;//找到就离开
}
while(first !=last){//继续查找余下元素
Integer n = count-1;//还应有n个连续元素符合条件
 ForwardIterator i = first; //从上次出现点接下去查找
 ++i; 
 //以下循环确定接下来count-1个元素是否都符合条件
while (i != last && n != 0 && binary_pred(*i, value)) {
++i;
--n;//既然这个元素符合条件， “应符合条件的元素个数” 便可减1
}

if (n == 0)// n==O表示确实找到了count个符合条件的元素。 功德圆满
return first;
else {//功德尚未圆满 ..
while(i !=last){
if(binary_pred(*i,value))break;//查找下一个符合条件的元素
++i;
}
first = i;//准备回到外循环
}
}
return last;
}
}

30.swap_ranges

将[first1,last1)区间内的元素与“从first2开始、个数相同”的元素互相交换。这两个序列可位于同一容器中，也可位于不同的容器中。如果第二序列 的长度小于第一序列，或是两序列在同一容器中且彼此重叠，执行结果未可预期。 此算法返回一个迭代器，指向第二序列中的最后一个被交换元素的下一位置。

//将两段等长区间内的元素互换
template<class ForwardIterator1, class ForwardIterator2> 
ForwardIterator2 swap_rangs(ForwardIterator1 first1,ForwardIterator1 last1,ForwardIterator2 first2){
for (; first1 != last1; ++first1, ++first2) 
iter_swap(first1,first2); 
return first2;
}

31.transform

1. tranforrn ()的第一版本以仿函数op作用于[first,last)中的每一个元素身上，并以其结果产生出一个新序列。
2. 第二版本以仿函数binary_op作用于一双元素身上（其中一个元素来自[firs1,last),另一个元素来自“从first2开始的序列”），并以其结果产生出一个新序列。
3. 如果第二序列的元素少于第一序列， 执行结果未可预期。
4. transform ()的两个版本都把执行结果放进迭代器result所标示的容器中。result也可以指向源端容器，那么transform()的运算结果就会取代该容器内的元素。返回值OutputIterator将指向结果序列的最后元素的下一位置。

//版本一
template <class InputIterator,class OutputIterator, class UnaryOperation> 
OutputIterator transform(InputIterator first, InputIterator last, OutputIterator result, UnaryOperation op) {
for (; first != last; ++first, ++result) 
*result= op(*first);
return result; 
}

//版本二
template <class Inputlterator1, class Inputiterator2, class Output Iterator, 
class BinaryOperation>
outputIterator transform(InputIterator1 first1, InputIterator1 last1, 
 InputIterator2 last2, Outputiterator result,BinaryOperation binary_op) { 
for (; first1 ! = last1;++first1, ++first2, ++result) 
*result= binary_op(*first1,*first2);
return result;
}

32.unique

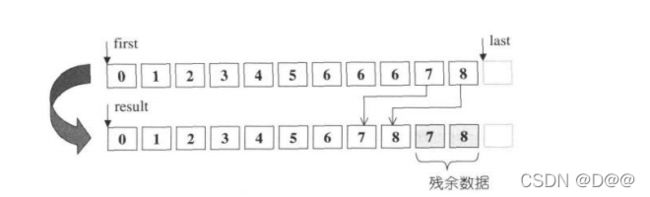
1. 算法unique能够移除(remove)重复的元素。 每当在［first,last]内遇有重复元素群， 它便移除该元素群中第一个以后的所有元素，注意,unique只移除相邻的重复元素，如果你想要移除所有（包括不相邻的）重复元素， 必须先将序列排序， 使所有重复元素都相邻。
2. unique会返回一个迭代器指向新区间的尾端， 新区间之内不含相邻的重复元
   素。 这个算法是稳定的(stable) , 亦即所有保留下来的元素，其原始相对次序不变。
3. 事实上unique并不会改变[first,last)的元素个数，有一些残余数据会留下来，如下图所示。情况类似remove算法。
4. unique算法可能产生一些残余数据，可以rease函数去除。注意， 如果result即为first， 便表示unique算法， 如果result不等于first, 便表示unique_copy算法。

unique有两个版本，因为所谓“相邻元素是否重复”可有不同的定义。第一版本使用简单的相等(equality)测试，第二版本使用一个Binary Predicate binary_pred做为测试做为测试准则，以下只列出第一版本的源代码，其中所有操作其实是借助unique_copy完成。

// 版本一
template<class ForwardIterator> 
ForwardIterator unique(ForwardIterator first, ForwardIterator last) {
first = adjacent_find(first, last); //首先找到相邻重复元素的起点
return unique_copy(first, last, first);//利用unique_copy完成
}

33.unique_copy

1. 算法 unique_copy可从[first,last）中将元素复制到以result开头 的区间上；如果面对相邻重复元素群， 只会复制其中第一个元素。 返回的迭代器指向以result开头的区间的尾端。
2. 与其它名为*_copy的算法一样，unique_copy 乃是unique的 一个复制式 版本， 所以它的特性与unique完全相同（请参考下图) , 只不过是将结果到另 一个区间而已。
3. unique_copy有两个版本，因为所谓“相邻元素是否重复”可有不同的定义。第一版本使用简单的相等(equality)测试，第二版本使用一个BinaryPredicate binary_pred作为测试准则。以下只列出第一版本的源代码。

//版本一
template <class InputIterator, class OutputIterator>
 inline Outputerator unique_copy(InputIterator first,InputIterator last,OutputIterator result){
 if (first == last} return result; 
//以下， 根据result的iterator category, 做不同的处理
return _unique_copy(first, last, result, iterator_category(result));
}

//版本－辅助函数，forward_iterator_tag版
template <Class InputIterator, class ForwardIterator>
ForwardIterator __unique_copy(InputIterator first,InputIterator last,ForwardIterator result,forward_iterator_tag){

*result = *first;//记录第一个元素
while (++first != last)//遍历整个区间
//以下， 元素不同， 就记录， 否则（元素相同）， 就跳过
if (*result != *first) *++result = *first; 
return ++result; 
}


//版本一辅助函数，Output_iterator_tag版
template<class InputIterator,class OutputIterator>
inline OutputIterator_unique_copy(InputIterator first,InputIterator last,OutputIterator result, Output_iterator_tag){
//以下，output iterator有一些功能限制，所以必须先知道其value type.
 return _unique_copy(first, last, result, value_type(first));
 }
//由于outputiterator为write only, 尤法像forwardIterator那般可以读取 
//所以不能有类似*result!= *first这样的判断操作，所以才需要设计这版本
//例如ostream_iterator就是个output iterator.
template <class InputIterator,class Outputiterator,class T> 
OutputIterator __unique_copy(Inputlterator first,InputIterator last,OutputIterator result, T*) {
// T为output Iterator的value type
T value= *first; 
*result=value;
while (++first != last)
if(value !=*first){
value = *first;
*++result = value;
}
return ++result;
}

接下来各小节(7.2~7.12)所介绍的算法，工作原理比较复杂。下面是各个 算法的运用实例：

#include
#include
#include
#include
using namespace std;

strcut even{//这是一个仿函数
bool operator()(int x)const
{return x%2 ? false :true;}
};

int main()
{
int ia[] = { 12,17,20,22,23,30,33,40 }; 
vector<int> iv(ia, ia+sizeof(ia)/sizeof(int));
cout<< *lower_bound(iv.begin(),iv.end(),21) <<endl;//22
cout<< *upper_bound(iv.begin(),iv.end(),21)<<endl;//22
cout<< *lower_bound(iv.begin(),iv.end(),22)<<endl;//22
cout<< *upper_bound(iv.begin(),iv.end(),22)<<endl;//23

//面对有序区间(sortedrange) , 可以二分查找法寻找某个元素
cout<<binary_search(iv.begin(), iv.end(),33) << endl; //1(true)
cout<<binary_search(iv.begin(), iv.end(),34) << endl; //0(false)
//下一个排列组合
next_permutation(iv.begin(), iv.end()); 
copy(iv.begin(), iv.end(), ostream_iterator<int>(cout, "")); 
cout << endl; 
// 12 17 20 22 23 30 40 33 

//上一个排列组合
prev_permutation(iv.begin(), iv.end()); 
copy(iv.begin(), iv.end(), ostream_iterator<int>(cout,＂＂));
cout<< endl; 
//12 17 20 22 23 30 33 40 

//随机重排
random_shuffle(iv.b egin(), iv.end()); 
copy(iv.begin(), iv.end(), ostream_iterator<int>(cout," ")); 
cout << endl; 
//33 12 30 20 17 23 22 40 

//将iv.begin()+4 - iv.begin()个元素排序，放进
// [iv.begin(), iv.begin()+4)区间内。剩余元素不保证维持原相对次序 
partial_sort(iv.begin(),iv.begin()+4, iv.end()); 
copy(iv.begin(), iv.end(), ostream_iterator<int>(cout, " ")); 
cout << endl; 
// 12 17 20 22 33 30 23 40 

//排序（缺省为递增排序）
sort(iv.begin(), iv.end()); 
copy(iv.begin(), iv.end(), ostream_iterator<int>(cout, " "));
cout << endl; 
// 12 17 20 22 23 30 33 40 

//排序（指定为递减排序）
sort(iv.begin(), iv.end(), greater<int>()); 
copy(iv.begin(), iv.end(), ostream_iterator<int>(cout,""));
cout << endl; 
// 40 33 30 23 22 20 17 12 

//在iv尾端附加新元素，使成为40 33 30 23 22 20 17 12 22 30 17
iv.push_back(22);
iv.push_back(30);
iv.push_back(17);


//排序，并保持“原相对位置”
stable_sort(iv.begin(),iv.end()); 
copy(iv.begin(), iv.end(), ostrearn_iterator<int>(cout," ")); 
cout << endl; 
// 12 17 17 20 22 22 23 30 30 33 40 


//面对一个有序区间，找出其中的一个子区间，其内每个元素都与某特定元素值相同； II返回该子区间的头尾迭代器
//如果没有这样的子区间，返回的头尾迭代器均指向该特定元素可插人
// (并仍保持排序）的地点
pair<vector<int>>::iterator,vector<int>::iterator>pairlte;
pairIte= equal_range(iv.begin(),iv.end(),22);
cout<<*(pairite.first)<< endl;//22(lower_bound)
cout<<*(pairite.second)<< endl;//23(upper_bound)
pairIte = equal_range(iv.begin(),iv.end(),25); 
cout << *(pairite.first)<< endl; //30(lower_bound)
cout << *(pairite.second) << endl;//30 (upper_bound)

random_shuffle (iv.begin() , iv.end()) ; 
copy(iv.begin(), iv.end(), ostrearn_iterator<int> (cout, " "));
cout<<endl; // 22 30 30 17 33 40 17 23 22 12 20 

//将小于*(iv.begin()+5)(本例为40)的元素置于该元素之左
//其余置于该元素之右。不保证维持原有的相对位置
nth_element(iv.begin(), iv.begin()+5,iv.end()); 
copy(iv.begin(), iv.end(), ostream_iterator<int>(cout, " ")); 
cout<<endl;// 20 12 22 17 17 22 23 30 30 33 40 

//将大于*(iv. begin() +5) (本例为22)的元素置于该元素之左
//其余置于该元素之右。不保证维待原有的相对位置
nth_element(iv.begin(), iv.begin()+5, iv.end(), greater<int>()); copy(iv.begin(), iv.end(), ostrearn_iterator<int>(cout, " ")); 
cout<<endl; // 40 33 30 30 23 22 17 17 22 12 20 

//以“是否符合even()条件”为依据，将符合者置于左段，不符合者置于右段
//保证维持原有的相对位置。如不需要“维持原有的相对位置”，可改用partiton()
stable_partition (iv. begin() , iv.end() , even()) ; 
copy(iv.begin(), iv.end(), ostream_iterator<int>(cout,"")); 
cout<<endl;// 40 30 30 22 22 12 20 33 23 17 17 
}

7.2 lower_bound(应用于有序区间）

1. 这是二分查找(binary search)的一种版本， 试图在已排序的[first,last)中寻找元素value。
2. 如果[first,last)具有与value相等的元素(s), 便返回 一个迭代器， 指向其中第一个元素。 如果没有这样的元素存在， 便返回 “假设这样的元素存在时应该出现的位置” 。
3. 也就是说， 它会返回 一个迭代器， 指向第一个 “不小于value"的元素。 如果value大于[first,last）内的任何一个元素， 则返回last 。
4. 以稍许不同的观点来看lower_bound, 其返回值是 “在不破坏排序状态的原则下， 可插人value的第一个位置” ，见下图。

这个算法有两个版本，版本一采用operator<进行比较，版本二采用仿函数 comp。更正式地说，版本一返回[first,last)中最远的迭代器i, 使得[first, i ) 中的每个迭代器j都满足 *j < value。 版本二返回[first. last ）中最远的迭代器i,使［first,i）中的每个迭代器j都满足 "comp(*j, value)为真” 。

//版本一
template <class ForwardIterator, class T> 
inline ForwardIterator lower_bound(ForwardIterator first,ForwardIterator last,const T& value){
return _lower_bound(first, last, value, distance_type(first),iterator_category(first);
}

//版本二
template <class ForwardIterator, class T, class Compare> 
inline ForwardIterator lower_bound(ForwardIterator first,ForwardIterator last,const T& value,Compare comp){
return _lower_bound(first, last, value, comp, distance_type(first), 
iterator_category(first));
}

下面是版本一的两个辅助函数。版本二的辅助函数极为类似，就不列出了。

//版本一的forward_iterator版本
template<class ForwardIterator,class T, class Distance> 
ForwardIterator __lower_bound(ForwardIteratorfirst, ForwardIterator last, const T& value, Distance*, forward_iterator_tag){
Distance len = O; 
distance(first,last,len); //求取整个区间的长度len
Distance half; 
ForwardIterator middle; 
while (len > 0) { 
half= len >> 1; //除以2
middle= first; //这两行令middle指向中间位置
advance(middle, half); 
if (*middle< value) {//如果中间位置的元素值＜标的值
first= middle; //这两行令first指向middle的下一位置
++first; 
len = len -half -1;//修正len,回头测试循环的结束条件
}
else
len = half;//修正len,回头测试循环的结束条件
}
return first;
}

//版本一的random_access_iterator版本
template <class RandomAccessIterator,class T, class Distance>
RandomAccessIterator __lower_bound(RandmAccessIterator first,RandmAccessIterator last,const T& value,Distance,random_Access_iterator_tag){
Distance len = last-first; //求取整个区间的长度len Distance half; 
RandomAccessIterator middle; 
while (len > 0) {
half= len >> 1; //除以2
middle= first+ half; //令middle指向中间位置(r-a-i才能如此）
if(*middle<value){//如果中间位置的元素值<目标值
first = middle +1;//令first指向middle的下一位置
len = len - half - 1;//修正len,回头测试循环的结束条件
}
else
len = half;
}
return first;
}

7.3 upper_bound(应用于有序区间）

1. 算法upper_bound是二分查找(binary search)法的一个版本。 它试图在已排序的[first,last)中寻找value。 更明确地说， 它会返回 ”在不破坏顺序的情况下，可插入value的最后一个合适位置”。见下图。
2. 由于STL规范，“区间圈定”时的起头和结尾并不对称（是的，[first,last)包含first但不包含last), 所以upper_bound与lower_bound的返回值意义大有不同。
3. 如果你查找某值，而它的确出现在区间之内，则lower_bound返回 的是一个指向该元素的迭代器。然而upper_bound不这么做。因为upper_bound所返回的是在不破坏排序状态的情况下，value可被插入的“最后一个“合适位置。如果value存在，那么它返回的迭代器将指向value的下一位置，而非指 向value本身。

upper_bound有两个版本，版本一采用operator<进行比较，版本二采用仿函数comp。更正式地说，版本一返回[first,last)区间内最远的迭代器i,使[first,i)内的每个迭代器）都满足"value< *j不为真＂。版本二返回[first,last)区间内最远的迭代器i,使[first，i)中的每个迭代器j都满足"comp(value, *j)不为真” 。

//版本一
template <class ForwardIterator, class T> 
inlirie ForwardIterator upper_bound(ForwardIterator first,ForwardIterator last,const T& Value){
return __upper_bound(first,last,value,distance_type(first),iterator_category(first);
}
//版本二
template <class ForwardIterator, class T, class Compare> 
inline ForwardIterator upper_bound(ForwardIterator first, ForwardIterator last,const T& value, Compare comp) { 
return _upper_bound(first, last, value, comp, distance_type(first),iterator_category(first));
}

下面是版本一的两个辅助函数。版本二的辅助函数极为类似，我就不列出了。

//版本一的forward_iterator版本
template <class ForwardIterator, class T, class Distance> 
ForwardIterator _upper_bound(ForwardIterator first,ForwardIterator last, const T& value, Distance*, forward_iterator_tag) { 
Distance len = O; 
distance(first,last,len);//求取整个区间的长度len
Distance half; 
ForwardIterator middle; 
while (len > 0) { 
half = len >> 1; //除以2
middle = first; //这两行令middle指向中间位置
advance(middle, half); 
if (value < *middle) //如果中间位置的元素值＞目标的值
len = half;//修正len, 回头测试循环的结束条件
else {
first = middle; //这两行令first指向middle的下一位置
++first; 
len = len - half - 1;//修正len, 回头测试循环的结束条件
}
}
return first;
}

//版本一的random_access_iterator版本
template<class RandomAccessIterator,class T, class Distance> 
RandomAccessIterator _upper_bound(RandomAccessIterator first, RandomAccessIterator last, const T& value, Distance*,
random_access_iterator_tag) {
Distance len = last -first;//求取整个区间的长度len
Distance half; 
RandomAccessIterator middle; 
while (len > 0) {
 half=len >> 1;//除以2
 middle = first+half;//令middle指向中间位置
 if (value < *middle) //如果中间位置的元素值＞目标值
len = half; //修正len,回头测试循环的结束条件
else { 
first= middle+ 1; //令fist指向middle的下一位置
len = len -half -1;//修正len,回头测试循环的结束条件
}
}
return first;
}

7.4 binary _search (应用千有序区间）

1. 算法binary_search是一种二分查找法，试图在已排序的［first,last)中 寻找元素value。如果[first,last)内有等同于value的元素，便返回true, 否则返回false。
2. 返回单纯的bool或许不能满足你，前面所介绍的lower_bound和 upper_bound能够提供额外的信息。事实上binary_search便是利用lower_bound先找出“假设value存在的话，应该出现的位置”，然后再对比该位置上的值是否为我们所要查找的目标，并返回对比结果。
3. binary_search的第一版本采用operator<进行比较，第二版本采用仿函数comp进行比较。

正式地说，当且仅当(if and only if) [first, last）中存在一个迭代器1使得"*i < value和value<*i皆不为真”，则第一版本返回true。当且仅当 在[first,last)中存在一个迭代器i使得"comp(*i,value)和comp(value, *i)皆不为真”，则第二版本返回true。

//版本一
template<class ForwardIterator, class T>
bool binary_search(ForwardIterator first, ForwardIterator last,const T& value){
ForwardIterator i = lower_bound(first,last,value);
return i !=last && !(value<*i);
}

//版本二
template<class ForwardIterator, class T, class Compare> 
bool binary_search(ForwardIterator first, ForwardIterator last,const T& value, Compare comp) { 
ForwardIterator i = lower_bound(first,last, value, comp); 
return i != last && !comp(value, *i); 
}

7.5 next_permutation

1. STL提供了两个用来计算排列组合关系的算法， 分别是next_permucation和prev_permutation。

2. 首先我们必须了解什么是 “下一个”排列组合，什么是 “前一个” 排列组合。 考虑三个字符所组成的序列{a,b,c}。 这个序列有六个可能的排 列组合： abc, acb, bac, bca, cab, cba。 这些排列组合根据less-than操作符 做字典顺序(lexicographical)的排序。

3. 也就是说， abc 名列第一，因为每一个元素都小于其后的元素。acb是次一个排列组合， 因为它是固定了a (序列内最小元 素）之后所做的新组合。

4. 同样道理， 那些固定b (序列内次小元素）而做的排列组 合，在次序上将先于那些固定c而做的排列组合。 以bac和bca为例，bac在bca 之前， 因为序列ac小于序列ca。

5. 面对bca, 我们可以说其前一个排列组合是 bac, 而其后一个排列组合是cab。 序列abc没有 “前一个”排列组合，cba没 有 “后一个” 排列组合。

6. next_permutation ()会取得[first,last）所标示之序列的下一个排列组 合。 如果没有下一个排列组合， 便返回false; 否则返回true。

7. 这个算法有两个版本。 版本一使用元素型别所提供的less-than操作符来决定 下一个排列组合， 版本二则是以仿函数comp来决定。

稍后即将出现的实现，简述如下，符号表示如下图所示。 首先，从最尾端开始往前寻找两个相邻元素，令第一元素为*i, 第二元素为*ii, 且满足 *i<*ii。 找到这样一组相邻元素后，再从最尾端开始往前检验，找出第一个大于*i的元素， 令为*j将i、j元素对调，再将ii之后的所有元素颠倒排列。此即所求之 “下 一个“ 排列组合。

next_permutation算法的实现细节符号表示:

举个实例，假设有序列{0,1,2,3,4},下图便是套用上述演算法则，一步一步获得的“下一个“排列组合。图中只框出那符合“第一元素为*i，第二元素为*ii,且满足*i< *ii"的相邻两元素，至于寻找适当的j、对调、逆转等操作并未显示出。

以下便是版本一的实现细节。版本二相当类似，就不列出来了。

//版本一
template<class BidirectionalIterator> 
bool next_permutation(BidirectionalIterator first,BidirectionalIterator last){
if (first == last) return false;//空区间
BidirectionalIterator i = first; 
++i;
if(i == last)return false;//只有一个元素
 i = last;//i指向尾端
 --i;
 for(;;){
 BidirectionalIterator ii=i;
 --i;
 //以上，锁定一组（两个）相邻元素
 if(*i<*ii)//如果前一个元素小于后一个元素
 BidirectionalIterator j = last;//令j指向尾端
while (!(*i < *--j)); //由尾端往前找，直到遇上比*i大的元索
iter_swap(i, j) ; //交换i,j
reverse(ii, last); //将ii之后的元素全部逆向重排
return true; 
}
if(i == first){//进行至最前面了
reverse(first,last);//全部逆向重排
return false;
  }
 }
}

7.6 prev _permutatlon

1. 所谓 “前一个排”列组合， 其意义已在上一节阐述。 实际做法简述如下， 其中所用的符号如（7.5）图所示。
2. 首先，从最尾端开始往前寻找两个相邻元素， 令第一元素为*i， 第二元素为*ii, 且满足 *i > *ii。
3. 找到这样一组相邻元素后， 再从 最尾端开始往前检验， 找出第一个小于*i的元素， 令为*j’,将 i, j元素对调， 再将ii之后的所有元素颠倒排列。 此即所求之 “ 前一个"排列组合。

举个实例，假设有序列 {4,3,2,1,0}, 下图便是套用上述演算法则，一步一步获得的“前一个"排列组合。图中只框出那符合“第一元素为*i,第二 元素为*ii,且满足*i> *ii,的相邻两元素，至于寻找适当的j、对调、逆转等操作并未显示出。

下面是版本一的实现细节，版本二非常类似，就不列出来了。

//版本一
template <class BidirectionalIterator>
bool prev_permutation(BidirectionalIterator first,BidirectionalIterator last){
if(first == last)return false;//空区间
BidirectionalIterator i =first;
++i;
if(i == last)return false;//只有一个元素 
i = last;//i指向尾端
--i;

for(;;){
BidirectionalIterator ii =i;
--i;
//以上，锁定一组（两个）相邻元素
if(*ii < *i){//如果前一个元素大于后一个元素
BidirectionalIterator j = last;//令j指向尾端
while (!(*--j < *i));//由尾端往前找，直到遇上比*i小的元素
iter_swap(i, j) ; //交换i,j 
reverse(ii, last);//将ii之后的元素全部逆向重排
return true; 
}
if(i==first){//进行至最前面了
reverse(first,last);//全部逆向重排
return false;
  }
 }
}

7.7 random_shuffle

1. 这个算法将[first,last)的元素次序随机重排。也就是说，在N!种可能的元素排列顺序中随机选中一种，此处N为last-first。
2. N个元素的序列，其排列方式有N!种，random_shuffle会产生一个均匀分布，因此任何一个排列被选中的机率为1/N!。这很重要，因为有不少算法在其第一阶段过程中必须获得序列的随机重排，但如果其结果未能形成“在N!个可能 排列上均匀分布(uniformdistribution) " , 便很容易造成算法的错误。
3. random_shuffle有两个版本， 差别在于随机数的取得。 版本一使用内部随机 数产生器，版本二使用一个会产生随机随机数的仿函数。
   4.特别请你注意， 该仿函数 的传递方式是by reference而非一般的by value, 这是因为随机随机数产生器有一 个重要特质： 它拥有局部状态(local state) , 每次被调用时都会有所改变， 并因此保障产生出来的随机数能够随机。

下面是SGI版的实现细节：

//SGI版本 一
template <class RandomAccessIterator>
inline void random_shuffle(RandomAccessIterator first,RandomAccessIterator last) {
__random_shuffle(first,last,distance_type(first));
}

template <class RandornAccessIterator, class Distance> 
void random_shuffle(RandornAccessIterator first, RandornAccessIterator last,Distance*) { 
if (first == last) return;
for (RandornAccessIterator 1 =first + 1; i != last; ++i) 
#ifdef _STL_NO_DRAND48 
iter_swap(i,first+ Distance(rand()%((i - first) + 1))); 
#else 
iter_swap(i,first+ Distance(lrand48()%((i - first) + 1))); 
#endif 
//注意， 在GCC2.91.57中，_STL_NO_DRAND48是未定义的， 因此上述实现代码
//会采用lrand48 ()那个版本。 但编译时却又说lrand48 () undeclared 
}
//SGI版本二
template <class RandornAccessIterator, class RandomNumberGenerator> 
void random_shuffle(RandornAccessIterator first, RandornAccessIterator last,RandomNumberGenerator& rand){ //注意，by·reference
if(first == last) return;
for(RandornAccessIterator i = first+ 1; i != last; ++i) 
iter_swap(i, first + rand((i - first) + 1));
}

奇怪的是，GCC2.91-for-win并未定义_STL_NO_DRAND48 (见 1.8.3节的组态测试），因此对random_shuffle的调用会流向上述的lrand48()版 本，然而联结时却又说lrand48()未曾声明。 例如，以下程序可通过C++Builder4 和VC6, 却无法通过GCC2.91-for-win:

int main()
{
	vector<int>vec;
	for(int ix=0;ix<10;ix++)
	vec.push_back(ix);

	random_shuffle( vec.begin(), vec.end()) ; 
	copy(vec.begin(), vec.end(), ostrearn_iterator<int>(cout," ")) ; 
	// 	6 8 9 2 1 4 3 7 0 5 
	return 0; 
	}

为此，我特别把RaugeWaveSTL对random_shuffle()的实现细节列出于下：

// RW版本一。in 
template <class RandomAccesslterator> 
inline void random_shuffle(RandomAccessiterator first,RandomAccesslterator last)
{
__random_shuffle(first,last,__distance_type(first));
}

// RW版本一.in 
template<class RandomAccessIterator, class Distance>
void __random_shuffle(RandomAccessIterator first,RandomAccessIterator last, Distance*) 
{
if (!(first == last))
for (RandomAccessIterator i = first+1; i ! = last;++i)
iter_swap(i,first+ Distance(__RWSTD::_long_random((i-first)+1))); 
//上述_RWSTD::_long_random是内部的随机数产生器
}
// RW版本二in  
template<class RandomAccessIterator, class RandomNumberGenerator>
 void random_shuff1e(RandomAccessIterator first, RandomAccessIterator last,RandornNumberGenerator& rand)
 {
 if(!(first == last))
 for (RandornAccessIterator i =first+ 1; i != last; ++i)
 iter_swap(i, first+rand((i -first)+ 1));
 }

7.8 partial_sort / partial_sort_copy

1. 本算法接受一个middle迭代器（位于序列［first,last)之内），然后重新安排[first,last),使序列中的middle-first个最小元素以递增顺序排序， 置于［first,middle)内。其余last-middle个元素安置于[middle,last)中， 不保证有任何特定顺序。
2. 使用sort算法，同样能够保证较小的N个元素以递增顺序于[first,first+N)之内。选择partial_sort而非sort的唯一理由是效率。是 的，如果只是挑出前N个最小元素来排序，当然比对整个序列排序快上许多。
3. partial_sort有两个版本，其差别在于如何定义某个元素小于另元素。第一版本使用less-than操作符，第二版本使用仿函数comp。算法内部采用heapsort来完成任务。简述如下：

• partial_sort的任务是找出middle-first个最小元素，因此，首先界定出区间[first,middle), 并利用4.7.2节的make_heap()将它组织成一个max-heap, 然后就可以将[middle,last)中的每一个元素拿来与max-heap的最大值比较(max-heap的最大值就在第一个元素身上，轻松可以获得如果小于该最大值，就互换位置并重新保持max-heap的状态。
  • 如此一来，当我们走遍整个[middle,last)时，较大的元素都已经被抽离出[first，middle),这时候再以 sort_heap()将[first,middle)做一次排序，即功德圆满见下图的步骤详解。
    
    下面是 partial_sort 的实现细节。 考虑到篇幅， 我只列出第一版本，注意， partial_sort 只接受 RandomAccesslterator,

//版本一
template <class RandomAccessiterator> 
inline void partial_sort(RandomAccessIterator first,RandomAccessIterator middle,RandomAccessIterator last) { 
__partial_sort(first,middle,last,value_type(first));
}

template <class RandomAccessIterator, class T>
void __partial_sort(RandomAccessIterator first,RandomAccessIterator middle,RandomAccessIterator last,T*){
make_heap(first,middle);
//注意，以下的i
 for (RandomAccessIterator i = middle; i < last; ++i)
 if(*i<*first)
 __pop_heap(first,middle,i,T(*i),distance_type(first));
 sort_heap(first,middle);
 }

partial_sort有一个姊妹，就是partial_sort_copy:
//版本一
template<class InputIterator,class RandomAccessIterator>
inline RandomAccessIterator
partial_sort_copy(InputIterator first,InputIterator last,RandomAccessIterator result_first, RandomAccessIterator result_last);

//版本二
template <class InputIterator, class RandomAccessIterator,
class Compare> 
inline RandomAccessIterator
partial_sort_copy(Input Iterator first,InputIterator last, RandomAccessIterator result_first, RandomAccessIterator resu1t_1ast, compare comp);

partial_sort和partial_sort_copy两者行为逻辑完全相同，只不过后 者将(last-first)个最小元素（或最大元素，视comp而定）排序后的所得结果置于[result_first，result_last)。下面是运用实例：

int ia[12] = {69,23,80,42,17,15,26,51,19,12,35,8 }; 
vector<int> vec(ia, ia+12); 
ostream_iterator<int> oite(cout," ");  
partial_sort(vec.begin(), vec.begin()+7, vec.end()); 
copy(vec.begin(), vec.end(), oite); cout << endl; 
// 8 12 15 17 19 23 26 80 69 51 42 35 
vector<int> res(7); 
partial_sort_copy(vec.begin(), vec.begin()+7, res.begin(),res.end(),greater<int>());
copy(res.begin(), res.end(), oite); cout << endl;// 26 23 19 17 15 12 8 

7.9 sort

1. STL所提供的各式各样算法中，sort()是最复杂最庞大的一个。这个算法接受两个RandomAccesslterators(随机存取迭代器），然后将区间内的所有元素以渐增方式由小到大重新排列。
2. 第二个版本则允许用户指定一个仿函数(functor) 作为排序标准(以operator<作为排序比较标准）STL的所有关系型容器(associative containers)都拥有自动排序功能（底层结构采用RB-tree,见第5章），所以不需要用到这个sort算法。
3. 至于序列式容器(sequence containers)中的stack、queue和priority-queue都有特别的出入口，不允许用户对元素排序。
4. 剩下vector、deque和list,前两者的迭 代器属于RandomAccesslterators,适合使用sort算法，list的迭代器则属于 Bidirectioinallterators, 不在STL标准之列的slist , 其迭代器更属于 Forwardlterators, 都不适合使用sort算法。
5. 如果要对list或slist排序，应该 使用它们自己提供的member functions sort ()。稍后我们便可看到为什么泛型算法sort（）一定要求RandomAccessIterators。

排序有多么重要

• 人类生活在一个有序的世界中。没有排序，很多事情无法进行。排过序的数据， 特别容易查找。电话簿总是以人名为键值来排序，对人名而言，电话簿是有序的， 对电话号码而言，电话簿是无序的。在电话簿里找一个人（从而得到他的电话号码） 很容易，但你能想象在电话簿里头不通过人名直接查找某个特定的电话号码吗？
  • 这类情况大量发生在日常生活中。字典需要排序，书籍索引需要排序，磁盘目录需要排序，名片需要排序，图书馆藏需要排序，户籍数据需要排序。任何数据只 要你想快速查找，就需要排序。
    • 犹有进者，排序可能使其它工作更快更轻松。如果你要确定（或找出）一堆数 据里头有没有重复的元素，先排序一遍再找，会比闷着头两两对比快得多。换句话 说，许多算法可能因为数据先行排序过而大幅改善效率。排序的成本，成为影响执 行时间的关键因素。

STL的sort算法，数据量大时采用QuickSort, 分段递归排序。一旦分段后的数据最小于某个门槛，为避免QuickSort的递归调用带来过大的额外负荷(overhead) , 就改用InsertionSort。如果递归层次过深，还会改用HeapSort (已 于4.7.2节介绍）。

以下分别介绍Quick Sort和Insertion Sort, 然后再整合起来介 绍STLsort算法。

①.Insertion Sort

1. Insertion Sort以双层循环的形式进行。
2. 外循环遍历整个序列，每次迭代决定出一个子区间；内循环遍历子区间，将子区间内的每一个“逆转对(inversion)倒转过来。
3. 所谓“逆转对”是指任何两个迭代器i,j,i< j而*i > *j。一旦 不存在“逆转对“，序列即排序完毕。
4. 这个算法的复杂度为O(N²),说起来并不理想，但是当数据量很少时，却有不错的效果，原因是实现上有一些技巧（稍后源代 码可见），而且不像其它较为复杂的排序算法有着诸如递归调用等操作带来的额外 负荷。下图是Insertion Sort的详细步骤示意。

SGI STL的Insertion Sort有两个版本，版本一使用以渐增方式排序，也就是说，以operator<为两元素的比较函数。版本二允许用户指定一个仿函数(functor) 作为两元素的比较函数。以下只列出版本一的源代码。由于STL规格并不开放 Insertion Sort, 所以SGI将以下函数的名称都加上双下划线，表示内部使用。

//版本一
template <class RandomAccessIterator>
void __insertion_sort(RandomAccessIterator first,RandomAccessiterator last) {
if(first == last)return;
for(RandomAccessIterator i = first+1; i !=last;++i)//外循环
__linear_insert(first,i, value_type(first));
 //以上,[first,i)形成一个子区间
 }

//版本－辅助函数
template <class RandomAccessIterator, class T>
inline void __linear_insert(RandomAccessIterator first,RandomAccessIterator last,T*){
T value = *last;//记录尾元素
if(value<*fisrt){//尾比头还小（注意，头端必为最小元素）
//那么就别个个比较了，一次做完爽快些...
copy_backward(first, last, last+ 1); //将整个区间向右递移一个位置
 *first= value;//令头元素等于原先的尾元素值
 }
 else//尾不小于头
 __unguarded_linear_insert(last,value);
 }
//版本一辅助函数
template<class RandomAccessIterator,class T>
void __unguarded_linear_insert(RandomAccessIterator last,T value){
RandomAccessIterator next = last; 
--next;
// insertion sort的内循环
//注意，一旦不再出现逆转对(inversion), 循环就可以结束了
while (value < *next) { //逆转对(inversion)存在
*last = *next; //调整
last = next; //调整迭代器 
--next; // 左移一个位置
}
*last = value;//value的正确落脚处
}

1. 上述函数之所以命名为unguarded_x是因为， 一般的Insertion Sort在内循 环原本需要做两次判断， 判断是否相邻两元素是 “逆转对“ ，同时也判断循环的 行进是否超过边界。
2. 但由于上述所示的源代码会导致最小值必然在内循环子区间的 最边缘， 所以两个判断可合为一个判断，所以称为unguarded_。
3. 省下一个判断操作， 乍见之下无足轻重，但是在大数据量的情况下，影响还是可观的，毕竟这是一 个非常根本的算法核心， 在大数据量的情况， 执行次数非常惊人。

稍后即将出场的几个函数， 也有以unguarded_为前缀命名者， 同样是因为 在特定条件下， 边界条件的检验可以省略（或说已融入特定条件之内）。

②.Quick Sort

• 拿Insertion Sort来处理大量数据，其O(N²)的复杂度就令人摇头了。 大数据量的情况下有许多更好的排序算法可供选择。

  • 正如其名称所昭示，Quick Sort 是目前已知最快的排序法， 平均复杂度为O(N log N), 最坏情况下将达O(N²）。

    • 不过lntroSort (极类似median-of-three QuickSort的 一种排序算法）可将最坏情况推 进到O(N log N)。 早期的STL sort算法都采用Quick Sort, SGI STL已改用lntroSort.。

Quick Sort算法可以叙述如下。 假设S代表将被处理的序列：

1. 如果S的元素个数为0或1, 结束。
2. 取S中的任何一个元素， 当作枢轴(pivot) v。
3. 将S分割为L, R两段， 使L内的每一个元素都小于或等于v, R内的每一个 元素都大于或等于v。
4. 对L,R递归执行Quick Sort。

Quick Sort的精神在于将大区间分割为小区间，分段排序。每一个小区间排序
完成后，串接起来的大区间也就完成了排序。最坏的情况发生在分割(partitioning)时产生出 一个空的子区间那完全没有达到分割的预期效果。下图说明了Quick Sort的分段排序。

注：Quick Sort采行分段排序。 分段的原则通常采用median-of-three (首、尾、 中央的中间值）。 因此，图中第一列以2为枢轴，分割出第二列所示的左右两 段 第二列的右段再以 16 为枢轴， 分割出第三列的两段。 依此类推。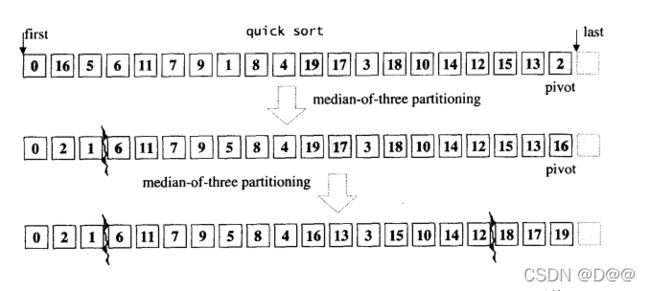

③.Median-of-Three (三点中值）

1. 注意，任何一个元素都可以被选来当作枢轴(pivot) , 但是其合适与否却会影响Quick Sort的效率。
2. 为了避免 “元素当初输入时不够随机” 所带来的恶化效应， 最理想最稳当的方式就是取整个序列的头、 尾、 中央三个位置的元素， 以其中值(median)作为枢轴。 这种做法称为 median-of-three partitioning , 或称为 mediun-of-three-QuickSort。
3. 为了能够快速取出中央位置的元素，显然迭代器必须能够随机定位，亦即必须是个RandomAccesslterators。

以下是SGI STL提供的三点中值决定函数：

//返回a,b,c之居中者
template <class T>
inline const T& _median(const T& a, const T& b, const T& c){
if(a<B)
if(b<c)//a
return b;
else if(a<c)//a=c,a
return c;
else
return a; 
else if (a < c) // c >a>= b 
return a; 
else if (b < c) //a>= b, a>= c, b < c
return c; 
else 
return b;
}

④.Partitioining (分割）

1. 分割方法不只一种， 以下叙述既简单又有良好成效的做法。 令头端迭代器first向尾部移动， 尾端迭代器last向头部移动。
2. 当＊first大于或等于枢轴时就停下来， 当*last小于或等于枢轴时也停下来，然后检验两个迭代器是否交错。
3. 如果first仍然在左而last仍然在右， 就将两者元素互换， 然后各自调整 个位置（向中央逼近）， 再继续进行相同的行为。
4. 如果发现两个迭代器交错了（亦即!(first< last)) , 表示整个序列已经调整完毕，以此时的first为轴，将 序列分为左右两半，左半部所有元素值都小于或等于枢轴，右半部所有元素值都大于或等于枢轴。

下面是SOISTL提供的分割函数， 其返回值是为分割后的右段第一个位置:

//版本
template <class RandomAccessIterator, class T> 
RandomAccessIterator __unguarded__partition( RandomAccessIterator first, RandomAccessIterator last, T pivot) { 
while(true){
while (*first < pivot) ++first; //first找到>= pivot的元素就停下来
--last; //调整
while (pivot<*last)--last;// last找到<=pivot的元素就停下来 
//注意，以下first
if (!(first<last)) return first;//交错， 结束循环
 iter_swap(first, last); //大小值交换
++first;//调整
}
}

下图是两个分割实例的完整过程，请参照以上源代码操作。

⑤.threshold (阀值）

• 面对一个只有十来个元素的小型序列，使用像Quick Sort这样复杂而（可能） 需要大量运算的排序法，是否划算？不，不划算，在小数据量的情况下，甚至简单如Insertion Sort者也可能快过Quick Sort，因为Quick Sort会为了极小的子序 列而产生许多的函数递归调用。
  • 鉴于这种情况，适度评估序列的大小，然后决定采用Quick Sort或Insertion Sort, 是值得采纳的一种优化措施。然而究竟多小的序列才应该断然改用Insertion Sort 呢？并无定论，5~20都可能导致差不多的结果，实际的最佳值因设备而异。

⑥.final insertion sort

优化措施永不嫌多，只要我们不是贸然行事(Donald Knuth说过一件名言： 贸然实施优化，是所有恶果的根源，premature optimization is the root of all evil)。 如果令某个大小以下的序列滞留在“几近排序但尚未完成＂的状态，最后再 以一次Insertion Sort将所有这些“几近排序但尚未竟全功”的子序列做一次完整的排序，其效率一般认为会比将所有子序列彻底排序”更好。这是因为Insertion Sort在面对“几近排序”的序列时，有很好的表现。

⑦.introsort

不当的枢轴选择，导致不当的分割，导致Quick Sort恶化为O(N²)。DavidR.
Musser (此君于STL领域大大有名）于1996年提出一种混合式排序算法：
Introspective Sorting (内省式排序, 简称lntroSort,其行为在大部分情况下几
乎与median-of-3 Quick Sort完全相同（当然也就一样快）。但是当分割行为
(partitioning)有恶化为二次行为的倾向时，能够自我侦测，转而改用Heap Sort, 使效率维持在Heap Sort的O(N log N),又比一开始就使用Heap Sort来得好。稍 后便可看到SGI STL源代码中对lntroSort的实现。

⑧.SGI STL sort

下面是SGI STL sort ()源代码：

//版本一
//千万注意： sort ()只适用于RandornAccessIterator
template <class RandornAccessIterator> 
inline void sort(RandornAccessIterator first,RandornAccessIterator last) {
if (first!= last){
__introsort_loop(first, last, value_type(first), _1g(last-first)*2); 
__final_insertion_sort(first, last); 
}
}

其中的_lg()用来控制分割恶化的情况：

//找出2^k <= n的最大值K。 例： n=7, 得k=2, n=20, 得k=4, n=8, 得k=3 
template <class Size> 
inline Size _lg(Size n) { 
Size k; 
for (k = O; n > 1; n >>= 1) ++k; 
return k; 
}

当元素个数为40时，_introsoft_loop ()的最后一个参数是5*2，意思是最多允许分割10层。lntroSort算法如下：

//版本一
//注意， 本函数内的许多迭代器运算操作， 都只适用于RandornAccess Iterators
 template <class RandornAccessIterator, class T, class Size> 
 void __introsort_loop(RandornAccessIterator first,RandornAccessIterator last, T*,Size depth_limit){
 //以下，_stl_threshold是个全局常数， 稍早定义为const int 16
 while(last - first>__stl_threshold){// >16
 if(depth_limit ==0){//至此， 分割恶化
 partial_sort(first, last, last); //改用heapsort
 return; 
 }
--depth_limit; 
//以下是median-of-3 partition, 选择一个够好的枢轴并决定分割点
//分割点将落在迭代器cut身上
RandornAccessIterator cut=__unguarded_partition(first,last,T(__median(*first,* (first + (last - first)/2) , *(last- 1)))) ;
//对右半段递归进行sort.
__introsort_loop(cut, last, value_type(first), depth_limit);
last = cut;
//现在回到while循环，准备对左半段递归进行sort
//这种写法可读性较差，效率并没有比较好
// RW STL采用一般教科书写法（直观地对左半段和右半段递归），较易阅读
}
}

1. 函数一开始就判断序列大小。_stl_threshold是个全局整型常数，定义如下： const int _stl_threshold= 16;

2. 通过元素个数检验之后，再检查分割层次。如果分割层次超过指定值（已在 前一段文字中对此做了说明），就改用partial_sort(),应该还记得先前介绍过的partial_sort()是以HeapSort完成的。

3. 通过了这些检验之后，便进入与Quick Sort完全相同的程序：以median-of-3方法确定枢轴位置， 然后调用_unguarded_partition()找出分割点（其源代码已于先前显示过），然后针对左右段落递归进行lntroSort。

当__introsort_loop()结束,[first,last)内有多个“元素个数少于 16"的子序列，每个子序列都有相当程度的排序，但尚未完全排序（因为元素个数 一旦小于_stl_threshold,就被中止进一步的排序操作了）。回到母函数 sort()，再进入_final_insertion_sort():

//版本一
template<class RandornAccessIterator>
void __final_insertion_sort(RandornAccessIterator first,RandornAccessIterator last) { 
if (last-first > stl_threshold) { //> 16
__insertion_sort(first, first+__stl_threshold) ; 
__unguarded_insertion_sort(first + __stl_threshold, last);
}
else
__insertion_sort(first,last);
}

此函数首先判断元素个数是否大于16。 如果答案为否， 就调用 _insertion_sort ()加以处理。 如果答案为是，就将[first, last)分割为长度16的一段子序列， 和另一段剩余子序列， 再针对两个子序列分别调用 _insertion_sort()和_unguarded_insertion_sort()。 前者源代码已于先 前展示过， 后者源代码如下：

//版本一
template<class RandomAccessIterator>
inline void __unguarded_insertion_sort(RandomAccessIterator first,RandomAccessIterator last) {
__unguarded_insertion_sort_aux(first, last, value_type(first));
}

//版本一
template <class RandomAccessIterator, class T> 
void __unguarded_insertion_sort_aux(RandomAccessIterator first,RandomAccessIterator last,T*)[
for (RandomAccessIterator i = first; i!=last;++i)
__unguarded_linear_insert(i,T(*i));//见先前展示
}

这就是SGI STL sort算法的精彩故事。为了做个比较，我再列出RW STL sort ()的部分（主要是上层）源代码。RW版本用的是纯粹是Quick Sort, 不是 lntroSort。

template <class RandomAccessIterator>
inline void sort (RandomAccessIterator first,RandomAccessIterator last){
__quick_sort_loop(first, last); 
__final_insertion_sort(first, last);//其内操作与SGI STL完全相同
}
}
template <class RandomAccessIterator> 
inline void __quick_sort_loop(RandomAccessIterator first,RandomAccessIterator last)
{
__quick_sort_loop_aux(first, last,_RWSTD_VALUE_TYPE(first));
}
template<class RandornAccessIterator,class T> 
void __quick_sort_loop_aux (RandomAccessIterator first,RandornAccessTterator last, 
T*) {
while (last -first>__stl_threshold)
{
// rnedian-of-3 partitioning

RandomAccessIterator cut = __unguarded_partition(first,last,T(__median(*first,*(first+(last-first)/2),*(last-1)));
if(cut - fist >= last - cut)
{
__quick_sort_loop(cut,last);//对右段递归处理
last = cut;
}
else
{
__quick_sort_loop(first,cut);//对左段递归处理
first = cut;
}
 }
}

7.10 equal_range (应用于有序区间）

1. 算法equal_range是二分查找法的一个版本，试图在已排序的［first,last)中寻找value。它返回一对迭代器i和j,其中i是在不破坏次序的前提下，value 可插入的第一个位置（亦即lower_bound), j则是在不破坏次序的前提下，value 可插入的最后一个位置（亦即upper_bound)。
   因此，[i,j)内的每个元素都等同于value,而且[i,j)是［first，last)之中符合此一性质的最大子区间。
2. 如果以稍许不同的角度来思考equal_range, 我们可把它想成是 [first,last）内”与value等同”之所有元素所形成的区间A。由于 [first,last）有序(sorted), 所以我们知道”与value等同”之所有元素一定都相邻。于是，算法lower_bound返回区间A的第一个迭代器，算法upper_bound返回区间A的最后元素的下一位置，算法equal_range则是以pair 的形式将两者都返回。
3. 如果以稍许不同的角度来思考equal_range, 我们可把它想成是 [first,last）内”与value等同”之所有元素所形成的区间A。由于 [first,last）有序(sorted), 所以我们知道”与value等同”之所有元素一定都相邻。于是，算法lower_bound返回区间A的第一个迭代器，算法upper_bound返回区间A的最后元素的下一位置，算法equal_range则是以pair 的形式将两者都返回。

本算法有两个版本，第一版本采用operator<进行比较，第二版本采用仿函数comp进行比较。稍后只列出版本一的源代码。下图展示equal_range的意义。

//版本一
template<class ForwardIterator,class T> 
inline pair<ForwardiIerator, ForwardIterator> 
equal_range(ForwardIterator first, Forwarditerator last,const T& value) { 
//根据迭代器的种类型(category), 采用不同的策略
return _equal_range(first, last, value, distance_type(first),iterator_category(first));
}
//版本一的random_access_iterator版本
template<classRandomAccessIterator,class T, class Distance> 
pair<RandomAccessIterator,RandomAccessIterator>
__equal_range(RandomAccessIterator first,RandomAccessIterator last,const T& value, Distance*, random_access_iterator_tag){
 Distance len = last-first; 
Distance half; 
RandomAccessIterator middle, left, right; 
while (len > 0) {//整个区间尚未遍历完毕
half= len >> 1; //找出中央位置
middle= first+half; //设定中央迭代器
if (*middle< value) {//如果中央元素＜指定值
first= middle+ 1; //将运作区间缩小（移至后半段），以提高效率
len = len -half -1;
}else if (value< *middle)//如果中央元素＞指定值
len = half;//将运作区间缩小（移至前半段）以提高效率
else{//如果中央元素＝＝指定值
//在前半段找lower_bound
left= lower_bound(first, middle, value); 
//在后半段找lower_bound
right= upper_bound(++middle, first + len, value); 
return pair<RandomAccessIterator,RandomAccessIterator>(left,right);
}
}
整个区间内都没有匹配的值，那么应该返回一对迭代器，指向第一个大于value的元素
return pair<RandomAccessIterator, RandomAccessIerator>(first,first);
}
//版本一的forward_iterator版本
template <class ForwardIterator,class T, class Distance> pair<ForwardIterator, ForwardIterator> 

__equal_range(ForwardIterator first, ForwardIterator last, canst T& value, Distance*,forward_iterator_tag) { 
Distance len = 0; 
distance(first, last,len);
Distance half; 
ForwardIterator middle, left, right;
while (len > 0) { 
half= len >> 1; 
middle = first; //此行及下一行，相当于RandornAccessIterator的
advance(middle, half); // middle= first + half;
 if (*middle < value) { 
 first= middle; //此行及下一行，相当千RandornAccessItcrator的
 ++first;//first =middle+ 1; 
len = len -half-1;
}
else if(value < *middle)
len half;
else{
left=lower_bound(first,middle,value}; 
//以下这行相当于RandomAccessIterator的first+=len; 
advance (first, len); 
right=upper_bound(++middle, first, value); 
return pair<ForwardIterator,ForwardIterator>(left,right);
}
}
return pair<ForwardIterator, ForwardQIterator>(first,first);
}

7.11 inplace_merge (应用于有序区间）

1. 如果两个连接在一起的序列[first,middle)和[middle,last)都已排 序，那么inplace_merge可将它们结合成单一一个序列，并仍保有序性(sorted)。 如果原先两个序列是递增排序，执行结果也会是递增排序，如果原先两个序列是递 减排序，执行结果也会是递减排序。
2. 和merge一样，inplace_merge也是种稳定(stable)操作。每个作为数据来源的子序列中的元素相对次序都不会变动；如果两个子序列有等同的元素，第一序列的元素会被排在第二序列元素之前。

inplace_merge有两个版本，其差别在于如何定义某元素小于另个元素。第一版本使用operator<进行比较，第二版本使用仿函数(functor) comp进行比较。以下列出版本的源代码：

template <Class BidirectionalIterator>
inline void inplace_merge(BidirectionalIterator first,BidirectionalIterator middle, BidirectionalIterator last) {
//只要有任何一个序列为空，就什么都不必做
if(first== middle || middle == last) return; 
__inplace_merge_aux(first, middle, last, value_type(first),distance_type(first));
}

//辅助函数
template<class BidirectionalIterator, class T, class Distance> 
inline void inplace_merge_aux(BidirectionalIterator first,BidirectionalIterator middle, BidirectionalIterator last, T*, Distance*) { 
Distance len1 = O; 
distance(first,middle,len1); //len1表示序列一的长度
Distance len2 = O; 
distance(middle,last,len2);//len2表示序列二的长度
//注意，本算法会使用额外的内存空间（暂时缓冲区）
temporary_buffer<BidirectionalIterator, T> buf(first,last);
if (buf.begin() == 0) //内存配置失败
__merge_without_buffer(first, middle, last, len1, len2); else //在有暂时缓冲区的情况下进行
__merge_adaptive(first,middle, last, len1, len2,buf.begin(),Distance(buf.size()));
}

这个算法如果有额外的内存（缓冲区）辅助，效率会好许多。但是在没有缓冲 区或缓冲区不足的情况下，也可以运作。为了篇幅，也为了简化讨论，以下我只关注有缓冲区的情况。

//辅助函数。有缓冲区的情况下
template<class BidirectionalIterator,class Distance, class Pointer> void __merg_adaptive(BidirectionalIterator first, BidirectionalIterator middle, 
BidirectionalIteratorb last, 
Distance len1, Distance len2, 
Pointer buffer, Distance buffer_size) {
if (len1 <= len2 && len1 <= buffer_size){
 //ease1. 缓冲区足够安置序列一
Pointer end_buffer = copy(first, middle, buffer);
merge(buffer, end_buffer, middle, last,first);
}
else{// case3. 缓冲区空间不足安置任何一个序列

BidirectionalIterator first_cut = first; Bidirectionaliterator second_cut = middle;
Distance len11 = O; 
Distance len22 = O; 
if (len1 > len2) { //序列一比较长
len11 = len1 / 2; 
advance(first_cut, len11); 
second_cut=lower_bound(middle, last, *first_cut);
distance(middle,second_cut, len22); 
}
else{//序列二比较长
len22 = len2/2; //计算序列二的一半长度
advance(second_cut, len22); 
first_cut=upper_bound(first, middle, *second_cut); 
distance(first, first_cut, len11); 
}
BidirectionalIterator new_middle=__rotate_adaptive(first_cut,middle, second_cut，len1-len11,len22, buffer, buffer_size); 
//针对左段，递归调用
__merge_adaptive(first,first_cut, new_middle, len11, len22, buffer, buffer_size); 
//针对右段，递归调用
__merge_adaprtive(new_middle,second_cut, last, len1 -len11,len2 -len22, buffer, buffer_size);
}
}

上述辅助函数首先判断缓冲区是否足以容纳inplace_merge所接受的两个序列中的任何一个。如果空间充裕（源代码中标示ease1和case2之处），工作逻辑很简单：把两个序列中的某一个copy到缓冲区中，再使用merge完成其余工 作是的，merge足堪胜任，它的功能就是将两个有序但分离(sorted and separated) 的区间合并，形成一个有序区间，因此，我们只需将merge的结果置放处（迭代器result)指定inplace_merge所接受之序列起始点（迭代器first)即可。

下图是一份实例及说明：

当缓冲区足够容纳［first,middle),就将[first,middle]复制到缓冲区，再以merge将缓冲区和第二序列[middle,last）合并。

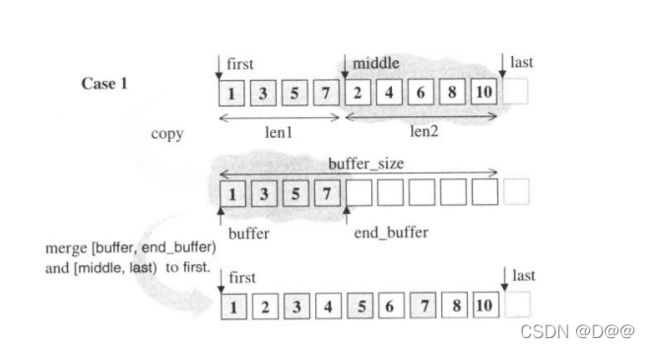
当缓冲区足够容纳[middle, last) , 就将[middle,last)复制到 缓冲区，再以_merge_backward将第二序列[first,middle)和缓冲区和合并。:

但是当缓冲区不足以容纳任何一 个序列时（源代码中标示case3之处），情况 就棘手多了。面对这种情况，我们的处理原则是，以递归分割(recursive partitioning) 的方式，让处理长度减半，看看能否容纳于缓冲区中（如果能，才好办事儿）。例如，沿用上图的输入状态，并假设缓冲区大小为3, 小于序列 的长度4和序二的长度5, 于是，拿较长的序列二开刀，计算出first_cut和second_cut如 下：

BidirectionalIterator first_cut= first;
BidirectionalIterator second_cut= middle;
Distance len11 = 0; 
Distance len22 = 0; 

现在可以分段处理了。 首先针对左段[first, first_cut, new_middle), 也就是上图的淡蓝色阴影部分{ 1,3,5,2,4} , 做递归调用：

//针对左段， 递归调用
__merge_adaptive(first, first_cut, new_middle, 
len11, len22, buffer, buffer_size); 

由于本例的缓冲区（大小3)此时巳显足够， 所以轻松获得这样的结果：

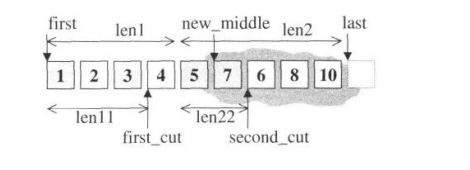
再针对右段[new_middle,second_cut, last), 也就是上图的淡蓝色阴影部 分{7,6,8,10}, 做递归调用：

//针对右段， 递归调用
__merge_adaptive(new_rniddle, second_cut, last,len1 - len11, len2 - len22,buffer, buffer_size); 

由于本例的缓冲区（大小3)此时已显足够， 所以轻松获得这样的结果：

通过这样的实例步进程序，相信你对于inplace_merge的操作已有了一个相 当程度的概念。

7.12 nth_element

这个算法会重新排列[first,last），使迭代器nth所指的元素，与“整个[first, last)完整排序后，同一位置的元素”同值。此外并保证[nth,last)内没有任何一个元素小于（更精确地说是不大于）[first，nth)内的元素，但对于 [first, nth)和[nth,last)两个子区间内的元素次序则无任何保证,这一点也是它与partial_sort很大的不同处。以此观之，nth_element比较近似partition而非sort或partial_sort。

例如，假设有序列{22,30, 30, 17, 33, 40, 17, 23, 22, 12, 20}, 以下操作：

nth_element(iv.begin(), iv.begin()+5, iv.end());

便是将小于*(iv.begin()+5)(本例为40)的元素晋于该元素之左，其余置 于该元素之右，并且不保证维持原有的相对位置，获得的结果为{20, 12, 22, 17, 17, 22,23,30,30,33,40}。执行完毕后的5th(th上标）个位置上的元素值22,与整个序列完整排 序后{12, 17, 17, 20, 22, 22, 23, 30, 30, 33, 40}的5th(th上标）个位置上的元素值相同。

如果以上述结果{20, 12, 22, 17, 17, 22, 23, 30, 30, 33, 40}为根据，再执行以下操作：

nth_element (iv.begin() , iv .begin() +5, iv. end(), greater<int> ()) ;

那便是将大于*(iv.begin()+5)(本例为22)的元素置于该元素之左，其余 置于该元素之右，并且不保证维持原有的相对位置。获得的结果为{40, 33, 30, 30, 23, 22, 17, 17, 22, 12, 20}。

1. 由于nth_element比partial_sort的保证更少（是的，它不保证两个子序列内的任何次序），所以它当然应该比partial_sort较快。
2. nth_element有两个版本，其差异在于如何定义某个元素小于另一个元素。第一版本使用operator<进行比较，第二个版本使用仿函数comp进行比较。注意，这个算法只接受RandomAccesslterator。
3. nth_element的做法是，不断地以median-of-3 partitioning (以首、尾、中央三点中值为枢轴之分割法，见6.7.9节）将整个序列分割为更小的左(L)、右® 子序列。如果nth迭代器落于左子序列，就再对左子序列进行分割，否则就再对 右子序列进行分割。依此类推，直到分割后的子序列长度不大于3(够小了），便对最后这个待分割的子序列做Insertion Sort, 大功告成。

下图是nth_element的操作实例拆解。以下是其源代码，只列出版本一。

//版本一
template <class RandomAccessIterator> 
inline void __nth_element(RandomAccessIterator first,RandomAccessIterator nth, RandomAccessIterator last, T*) {
while (last-first > 3) { //长度超过3
//采用median-of-3 partitioning。参数：(first, last, pivot)
//返回一个迭代器，指向分割后的右段第一个元素
RandomAccessIterator cut= __unguarded_partition(first,last,T(__median(*first,*(first + (last -first) /2) , *(last-1)))) ;
if(cut<=nth)//如果右段起点＜＝指定位置(nth落于右段）
first = cut;//如果右段起点＜＝指定位置(nth落于右段）
else//如果右段起点＜＝指定位置(nth落于右段）
last = cut;//如果右段起点＜＝指定位置(nth落于右段）
}
__insertion_sort(first,last);
}

7.13 merge sort

1. 虽然SGI STL所采用的排序法是lntroSort(一种比Quick Sort考虑更周详的 算法，见6.7.9节），不过，另一个很有名的排序算法Merge Sort, 很轻易就可以利用STL算法inplace_rnerge(6.7.11节）实现出来。
2. Merge Sort的概念是这样的：既然我们知道，将两个有序(sorted)区间归并成一个有序区间，效果不错，那么我们可以利用“分而治之"(devide and conquer) " 的概念，以各个击破的方式来对一个区间进行排序。
3. 首先，将区间对半分割，左右两段各自排序，再利用inplace_merge重新组合为一个完整的有序序列。对半分 割的操作可以递归进行，直到每一小段的长度为0或1(那么该小段也就自动完成了排序）。

下面是一份实现代码：

template <class BidirectionalIter> 
void mergesort(BidirectionalIter first, BidirectionalIter last) { 
typename iterator_traits<BidirectionalIter>::difference_type n = distance(first, last);
if (n == 0 || n == 1)
return; 
else { 
BidirectionalIter mid= first+n / 2; 
mergsort(first, mid); 
mergesort(mid, last); 
inplace_merge(first, mid, last);
}
}

Merge Sort的复杂度为O(N logN)。虽然这和Quick Sort是一样的，但因为 Merge Sort需借用额外的内存，而且在内存之间移动（复制）数据也会耗费不少时 间，所以Merge Sort的效率比不上Quick Sort。实现简单、概念简单，是Merge Sort 的两大优点。