我们知道训练模型时经常会有一些误差,我们要想弥补这些误差,首先要搞清楚这些误差是怎么产生的。
误差的分解
假设我们要预测的模型为 y=f(x),但是通常数据都会有一些噪音,我们的数据集为y=f(x)+noise,通常我们会假设数据服从正态分布,也就是噪音会均分分布在曲线两侧,所以噪音和为0。
假设有测试数据 x,yD为其在数据集中的label(有噪声的label),y为其真实的label(无噪声的label),f(x;D)为训练集上得到的模型对x的预测值,
那么模型的误差为 E[(f(x;D)-yD)2],即预测值与数据集中的label的差的平方,即均方差,
此外,我们知道模型在不同训练集上学到的模型很可能不同,即使数据属于同一个分布,也就是说不同的数据集得到的模型对x预测会得到不同的f(x;D),
那么在不同训练集上得到的模型的预测期望为 f(x)=E(f(x;D)),E代表期望
在不同训练集上得到的模型的预测方差为 var=E[(f(x;D)-f(x))2],也就是预测值的离散程度,
最终在不同训练集上得到的模型的预测偏差为 bias=f(x)-y,也就是预测值与真实值之间的差叫偏差,
首先对误差进行分解
记 E[(yD-y)] 为噪声,通常我们默认会忽略噪声,认为数据质量可以,或者说数据服从正态分布,噪声均值为0,所以 E[(yD-y)]=0
我们发现误差是由方差、偏差和噪音三部分组成的。
好了,重新来认识下这三部分
方差是不同数据集上学到的模型对同一样本进行预测的值的方差,其反映了数据对模型的扰动影响;
偏差是不同数据集上学到的模型对同一样本进行预测的均值和真实值之间的差,其反映了模型的“准度”,即模型的拟合能力,
噪音反映了数据的质量,它决定了模型所能达到的极限,也就是模型期望泛化误差的下界
所以模型的好坏是由 算法本身的能力、数据的充分性和数据的质量来决定的。
通常我们认为数据不存在噪声,所以要想提高模型的准度,就需要较小的方差,较小的偏差。
偏差与方差的窘境
偏差是模型的拟合能力,我们知道,模型在不同的训练阶段有不同的拟合能力,如欠拟合,过拟合等,
当模型欠拟合时,模型从数据身上只学到很少的东西甚至什么也没学到,那么它受数据的影响就很小,方差就很小,而欠拟合时偏差很大,
当模型过拟合时,模型从数据身上学到了很多东西,包括一些特殊样本,那么它受数据的影响就很大,方差就很大,而过拟合时偏差很小,
所以偏差和方差是冲突的。
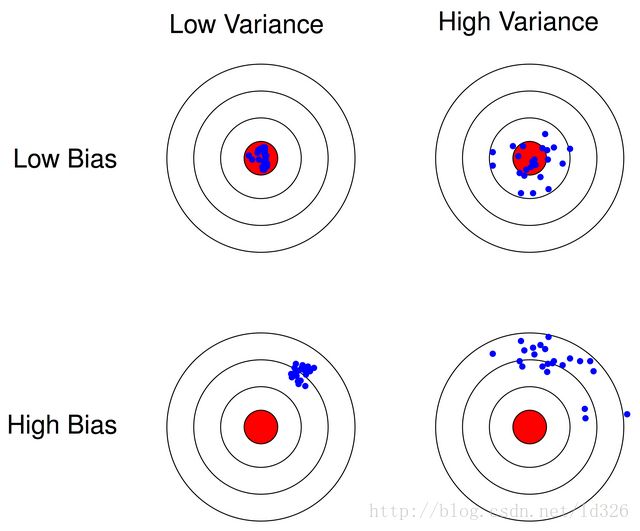
用一张图来表示两者之间的关系
其中红色代表真实值,蓝色代表预测值
左上角:低偏差低方差,蓝色离红色很近,低偏差,蓝色很集中,低方差
右上角:低偏差高方差,蓝色离红色很近,低偏差,蓝色很分散,高方差
左下角:高偏差低方差,同理
右下角:高偏差高方差
为了降低模型的误差,我们需要对两者进行权衡
可以看到偏差和方差随着训练程度的加深,会在某个地方相交,这个地方就是两者权衡后的最佳方案,此时泛化误差最小。
总结
1. 模型越简单,稳定性越好,在测试集上的表现稳定,但不能代表表现好,
2. 模型越复杂,稳定性越差,在训练集上表现很好,但在测试集上基本表现糟糕
3. 这种现象是因为我们用有限的数据来估计无限的总体,两者之间总会有一些差异。
当我们更相信这些训练样本,而忽视对模型的先验知识,就会提高模型的训练样本上的准确度,减少偏差;这样得到的模型泛化能力差,过拟合,降低在真实数据上的表现
如果我们更相信先验知识,在学习模型的过程中对模型增加多种限制,就可以降低模型的方差,提高模型的稳定性;但是会增加偏差
参数调节
偏差和方差可以用来调参,控制模型的训练程度。
高偏差低方差-欠拟合
增加模型复杂度
增加特征
降低正则化
增加学习次数
低偏差高方差-过拟合
降低模型复杂度
增加训练实例
增加正则化
减少特征
参考资料:
https://blog.csdn.net/ld326/article/details/79532847