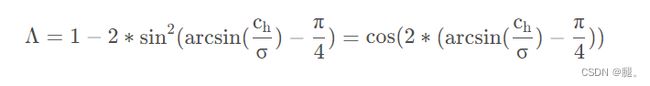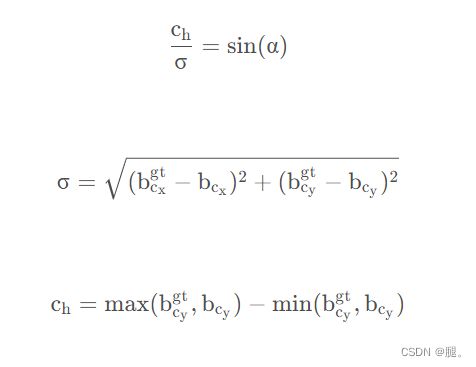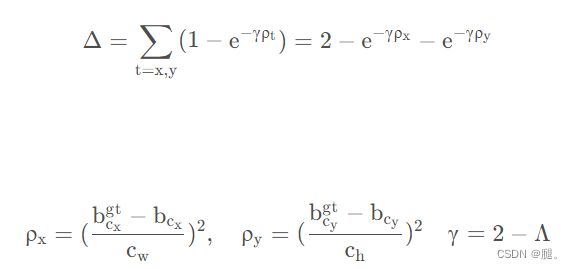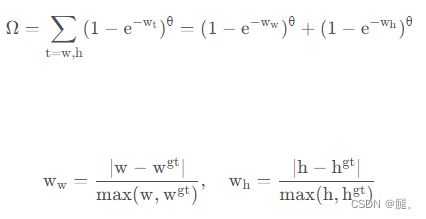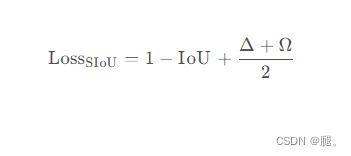新的损失函数SIoU：结合图片和详细代码分块深入理解原理

一、前言

        原文地址https://arxiv.org/abs/2205.12740

        SIoU进一步考虑了真实框和预测框之间的向量角度，重新定义相关损失函数，具体包含四个部分：角度损失(Angle cost)、距离损失(Distance cost)、形状损失(Shape cost)、IoU损失（IoU cost）。

二、分块分析

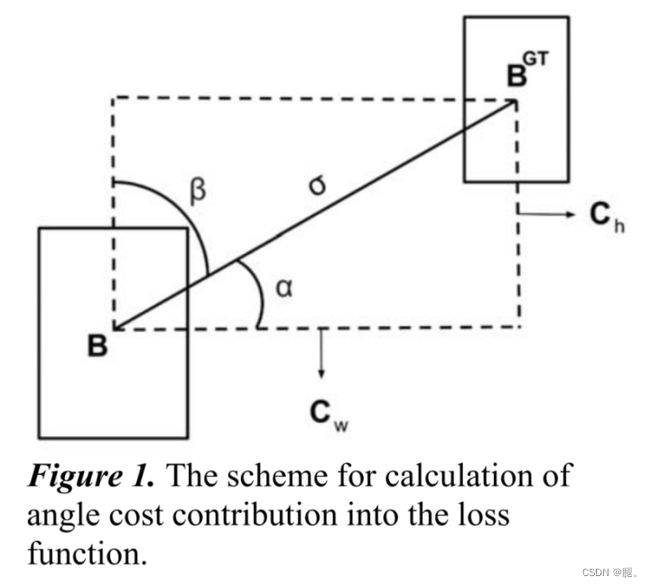
        1、角度损失(Angle cost)

        sin()看公示可以知道，就是直角三角形中的对边比斜边，在训练过程中若α大于45°则取β，否则取α。

        为真实框和预测框中心点的距离。

       为真实框和预测框中心点的高度差，代码中直接使用勾股定理求得。

          ,  为真实框中心坐标，，为预测框中心坐标

 

import torch
import math
# [[x, y, w, h]]
# [[x, y, w, h]] : 中心点坐标和宽高
pred = torch.tensor([[1, 2, 3, 4]])
gt = torch.tensor([[5, 6, 7, 8]])
iou = 0.5  # 这里设置iou为0.5
def siou1():
    # --------------------角度损失(Angle cost)------------------------------
    gt_p_center_D_value_w = torch.abs((gt[:, 0] - pred[:, 0]))  # 真实框和预测框中心点的宽度差
    gt_p_center_D_value_h = torch.abs((gt[:, 1] - pred[:, 1]))  # 真实框和预测框中心点的高度差
    sigma = torch.pow(gt_p_center_D_value_w ** 2 + gt_p_center_D_value_h ** 2, 0.5)  # 真实框和预测框中心点的距离
    sin_alpha = torch.abs(gt_p_center_D_value_w) / sigma  # 真实框和预测框中心点的夹角α
    sin_beta = torch.abs(gt_p_center_D_value_h) / sigma  # 真实框和预测框中心点的夹角β
    threshold = torch.pow(torch.tensor(2.), 0.5) / 2  # 夹角阈值 0.7071068 = sin45° = 二分之根二
    # torch.where(condition，a，b)其中
    # 输入参数condition：条件限制，如果满足条件，则选择a，否则选择b作为输出。
    sin_alpha = torch.where(sin_alpha > threshold, sin_beta, sin_alpha)  # α大于45°则考虑优化β，否则优化α
    angle_cost = torch.cos(2 * (torch.arcsin(sin_alpha) - math.pi / 4))

        2、距离损失(Distance cost)

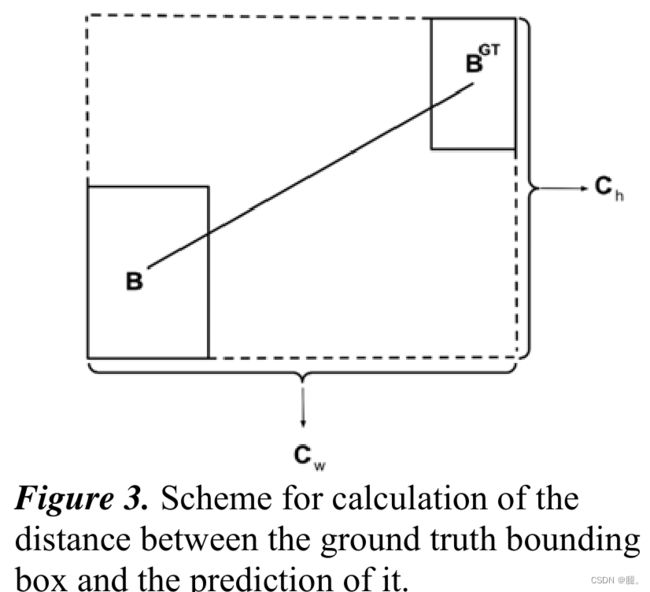
                    与真实框和预测框的最小外接矩形有关

                      ，为真实框和预测框最小外接矩形的宽和高

 

 # -----------------距离损失(Distance cost)-----------------------------
    # min_enclosing_rec_tl：最小外接矩形左上坐标
    # min_enclosing_rec_br：最小外接矩形右下坐标
    min_enclosing_rec_tl = torch.min(
                (pred[:, :2] - pred[:, 2:] / 2), (gt[:, :2] - gt[:, 2:] / 2))
    min_enclosing_rec_br = torch.max(
                (pred[:, :2] + pred[:, 2:] / 2), (gt[:, :2] + gt[:, 2:] / 2))

    # 最小外接矩形的宽高
    min_enclosing_rec_br_w = (min_enclosing_rec_br - min_enclosing_rec_tl)[:, 0]
    min_enclosing_rec_br_h = (min_enclosing_rec_br - min_enclosing_rec_tl)[:, 1]

    # 真实框和预测框中心点的宽度(高度)差 / 以最小外接矩形的宽（高） 的平方
    rho_x = (gt_p_center_D_value_w / min_enclosing_rec_br_w) ** 2
    rho_y = (gt_p_center_D_value_h / min_enclosing_rec_br_h) ** 2

    gamma = 2 - angle_cost
    # 距离损失
    distance_cost = 2 - torch.exp(-gamma * rho_x) - torch.exp(-gamma * rho_y)

        3、形状损失(Shape cost)

                w,h,,分别为预测框和真实框的宽和高，控制对形状损失的关注程度，为了避免过于关注形状损失而降低对预测框的移动，作者使用遗传算法计算出接近4，因此作者定于参数范围为[2, 6]

# ----------------形状损失(Shape cost)----------------------
    w_pred = pred[:, 2]  # 预测框的宽
    w_gt = gt[:, 2]  # 真实框的宽
    h_pred = pred[:, -1]  # 预测框的高
    h_gt = gt[:, -1]  # 真实框的高
    # 预测框的宽 - 真实框的宽的绝对值 / 预测框的宽和真实框的宽中的最大值
    omiga_w = torch.abs(w_pred - w_gt) / torch.max(w_pred, w_gt)
    omiga_h = torch.abs(h_pred - h_gt) / torch.max(h_pred, h_gt)

    # 作者使用遗传算法计算出θ接近4，因此作者定于θ参数范围为[2, 6]
    theta = 4
    # 形状损失
    shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), theta) + torch.pow(1 - torch.exp(-1 * omiga_h), theta)

4、IoU损失(IoU cost)

        可以看看之前的学习随笔

通过PYTHON画图来理解IOU的计算（学习随笔）

5、最终SIoU损失函数定义如下：

三、完整代码（可直接运行）

import torch
import math
# [[x, y, w, h]]
# [[x, y, w, h]] : 中心点坐标和宽高
pred = torch.tensor([[1, 2, 3, 4]])
gt = torch.tensor([[5, 6, 7, 8]])
iou = 0.5  # 这里设置iou为0.5
def siou1():
    # --------------------角度损失(Angle cost)------------------------------
    gt_p_center_D_value_w = torch.abs((gt[:, 0] - pred[:, 0]))  # 真实框和预测框中心点的宽度差
    gt_p_center_D_value_h = torch.abs((gt[:, 1] - pred[:, 1]))  # 真实框和预测框中心点的高度差
    sigma = torch.pow(gt_p_center_D_value_w ** 2 + gt_p_center_D_value_h ** 2, 0.5)  # 真实框和预测框中心点的距离
    sin_alpha = torch.abs(gt_p_center_D_value_w) / sigma  # 真实框和预测框中心点的夹角β
    sin_beta = torch.abs(gt_p_center_D_value_h) / sigma  # 真实框和预测框中心点的夹角α
    threshold = torch.pow(torch.tensor(2.), 0.5) / 2  # 夹角阈值 0.7071068 = sin45° = 二分之根二

    # torch.where(condition，a，b)其中
    # 输入参数condition：条件限制，如果满足条件，则选择a，否则选择b作为输出。
    sin_alpha = torch.where(sin_alpha > threshold, sin_beta, sin_alpha)  # α大于45°则考虑优化β，否则优化α

    # angle_cost = torch.cos(torch.arcsin(sin_alpha) * 2 - math.pi / 2)  # 角度损失
    angle_cost = torch.cos(2 * (torch.arcsin(sin_alpha) - math.pi / 4))

    # -----------------距离损失(Distance cost)-----------------------------
    # min_enclosing_rec_tl：最小外接矩形左上坐标
    # min_enclosing_rec_br：最小外接矩形右下坐标
    min_enclosing_rec_tl = torch.min(
                (pred[:, :2] - pred[:, 2:] / 2), (gt[:, :2] - gt[:, 2:] / 2))
    min_enclosing_rec_br = torch.max(
                (pred[:, :2] + pred[:, 2:] / 2), (gt[:, :2] + gt[:, 2:] / 2))

    # 最小外接矩形的宽高
    min_enclosing_rec_br_w = (min_enclosing_rec_br - min_enclosing_rec_tl)[:, 0]
    min_enclosing_rec_br_h = (min_enclosing_rec_br - min_enclosing_rec_tl)[:, 1]

    # 真实框和预测框中心点的宽度(高度)差 / 以最小外接矩形的宽（高） 的平方
    rho_x = (gt_p_center_D_value_w / min_enclosing_rec_br_w) ** 2
    rho_y = (gt_p_center_D_value_h / min_enclosing_rec_br_h) ** 2

    gamma = 2 - angle_cost
    # 距离损失
    distance_cost = 2 - torch.exp(-gamma * rho_x) - torch.exp(-gamma * rho_y)

    # ----------------形状损失(Shape cost)----------------------
    w_pred = pred[:, 2]  # 预测框的宽
    w_gt = gt[:, 2]  # 真实框的宽
    h_pred = pred[:, -1]  # 预测框的高
    h_gt = gt[:, -1]  # 真实框的高
    # 预测框的宽 - 真实框的宽的绝对值 / 预测框的宽和真实框的宽中的最大值
    omiga_w = torch.abs(w_pred - w_gt) / torch.max(w_pred, w_gt)
    omiga_h = torch.abs(h_pred - h_gt) / torch.max(h_pred, h_gt)

    # 作者使用遗传算法计算出θ接近4，因此作者定于θ参数范围为[2, 6]
    theta = 4
    # 形状损失
    shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), theta) + torch.pow(1 - torch.exp(-1 * omiga_h), theta)

    #------------------loss_siou----------------------------
    siou = 1.0 - iou + 0.5 * (distance_cost + shape_cost)

    print(siou)

siou1()