【C语言】递归详解汉诺塔问题

前言

汉诺塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。当把64片圆盘从第一根石柱移动到第三根石柱时，这个世界就会毁灭。

而婆罗门移动圆盘需要用多长时间呢？通过平常的方法是很难计算的。

今天我们就利用递归的思想来计算一下汉诺塔的移动次数和汉诺塔的移动步骤！

汉诺塔移动图解

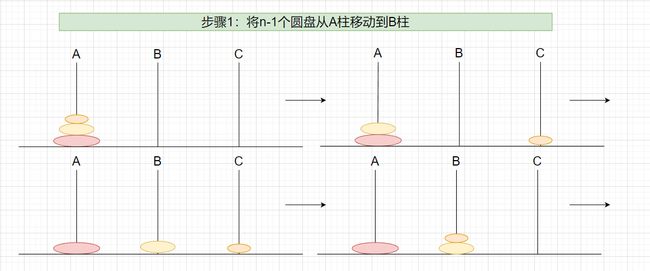
汉诺塔移动的规律为一次只能移动一个圆盘，并且小盘要在大盘的上方，假设在A柱有n个圆盘，我们先要把n-1个圆盘从A柱移动到B柱，再把第n个圆盘移动到C柱，最后把n-1个圆盘移动到C柱。

以三阶汉诺塔为例：

汉诺塔移动次数

利用穷举的办法，对于汉诺塔的移动次数进行计算：

阶数	次数	规律
1	1	2^1-1
2	3	2^2-1
3	7	2^3-1
4	15	2^4-1
…	…	2^n-1

对于n阶汉诺塔的移动次数：

• 步骤1所含步数就是n-1个圆盘移动所需的次数，我们可以将其步数看做f(n-1)。
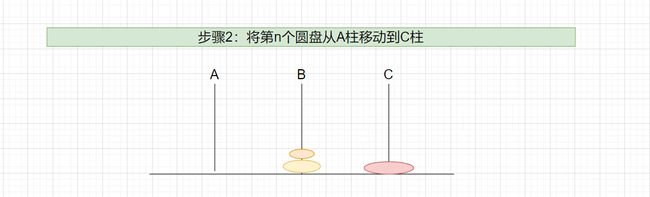
• 步骤2所含步数为1。
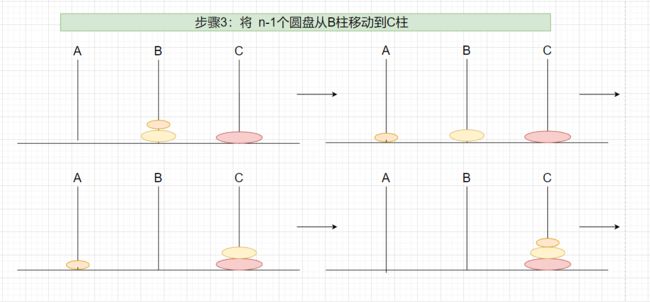
• 步骤3所含步数与步骤1相似，我们也将其步数看做f(n-1)。

再观察表格中汉诺塔的移动次数，对于一阶汉诺塔移动次数就为1，对于其他的阶数则为前一阶汉诺塔移动次数 + 1 + 前一阶汉诺塔移动次数。

不难得出递推表达式：f(n-1) + 1 + f(n-1) = 2 * f(n - 1) + 1

移动步骤符合递归思想，代码展示：

#include
int hanoi_step(int n)
{
	if(n<=1)
		return 1;
	else
		return 2*hanoi_step(n-1)+1;
}
int main()
{
	int n = 0;
	scanf("%d",&n);
	int ret = hanoi_step(n);
	printf("%d\n",ret);
	return 0;
}

运行结果：

汉诺塔的打印

这里的打印指的是打印汉诺塔移动的步骤。

我们可以先尝试写出1-4阶汉诺塔的移动步骤：

阶数	步骤
1	A->C
2	A->B，A->C，B->C
3	A->C，A->B，C->B，A->C，B->A，B->C，A->C
4	A->B，A->C，B->C，A->B，C->A，C->B，A->B，A->C，B->C，B->A，C->A，B->C，A->B，A->C，B->C

我们观察移动步骤，发现只有一个圆盘时移动步骤为A->C；两个圆盘时，为A->B，A->C，B->C。

那么对于n阶汉诺塔呢，我们对其进行推演：

• 把n-1个圆盘从A移动到B
• 把第n个圆盘从A移动到C
• 把n-1个圆盘从B移动到C

那n-1个圆盘如何从A移动到B呢？

• 把n-2个圆盘从A移动到C
• 把第n-1个圆盘从A移动到B
• 把n-2个圆盘从C移动到B

同样的，对于把n-1个圆盘从B移动到C，也可以推测出来：

• 把n-2个圆盘从B移动到A
• 把第n-1个圆盘从B移动到C
• 把n-2个圆盘从A移动到C

通过这些推演我们发现，汉诺塔的移动可以通过递归展开，那么以上推演步骤，我们可以将其作为递归的步骤。

思路：定义A,B,C三个字符，表示A,B,C三柱，定义n为阶数，那么n-1也就是移动步骤中，需要移动的圆盘数。
对于一阶汉诺塔，直接移动即可，对于其他的阶数，则需要通过递归展开，为n阶汉诺塔的移动步骤。

#include
void hanoi_move(int n,char A,char B,char C)
{
	if(1==n)
	{
		printf("%c->%c\n",A,C);
	}
	else
	{
		hanoi_move(n-1,A,C,B);//将n-1个圆盘从A移动到B
		printf("%c->%c\n",A,C);//将第n个圆盘从A柱移动到C柱
		hanoi_move(n-1,B,A,C);//将n-1个圆盘从B柱移动到C柱
	}
}
int main()
{
	int n = 0;
	scanf("%d",&n);
	hanoi_move(n,'A','B','C');
	return 0;
}

只通过代码可能不太直观，我们以三阶汉诺塔为样例，观察递归是如何展开的：

运行结果：

结语

了解了汉诺塔的移动步数和过程，我们也可以对64片黄金圆盘移动完需要的时间做一个估算，将每次移动看作一秒，那么时间为：2 ^ 64 - 1 = 18,446,744,073,709,551,615秒，换算成年数，约为5800亿年。

按照这个进度，到时候世界毁灭也是有可能的，只是可怜了“悲惨的婆罗门”需要移动这些圆盘(doge)。

以上就是C语言递归求解汉诺塔的全部内容，如果觉得anduin写的还不错的话，还请一键三连！

我是anduin，一名C语言初学者，我们下期见！