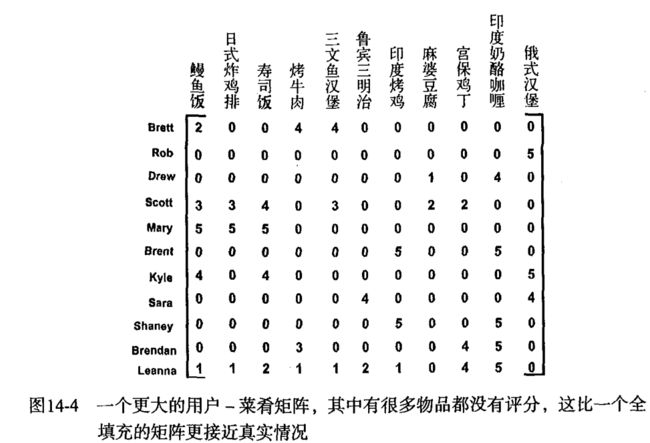
《机器学习实战》学习笔记（十四）

第14章 利用SVD简化数据

引言

奇异值分解（Singular Value Decomposition SVD )是提取信息的强大工具。

奇异值分解优缺点：

• 优 点 ：简化数据，去除嗓声，提高算法的结果。
• 缺 点 ：数据的转换可能难以理解。
• 适用数据类型：数值型数据

14.1 SVD的应用

利用SVD实现，我们能够用小得多的数据集来表示原始数据集。这样做，实际上是去除了噪声和冗余信息。当我们试图节省空间时，去除信息就是很崇高的目标了，但是在这里我们则是从数据中抽取信息。基于这个视角，我们就可以把SVD看成是从噪声数据中抽取相关特征。

最早的SVD应用之一就是信息检索。我们称利用SVD的方法为隐性语义索引（Latent Semantic Indexing, LSI) 或隐性语义分析（Latent Semantic Analysis, LSA)。

SVD的另一个应用就是推荐系统。简单版本的推荐系统能够计算项或者人之间的相似度。更先进的方法则先利用SVD从数据中构建一个主题空间，然后再在该空间下计算其相似度。

SVD是矩阵分解的一种类型，而矩阵分解是将数据矩阵分解为多个独立部分的过程。

14.2 矩阵分解

在很多情况下，数据中的一小段携带了数据集中的大部分信息，其他信息则要么是噪声，要么就是毫不相关的信息。在线性代数中还有很多矩阵分解技术。矩阵分解可以将原始矩阵表示成新的易于处理的形式，这种新形式是两个或多个矩阵的乘积。我们可以将这种分解过程想象成代数中的因子分解。

SVD将原始的数据集矩阵分解成三个矩阵U、$\sum$和$V^T$。如果原始矩阵Data是m行n列，那么U、$\sum$和$V^T$就分别是m行m列、m行n列和n行n列该过程可以表示为：
$$Dat{a}_{m\ast n}=U_{m\ast m}\sum _{m\ast n}{V}_{n\ast n}^T$$

上述分解中会构建出一个对角矩阵$\sum$。另一个惯例就是，$\sum$的对角元素是从大到小排列的。这些对角元素称为奇异值（singular Value），它们对应了原始数据集矩阵Data的奇异值。在PCA中，我们得到的是矩阵的特征值，它们告诉我们数据集中的重要特征。$\sum$中的奇异值也是如此。奇异值和特征值是有关系的。这里的奇异值就是矩阵$Data\ast Dat{a}^T$特征值的平方根。

矩阵$\sum$只有从大到小排列的对角元素。在科学和工程中，一直存在这样一个普遍事实：在某个奇异值的数目（r个）之后，其他的奇异值都置为0。这就意味着数据集中仅有r个重要特征，而其余特征则都是噪声或冗余特征。

14.3 利用python实现SVD

from numpy import *
from numpy import linalg as la

def loadExData():
   return[[1,1,1,0,0],
       [2,2,2,0,0],
       [1,1,1,0,0],
       [5,5,5,0,0],
       [1,1,0,2,2],
       [0,0,0,3,3],
       [0,0,0,1,1]]
       
Data = loadExData()
u,Sigma,VT = linalg.svd(Data)

print(Sigma)

输出结果为

[9.72140007e+00 5.29397912e+00 6.84226362e-01 4.11502614e-16
 1.36030206e-16]

输出值为sigma的值。其中前3个数值比其他的值大了很多，于是，我们就可以将最后两个值去掉了。

原始数据集就可以用如下结果来近似：
$$Dat{a}_{m\ast 3}\approx U_{3\ast 3}\sum _{m\ast n}{V}_{3\ast n}^T$$

上述过程近似示意图：

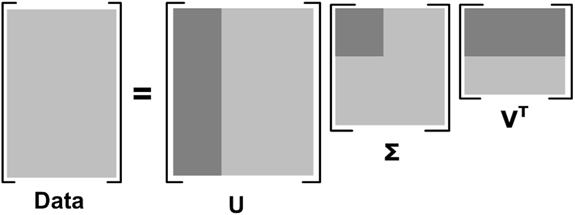
矩阵Data被分解。浅灰色区域是原始数据，深灰色区域是矩阵近似计算仅需要的数据

重构原始矩阵。首先构建一个3X3的矩阵sig3:

Sig3 = mat([[Sigma[0],0, 0],[0, Sigma[1], 0], [0,0, Sigma[2]]])
reData =  u[:,:3] * Sig3 * VT[:3,:]
print(reData)

之后借助公式，对数据进行重建。
输出结果如下：

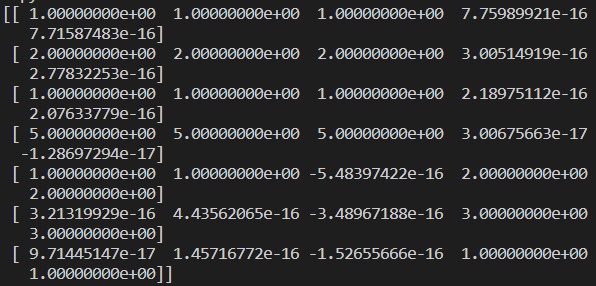
上图中输出结果看似与原始数据不同，但是仔细观察便会发现，原始矩阵中为0的位置，在这个新构建的矩阵中对应的值都是特别小的值，应当可以忽略。对比下来与原始值是一致的。

如何确定要保留的奇异值的数目

确定要保留的奇异值的数目有很多启发式的策略 ，其中一个典型的做法就是保留矩阵中90%的能量信息。为了计算总能量信息，我们将所有的奇异值求其平方和。于是可以将奇异值的平方和累加到总值的90%为止。

另一个启发式策略就是，当矩阵上有上万的奇异值时，那么就保留前面的2000或3000个 。尽管后一种方法不太优雅，但是在实际中更容易实施。之所以说它不够优雅，就是因为在任何数据集上都不能保证前3000个奇异值就能够包含90 % 的能量信息。但在通常情况下，使用者往往都对数据有足够的了解，从而就能够做出类似的假设了。

14.4 基于协同过滤的推荐引擎

协同过滤 ( collaborative filtering )是通过将用户和其他用户的数据进行对比来实现推荐的。

14.4.1相似度计算

不利用专家所给出的重要属性来描述物品从而计算它们之间的相似度,而是利用用户对它们的意见来计算相似度。这就是协同过滤中所使用的方法。并不关心物品的描述属性，而是严格地按照许多用户的观点来计算相似度。

使用欧氏距离来计算手撕猪肉和烤牛肉之间的相似度：
$$\sqrt{(4-4{)}^2+(3-3{)}^2+(1-2{)}^2}=1$$

手撕猪肉和鳗鱼饭的欧氏距离为:
$$\sqrt{(2-4{)}^2+(5-3{)}^2+(2-2{)}^2}=2.83$$

在该数据中，由于手撕猪肉和烤牛肉的距离小于手撕猪肉和鳗鱼饭的距离，因此手撕猪肉与烤牛肉比与鳗鱼饭更为相似。

我们希望，相似度值在0到1之间变化，并且物品对越相似，它们的相似度值也就越大。我们可以用“相似度=1/(1+距离)”这样的算式来计算相似度。当距离为0时，相似度为1.0。如果距离真的非常大时，相似度也就趋近于0。

第二种计算距离的方法是皮尔逊相关系数（Pearson correlation )。它度量的是两个向量之间的相似度。该方法相对于欧氏距离的一个优势在于，它对用户评级的量级并不敏感。皮尔逊相关系数的取值范围从-1到+1，我们通过0.5 + 0 . 5 *corrcoef() 这个函数计算，并且把其取值范围归一化到0到1之间。

另一个常用的距离计算方法就是余弦相似度（cosine similarity)，其计算的是两个向量夹角的余弦值。如果夹角为90度 ，则相似度为0 ; 如果两个向量的方向相同，则相似度为1.0。余弦相似度的取值范围也在-1到+1之间，因此我们也将它归一化到0到1之间。

计算余弦相似度值，我们采用的两个向量A和B夹角的余弦相似度的定义如下：
$$cos\theta =\frac{A\cdot B}{||A||||B||}$$
$||A||、||B||$表示向量A、B的2范数，你可以定义向量的任一范数，但是如果不指定范数阶数，则都假设为2范数。向量[4,2,2]的2范数为：
$$\sqrt{4^2+2^2+2^2}$$

相似度计算实现程序如下：

def ecludSim(inA,inB):
    """ 欧式距离相似度 """
    # norm函数是求模长的,实际就是将差值平方和开方
    return 1.0/(1.0 + la.norm(inA - inB))


def pearsSim(inA,inB):
    """ 皮尔逊相关系数相似度 """
    if len(inA) < 3 : return 1.0

    return 0.5+0.5*corrcoef(inA, inB, rowvar = 0)[0][1]

def cosSim(inA,inB):
    """ 余弦相似度 """
    # 公式中的A.B
    num = float(inA.T*inB)
    # 公式中的||A|| ||B||
    denom = la.norm(inA)*la.norm(inB)
    return 0.5+0.5*(num/denom)


def main():

    myMat = mat(loadExData())

    eclDist = ecludSim(myMat[:,0], myMat[:,4])
	samEclDist = ecludSim(myMat[:,0], myMat[:,0])
	cosDist = cosSim(myMat[:,0], myMat[:,4])
	samCosDist = cosSim(myMat[:,0], myMat[:,0])
	pearDist = pearsSim(myMat[:,0], myMat[:,4])
	samPearDist = pearsSim(myMat[:,0], myMat[:,0])
	print('eclDist :',eclDist)
	print('sameEclDist :',samEclDist)
	print('cosDist :',cosDist)
	print('samCosDist :',samCosDist)
	print('pearDist :',pearDist)
	print('samPearDist :',samPearDist)

    return

输出结果如下：

输出结果可以看到，不同的算法对于同样的数据得到的相似度不同。但是对于同样的数据得到的结果是接近于1的。

计算了两个餐馆菜肴之间的距离，这称为基于物品（item-based)的相似度。另一种计算用户距离的方法则称为基于用户（user -based）的相似度。回到图14-3，行与行之间比较的是基于用户的相似度，列与列之间比较的则是基于物品的相似度。

通常用于推荐引擎评价的指标是称为最小均方根误差（Root Mean Squared Error, RMSE)的指标，它首先计算均方误差的平均值然后取其平方根。

14.5 示例：餐馆菜肴推荐引擎

推荐系统的工作过程是：给定一个用户，系统会为此用户返回N个最好的推荐菜。为了实现这一点，则需要我们做到：

1. 寻找用户没有评级的菜肴，即在用户- 物品矩阵中的0值 ；
2. 在用户没有评级的所有物品中，对每个物品预计一个可能的评级分数。这就是说，我们认为用户可能会对物品的打分(这就是相似度计算的初衷）；
3. 对这些物品的评分从高到低进行排序，返回前N物品 。

基于物品相似度的推荐引擎程序实现

def standEst(dataMat, user, simMeas , item ):
    '''
    函数功能：通过物品评分的相似度来计算用户未评分过的物品
    参数说明：
            dataMat__用户-物品评分矩阵
            user__第user个用户(从0开始算)
            simMeas__计算相似度的函数，默认是cosSim()
            item__该用户未进行评分的物品
    函数返回：
            用户未进行评分的物品item的分数
    '''
    #item是该user还未评分的物品，j则是该user已评分的物品。通过计算
    # 与其他用户评分的相似度，得出该user还未评分的相似。
    n = shape(dataMat)[1]
    #物品数量
    simTotal = 0.0
    #相似度总和
    ratSimTotal = 0.0
    #评分总和
    for j in range(n):
        print(item,j)
        #user对第j个物品的评分
        userRating = dataMat[user,j]
        #为0则跳出本次循环，为零说明该物品也没有评分
        if userRating == 0: 
            continue
        #overlap是两个物品当中已经被评分的用户
        # 找出已评分物品那一列、和未评分物品这一列中，都被评过分的行号
        overLap = nonzero(logical_and(dataMat[:,item].A>0, dataMat[:,j].A>0))[0]
        #如果没有对user未评分的物品评过分的用户，那么similarity是0
        if len(overLap) == 0:
            similarity = 0
        else:
            #基于这些重合的物品计算用户与user之间的相似度
            similarity = simMeas(dataMat[overLap,item], dataMat[overLap,j])
        print('the %d and %d similarity is: %f' % (item, j, similarity))
        #计算总相似度
        simTotal += similarity
        #相似度乘上userRating
        ratSimTotal += similarity * userRating

    if simTotal == 0:
        return 0
    else:
        print('uR',ratSimTotal/simTotal)
        #除以总相似度
        return ratSimTotal/simTotal

def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst):
    '''
    函数功能：通过物品评分的相似度来计算用户未评分过的物品，并返回分数最高的前N个物品
    参数说明：
            dataMat__用户-物品评分矩阵
            user__第user个用户(从0开始算)
            N__分数最高的前N个物品
            simMeas__计算相似度的函数，默认是cosSim()
            estMethod__计算未评分物品相似度的函数，默认是standEst()
    函数返回：
            分数最高的前N个物品
    '''
    #  nonzero()[1]返回的是非零值所在的行数，返回的是一个元组
    # 找到用户已评分的物品
    unratedItems = nonzero(dataMat[user,:].A==0)[1] 

    if len(unratedItems) == 0:
        return 'you rated everything'  
    itemScores = []
    # 对已经评分的菜进行计算
    for item in unratedItems:
        # 预测未评分物品分数
        estimatedScore = estMethod(dataMat, user, simMeas, item)
        print(estimatedScore)
        itemScores.append((item, estimatedScore))
    return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[:N]


def main():
    myMat = mat(loadExData())
    myMat[0,1] = myMat[0,0] = myMat[1,0] = myMat[2,0] = 4
    myMat[3,3] = 2

    print (myMat)

    recom = recommend(myMat, 2)

    print ('recom is:',recom)
    return

输出结果如下：

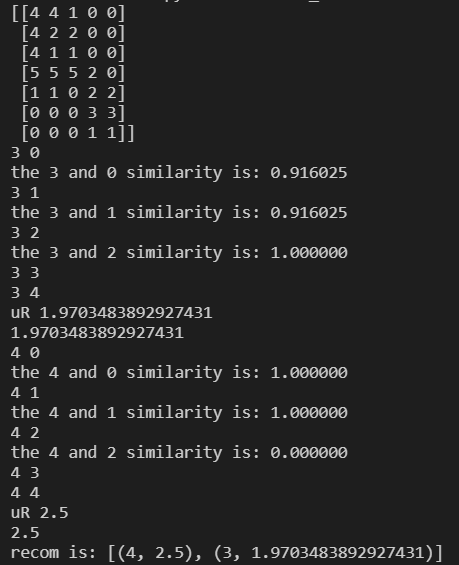
我们需要程预测第三位顾客，没有评分的物品4和物品5。最终输出结果物品5预测评分2.5，物品4预测评分1.97.

程序默认使用的相似度计算方法是余弦相似度，更换一下相似度计算方法，得到结果如下：

recom = recommend(myMat, 2 , simMeas=pearsSim)
print ('pearsSim recom is:',recom)
recom = recommend(myMat, 2 , simMeas=ecludSim)
print ('ecludSim recom is:',recom)

输出结果如下：

pearsSim recom is: [(4, 2.5), (3, 2.0)]

ecludSim recom is: [(4, 2.5), (3, 1.98665729687295)]

对比输出结果可以发现，三种相似度给出的预测结果大致相同。

14.5.2 利用SVD提高推荐的效果

计算该矩阵的SVD来了解其到底需要多少维特征。

 Data = loadExData2()
 u,Sigma,VT = linalg.svd(mat(Data))
 print (Sigma)
 

输出结果如下：

[15.77075346 11.40670395 11.03044558  4.84639758  3.09292055  2.58097379
  1.00413543  0.72817072  0.43800353  0.22082113  0.07367823]

我们取包含总能量的90%的元素。

Data = loadExData2()
    u,Sigma,VT = linalg.svd(mat(Data))

    print (Sigma)
    
    Sig2 = Sigma**2
    print("total energy",sum(Sig2))
    print("the total energy 90%:",sum(Sig2)*0.9)
    print("the first and sencond energy:",sum(Sig2[:2]))
    print("the first and sencond and third energy:",sum(Sig2[:3]))

可以看到前三个元素包含的能量达到了总能量的90%。所以我们可以将一个11维的矩阵转换成一个3维的矩阵。我们利用SVD将所有的菜肴映射到一个低维空间中去。在低维空间下，可以利用前面相同的相似度计算方法来进行推荐。

基于SVD的评分估计

def svdEst(dataMat, user, simMeas, item):
    """
    函数功能：通过物品评分的相似度来计算用户未评分过的物品，并返回分数最高的前N个物品
    参数说明：
        dataMat__用户-物品评分表
        user__第user个用户(从0开始算)
        simMeas__计算相似度的函数，默认是cosSim()
        item__ 未评分物品的列数
    函数返回：
        分数最高的前N个物品
     """

    n = shape(dataMat)[1]
    simTotal = 0.0; ratSimTotal = 0.0
    #注意这里调用了la.svd()求出了dataMat的奇异值
    U,Sigma,VT = la.svd(dataMat)
    #将Sigma转换为3*3矩阵，为降维dataMat做准备
    #arrange Sig4 into a diagonal matrix
    # eyes()输出对角矩阵
    Sig4 = mat(eye(3)*Sigma[:3]) 
    #利用奇异值和U将dataMat转换为11*3矩阵
    #create transformed items  
    xformedItems = dataMat.T * U[:,:3] * Sig4.I 

    for j in range(n):
        userRating = dataMat[user,j]
        if userRating == 0 or j==item: continue
        #注意这里是xformedItems[item,:]，与之前不同在于两点,一个是利用降维后的xformedItems求相似度，二就是矩阵转置了，所以用[item,:]得出item的评分，注意之后调用了转置，将行向量转换为了列向量
        similarity = simMeas(xformedItems[item,:].T,\
                             xformedItems[j,:].T)
        #print('the %d and %d similarity is: %f' % (item, j, similarity))
        simTotal += similarity
        ratSimTotal += similarity * userRating
    if simTotal == 0: return 0
    else: return ratSimTotal/simTotal

def main():
    Data = loadExData2()
    recommend1 = recommend(mat(Data), 1,estMethod=svdEst)
    recommend2 = recommend(mat(Data), 1,estMethod=svdEst,simMeas= pearsSim)
    recommend3 = recommend(mat(Data), 1,estMethod=svdEst,simMeas=ecludSim)
    print("cosSim   recommend1 : ",recommend1)
    print("pearsSim recommend2 : ",recommend2)
    print("ecludSim recommend3 : ",recommend3)
    
    return

输出结果如下：

osSim   recommend1 :  [(6, 3.332949990145984), (9, 3.331544717872839), (4, 3.331447487712862)]
pearsSim recommend2 :  [(6, 3.3311997297614164), (9, 3.328590826556045), (4, 3.3284563489329737)]
ecludSim recommend3 :  [(4, 3.325192357725485), (9, 3.324980728190185), (8, 3.321276738399071)]
program running time is : 0.08200478553771973

该函数的不同之处就在于它对数据集进行了SVD分解。在SVD分解之后，我们只利用包含了90%能量值的奇异值。
不使用SVD分解得到结果如下：

cosSim   recommend1 :  [(6, 3.3333333333333335), (9, 3.3333333333333335), (0, 3.0)]
pearsSim recommend2 :  [(6, 3.3333333333333335), (9, 3.3333333333333335), (0, 3.0)]
ecludSim recommend3 :  [(6, 3.3333333333333335), (9, 3.3333333333333335), (7, 3.0000000000000004)]
program running time is : 0.29201674461364746

可以发现对于相同项得到预测结果基本相同，但是输出结果不是对于固定项的预测结果。而且运行时间SVD较不分解能有很大提升。

如何在缺乏数据时给出好的推荐。这称为冷启动（cold-start）问题。

14.6 基于SVD的图像压缩

def printMat(inMat, thresh=0.8):
    """
    函数功能：输出inMat
    参数说明：
        inMat__数据矩阵
        thresh__ 输出门限
    函数返回：
        NULL
    """
    for i in range(32):
        for k in range(32):
            if float(inMat[i,k]) > thresh:
                print('1,',end = "")
            else: print('0,',end = "")
        print('')


def imgCompress(numSV=3, thresh=0.8):
    """
    函数功能：调用imgCompress对img进行压缩
    参数说明：
        numSV__SV保留位数
        thresh__ 输出门限
    函数返回：
        NULL
"""
    myl = []
    for line in open('./Ch14/0_5.txt').readlines():
        newRow = []
        for i in range(32):
            newRow.append(int(line[i]))
        myl.append(newRow)
    myMat = mat(myl)
    print("****original matrix******")
    printMat(myMat, thresh)
    # SVD分解
    U,Sigma,VT = la.svd(myMat)
    SigRecon = mat(zeros((numSV, numSV)))
    for k in range(numSV):#construct diagonal matrix from vector
        SigRecon[k,k] = Sigma[k]
    #重构img
    reconMat = U[:,:numSV]*SigRecon*VT[:numSV,:]
    print("****reconstructed matrix using %d singular values******" % numSV)
    printMat(reconMat, thresh)

def main():
    imgCompress()
    return 

输出结果如下：


上图为原始数据，下图为SVD分解后重建图片。可以看到结果基本一样。
只需要两个奇异值就能相当精确地对图像实现重构。那么 ，我们到底需要多少个0-1的数字来重构图像呢？U和$V^T$都是32X2的矩阵，有两个奇异值 。因此总数字数目是64+64+2=130。和原数目1024相比，我们获得了几乎10倍的压缩比。

14.7 本章小结

SVD是一种强大的降维工具，我们可以利用SVD来逼近矩阵并从中提取重要特征。通过保留矩阵80 % ~ 90 % 的能量，就可以得到重要的特征并去掉噪声。

协同过滤则是一种基于用户喜好或行为数据的推荐的实现方法。协同过滤的核心是相似度计算方法；

本章核心SVD，本质是从数学层面讲将数据转换后进行分解。之后去掉细枝末节的数据，最后在通过数学方法将数据还原。