机器学习初步

Date: 2018-11-1 03:09
Categories: 机器学习

都是https://www.coursera.org/learn/machine-learning的笔记。

基本学习分类

监督学习（Supervised Learning）：给定一个数据集，并且已经知道正确输出看起来是什么样子，以及知道输入和输出之间的关系，也就是研究一个特定的问题。对比于无监督学习看则更加清晰。

• 回归问题：映射输入到连续函数。
• 分类问题：映射输入到离散函数。

无监督学习（Unsupervised Learning）：更像是一个开放性问题，没有正确的答案来座位反馈，所有的关系都需要在学习过程中进行归纳。

• Clustering：相同类型分组。
• Non-clustering：自行在数据中提取结构。（比如：在鸡尾酒环境中提取出清晰的人声和音乐。）

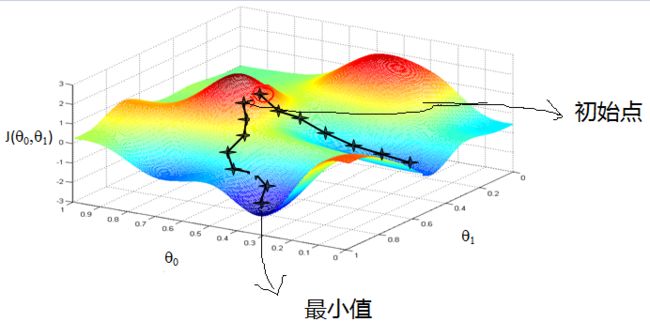
梯度下降方法

一张图解释原理：

梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

代数描述

设一个线性模型：$h_{\theta }(x_1,x_2,\dots x_n)={\theta }_0{\theta }_1{x}_1\dots {\theta }_n{x}_n$.

cost function为：
$$J({\theta }_0,{\theta }_1\dots ,{\theta }_n)=\sum _{i=0}^m(h_{\theta }(x_0,x_1,\dots x_n)–y_i{)}^2$$

在没有任何先验知识的时候我们暂且将所有$\theta$初始化为0，步长$\alpha$初始化为1.

算法过程：

• 对所有$\theta$准备梯度：$\frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1\dots ,{\theta }_n)$.
• 用步长乘以上述结果
• 确定下降距离是否都小于预先设定的$ϵ$.如果小于，精度已经足够，终止算法，当前的所有$\theta$就是结果。否则进入下一步。
• 同步更新（注意要同步更新，不能将更新过的$\theta$带入计算接下来的$\theta$）:
  $${\theta }_i={\theta }_i–\alpha \frac{\partial }{\partial {\theta }_i}J({\theta }_0,{\theta }_1\dots ,{\theta }_n)$$
  结束后，返回第一步。

矩阵描述

…

梯度下降变种

Batch Gradient Descent（BGD）

$${\theta }_i={\theta }_i–\alpha \sum _{j=0}^m(h_{\theta }(x_0^j,x_1^j,\dots x_n^j)–y_j)x_i^j$$

Stochastic Gradient Descent（SGD）

随机梯度下降法，其实和批量梯度下降法原理类似，区别在与求梯度时没有用所有的m个样本的数据，而是仅仅选取一个样本j来求梯度。对应的更新公式是：

$${\theta }_i={\theta }_i–\alpha h_{\theta }(x_0^j,x_1^j,\dots x_n^j)–y_j)x_i^j$$

随机梯度下降法，和批量梯度下降法是两个极端，一个采用所有数据来梯度下降，一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意。对于准确度来说，随机梯度下降法用于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。对于收敛速度来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。

小批量梯度下降法是一个中庸的办法能够结合两种方法的优点。

Mini-batch Gradient Descent（MBGD）

此变种调和了BGD和SGD矛盾，得到了更加中庸的方法，也就是对于m个样本，我们采用k个样子来迭代，1 $${\theta }_i={\theta }_i–\alpha \sum _{j=t}^{t_k-1}(h_{\theta }(x_0^j,x_1^j,\dots x_n^j)–y_j)x_i^j$$

Normal Equation

使用矩阵表示方程，可以使用解析方法来直接解出目标值：$\theta =(X^{T}X{)}^{-1}{X}^{T}y$

例子：
$m=4$

$x_0$	Size($fee{t}^2$) $x_1$	Number of bedrooms $x_2$	Number of floors $x_3$	Age of home(years) $x_4$	Price(1000 刀) $y$
1	2104	5	1	45	460
1	1416	3	2	40	232
1	1534	3	2	30	315
1	852	2	1	36	178

$$\begin{gathered} X=\left[\begin{array}{ccccccccccccccccc}1& 2104& 5& 1& 45 \\ 1& 1416& 3& 2& 40 \\ 1& 1534& 3& 2& 30 \\ 1& 852& 2& 1& 36\end{array}\right] \end{gathered}$$

$$\begin{gathered} y=\left[\begin{array}{c}460 \\ 232 \\ 315 \\ 178\end{array}\right] \end{gathered}$$

$$\theta =(X^{T}X{)}^{-1}{X}^{T}y$$

如果一个矩阵$(X^{T}X)$不可逆：

• Redundant features, where two features are very closely related (i.e. they are linearly dependent)
• Too many features (e.g. m ≤ n). In this case, delete some features or use “regularization” (to be explained in a later lesson).

Solutions to the above problems include deleting a feature that is linearly dependent with another or deleting one or more features when there are too many features.

多元线性回归

$x^(i)_j = $value of feature $j$ in the $i^{t}h$ training example
$x^{(}i)=$the column vector of all the feature inputs of the $i^{t}h$ training example
$m=$the number of training examples
$n=\mid \mid x^{(}i)\mid \mid ;$(the number of features)

hypothesis function:

$$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3+\cdots +{\theta }_n{x}_n$$

设有$x_0^{(}i)=1$，则：

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲h_\theta(x) =\b…

训练样例以row-wise储存在X中，$x_0^{(}i)=1$使得下列计算相对方便一些:

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲X = \begin{bmat…

$$h_{\theta }(X)=X\theta$$

多元线性回归的梯度下降

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲& \text{repeat …

Feature Scaling

如果样本项之间的范围相差过大，可能造成cost function的轮廓图呈扁平状态，从而导致梯度下降效率低下，下降路线可能会成密集的锯齿状。于是，我们是用Feature Scaling来将项目缩放到相似的区域：

feature scaling：dividing the input values by the range (i.e. the maximum value minus the minimum value) of the input variable, resulting in a new range of just 1.（1是不重要的，只要在这个数量级均可。）

mean normalization : 使用下列公式缩放：
$$x_i:=\frac{x_i-{\mu }_i}{s_i}$$
${\mu }_i$是所有特征i的平均值，$s_i$是范围或者标准差。

Feature Combine & Polynomial Regression

有时候不一定要使用某一个给定的feature，而是可以将若干个feature结合起来，比如将$x_1、x_2$结合为$x_1\cdot x_2$。

hypothesis function不一定要是线性的，可以使用quadratic, cubic or square root function (or any other form).
比如：

quadratic function：$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_1^2$

cubic function：$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_1^2+{\theta }_3{x}_1^3$

square root function:$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2\sqrt{x_1}$

使用Feature Combine，feature范围就很重要了

eg. if $x_1$ has range $1-1000$ then range of $x_1^2$ becomes $1-1000000$ and that of $x_1^3$ becomes $1-1000000000$.

逻辑回归

对于分类问题，有时候可以使用线性回归来进行拟合，通过大于0.5是1，小于等于就是0来实现。但是这种方法对于非线性函数工作的不好。

把y变成若干离散值，成为逻辑回归问题，它和线性回归很类似。

Binary classification problem

Hypothesis function

我们使用"Sigmoid Function," also called the “Logistic Function”:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-14xnJ6VA-1605237127062)(https://github.com/wubugui/FXXKTracer/raw/master/pic/Logistic_function.png)]

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲& h_\theta (x) …

$h_{\theta }(x)$给出了输出1的概率:

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲& h_\theta(x) =…

hypothesis function指使了下列性质：

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲& h_\theta(x) \…

并且：

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲& g(z) \geq 0.5…

同时：

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲z=0, e^{0}=1 \R…

因此我们可以检查$g(x)$中的x，来得到函数结果，也就是：
KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲& \theta^T x \g…

如果我们指定$g(x)$中的$x=0$，则得到了decision boundary方程，这条边界将数据区域分为$y=0$,$y=1$两个区域。

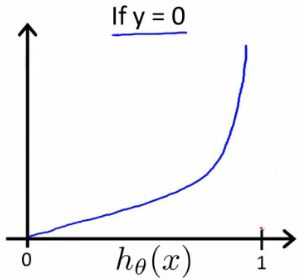
Cost Function

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲& J(\theta) = \…

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VeA7EmSR-1605237127063)(https://github.com/wubugui/FXXKTracer/raw/master/pic/Logistic_regression_cost_function_positive_class.png)]

几条性质：

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲& \mathrm{Cost}…

可以把两个Cost函数合成一个：

$$\mathrm{C}\mathrm{o}\mathrm{s}\mathrm{t}(h_{\theta }(x),y)=-y\log (h_{\theta }(x))-(1-y)\log (1-h_{\theta }(x))$$

最终整个J就如下：

$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log (h_{\theta }(x^{(i)}))+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))]$$

向量化：

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲ & h = g(X\thet…

此函数的梯度下降公式和线性回归的梯度下降公式具有相同的形式：

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲ & Repeat \; \l…

向量化：

$$\theta :=\theta -\frac{\alpha }{m}{X}^T(g(X\theta )-y)$$

We still have to simultaneously update all values in theta.

实现

使用matlab实现以下cost函数和梯度(注意正确的向量化)：

%X包含1，theta包含x0
ldm =  lambda/m;
dm = ldm/lambda;
m1 = length(theta);
sig = sigmoid(X*theta);
grad = dm.*X'*(sig - y) + ldm.*theta;
 %第一项求导没有尾巴，需要把尾巴减掉
grad(1,:) = grad(1,:) -  ldm*theta(1,:);
 %注意cost的最后规则化求和里面不包括第一项，所以theta0求导没有最后一个尾巴
J = -dm.*(log(sig)'*y+log(1-sig)'*(1-y)) + ldm*0.5* sum(theta(2:m1,:).^2);
%return J,grad

%训练一组预测num_label个数字的参数
function [all_theta] = oneVsAll(X, y, num_labels, lambda)
    m = size(X, 1);n = size(X, 2);
    all_theta = zeros(num_labels, n + 1);
    X = [ones(m, 1) X];
    initial_theta = zeros(n + 1, 1);
    options = optimset('GradObj', 'on', 'MaxIter', 50);
    for i=1:num_labels
         %y==i为逻辑数组
         [theta] = fmincg (@(t)(lrCostFunction(t, X, (y == i),  lambda)),initial_theta, options);
         %返回的是列向量
         all_theta(i,:) = theta';
    end
end

%预测
function p = predictOneVsAll(all_theta, X)
    m = size(X, 1);
    num_labels = size(all_theta, 1);
    p = zeros(size(X, 1), 1);
    X = [ones(m, 1) X];
    Mat = all_theta*X';
    for i=1:m
        [~,pos] = max(Mat(:,i));
        p(i,:) = pos;
    end
end

%Training Set Accuracy: 94.960000

向量化应该思考为：在矩阵里面逐元素操作。

高级优化

首先需要提供函数计算：

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲ & J(\theta) \n…

octave代码类似下面这样(这个没在matlab测试过，可能函数会有些不同)：

function [jVal, gradient] = costFunction(theta)
  jVal = [...code to compute J(theta)...];
  gradient = [...code to compute derivative of J(theta)...];
end

使用"fminunc()"优化算法（这个函数用于最小值优化也就是求最小值）：

options = optimset('GradObj', 'on', 'MaxIter', 100);
initialTheta = zeros(2,1);
   [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

Multiclass Classification: One-vs-all

把Binary classification拓展到Multiclass Classification，如果有$y=1,2,3,...,n$，就将问题分成n个Binary classification.

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲& y \in \lbrace…

We are basically choosing one class and then lumping all the others into a single second class. We do this repeatedly, applying binary logistic regression to each case, and then use the hypothesis that returned the highest value as our prediction.

Overfitting问题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PSWZ7gAb-1605237127067)(https://github.com/wubugui/FXXKTracer/raw/master/pic/0cOOdKsMEeaCrQqTpeD5ng_2a806eb8d988461f716f4799915ab779_Screenshot-2016-11-15-00.23.30.png)]

上图展示分别是underfitting，normal，overfitting的情况。

Underfitting, or high bias, is when the form of our hypothesis function h maps poorly to the trend of the data. It is usually caused by a function that is too simple or uses too few features.

At the other extreme, overfitting, or high variance, is caused by a hypothesis function that fits the available data but does not generalize well to predict new data. It is usually caused by a complicated function that creates a lot of unnecessary curves and angles unrelated to the data.

This terminology is applied to both linear and logistic regression. There are two main options to address the issue of overfitting:

1. Reduce the number of features:

• 手动选择feature保留。
• Use a model selection algorithm

2. Regularization

• 保持所有的features, 但是减少参数θj的值.
• Regularization works well 当我们有大量影响甚微的features时.

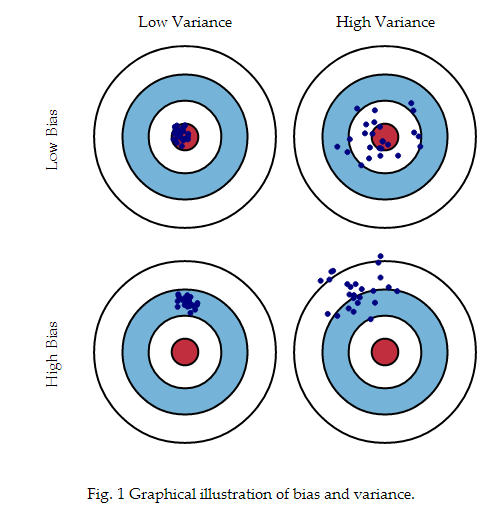
Error due to Variance ： 在给定模型数据上预测的变化性，你可以重复整个模型构建过程很多次，variance 就是衡量每一次构建模型预测相同数据的变化性。图形上，如图所示，图形中心是模型完美正确预测数据值，当我们远离中心预测越来越差，我们可以重复整个模型构建过程多次，通过每一次命中图形来表示bias and variance：

???

规则化后的线性回归

使用规则化后的Cost函数：

$$mi{n}_{\theta }\frac{1}{2m}\left[\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+\lambda \sum _{j=1}^n{\theta }_j^2\right]$$

$\lambda$具有平滑原来函数的效果，并且越大平滑效果越好。

新的梯度下降：

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲ & \text{Repeat…

后者也可以写为：
$${\theta }_j:={\theta }_j(1-\alpha \frac{\lambda }{m})-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$

Normal Equation变为：

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲& \theta = \lef…

规则化后的逻辑回归

Cost函数：

$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log (h_{\theta }(x^{(i)}))+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$

新加入的和式意味着惩罚bias term。

梯度下降：

KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲ & \text{Repeat…

神经网络

基本概念

神经输入电信号channel到输出。在神经网络中，输入的feature$x_1...x_n$就是神经的输入信号，输出信号是hypothesis function的输出，注意这里输出的是一个函数，和前面的内容差不多。

$x_0$叫做“bias unit”，总是等于1.
使用前面classification中相同的logistic function$\frac{1}{1+e^{\theta T_x}}$,这叫做sigmoid (logistic) activation.这里面的$\theta$就叫做weights.

神经网络一个非常简单的表示：

$$\begin{gathered} \left[\begin{array}{c}{x}_0 \\ {x}_1 \\ {x}_2 \\ \end{array}\right]\to \left[\begin{array}{c} \\ \end{array}\right]\to h_{\theta }(x) \end{gathered}$$

输入节点（layer 1）叫做“输入层”，这一层输入到（layer 2），最终输出hypothesis function，叫做“输出层”。
$[]$所包含的是“隐藏层”。这些内部隐藏层表示为：

$$\begin{gathered} \left[\begin{array}{c}{x}_0 \\ {x}_1 \\ {x}_2 \\ {x}_3\end{array}\right]\to \left[\begin{array}{ccccccc}{a}_1^{(2)}& ...& a_1^{(n)} \\ {a}_2^{(2)}& ...& a_2^{(n)} \\ {a}_3^{(2)}& ...& a_2^{(n)} \\ \end{array}\right]\to h_{\theta }(x) \end{gathered}$$

其中，$a_i^{(j)}$叫做"activation units"，中的i表示第几个单位，j表示层数。

为了把地j层映射到j+1层，使用权重矩阵${\Theta }^j$.
$$\begin{gathered} \left[\begin{array}{cccccccccc}{\Theta }_{10}^{(1)}& {\Theta }_{11}^{(1)}& {\Theta }_{12}^{(1)}& {\Theta }_{13}^{(1)} \\ {\Theta }_{20}^{(1)}& {\Theta }_{21}^{(1)}& {\Theta }_{22}^{(1)}& {\Theta }_{23}^{(1)} \\ {\Theta }_{30}^{(1)}& {\Theta }_{31}^{(1)}& {\Theta }_{32}^{(1)}& {\Theta }_{33}^{(1)}\end{array}\right] \end{gathered}$$

注意：左乘矩阵

每一项${\Theta }_{ts}^l$中，t表示映射目标unit，s表示要作用的源输入，l表示来自哪一层。

神经网络
$$\begin{gathered} \left[\begin{array}{c}{x}_0 \\ {x}_1 \\ {x}_2 \\ {x}_3\end{array}\right]\to \left[\begin{array}{c}{a}_1^{(2)} \\ {a}_2^{(2)} \\ {a}_3^{(2)} \\ \end{array}\right]\to h_{\theta }(x) \end{gathered}$$
的映射关系展开如下：

KaTeX parse error: No such environment: align at position 7: \begin{̲a̲l̲i̲g̲n̲}̲ a_1^{(2)} = g(…

如果神经网络的第$j$层有$s_j$个单位，第$j+1$层有$s_{j+1}$个单位，那么映射矩阵维度为：$s_{j+1}\times (s_j+1)$(也就是$s_{j+1}$行$s_j+1$列)(左乘情形下).其中的$s_j+1$的$+1$来自于"bias nodes",$x_0$ and ${\Theta }_0^{(j)}$.

例子：
对如下网络使用权重矩阵${\Theta }^{(1)}=\left[\begin{array}{ccc}-10& 20& 20\end{array}\right]$可以得到$OR$函数。
KaTeX parse error: No such environment: align at position 7: \begin{̲a̲l̲i̲g̲n̲}̲\begin{bmatrix}…
${\Theta }^{(1)}=\left[\begin{array}{ccc}-30& 20& 20\end{array}\right]$可以得到$AND$函数。

Multiclass Classification

将输出的元素搞成不止一个单元，也就是映射到$R^n$来处理多维分类问题。

简单实现

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Wnk9g4ho-1605237127069)(https://github.com/wubugui/FXXKTracer/raw/master/pic/nn.png)]

前面实现了使用逻辑回归的多类分类器，但是逻辑回归不能表示更复杂的hypothesis function，只能实现线性分类器。
现在先使用已经训练好的参数来实现前馈传播算法（feedforward propagation algorithm）。

function p = predict(Theta1, Theta2, X)
    m = size(X, 1);
    num_labels = size(Theta2, 1);
    p = zeros(size(X, 1), 1);
    l = ones(m,1);
    X = [l,X];
    A = Theta1*X';
    A = sigmoid(A)';
    A = [l,A];
    A = Theta2*A';
    A = sigmoid(A);
    [~,p] = max(A',[],2);
    %就是做矩阵乘法然后在结果中挑一个值最大的，位置即为值，矩阵转置过来转置过去可能性能很低。
end

Cost Function

$$J(\Theta )=-\frac{1}{m}\sum _{i=1}^m\sum _{k=1}^K[y_k^{(i)}\log ((h_{\Theta }(x^{(i)}){)}_k)+(1-y_k^{(i)})\log (1-(h_{\Theta }(x^{(i)}){)}_k)]+\frac{\lambda }{2m}\sum _{l=1}^{L-1}\sum _{i=1}^{s_l}\sum _{j=1}^{s_{l+1}}({\Theta }_{j,i}^{(l)}{)}^2$$

• $L$:网络总层数.
• $s_l$:第l层中不包括bias unit的单元数.
• $K$:Number of output units/classes.

Note:

• the double sum simply adds up the logistic regression costs calculated for each cell in the output layer
• the triple sum simply adds up the squares of all the individual Θs in the entire network.
• the i in the triple sum does not refer to training example i.

后向传播求梯度

目标是计算${\min }_{\Theta }J(\Theta )$，先计算$J(\Theta )$的梯度：
$$\frac{\partial }{\partial {\Theta }_{i,j}^{(l)}}J(\Theta )$$

使用下列Back propagation Algorithm：

• Given training set $\{(x^{(1)},y^{(1)})\cdots (x^{(m)},y^{(m)})\}$

• set ${\Delta }_{i,j}^{(l)}:=0$ for all (l,i,j), (hence you end up having a matrix full of zeros)

• For training example t =1 to m:

  • Set $a^{(1)}:=x^{(t)}$
  • Perform forward propagation to compute $a^{(l)}$ for l=2,3,…,L.(已经给定了一组假定的权重)
  • Using $y^{(t)}$,compute ${\delta }^{(L)}=a^{(L)}-y^{(t)}$（输出节点和训练数据的差就是$\delta$,然后逐步往前求每一层的$\delta$）
  • Compute ${\delta }^{(L-1)},{\delta }^{(L-2)},\dots ,{\delta }^{(2)}$ using ${\delta }^{(l)}=(({\Theta }^{(l)}{)}^T{\delta }^{(l+1)}).＊a^{(l)}.＊(1-a^{(l)})$(其中后面.＊的是$g^{\prime }(z^{(l)})=a^{(l)}.\ast (1-a^{(l)})$)
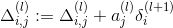  • or with vectorization,[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CR59eElQ-1605237127072)(https://github.com/wubugui/FXXKTracer/raw/master/pic/CodeCogsEqn.gif)]

• Hence we update our new $\Delta$ matrix.

  • ,if j != 0
  • [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-V3nKLFg4-1605237127074)(https://github.com/wubugui/FXXKTracer/raw/master/pic/CodeCogsEqn_2.gif)],otherwise.

• Finally,$\frac{\partial }{\partial {\Theta }_{ij}^{(l)}}J(\Theta )=D_{i,j}^{(l)}$.

理解

If we consider simple non-multiclass classification (k = 1) and disregard regularization, the cost is computed with:
$$cost(t)=y^{(t)}\log (h_{\Theta }(x^{(t)}))+(1-y^{(t)})\log (1-h_{\Theta }(x^{(t)}))$$
$${\delta }_j^{(l)}=\frac{\partial }{\partial z_j^{(l)}}cost(t)$$
Recall that our derivative is the slope of a line tangent to the cost function, so the steeper the slope the more incorrect we are. Let us consider the following neural network below and see how we could calculate some${\delta }_j^{(l)}$.
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-M17VKIkd-1605237127075)(https://github.com/wubugui/FXXKTracer/raw/master/pic/qc309rdcEea4MxKdJPaTxA_324034f1a3c3a3be8e7c6cfca90d3445_fixx.png)]
In the image above, to calculate ${\delta }_2^{(2)}$,we multiply the weights
${\Theta }_{12}^{(2)}$ and ${\Theta }_{22}^{(2)}$ by their respective $\delta$ values found to the right of each edge. So we get ${\delta }_2^{(2)}={\Theta }_{22}^{(2)}{\delta }_1^{(3)}+{\Theta }_{22}^{(2)}{\delta }_2^{(3)}$.To calculate every single possible ${\delta }_j^{(l)}$ ,we could start from the right of our diagram. We can think of our edges as our ${\Theta }_{ij}$.Going from right to left, to calculate the value of ${\delta }_j^{(l)}$ ,you can just take the over all sum of each weight times the $\delta$ it is coming from. Hence, another example would be ${\delta }_2^{(3)}={\Theta }_{12}^{(3)}\ast {\delta }_1^{(4)}$
** “error term”${\delta }_j^{(l)}$ 通俗点说表示这一个节点应该为最后输出的误差负多少责。**

实现

将矩阵展平为向量thetaVec = [Theta1(:);Theta2(:);Theta3(:)];
从向量中提取矩阵reshape(thetaVec(1:110),10,11);将thetaVec的前110个元素提取为10行，11列的矩阵。
在实现的时候，将传递展平为向量的矩阵。

神经网络方向传播算法比较复杂，计算出来的结果可以使用下列方法来Check梯度计算是否正确：

使用当时的$\Theta$带入下式：
$$\frac{\partial }{\partial {\Theta }_j}J(\Theta )\approx \frac{J({\Theta }_1,\dots ,{\Theta }_j+ϵ,\dots ,{\Theta }_n)-J({\Theta }_1,\dots ,{\Theta }_j-ϵ,\dots ,{\Theta }_n)}{2ϵ}$$

一般$ϵ=10^{-4}$.
这种方法可以近似计算梯度，但是及其的缓慢，所以check完之后注意关闭。

随机初始化$\Theta$的时候，需要打破对称，并且在区间$[-{ϵ}_{init},{ϵ}_{init}]$均匀随机选择。对于${ϵ}_{init}$的选择，一般可以准守如下规则：

One effective strategy for choosing ${ϵ}_{init}$ is to base it on the number of units in the network. A good choice of ${ϵ}_{init}$ is ${ϵ}_{init}=\frac{\sqrt{6}}{\sqrt{L_{in}+L_{out}}}$ ,where $L_{in}=s_l$ and $L_{out}=s_{l+1}$ are the number of units in the layers adjacent to ${\Theta }^{(l)}$.

function [J grad] = nnCostFunction(nn_params, ...
                                   input_layer_size, ...
                                   hidden_layer_size, ...
                                   num_labels, ...
                                   X, y, lambda)
% for our 2 layer neural network
Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)), ...
                 hidden_layer_size, (input_layer_size + 1));

Theta2 = reshape(nn_params((1 + (hidden_layer_size * (input_layer_size + 1))):end), ...
                 num_labels, (hidden_layer_size + 1));
m = size(X, 1);
J = 0;
Theta1_grad = zeros(size(Theta1));
Theta2_grad = zeros(size(Theta2));
l = ones(m,1);
%加一列bais
Xn = [l,X];
Z1 = Xn';
A1 = Xn';
%已经有了bais的参数
A = Theta1*Xn';
Z2 = A;
A = sigmoid(A);
A = [l,A'];
A2 = A';
A = Theta2*A';
Z3 = A;
A3 = A;
A = sigmoid(A);
%1列一组数据

ldm =  lambda/m;
dm = ldm/lambda;
%y为1x10
%m lines
%装换y格式
p = randperm(num_labels);
p = sort(p);
yn = p(ones(m,1),:);
for idx=1:m
    yn(idx,:) = yn(idx,:)==y(idx);
end
a = diag(yn*log(A));
b = diag((1.-yn)*log(1.-A));
J= -sum(a+b)/m;

[n1,n] = size(Theta1);
k1 = 0;
for i=1:n1
    for j=2:n
        k1= k1+Theta1(i,j)*Theta1(i,j);
    end
end

[n1,n] = size(Theta2);
k2 = 0;
for i=1:n1
    for j=2:n
        k2=k2+Theta2(i,j)*Theta2(i,j);
    end
end
J=J+(k1+k2)*ldm*0.5;

%Backpropagation
for i=1:m
    delta3 = A(:,i) - yn(i,:)';
    delta2 = Theta2'*delta3.*sigmoidGradient([1;Z2(:,i)]);
    Theta1_grad = Theta1_grad + (A1(:,i)*delta2(2:end)')';
    temp = A2(:,i)*delta3';
    Theta2_grad = Theta2_grad + temp';
end

Theta1_grad = Theta1_grad./m;
Theta2_grad = Theta2_grad./m;

[~,n2]=size(Theta1);
Theta1_grad(:,2:n2) = Theta1_grad(:,2:n2) + ldm*Theta1(:,2:n2);
[~,n2]=size(Theta2);
Theta2_grad(:,2:n2) = Theta2_grad(:,2:n2) + ldm*Theta2(:,2:n2);
% Unroll
grad = [Theta1_grad(:) ; Theta2_grad(:)];
end

Advice for Applying Machine Learning & Machine Learning System Design

训练学习曲线

训练不同的数量的example得到的参数用来训练一组cross validation数据，并与自身对比误差。

function [error_train, error_val] = ...
    learningCurve(X, y, Xval, yval, lambda)
    m = size(X, 1);
    error_train = zeros(m, 1);
    error_val   = zeros(m, 1);
    for i=1:m
        %learning theta
        t = trainLinearReg(X(1:i,:),y(1:i,:),lambda);
        %train
        [j,~]=linearRegCostFunction(X(1:i,:), y(1:i,:), t, 0);
        error_train(i)=j;
        %cross validation
        [j,~]=linearRegCostFunction(Xval, yval, t, 0);
        error_val(i)=j;
    end
end

……未完待续

支持向量机

用一个比较直观的图来理解支持向量机：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tTiKeJd3-1605237127076)(https://github.com/wubugui/FXXKTracer/raw/master/pic/mm_svm.png)]
首先要注意：多项式${\Theta }^{T}X$可以理解为向量的内积。向量的内积可以写为$|{\Theta }^T||X|cos<{\Theta }^T,X>=|{\Theta }^T|Pr{j}_{{\Theta }^T}X$.
上图中${\Theta }_n$代表训练参数，$L_{{\Theta }_n}$代表分类直线，其中${\Theta }_n$指向直线的法向，可以看到，M点和G点分别做到各个${\Theta }_n$的投影，得到$P_n,P_n^{\prime }$.
此时SVM要求求解：
$$mi{n}_{\Theta }\frac{1}{2}\sum _{j=1}^n{\theta }_j^2=mi{n}_{\Theta }\frac{1}{2}|\Theta {|}^2$$
s.t.
$p^{(i)}|\theta|\ge 1 $if $y^{(i)}=1$
$p^{(i)}|\theta|\le -1 $if $y^{(i)}=0$
为了简化，已经令${\theta }_0=0$.
这里的$p^{(i)}$就是上面$|X|$在${\Theta }^T$的投影.
现在，要解决这个最优化问题，就要令$\theta$最小，但又要满足上述条件，那么一方面就要$|p^{(i)}|$非常大，那么也就意味着投影要非常小，也就是说X必须距离$L_{{\Theta }_n}$这条线远越好，所以，这个条件将让$X$尽量地远离分割直线，也就形成了一个边缘。。另一方面结合上图$L_{{\Theta }_1}$和$L_{{\Theta }_2}$以及对应的两个数据$G,M$来看，可以获得数据是如何被分类的直觉。

核方法

之前我们有hypothesis function多项式：
$$h_{\theta }(X)=X\theta ={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3+\cdots +{\theta }_n{x}_n$$
后来可以将这些项变为：
quadratic function：$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_1^2$
cubic function：$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_1^2+{\theta }_3{x}_1^3$
square root function:$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2\sqrt{x_1}$
现在这些可以写为：
$$h_{\theta }(f(X))={\theta }_0+{\theta }_{1}f(x_1)+{\theta }_{2}f(x_2)+{\theta }_{3}f(x_3)+\cdots +{\theta }_{n}f(x_n)$$
这样的写法获得更多灵活性，$f$被称为核(Kernel).
比如为了度量相似度可以使用高斯核：
$$f_1=\exp (-\frac{\Vert x_1-l^{(1)}\Vert }{2{\sigma }^2})$$

所以优化函数变为：
$$mi{n}_{\theta }C\sum _{i=1}^m{y}^{(i)}cos{t}_1({\Theta }^T{f}^{(i)})+(1-y^{(i)})cos{t}_0({\Theta }^T{f}^{(i)})+\frac{1}{2}\sum _{j=1}^m{\theta }_j^2$$

参数选择

对于参数$C=\frac{1}{\lambda }$，大C低偏高方差，小C反之。
参数${\sigma }^2$,大，$f_i$平滑，高偏，低方差。
大量example小feature用高斯函数，小数据直接线性，高斯容易overfit.
另外依然要注意数据feature的归一化。

参数选择目标：选择参数和核函数，以便在cross-validation数据上执行得最好。

选择

n=number of features,m=number of training examples

• If n is large (relative to m):
  使用逻辑回归或者线性核SVM

• if n is small ,m is intermediate:
  使用高斯核SVM

• if n is small,m is large:
  创建/添加更多features，然后使用逻辑回归或者线性核SVM

• 神经网络可能对所有上述设定都工作的良好，但是可能会更慢。

无监督学习

K-means算法

概述：

先给k个cluster中心，然后寻找距离中心最近的数据，把这些数据平均后，得到新的cluster中心，再将对应的那个cluter中心移动到新得到的clusetr中心，重复上述过程直到最后cluster中心收敛不动。

算法流程：

• 随机初始化K cluster中心$\mu_1,\mu_2,…,\mu_K \in \mathbb{R}^n $
• 循环直到所有的cluster中心不动
  • for i= 1 to m
    - $c^{(i)}$:=index(from 1 to K) of cluster centroid closest to $x^{(i)}$
    for k = 1 to K
    - ${\mu }_k$:=average (mean) of points assigned to cluster $k$

其中第一个循环叫做cluster assignment ：

$c^{(i)}$：训练example $x^{(i)}$所属的cluster（1,2,3，…,K）索引。
${\mu }_k$：第k个cluster中心。
${\mu }_{c^{(i)}}$：example $x^{(i)}$所属的cluster。

核心优化目标：

$$J(c^{(1)},...,c^{(m)},{\mu }_1,...,{\mu }_K)=\frac{1}{m}\sum _{i=1}^m||x^{(i)}-{\mu }_{c^{(i)}}|{|}^2$$

$$\underset{c^{(1)},...,c^{(m)},{\mu }_1,...,{\mu }_K}{\min }J(c^{(1)},...,c^{(m)},{\mu }_1,...,{\mu }_K)$$

It is not possible for the cost function to sometimes increase.If so,bug must be in the code.

第二部叫做move centroid.

初始化K

• K应该小于m（训练数据量）
• 从训练数据中随机选择K

局部最优

为了避免得到局部最优解，可以尝试跑50到100次下列算法：

• 随机初始化K
• 运行K-means算法，得到优化后的$c$和$\mu$
• 计算cost函数

最后选择使得cost函数最小的那一组$c,\mu$作为结果。

选择cluster的数目

肘部法则，下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ATgt8IFJ-1605237127077)(https://github.com/wubugui/FXXKTracer/raw/master/pic/ml_select_K.png)]

但是第二张图选择将会遇到一些困难。

值得一说的是，上图如果需要增长点，则可能说明增长点找到了一个局部最优值，需要重新使用多次随机初始化来得到最优的结果。

有时候，应用目的可能帮助你选择K值。比如生产T恤，决定SML三个型号的大小。

应用

K-mean可以将数据归类为更少的类别，也能用于数据压缩。比如，将一个真彩色图片压缩为一张16色图片。

实现

function centroids = computeCentroids(X, idx, K)
%COMPUTECENTROIDS returns the new centroids by computing the means of the 
%data points assigned to each centroid.
%   centroids = COMPUTECENTROIDS(X, idx, K) returns the new centroids by 
%   computing the means of the data points assigned to each centroid. It is
%   given a dataset X where each row is a single data point, a vector
%   idx of centroid assignments (i.e. each entry in range [1..K]) for each
%   example, and K, the number of centroids. You should return a matrix
%   centroids, where each row of centroids is the mean of the data points
%   assigned to it.
%

% Useful variables
[m n] = size(X);

% You need to return the following variables correctly.
centroids = zeros(K, n);


% ====================== YOUR CODE HERE ======================
% Instructions: Go over every centroid and compute mean of all points that
%               belong to it. Concretely, the row vector centroids(i, :)
%               should contain the mean of the data points assigned to
%               centroid i.
%
% Note: You can use a for-loop over the centroids to compute this.
%

for k=1:K
    s = [0,0];
    n = 0;
    for i=1:m
        index = idx(i,:);
        if index==k
            centroids(k,:) = centroids(k,:) + X(i,:);
            n = n + 1;
        end
    end
    centroids(k,:) = centroids(k,:)/(n);
end



% =============================================================


end


function centroids = kMeansInitCentroids(X, K)
%KMEANSINITCENTROIDS This function initializes K centroids that are to be 
%used in K-Means on the dataset X
%   centroids = KMEANSINITCENTROIDS(X, K) returns K initial centroids to be
%   used with the K-Means on the dataset X
%

% You should return this values correctly
centroids = zeros(K, size(X, 2));

% ====================== YOUR CODE HERE ======================
% Instructions: You should set centroids to randomly chosen examples from
%               the dataset X
%


randidx = randperm(size(X, 1));

centroids = X(randidx(1:K), :);




% =============================================================

end


function idx = findClosestCentroids(X, centroids)
%FINDCLOSESTCENTROIDS computes the centroid memberships for every example
%   idx = FINDCLOSESTCENTROIDS (X, centroids) returns the closest centroids
%   in idx for a dataset X where each row is a single example. idx = m x 1 
%   vector of centroid assignments (i.e. each entry in range [1..K])
%

% Set K
K = size(centroids, 1);

% You need to return the following variables correctly.
idx = zeros(size(X,1), 1);

% ====================== YOUR CODE HERE ======================
% Instructions: Go over every example, find its closest centroid, and store
%               the index inside idx at the appropriate location.
%               Concretely, idx(i) should contain the index of the centroid
%               closest to example i. Hence, it should be a value in the 
%               range 1..K
%
% Note: You can use a for-loop over the examples to compute this.
%


m = size(X,1);
for i = 1:m
    min_v = 99999;
    min_index = 0;
    for k=1:K
        A = X(i,:)-centroids(k,:);
        t = A*A';
        if t

数据维度压缩：将冗余数据降维，通俗的说是把n维数据，投影到n-1维超平面上。另外，有时候为了可视化数据和更好的理解，可能需要将数据降维到2D或者3D。

主成分分析（PCA）

简单地说，PCA将会找一个最合适的超平面（或者更低的维度），将所有数据投影上去，达到降低数据维度的目的。

线性回归和PCA有差别，线性回归最小化的是函数值的距离，而PCA是值到超平面（或更低维度）的距离。

借助函数库PCA的过程非常简单：

• 预处理数据：减去所有数据的均值，如果不同的feature具有不同的范围，则缩放到可比较的范围。
• 计算协方差矩阵$\Sigma =\frac{1}{m}{\sum }_{i=1}^n(x^{(i)})(x^{(i)}{)}^T$,计算协方差矩阵的特征向量，可使用[U,~,~]=svd(Sigma);.
• 取特征向量前k列，乘到X上得到结果矩阵。Ureduce = U(:,1:k);z=Ureduce'*X;

具体的数学推到参考PCA算法.

如果要重建原始数据，就使用这个矩阵将结果转换回去，但是不会得到精确值，因为在压缩的时候已经丢失了数据。但对于降维数据，本来就十分接近超平面，还原值几乎是相等的。

选择reduce的目标k值

一般选择k的目标是选择让以下式子最小的k：

$$\frac{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}-x_{approx}^{(i)}|{|}^2}{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}|{|}^2}$$

一般使得：

$$\frac{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}-x_{approx}^{(i)}|{|}^2}{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}|{|}^2}\le 0.01$$

如此保留了99%的差异性（retained variance）。

可以使用以下算法达到目标：

• 使用k=1,2,3,4,5…计算PCA
• 计算$U_{reduce},z^{(1)},z^{(2)},...,z^{(m)},x_{approx}^{(1)},...,x_{approx}^{(m)}$
• 测试结果是否满足目标

实际上，使用奇异值分解([U,S,V]=svd(sigma);)后，得到的S是一个对角矩阵（S_{ii}）为对角元素，而对角元素和目标有如下关系：

$$1-\frac{{\sum }_{i=1}^k{S}_{ii}}{{\sum }_{i=1}^n{S}_{ii}}=\frac{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}-x_{approx}^{(i)}|{|}^2}{\frac{1}{m}{\sum }_{i=1}^m||x^{(i)}|{|}^2}$$

所以在计算的时候只需要计算一次svd分解，使用不同的k计算$1-\frac{{\sum }_{i=1}^k{S}_{ii}}{{\sum }_{i=1}^n{S}_{ii}}$就可以了。

应用PCA的建议

PCA可以用来减少feature加速训练效率，但是使用PCA来减少feature以避免过拟合不是一个好主意。

实现

function [U, S] = pca(X)
%PCA Run principal component analysis on the dataset X
%   [U, S, X] = pca(X) computes eigenvectors of the covariance matrix of X
%   Returns the eigenvectors U, the eigenvalues (on diagonal) in S
%

% Useful values
[m, n] = size(X);

% You need to return the following variables correctly.
U = zeros(n);
S = zeros(n);

% ====================== YOUR CODE HERE ======================
% Instructions: You should first compute the covariance matrix. Then, you
%               should use the "svd" function to compute the eigenvectors
%               and eigenvalues of the covariance matrix. 
%
% Note: When computing the covariance matrix, remember to divide by m (the
%       number of examples).
%



Sigma = X'*X./m;
[U,S,~] = svd(Sigma);


% =========================================================================

end

function Z = projectData(X, U, K)
%PROJECTDATA Computes the reduced data representation when projecting only 
%on to the top k eigenvectors
%   Z = projectData(X, U, K) computes the projection of 
%   the normalized inputs X into the reduced dimensional space spanned by
%   the first K columns of U. It returns the projected examples in Z.
%

% You need to return the following variables correctly.
Z = zeros(size(X, 1), K);

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the projection of the data using only the top K 
%               eigenvectors in U (first K columns). 
%               For the i-th example X(i,:), the projection on to the k-th 
%               eigenvector is given as follows:
%                    x = X(i, :)';
%                    projection_k = x' * U(:, k);
%

%n*n
U_reduce = U(:,1:K);
%n*k
Z = X*U_reduce;


% =============================================================

end

function X_rec = recoverData(Z, U, K)
%RECOVERDATA Recovers an approximation of the original data when using the 
%projected data
%   X_rec = RECOVERDATA(Z, U, K) recovers an approximation the 
%   original data that has been reduced to K dimensions. It returns the
%   approximate reconstruction in X_rec.
%

% You need to return the following variables correctly.
X_rec = zeros(size(Z, 1), size(U, 1));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the approximation of the data by projecting back
%               onto the original space using the top K eigenvectors in U.
%
%               For the i-th example Z(i,:), the (approximate)
%               recovered data for dimension j is given as follows:
%                    v = Z(i, :)';
%                    recovered_j = v' * U(j, 1:K)';
%
%               Notice that U(j, 1:K) is a row vector.
%               

X_rec = Z*U(:,1:K)';

% =============================================================

end

异常检测(Anomaly detection)

异常检测可以理解为：相对于已有的数据分布偏离较远的数据，只要被检数据的发生概率小于给定的$ϵ$则检测到异常。可以用于检测飞机引擎质量，网络用户异常行为等等。

高斯分布下的异常检测算法

假设有m个examples.

• 选择一些n个有可能异常的features $x_i$
• 估计出每个feature的高斯分布参数${\mu }_1,...,{\mu }_n,{\sigma }_1^2,...,{\sigma }_n^2$
  $${\mu }_i=\frac{1}{m}\sum _{i=1}^m{x}_j^{(i)}$$
  $${\sigma }_j^2=\frac{1}{m}\sum _{i=1}^m(x_j^{(i)}-{\mu }_j{)}^2$$
• 对于一个新的exmaple对于给定的对应features，可以计算$p(x)$:
  $$p(x)=\prod _{j=1}^{n}p(x_j;{\mu }_j,{\sigma }_j^2)=\prod _{i=1}^n\frac{1}{\sqrt{2\pi }{\sigma }_j}{e}^{-\frac{(x_j-{\mu }_j{)}^2}{2{\sigma }_j^2}}$$
  如果$p(x)<ϵ$则检测到异常.

评估异常检测算法

使用大量数据拟合高斯分布
在cross validation 和 test example中，预测异常。
注意，这是一个偏斜的测试集，正常的比异常的多得多，所以评估参数要使用之前的F-score.
可以尝试选择不同的$ϵ$使用cv结合F-score来更新，然后使用test集来最终评估算法。

异常检测与监督学习

异常检测：

• 具有非常小的的positive examples(y=1)(0~20 is common.)
• 有很多不同类型的异常，如果使用监督学习从不同的异常中来学习分辨异常是不现实的。
• 未来检测到的某个异常可能和之前检测到的所有异常都不一样。
• 欺诈检测、制造业检测（检测坏零件）、数据中心监控计算机…

监督学习：

• 大量的positive和negative example.
• 有足够大的positive来训练算法分辨positive的特征，每个positive（过去的和未来的）都具有共同属性(长得差不多)。
• 垃圾邮件分类、天气预测、癌症分类…

有时候，异常检测也能转化为监督学习，比如，在异常检测中，得到异常越来越多，于是可以变成了分类问题。

选择待检测feature

拿到数据首先画出数据的直方图，对于非标准形状的分布，也可当做之前高斯分布的方法来做，但是会提高误差。但一般可以对数据取$log(Ax+B)$的log多项式来把数据矫正为高斯分布。

一般，我们希望p对于正常数据很大，对于异常很小。如果我们发现异常检测算法违背了我们希望的初衷，可以创建（选择）添加一个不大不小的feature。

应用

电影推荐系统

• $n_u$用户数量
• $n_m$电影数量
• $r(i,j)=1$如果用户j评价了电影i
• $y^{(i,j)}$用户j给电影i的评分

基于内容的推荐

假设每一步电影都有一个类型权.如《剑与勇士》动作0.9爱情0悬疑0.2等.

对于每个用户j，学习一组参数${\theta }^{(j)}$(作用于类型权，不要忘了x0=1)；预测用户j将会对电影i评分为$({\theta }^{(j)}{x}^{(i)}$。

同时计算所有的$\theta$
优化目标为（加上正则化term防止最优化结果过大）：

$$mi{n}_1{\theta }^{(1)},...,{\theta }^{(n_u)}\frac{1}{2}\sum _{j=1}^{n_u}\sum _{i:r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(i)}-y^{(i,j)}{)}^2+\frac{\lambda }{2}\sum _{j=1}^{n_u}\sum _{k=1}^n({\theta }_k^{(j)}{)}^2$$

梯度下降：

$${\theta }_k^{(j)}:={\theta }_k^{(j)}-\alpha \sum _{i:r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(}i)-y^{(i,j)})x_k^{(i)}$$ (k=0)

$${\theta }_k^{(j)}:={\theta }_k^{(j)}-\alpha \sum _{i:r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(}i)-y^{(i,j)})x_k^{(i)}+\lambda {\theta }_k^{(j)}$$ (k!=0)

协同过滤

很多时候我们并不知道每个电影的类型权是多少。我们需要通过用户提供的$\theta$来计算出这些特征权。

类似地我们把上面的优化目标换为$x^{(i)}$得到需要的优化目标。

所以给出$\Theta$可以求得$x^{(i)}$，给出$x^{(i)}$可以得到$\Theta$.

于是我们最开始随机猜测一个$\theta$然后不断地循环上面的过程，从而得到更好的特征作出更好的预测。

更好的方法是，将两个最优化过程同时进行合二为一:

Cost函数：

$$J(x^{(1)},...,x^{(n_m)},{\theta }^{(1),...,{\theta }^{(n_u)}})=\frac{1}{2}\sum _{(i,j):r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(i)}-y^{(i,j)}{)}^2+\frac{\lambda }{2}\sum _{i=1}^{n_m}\sum _{k=1}^n(x_k^{(i)}{)}^2+\frac{\lambda }{2}\sum _{i=1}^{n_m}\sum _{k=1}^n({\theta }_k^{(i)}{)}^2$$

最小化cost求参数$x$/$\theta$即可。

算法

• 随机初始化$x$和$\theta$
• 最小化J
• 对于用户${\theta }^{(j)}$和电影$x^{(i)}$，使用KaTeX parse error: Double superscript at position 13: \theta^{(j)}^̲T x^{(i)}计算评分

找出相关电影

最小化特征权的距离。

实现细节：Mean Normalization

给每部电影计算用户平均分，然后原始分减去平均分，再使用此进行协同过滤学习，最后在使用最小化结果计算用户对某部电影评分的时候加上这个平均分，这样就可以避免没有评价过电影的用户（$\theta$全是0）,得到一个全0的评分（这样的评分没有意义）。

实现

基本测试

%% Initialization
clear ; close all; clc

%% ================== Part 1: Load Example Dataset  ===================
%  We start this exercise by using a small dataset that is easy to
%  visualize.
%
%  Our example case consists of 2 network server statistics across
%  several machines: the latency and throughput of each machine.
%  This exercise will help us find possibly faulty (or very fast) machines.
%

fprintf('Visualizing example dataset for outlier detection.\n\n');

%  The following command loads the dataset. You should now have the
%  variables X, Xval, yval in your environment
load('ex8data1.mat');

%  Visualize the example dataset
plot(X(:, 1), X(:, 2), 'bx');
axis([0 30 0 30]);
xlabel('Latency (ms)');
ylabel('Throughput (mb/s)');

fprintf('Program paused. Press enter to continue.\n');
pause


%% ================== Part 2: Estimate the dataset statistics ===================
%  For this exercise, we assume a Gaussian distribution for the dataset.
%
%  We first estimate the parameters of our assumed Gaussian distribution, 
%  then compute the probabilities for each of the points and then visualize 
%  both the overall distribution and where each of the points falls in 
%  terms of that distribution.
%
fprintf('Visualizing Gaussian fit.\n\n');

%  Estimate my and sigma2
[mu sigma2] = estimateGaussian(X);

%  Returns the density of the multivariate normal at each data point (row) 
%  of X
p = multivariateGaussian(X, mu, sigma2);

%  Visualize the fit
visualizeFit(X,  mu, sigma2);
xlabel('Latency (ms)');
ylabel('Throughput (mb/s)');

fprintf('Program paused. Press enter to continue.\n');
pause;

协同过滤与推荐系统

%% =============== Part 1: Loading movie ratings dataset ================
%  You will start by loading the movie ratings dataset to understand the
%  structure of the data.
%  
fprintf('Loading movie ratings dataset.\n\n');

%  Load data
load ('ex8_movies.mat');

%  Y is a 1682x943 matrix, containing ratings (1-5) of 1682 movies on 
%  943 users
%
%  R is a 1682x943 matrix, where R(i,j) = 1 if and only if user j gave a
%  rating to movie i

%  From the matrix, we can compute statistics like average rating.
fprintf('Average rating for movie 1 (Toy Story): %f / 5\n\n', ...
        mean(Y(1, R(1, :))));

%  We can "visualize" the ratings matrix by plotting it with imagesc
imagesc(Y);
ylabel('Movies');
xlabel('Users');

fprintf('\nProgram paused. Press enter to continue.\n');
pause;

%% ============ Part 2: Collaborative Filtering Cost Function ===========
%  You will now implement the cost function for collaborative filtering.
%  To help you debug your cost function, we have included set of weights
%  that we trained on that. Specifically, you should complete the code in 
%  cofiCostFunc.m to return J.

%  Load pre-trained weights (X, Theta, num_users, num_movies, num_features)
load ('ex8_movieParams.mat');

%  Reduce the data set size so that this runs faster
num_users = 4; num_movies = 5; num_features = 3;
X = X(1:num_movies, 1:num_features);
Theta = Theta(1:num_users, 1:num_features);
Y = Y(1:num_movies, 1:num_users);
R = R(1:num_movies, 1:num_users);

%  Evaluate cost function
J = cofiCostFunc([X(:) ; Theta(:)], Y, R, num_users, num_movies, ...
               num_features, 0);
           
fprintf(['Cost at loaded parameters: %f '...
         '\n(this value should be about 22.22)\n'], J);

fprintf('\nProgram paused. Press enter to continue.\n');
pause;


%% ============== Part 3: Collaborative Filtering Gradient ==============
%  Once your cost function matches up with ours, you should now implement 
%  the collaborative filtering gradient function. Specifically, you should 
%  complete the code in cofiCostFunc.m to return the grad argument.
%  
fprintf('\nChecking Gradients (without regularization) ... \n');

%  Check gradients by running checkNNGradients
checkCostFunction;

fprintf('\nProgram paused. Press enter to continue.\n');
pause;


%% ========= Part 4: Collaborative Filtering Cost Regularization ========
%  Now, you should implement regularization for the cost function for 
%  collaborative filtering. You can implement it by adding the cost of
%  regularization to the original cost computation.
%  

%  Evaluate cost function
J = cofiCostFunc([X(:) ; Theta(:)], Y, R, num_users, num_movies, ...
               num_features, 1.5);
           
fprintf(['Cost at loaded parameters (lambda = 1.5): %f '...
         '\n(this value should be about 31.34)\n'], J);

fprintf('\nProgram paused. Press enter to continue.\n');
pause;


%% ======= Part 5: Collaborative Filtering Gradient Regularization ======
%  Once your cost matches up with ours, you should proceed to implement 
%  regularization for the gradient. 
%

%  
fprintf('\nChecking Gradients (with regularization) ... \n');

%  Check gradients by running checkNNGradients
checkCostFunction(1.5);

fprintf('\nProgram paused. Press enter to continue.\n');
pause;


%% ============== Part 6: Entering ratings for a new user ===============
%  Before we will train the collaborative filtering model, we will first
%  add ratings that correspond to a new user that we just observed. This
%  part of the code will also allow you to put in your own ratings for the
%  movies in our dataset!
%
movieList = loadMovieList();

%  Initialize my ratings
my_ratings = zeros(1682, 1);

% Check the file movie_idx.txt for id of each movie in our dataset
% For example, Toy Story (1995) has ID 1, so to rate it "4", you can set
my_ratings(1) = 4;

% Or suppose did not enjoy Silence of the Lambs (1991), you can set
my_ratings(98) = 2;

% We have selected a few movies we liked / did not like and the ratings we
% gave are as follows:
my_ratings(7) = 3;
my_ratings(12)= 5;
my_ratings(54) = 4;
my_ratings(64)= 5;
my_ratings(66)= 3;
my_ratings(69) = 5;
my_ratings(183) = 4;
my_ratings(226) = 5;
my_ratings(355)= 5;

fprintf('\n\nNew user ratings:\n');
for i = 1:length(my_ratings)
    if my_ratings(i) > 0 
        fprintf('Rated %d for %s\n', my_ratings(i), ...
                 movieList{i});
    end
end

fprintf('\nProgram paused. Press enter to continue.\n');
pause;


%% ================== Part 7: Learning Movie Ratings ====================
%  Now, you will train the collaborative filtering model on a movie rating 
%  dataset of 1682 movies and 943 users
%

fprintf('\nTraining collaborative filtering...\n');

%  Load data
load('ex8_movies.mat');

%  Y is a 1682x943 matrix, containing ratings (1-5) of 1682 movies by 
%  943 users
%
%  R is a 1682x943 matrix, where R(i,j) = 1 if and only if user j gave a
%  rating to movie i

%  Add our own ratings to the data matrix
Y = [my_ratings Y];
R = [(my_ratings ~= 0) R];

%  Normalize Ratings
[Ynorm, Ymean] = normalizeRatings(Y, R);

%  Useful Values
num_users = size(Y, 2);
num_movies = size(Y, 1);
num_features = 10;

% Set Initial Parameters (Theta, X)
X = randn(num_movies, num_features);
Theta = randn(num_users, num_features);

initial_parameters = [X(:); Theta(:)];

% Set options for fmincg
options = optimset('GradObj', 'on', 'MaxIter', 100);

% Set Regularization
lambda = 10;
theta = fmincg (@(t)(cofiCostFunc(t, Ynorm, R, num_users, num_movies, ...
                                num_features, lambda)), ...
                initial_parameters, options);

% Unfold the returned theta back into U and W
X = reshape(theta(1:num_movies*num_features), num_movies, num_features);
Theta = reshape(theta(num_movies*num_features+1:end), ...
                num_users, num_features);

fprintf('Recommender system learning completed.\n');

fprintf('\nProgram paused. Press enter to continue.\n');
pause;

%% ================== Part 8: Recommendation for you ====================
%  After training the model, you can now make recommendations by computing
%  the predictions matrix.
%

p = X * Theta';
my_predictions = p(:,1) + Ymean;

movieList = loadMovieList();

[r, ix] = sort(my_predictions, 'descend');
fprintf('\nTop recommendations for you:\n');
for i=1:10
    j = ix(i);
    fprintf('Predicting rating %.1f for movie %s\n', my_predictions(j), ...
            movieList{j});
end

fprintf('\n\nOriginal ratings provided:\n');
for i = 1:length(my_ratings)
    if my_ratings(i) > 0 
        fprintf('Rated %d for %s\n', my_ratings(i), ...
                 movieList{i});
    end
end

function [bestEpsilon bestF1] = selectThreshold(yval, pval)
%SELECTTHRESHOLD Find the best threshold (epsilon) to use for selecting
%outliers
%   [bestEpsilon bestF1] = SELECTTHRESHOLD(yval, pval) finds the best
%   threshold to use for selecting outliers based on the results from a
%   validation set (pval) and the ground truth (yval).
%

bestEpsilon = 0;
bestF1 = 0;
F1 = 0;

stepsize = (max(pval) - min(pval)) / 1000;
for epsilon = min(pval):stepsize:max(pval)
    
    % ====================== YOUR CODE HERE ======================
    % Instructions: Compute the F1 score of choosing epsilon as the
    %               threshold and place the value in F1. The code at the
    %               end of the loop will compare the F1 score for this
    %               choice of epsilon and set it to be the best epsilon if
    %               it is better than the current choice of epsilon.
    %               
    % Note: You can use predictions = (pval < epsilon) to get a binary vector
    %       of 0's and 1's of the outlier predictions


predictions = (pval < epsilon);



tp = sum((predictions==1)&(yval==1));
fp = sum((predictions==1)&(yval==0));
fn = sum((predictions==0)&(yval==1));


prec = tp/(tp+fp);
rec = tp/(tp+fn);

F1 = 2*prec*rec/(prec+rec);





    % =============================================================

    if F1 > bestF1
       bestF1 = F1;
       bestEpsilon = epsilon;
    end
end

end

function [J, grad] = cofiCostFunc(params, Y, R, num_users, num_movies, ...
                                  num_features, lambda)
%COFICOSTFUNC Collaborative filtering cost function
%   [J, grad] = COFICOSTFUNC(params, Y, R, num_users, num_movies, ...
%   num_features, lambda) returns the cost and gradient for the
%   collaborative filtering problem.
%

% Unfold the U and W matrices from params
X = reshape(params(1:num_movies*num_features), num_movies, num_features);
Theta = reshape(params(num_movies*num_features+1:end), ...
                num_users, num_features);

            
% You need to return the following values correctly
J = 0;
X_grad = zeros(size(X));
Theta_grad = zeros(size(Theta));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost function and gradient for collaborative
%               filtering. Concretely, you should first implement the cost
%               function (without regularization) and make sure it is
%               matches our costs. After that, you should implement the 
%               gradient and use the checkCostFunction routine to check
%               that the gradient is correct. Finally, you should implement
%               regularization.
%
% Notes: X - num_movies  x num_features matrix of movie features
%        Theta - num_users  x num_features matrix of user features
%        Y - num_movies x num_users matrix of user ratings of movies
%        R - num_movies x num_users matrix, where R(i, j) = 1 if the 
%            i-th movie was rated by the j-th user
%
% You should set the following variables correctly:
%
%        X_grad - num_movies x num_features matrix, containing the 
%                 partial derivatives w.r.t. to each element of X
%        Theta_grad - num_users x num_features matrix, containing the 
%                     partial derivatives w.r.t. to each element of Theta
%


M = X*Theta'- Y;
T = M.*M;
J = sum(T(R==1))/2;

%regularized
l1 = 0;
for i=1:num_users
    for j=1:num_features
       l1=l1+Theta(i,j)*Theta(i,j);
    end
end
l1 = l1*0.5*lambda;

l2 = 0;
for i=1:num_movies
    for j=1:num_features
       l2=l2+X(i,j)*X(i,j);
    end
end
l2 = l2*0.5*lambda;

J = J + l1 + l2;
        

for i=1:num_movies
    idx = find(R(i,:)==1);
    tt = Theta(idx,:);
    yt = Y(i,idx);
    X_grad(i,:) = (X(i,:)*tt'-yt)*tt + lambda*X(i,:);
end


for i=1:num_users
    idx = find(R(:,i)==1);
    xt = X(idx,:);
    yt = Y(idx,i);
    %theta 1*f
    %theta_g u*f
    %xt idx*f
    %yt = idx*1
    Theta_grad(i,:) = (xt*Theta(i,:)'-yt)'*xt + lambda*Theta(i,:);
end



% =============================================================

grad = [X_grad(:); Theta_grad(:)];

end

function [mu sigma2] = estimateGaussian(X)
%ESTIMATEGAUSSIAN This function estimates the parameters of a 
%Gaussian distribution using the data in X
%   [mu sigma2] = estimateGaussian(X), 
%   The input X is the dataset with each n-dimensional data point in one row
%   The output is an n-dimensional vector mu, the mean of the data set
%   and the variances sigma^2, an n x 1 vector
% 

% Useful variables
[m, n] = size(X);

% You should return these values correctly
mu = zeros(n, 1);
sigma2 = zeros(n, 1);

for i = 1:n
    mu(i) = sum(X(:,i))/m;
    K = X(:,i)-mu(i);
    sigma2(i) = K'*K/m;
end
% =============================================================
end

课程总结

• 监督学习：线性回归，逻辑回归，神经网络，支持向量机
• 无监督学习：K-means，PCA，异常检测
• 特殊应用：推荐系统，大规模机器学习
• 构建机器学习系统的建议：偏与方差，规则化，决定接下来做什么工作，评估机器学习算法，学习曲线，误差分析，ceiling分析。

Ref

• https://www.coursera.org/learn/machine-learning
• http://www.52ml.net/20615.html
• http://blog.csdn.net/huruzun/article/details/41457433
• 深入理解机器学习：从原理到算法