图注意力神经网络(GAT)深度解析--论文+源码

前言

图神经网络(GNN)从大的线路可以划分为频域和空间域。频域的代表是图卷积神经网络(GCN),下一篇博文会介绍。在空间域方面，GAT作为经典的空间域GNN的代表模型，适合初入GNN的学者学习。空间域的GNN容易理解，不需要高深复杂的数学推导，从整体思想上很容易把握。《Graph Attention Networks》这篇文章是Bengio大佬团队出品，发表在ICLR2018，目前谷歌引用已经过千，很值得你品，细品。本人前后花了半个月左右的时间将论文和源码研读了一遍，现整理如下，供同行参考学习。本人也是初入深度学习大门，边看论文边补基础，python和TensorFlow也是现学现卖，如有理解错误，请留言或私信批评指正。

1 资源下载链接

1、论文：《Graph Attention Networks》
2、源码
（1）官方 TensorFlow 版
（2）Keras 版
（3）Pytorch 版
3、参考博文
(1)【GNN】图注意力网络GAT(含代码讲解)
(2) 深入理解图注意力机制
(3) 微信公众号 阿泽的学习笔记之【GNN】GAN：Attention 在 GNN 中的应用

2 论文解析

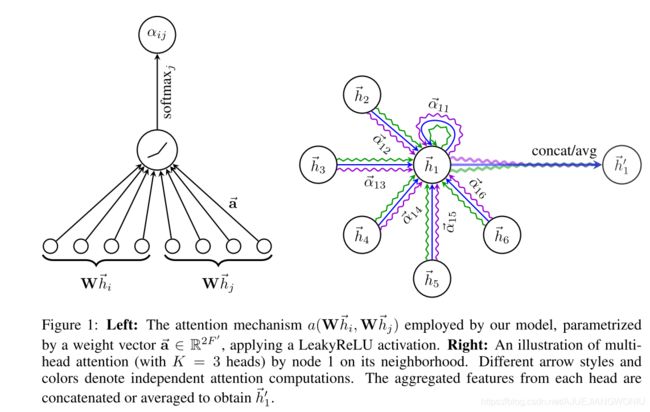
这篇文章的核心思想利用神经网络学习中心节点的各个邻居节点的权重因子，再通过学习到的权重因子乘以邻居节点的特征来聚合表征中心节点，以此来更新中心节点的特征。上图左侧为单个注意力机制，把投影后的中心节点和邻居节点通过LeakyReLU激活，再进行归一化得到注意力因子。右图为多个相互独立的注意力机制共同作用(图中有3个相互独立的注意力机制)，经过contact得到更新后的节点特征。

大家通过阅读论文后会发现，作者只会把创新点罗列其中。所以对于刚入门的同学来说，读起这篇文章觉得很费劲，不知道在讲什么，前后没有一个体系，觉得很虚。这篇论文就是介绍了如何将attention应用到图数据当中。在文中的数学讨论部分给出了6个公式，下面进行介绍。
$$e_{ij}=a(W{h}_i,W{h}_j)$$
上述公式表示利用注意力机制 a 得到节点 j 对于节点 i 的注意力因子 $e_{ij}$(该注意力因子是不对称的)。$h_i$,$h_j$分别表示节点 i 和 j 的特征表示，W是一个共享参数的权重矩阵。该公式允许图中所有的节点参与到表示中心节点的特征来，所以通过引入mask来把不是中心节点的邻居节点过滤掉。
为了使不同节点的注意力因子易于比较，作者通过引入softmaxt函数对其进行归一化处理：

$$a_{ij}=sofema{x}_j(e_{i,j})=\frac{exp(e_{ij})}{{\sum }_{k\in N_i}exp(e_{ik})}$$

k 表示 节点 i 的所有邻居节点。
在作者的实验中，注意力机制是一个单层的前向神经网络，引入权重向量 $a$ ,并应用LeakyReLU非线性单元，这样便得到了最后的注意力因子，可以表示为：

$$a_{ij}=\frac{exp(LeakyReLU(a^T[Whi||W{h}_j))}{{\sum }_{k\in N_i}exp((LeakyReLU(a^T[Whi||W{h}_j)))}$$

||表示一种拼接操作。
得到最后的注意力因子之后，再将其与对应的特征相乘求和，加上激活函数，就能够得到中心节点新的特征表示：

$$h_i^{,}=\sigma (\sum _{j\in N_i}{a}_{i,j}W{h}_j)$$
为了使注意力机制的学习过程更加稳定，作者引入了多头注意力机制。多头注意力机制可以这样理解，对于中心节点引入多个相互独立的注意力机制，得到不同的注意力矩阵，然后将利用不同的注意力矩阵得到的新特征拼接起来，公式如下：

$$h_i^{,}=|{|}_{K=1}^K\sigma (\sum _{j\in N_i}{a}_{i,j}^k{W}^k{h}_j)$$
K表示注意力机制的个数。
如果多头注意力机制在最后一层的话，需要对其求平均：

$$h_i^{,}=\frac{1}{K}\sigma (\sum _{k=1}^K\sum _{j\in N_i}{a}_{i,j}^k{W}^k{h}_j)$$

3 源码详解(TensorFlow 版)

我现在理解GAT在做的事情就是借助于邻接矩阵，通过权重矩阵聚合邻居节点的特征来更新中心节点的特征。

3.1 图注意力层

1、数据处理部分
实验部分的数据采用Cora数据集，存储在data文件夹里

各个文件里的数据解释如下： x.shape:(140, 1433)； y.shape:(140, 7);tx.shape:(1000, 1433);ty.shape:(1000, 1433); allx.shape:(1708, 1433);ally.shape:(1708, 7)。graph是一个字典，存储着各个节点连接的数据表示。数据处理的代码比较琐碎，主要捡几个比较重要的函数进行讲解：
首先是process.py下的load_data函数，这个函数主要是为了得到邻接矩阵，特征矩阵，各个标签矩阵和mask。这段代码几乎每行都进行了注释，数据的转换理解起来比较复杂。我认为在GNN中处理数据占了很重要的一部分工作，需要构造出特征矩阵和邻接矩阵。各位可以好好理解理解，多用print大法。

def load_data(dataset_str): # {'pubmed', 'citeseer', 'cora'}
    """Load data."""
    names = ['x', 'y', 'tx', 'ty', 'allx', 'ally', 'graph']
    #列表
    objects = []

    for i in range(len(names)):
        with open("data/ind.{}.{}".format(dataset_str, names[i]), 'rb') as f:
            #查看Python版本号
            if sys.version_info > (3, 0):
                objects.append(pkl.load(f, encoding='latin1'))
            else:
                objects.append(pkl.load(f))
    x, y, tx, ty, allx, ally, graph = tuple(objects)
    # x.shape:(140, 1433); y.shape:(140, 7);tx.shape:(1000, 1433);ty.shape:(1000, 1433);
    # allx.shape:(1708, 1433);ally.shape:(1708, 7)
    ##graph是一个字典，大图总共2708个节点
    
    # 测试数据集的索引乱序版
    test_idx_reorder = parse_index_file("data/ind.{}.test.index".format(dataset_str))#解析test数据集的序号文件
    #按行大小排序[1708 1709 ...2707],形状为(1000,)的一维向量
    test_idx_range = np.sort(test_idx_reorder)
   
    # 将allx和tx叠起来并转化成LIL格式的feature,即输入一张整图
    features = sp.vstack((allx, tx)).tolil()
    # print(features.shape)  #(2708,1433)
    # 把特征矩阵还原，和对应的邻接矩阵对应起来，因为之前是打乱的，不对齐的话，特征就和对应的节点搞错了。
    features[test_idx_reorder, :] = features[test_idx_range, :] #矩阵的切片操作，将后1000行赋值给前面
    # print(features.shape)   #(2708，1433)

    G1=nx.from_dict_of_lists(graph)#将列表构造成图
    adj = nx.adjacency_matrix(G1)#求出邻接矩阵的稀疏形式(稀疏矩阵的编码格式)

    #这就使得特征、邻接矩阵和标签一一对应了起来
    labels = np.vstack((ally, ty))
    labels[test_idx_reorder, :] = labels[test_idx_range, :]#矩阵的切片操作，将后1000行赋值给前面
    # print(labels.shape)  #(2708,7)
   
    idx_test = test_idx_range.tolist()#将np中的数组转换为Python中的列表
    # print(idx_test)
    # [1708, 1709, 1710, 1711, 1712, 1713,...,2705, 2706, 2707]
    # print(len(idx_test))
    # 1000
    idx_train = range(len(y))#140
    # print(idx_train)
    # range(0, 140)
    idx_val = range(len(y), len(y)+500)#140至640
    # print(idx_val,len(idx_val))
    # range(140, 640) 500

    # 训练mask：idx_train=[0,140)范围的是True，后面的是False
    train_mask = sample_mask(idx_train, labels.shape[0])
    # 验证mask：val_mask的idx_val=(140, 640]范围为True，其余的是False
    val_mask = sample_mask(idx_val, labels.shape[0])
    # test_mask，idx_test=[1708,2707]范围是True，其余的是False
    test_mask = sample_mask(idx_test, labels.shape[0])
   
    y_train = np.zeros(labels.shape)
    y_val = np.zeros(labels.shape)
    y_test = np.zeros(labels.shape)

    # 替换了true位置
    y_train[train_mask, :] = labels[train_mask, :]
    y_val[val_mask, :] = labels[val_mask, :]
    y_test[test_mask, :] = labels[test_mask, :]
    # print(y_train.shape," ",y_test.shape," ",y_val.shape)
    # (2708, 7)(2708, 7)(2708, 7)


    return adj, features, y_train, y_val, y_test, train_mask, val_mask, test_mask

train_mask，val_mask，test_mask是为了划分训练，验证和测试的。因为AX一次会得到所有节点的表示，但是计算loss只在部分节点上进行(参考[深入理解图注意力机制])。
在process.py文件下还有一个十分重要的函数adj_to_bias，该函数的作用是用一个很大的负数代替0元素，为什么做这个替换在深入理解图注意力机制有详细的说明，这里不再介绍。
2、图注意力层的构建
(1)注意力机制(重点)
注意力机制的实现是在layers.py下的attn_head函数里，同样我也给几乎每行代码进行了注释，如下所示：

def attn_head(seq, out_sz, bias_mat, activation, in_drop=0.0, coef_drop=0.0, residual=False):
    with tf.name_scope('my_attn'):
        if in_drop != 0.0:
            #防止过拟合，保留seq中1.0 - in_drop个数，保留的数并变为1/1.0 - in_drop
            seq = tf.nn.dropout(seq, 1.0 - in_drop)
        #将原始节点特征 seq 进行变换得到了 seq_fts。这里，作者使用卷积核大小为 1 的 1D 卷积模拟投影变换，
        # 投影变换后的维度为 out_sz。注意，这里投影矩阵 W是所有节点共享，所以 1D 卷积中的多个卷积核也是共享的。
        #seq_fts 的大小为 [num_graph, num_node, out_sz]
        seq_fts = tf.layers.conv1d(seq, out_sz, 1, use_bias=False) 

        # simplest self-attention possible
        # f_1 和 f_2 维度均为 [num_graph, num_node, 1]
        f_1 = tf.layers.conv1d(seq_fts, 1, 1)  #节点投影
        f_2 = tf.layers.conv1d(seq_fts, 1, 1)  #邻居投影

        #将 f_2 转置之后与 f_1 叠加，通过广播得到的大小为 [num_graph, num_node, num_node] 的 logits
        logits = f_1 + tf.transpose(f_2, [0, 2, 1])#注意力矩阵
        #+biase_mat是为了对非邻居节点mask,归一化的注意力矩阵
        #邻接矩阵的作用，把和中心节点没有链接的注意力因子mask掉
        coefs = tf.nn.softmax(tf.nn.leaky_relu(logits) + bias_mat)

        if coef_drop != 0.0:
            coefs = tf.nn.dropout(coefs, 1.0 - coef_drop)
        if in_drop != 0.0:
            seq_fts = tf.nn.dropout(seq_fts, 1.0 - in_drop)
         #将 mask 之后的注意力矩阵 coefs 与变换后的特征矩阵 seq_fts 相乘，
         # 即可得到更新后的节点表示 vals。
        vals = tf.matmul(coefs, seq_fts)
        ret = tf.contrib.layers.bias_add(vals)

        # residual connection
        if residual:
            if seq.shape[-1] != ret.shape[-1]:
                ret = ret + conv1d(seq, ret.shape[-1], 1) # activation
            else:
                ret = ret + seq

        return activation(ret)  # activation

通过注意力机制就可以得到更新后的节点特征。
如下是自己对整个过程的理解：

上图是利用权重矩阵得到更新后节点表示的过程,(图中的矩阵数据和维度只是为了表示说明整个过程，不代表任何意义)。假设图中有4个节点，每个节点有5个特征，这样就可以得到一个 4x5 的特征矩阵。通过神经网络学习可以得到一个 4x4 的权重矩阵(第一行表示节点1、2、3和4对节点1的权重分别为a+1,a+2,a+3和a+4)。再将对应的权重因子和其特征相乘便可以求得更新后的节点特征。上述过程就是注意力机制在做的事情。
（2）注意力层
该层的实现在gat.py文件夹里，在该层中作者取 K=8，利用了8个相互独立的注意力机制，且采用了8个隐层单元。具体实现不再废话。
重要的部分就这些，已讲完

3.2 定义损失、反向传播和训练

这部分无非就是神经网络的套路，如果对这些套路不清楚，那你就需要去补充机器学习的基础知识了
这部分的代码分别是在base_gattn.py下的loss和trainning函数里实现的。

我认为该篇文章的创新点在于把注意力机制引入到了对图数据的处理中来，并且通过神经网络学习出注意力矩阵。