K均值(K-means)聚类算法
文章目录
- 一、 K-Means原理
- 二、算法流程
-
- 2.1 算法描述
- 2.2 算法分析:
- 2.3 k-means评价标准
- 2.4 k-means优缺点
- 三、项目实战
K-Means算法是经典的无监督的聚类算法,它思想简单,实现起来比较方便,聚类效果也不错,因此应用很广泛。本文将讲解K-means聚类算法。
基本概念:
- 簇: 所有数据的点集合,簇中的对象是相似的。
- 质心: 簇中所有点的中心(计算所有点的均值而来)。
- SSE: Sum of Sqared Error(误差平方和), 它被用来评估模型的好坏,SSE 值越小,表示越接近它们的质心. 聚类效果越 好。由于对误差取了平方,因此更加注重那些远离中心的点(一般为边界点或离群点)。
一、 K-Means原理
思想:对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。
准则函数:聚类集中每一个样本点到该类中心的距离的平方之和,并使其最小化。
对所有k个模式类有:
J = ∑ j = 1 k ∑ i = 1 N j ∣ ∣ X i − Z j ∣ ∣ 2 , X i ∈ S j J=\sum_{j=1}^{k}\sum_{i=1}^{N_j}||X_i-Z_j||^2,X_i\in S_j J=j=1∑ki=1∑Nj∣∣Xi−Zj∣∣2,Xi∈Sj
S j S_j Sj:第 j 个聚类集,聚类中心为 Z j Z_j Zj ;
N j N_j Nj:第 j 个聚类集 S j S_j Sj 中所包含的样本个数。
目标:聚类中心的选择应使准则函数J极小,即:使 J j J_j Jj的极值最小,所以:
∂ J j ∂ Z j = 0 \frac{\partial J_j}{\partial Z_j}=0 ∂Zj∂Jj=0
即:
∂ ∂ Z j ∑ i = 1 N j ∣ ∣ X i − Z j ∣ ∣ 2 = ∂ ∂ Z j ∑ i = 1 N j ( X i − Z j ) T ( X i − Z j ) = 0 \frac{\partial}{\partial Z_j}\sum_{i=1}^{N_j}||X_i-Z_j||^2=\frac{\partial}{\partial Z_j}\sum_{i=1}^{N_j}(X_i-Z_j)^T(X_i-Z_j)=0 ∂Zj∂i=1∑Nj∣∣Xi−Zj∣∣2=∂Zj∂i=1∑Nj(Xi−Zj)T(Xi−Zj)=0
可解得:
Z j = 1 N j ∑ i = 1 N j X i , X i ∈ S j Z_j=\frac{1}{N_j}\sum_{i=1}^{N_j}X_i,X_i\in S_j Zj=Nj1i=1∑NjXi,Xi∈Sj
上式表明: S j S_j Sj类的聚类中心应选为该类样本的均值 。
如果我们想直接求上式的最小值并不容易,这是一个NP难的问题,因此只能采用启发式的迭代方法。
K-Means采用的启发式方式很简单,用下面一组图就可以形象的描述:
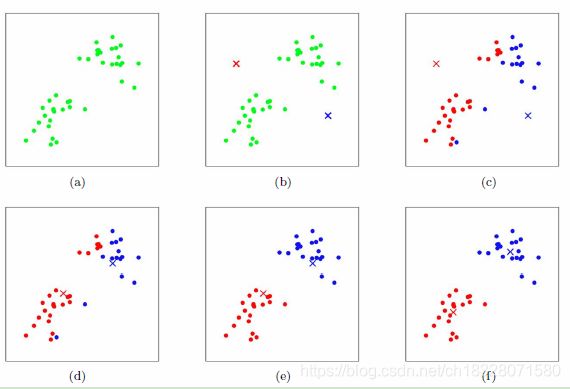
上图a表达了初始的数据集,假设k=2。在图b中,我们随机选择了两个k类所对应的类别质心,即图中的红色质心和蓝色质心,然后分别求样本中所有点到这两个质心的距离,并标记每个样本的类别为和该样本距离最小的质心的类别,如图c所示,经过计算样本和红色质心和蓝色质心的距离,我们得到了所有样本点的第一轮迭代后的类别。此时我们对我们当前标记为红色和蓝色的点分别求其新的质心,如图d所示,新的红色质心和蓝色质心的位置已经发生了变动。图e和图f重复了我们在图c和图d的过程,即将所有点的类别标记为距离最近的质心的类别并求新的质心。最终我们得到的两个类别如图f。
当然在实际K-Mean算法中,我们一般会多次运行图c和图d,才能达到最终的比较优的类别。
二、算法流程
2.1 算法描述
(1)任选K个初始聚类中心: Z 1 ( 1 ) Z_1(1) Z1(1), Z 2 ( 1 ) Z_2(1) Z2(1),… , Z k ( 1 ) Z_k(1) Zk(1)
括号内序号:迭代运算的次序号。
(2)按最小距离原则将其余样本分配到K个聚类中心中的某一个,即:
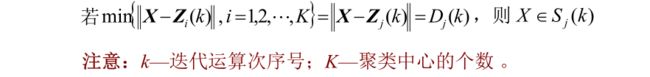
(3)计算各个聚类中心的新向量值: Z j ( k + 1 ) j = 1 , 2 , … , K Z_j(k+1) j=1,2,…,K Zj(k+1)j=1,2,…,K
Z j ( k + 1 ) = 1 N j ∑ X ∈ S j ( k ) X , j = 1 , 2 , . . . , K Z_j(k+1)=\frac{1}{N_j}\sum_{X\in S_j(k)}X,j=1,2,...,K Zj(k+1)=Nj1X∈Sj(k)∑X,j=1,2,...,K
N j N_j Nj:第 j 类的样本数
(4) 判断:
如果 Z j ( k + 1 ) ≠ Z j ( k ) , j = 1 , 2 , … , K Z_j(k+1) \neq Z_j(k),j = 1, 2, … , K Zj(k+1)̸=Zj(k),j=1,2,…,K, 则回到(2),将模式样本逐个中心分类,重复迭代计算。
如果 Z j ( k + 1 ) = Z j ( k ) , j = 1 , 2 , … , K Z_j(k+1)= Z_j(k), j = 1, 2, … , K Zj(k+1)=Zj(k),j=1,2,…,K, 算法收敛,计算完毕。
2.2 算法分析:
聚类结果受到所选聚类中心的个数和其初始位置,以及模式样本的几何性质及读入次序的影响。实际应用中需要试探不同的K值和选择不同的聚类中心起始值。
优点:
- 思想简单易行;
- 时间复杂度接近线性;
- 对大数据集,是可伸缩和有效的;
缺点:
- 要求事先给出要生成的簇数k, 不适合的k值可能返回较差的结果;
- 不适合发现非凸形状的簇,或者大小差别很大的簇;
- 对噪声和离群点敏感;
2.3 k-means评价标准
k-means算法因为手动选取k值和初始化随机质心的缘故,每一次的结果不会完全一样,而且由于手动选取k值,我们需要知道我们选取的k值是否合理,聚类效果好不好,将它们画在图上直接观察是比较直观的办法。但现实是,我们的数据不会仅仅只有两个特征,一般来说都有十几个特征,而观察十几维的空间对我们来说是一个无法完成的任务。因此,我们需要一个公式来帮助我们判断聚类的性能,这个公式就是SSE (Sum of Squared Error, 误差平方和 ),它其实就是每一个点到其簇内质心的距离的平方值的总和,这个数值对应kmeans函数中clusterAssment矩阵的第一列之和。 SSE值越小表示数据点越接近于它们的质心,聚类效果也越好。 因为对误差取了平方,因此更加重视那些远离中心的点。一种肯定可以降低SSE值的方法是增加簇的个数,但这违背了聚类的目标。聚类的目标是在保持簇数目不变的情况下提高簇的质量。
2.4 k-means优缺点
1)、优点:
- 属于无监督学习,无须准备训练集;
- 原理简单,实现起来较为容易;
- 结果可解释性较好;
2)、缺点:
- 聚类数目k是一个输入参数。选择不恰当的k值可能会导致糟糕的聚类结果。这也是为什么要进行特征检查来决定数据集的聚类数目了。
- 可能收敛到局部最小值, 在大规模数据集上收敛较慢
- 对于异常点、离群点敏感
使用数据类型 : 数值型数据
三、项目实战
项目实战请转至:tensorflow学习笔记(十二):K-means手写体数字(MNIST)识别。