kaggle 泰坦尼克 高分 预测

kaggle 泰坦尼克 高分 预测

1.前言

       在第一篇文章中我们简单介绍了一下泰坦尼克号数据如何使用机器学习的模型进行训练，通过船上人员的一些
  信息来预测该人是否可以生存，但是前面模型的构建中我们只是对数据做了一些简单的处理，并没有进行比较细致
  的特征提取，并且对于机器学习模型也没有对参数进行调整，所以本文将对上一篇文章进行改进，对数据进行更深
  入的特征提取和对模型参数进行调参的形式进行改进，改进之后，可以看到对测试集测试的准确率有了不错的提升。

2.包及数据导入

##包的导入
import pandas as pd
import numpy as np
import scipy.stats as ss
from sklearn.ensemble import RandomForestClassifier
from bayes_opt import BayesianOptimization
from sklearn.model_selection import cross_val_score
##数据的导入
train=pd.read_csv("./train.csv")##导入训练集
test=pd.read_csv("./test.csv")##导入测试集

3.数据的初步认识

接下来我们对数据的情况进行初步查看，首先我们对变量的个数和对应的数据类型进行查看,首先看训练集

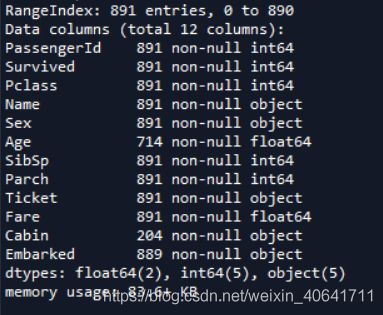
train.info()

结果如下：

可以看到训练集一共有12列数据，数据集中一共有891行数据，可以看到数据集有部分变量数据存在缺失，例如Age,Cabin,Embarked。数据类型一共有三种，浮点型，整型和字符串。接下来我们来看测试集数据的基本情况

test.info()

结果如下

可以看到测试集一共有11列数据 ，相比于训练集少了Survived变量，可以看到测试集也存在缺失数据，缺失数据主要在Age,Cabin,Fare三个变量之中。这些变量所对应的中文解释如下

变量名	中文解释
Survived	客户是否存活，该变量为该数据集中的因变量，其余为自变量
PassengerId	乘客ID
Pclass	代表乘客的阶级，数字越小阶级越高
Name	乘客姓名
Sex	性别
Parch	父母及子女的数量
SibSp	配偶及兄弟姐妹数量
Ticket	船票ID
Fare	票价
Cabin	乘客在船舱中的位置
Embarked	登船港口

在对数据有基本了解之后，接下来我们对训练数据和测试数据进行简单的统计分析

train.describe().drop("PassengerId",axis=1)
test.describe().drop("PassengerId",axis=1)

训练数据集结果如下

测试数据集结果如下

上面我们在数据集进行初步了解的过程中发现训练集和测试集均存在缺失数据，为了获取数据缺失的具体情况，我们对各变量的数据进行缺失数量统计

train.isna().sum(axis=0)
Out[15]: 
PassengerId      0
Survived         0
Pclass           0
Name             0
Sex              0
Age            177
SibSp            0
Parch            0
Ticket           0
Fare             0
Cabin          687
Embarked         2
dtype: int64

test.isna().sum(axis=0)
Out[16]: 
PassengerId      0
Pclass           0
Name             0
Sex              0
Age             86
SibSp            0
Parch            0
Ticket           0
Fare             1
Cabin          327
Embarked         0
dtype: int64

可以看到Cabin变量在训练集和测试集中均存在大量的缺失值。

4.数据关系的可视化

在做模型训练之前，对数据进行一定的可视化有助于观察数据之间的关系，可以为后续的特征工程做铺垫。
首先导入绘图用到的库

import matplotlib.pyplot as plt
import seaborn as sns

首先观察性别与幸存率的关系：可以看到女性幸存率远高于男性

plt.figure(dpi=200)
sns.barplot(x="Sex", y="Survived", data=train)

然后我们观察Pclass与幸存率的关系：可以看到乘客的阶级越高，幸存率越高

sns.barplot(x="Pclass", y="Survived", data=train)

观察SibSp与幸存率的关系：可以看到乘客配偶及兄弟姐妹数量适中的，幸存率更高

sns.barplot(x="SibSp", y="Survived", data=train)

观察Parch与幸存率的关系，发现父母与子女数适中的乘客幸存率更高

#Parch Feature：
sns.barplot(x="Parch", y="Survived", data=train)

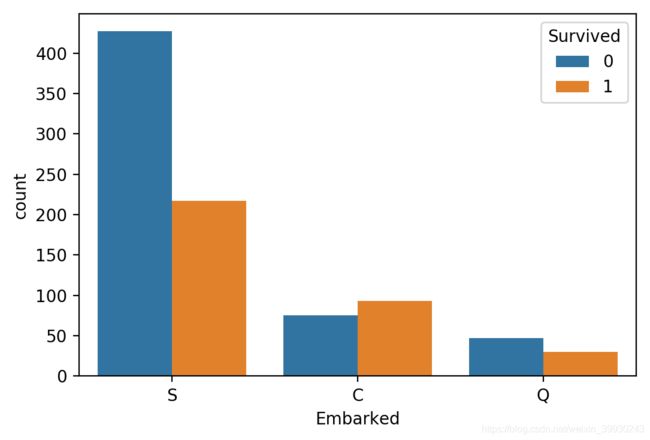
观察Embarked与幸存率的关系，结果发现:C地的生存率更高,这个也应该保留为模型特征.

sns.countplot('Embarked',hue='Survived',data=train)

观察年龄与幸存率的关系：
从不同生还情况的密度图可以看出，在年龄15岁的左侧，生还率有明显差别，密度图非交叉区域面积非常大，但在其他年龄段，则差别不是很明显，认为是随机所致，因此可以考虑将此年龄偏小的区域分离出来。

facet = sns.FacetGrid(train, hue="Survived",aspect=2)
facet.map(sns.kdeplot,'Age',shade= True)
facet.set(xlim=(0, train['Age'].max()))
facet.add_legend()
plt.xlabel('Age') 
plt.ylabel('density')

另外我们发现，不同称呼的乘客幸存率不同，所以我们新增Title特征，从姓名中提取乘客的称呼，归纳为六类，针对测试集的训练也可以考虑这一特征

train['Title'] = train['Name'].apply(lambda x:x.split(',')[1].split('.')[0].strip())
Title_Dict = {}
Title_Dict.update(dict.fromkeys(['Capt', 'Col', 'Major', 'Dr', 'Rev'], 'Officer'))
Title_Dict.update(dict.fromkeys(['Don', 'Sir', 'the Countess', 'Dona', 'Lady'], 'Royalty'))
Title_Dict.update(dict.fromkeys(['Mme', 'Ms', 'Mrs'], 'Mrs'))
Title_Dict.update(dict.fromkeys(['Mlle', 'Miss'], 'Miss'))
Title_Dict.update(dict.fromkeys(['Mr'], 'Mr'))
Title_Dict.update(dict.fromkeys(['Master','Jonkheer'], 'Master'))

train['Title'] = train['Title'].map(Title_Dict)
plt.figure(dpi=200)
sns.barplot(x="Title", y="Survived", data=train)

5.数据清洗与缺失值处理

接着我们进行数据清洗与缺失值处理，这一步最为重要的是对年龄进行处理，因为年龄的缺失是最多的，可以说，在这一步，对于年龄的处理是最为重要的。我们此前对于年龄的处理进行了多方面的尝试，我们试过直接使用均值，按照年龄和船票进行分组均值等多个方法。最后参考社区notebook使用名字对于年龄进行缺失值填充。这一思路初看是奇怪的，但深思之后发现其是合理的。我们的名字看似随机，实则深深受你出生时的时代所影响。像‘保国’‘建国’这种名字，毫无疑问是带有时代特征的，所以用名去匹配年龄是有其合理性存在的。

###对Age进行处理
data_all_2=pd.concat([train,test])
all_f_name=data_all_2.Name.apply(lambda x:(x.split(".")[1]).split(' ')[1])
all_f_name=all_f_name.str.replace('\(','',regex=True)
all_f_name=all_f_name.str.replace('\)','',regex=True)
all_fill_a=data_all_2["Age"].groupby(by=all_f_name).mean()[all_f_name[data_all_2["Age"].isna().values]].values.copy()
data_all_2["Age"][data_all_2.Age.isna()]=all_fill_a
data_all_2.Age=data_all_2.Age.fillna(data_all_2.Age.mean())
age_buckets= [0,2,10,18,60,200]
age_labels = [0,1,2,3,4]
data_all_2['Age'] = pd.cut(data_all_2['Age'], bins=age_buckets, labels=age_labels, right=False)

然后我们把家属关系转换为两个特征，一个表示家庭大小，一个表示是否独自上船。

train.Ticket=ticket2(train.Ticket.values)
train['Family']=train["SibSp"]+train['Parch']
train['Is_Alone']=train['Family'].apply(lambda x:1 if x==0 else 0)
test['Family']=test["SibSp"]+test['Parch']
test['Is_Alone']=test['Family'].apply(lambda x:1 if x==0 else 0)

除了年龄之外的可以使用的数据缺失值都不多，故简单进行填充即可。其中比较特殊的是Ability to bargain特征，它考量了一个人讨价还价的能力 。其他的地方都是些普通的数据清洗，就不再赘述了。

##对Parch进行处理
parch_buckets= [0,1,200]
parch_labels = [0,1]
data_all_2['Parch'] = pd.cut(data_all_2['Parch'], bins=parch_buckets, labels=parch_labels, right=False)

#对SibSp进行处理
sibsp_buckets= [0,1,200]
sibsp_labels = [0,1]
data_all_2['SibSp'] = pd.cut(data_all_2['SibSp'], bins=sibsp_buckets, labels=sibsp_labels, right=False)

#对Fare进行处理
fare_buckets= [0,23,10000]
fare_labels = [0,1]
data_all_2['Fare'] = data_all_2['Fare'].fillna(data_all_2['Fare'].mean())
data_all_2['Fare'] = pd.cut(data_all_2['Fare'], bins=fare_buckets, labels=fare_labels, right=False)

# Ability to bargain
#data_all_2['Fare'] = data_all_2['Fare'].astype(np.int8)
data_all_2['Pclass'] = data_all_2['Pclass'].astype(np.int8)


##构建Ability特征
data_all_2['Ability'] = data_all_2['Fare'].values/ data_all_2['Pclass'].values
ab_buckets= [0,4,9,15,20,59,70,10000]
ab_labels = [0,1,2,3,4,5,6]
data_all_2['Ability'] = pd.cut(data_all_2['Ability'], bins=ab_buckets, labels=ab_labels, right=False)


data_all_2=data_all_2.drop(['Embarked','Cabin'],axis=1)

train=data_all_2.iloc[0:train.shape[0],:]
test=data_all_2.iloc[train.shape[0]:,:]
test=test.drop("Survived",axis=1)



##对姓名进行处理
train.Name=train.Name.apply(lambda x :x.split(",")[1]).apply(lambda x :x.split(".")[0].lstrip())##获取名字中间信息
test.Name=test.Name.apply(lambda x :x.split(",")[1]).apply(lambda x :x.split(".")[0].lstrip())

6.数据的统计分析

我们对数据进行特征提取后，对提取的特征和因变量来进行显著性的检验。由于进行特征提取后的特征均为离散变量,我们对这些特征分别与因变量作卡方检验，查看其与因变量之间关系是否显著。

discrete_variable=["Pclass","Name","Sex","Is_Alone","Family","SibSp","Parch","Ticket","Ability","Age"]
y=train.Survived.values
result1=dict()
for i in discrete_variable:
    x=train[i].values
    t=table(x,y)
    kf = ss.chi2_contingency(t)
    result1[i]=[kf[1]]
    
result1=pd.DataFrame(result1)

结果如下

可以看到提取出来的特征与因变量进行卡方检验的p值均小于0.05，说明提取出来的特征与因变量之间有较强的显著性。

7.超参数优化

鉴于泰坦尼克预测项目的特征比较多，使用决策树算法很容易便产生了过拟合，在最终结果的预测上表现不佳。经过多次测试与总结，翻阅社区notebook的讨论，模型我们选定为随机森林模型。对于随机森林来说，我们所主要需要优化的超参数为：max_depth,min_samples_split,n_estimators。即最大深度，最小划分样本数目，与决策树数目。然后我们使用贝叶斯优化来对超参数进行调整。首先我们定义一个输入为参数，输出为交叉验证得分的函数function(m_p, m_s_s, n_s)，以及包含了参数范围的一个字典parameters

def rbt_optimization(cv_splits):
    def function(m_p, m_s_s, n_s):
            return cross_val_score(
                   RandomForestClassifier(
                   max_depth=max(0,int(m_p)), random_state=0,min_samples_split=max(0,int(m_s_s)),n_estimators=max(0,int(n_s))),  
                   X=train_x, 
                   y=train_y, 
                   cv=cv_splits,
                   scoring="roc_auc",
                   n_jobs=-1).mean()

    parameters = {"m_p": (1, 150),
                  "m_s_s": (2, 40),
                  "n_s": (10, 700)}
    
    return function, parameters

然后书写贝叶斯优化的主函数

def bayesian_optimization(dataset, function, parameters):
   train_x, train_y= dataset
   n_iterations = 100
   gp_params = {"alpha": 1e-4}

   BO = BayesianOptimization(function, parameters)
   BO.maximize(n_iter=n_iterations, **gp_params)

   return BO.max

接着我们开始进行超参优化：

dataset=[train_x,train_y]
f,p=rbt_optimization(2)
result1=bayesian_optimization(dataset, f, p)


#max_depth=147, random_state=0,min_samples_split=35,n_estimators=698

结果为#max_depth=147, random_state=0,min_samples_split=35,n_estimators=698

8.模型训练及结果输出

使用上文训练所获得的超参数，使用随机森林模型对结果进行预测，并存储于t2.csv

clf = RandomForestClassifier(max_depth=148, random_state=0,min_samples_split=39,n_estimators=288)##max_depth=30, random_state=0,min_samples_split=35,n=600
clf.fit(train_x,train_y)
y_p=clf.predict(test_x)
predict={}
predict['PassengerId']=P
predict['Survived']=y_p
result=pd.DataFrame(predict)
result.to_csv("./t2.csv",index=False)

.png")

9.总结

事实上我们比赛第一次提交的准确率只有0.74，排名也在1w4+，现在准确率有了0.8，排名也上升到了前5%。进一步做下去可能在该项目上获得的提升将十分有限，这将是我们目前关于kaggle 泰坦尼克项目的最后一次博客撰写。后续会转向其他的kaggle项目，同步继续产出博客，时间跨度大概为2-3周一篇。
在整个比赛中我们获益匪浅。除了通过具体项目去熟悉自己学习的机器学习方法，我们很大的一部分提升来自于kaggle的讨论区。阅读他人的笔记给我们起了很大的帮助，这也是我们希望分享自己的笔记的重要原因。
一个特别详细的kaggle笔记
使用集成方法的kaggle笔记
使用名字关联年龄特征的特征工程

10.贡献者介绍

我们是深大应用统计的在读研究生，希望通过项目的实践锻炼自身，后续会接着产出博客。除了评论区的交流，你还可以通过以下途径联系我们：
舒适黄狗，[email protected]
ZX,[email protected]
yzh, [email protected]