深度学习与自然语言处理教程(2) - GloVe及词向量的训练与评估（NLP通关指南·完结）

• 作者：韩信子@ShowMeAI
• 教程地址：https://www.showmeai.tech/tutorials/36
• 本文地址：https://www.showmeai.tech/article-detail/232
• 声明：版权所有，转载请联系平台与作者并注明出处
• 收藏ShowMeAI查看更多精彩内容

---

本系列为斯坦福CS224n《自然语言处理与深度学习(Natural Language Processing with Deep Learning)》的全套学习笔记，对应的课程视频可以在 这里 查看。

ShowMeAI为CS224n课程的全部课件，做了中文翻译和注释，并制作成了GIF动图！点击 这里 查看“第2讲-词向量进阶”的课件注释与带学解读。更多资料获取方式见文末。

---

引言

CS224n是顶级院校斯坦福出品的深度学习与自然语言处理方向专业课程，核心内容覆盖RNN、LSTM、CNN、transformer、bert、问答、摘要、文本生成、语言模型、阅读理解等前沿内容。

这组笔记首先介绍了训练词向量的Glove模型。然后，它扩展了我们对词向量(或称词嵌入)的讨论，看看它们是如何通过内部和外部来评估的。我们讨论了以词类比作为一种内在评价技术的例子，以及它如何被用来调整词嵌入技术。然后我们讨论了训练模型的权重/参数和词向量的外部任务。最后，我们将人工神经网络作为一种自然语言处理任务的模型。

内容要点

• Global Vectors for Word Representation (GloVe词向量)
• 词向量内部与外部评估方法
• 类比任务中的词向量训练超参数影响
• 相关度评估任务中词向量与人工表现差异
• 基于上下文处理一词多义问题
• 窗分类

1.GloVe词向量构建方法

1.1 对比前序方法

（GloVe方法的总结也可以参考ShowMeAI的对吴恩达老师课程的总结文章深度学习教程 | 自然语言处理与词嵌入）

到目前为止，我们已经研究了两类主要的词嵌入方法：

• 第一类方法是基于统计并且依赖矩阵分解(例如LSA，HAL)。虽然这类方法有效地利用了全局的信息，它们主要用于捕获单词的相似性，但是对例如单词类比的任务上表现不好。
• 第二类方法是基于浅层窗口(例如，Skip-Gram和CBOW 模型)，这类模型通过在局部上下文窗口通过预测来学习词向量。

这些模型除了在单词相似性任务上表现良好外，还展示了捕获复杂语言模式能力，但未能利用到全局共现统计数据。

相比之下，GloVe 由一个加权最小二乘模型组成，基于全局word-word共现计数进行训练，从而有效地利用全局统计数据。模型生成了包含有意义的子结构的单词向量空间，在词类比任务上表现非常出色。

❐ Glove利用全局统计量，以最小二乘为目标，预测单词 $j$ 出现在单词 $i$ 上下文中的概率。

1.2 共现矩阵

我们用 $X$ 表示word-word共现矩阵，其中 $X_{ij}$ 表示词 $j$ 出现在词 $i$ 的上下文的次数。令 $X_i={\sum }_k{X}_{ik}$ 为任意词 $k$ 出现在词 $i$ 的上下文的次数。最后，令 $P_{ij}=P(w_j\mid w_i)=\frac{X_{ij}}{X_i}$ 是词 $j$ 出现在词 $i$ 的上下文的概率。

计算这个矩阵需要遍历一次整个语料库获得统计信息。对庞大的语料库，这样的遍历会产生非常大的计算量，但是这只是一次性的前期投入成本。

❐ 共现矩阵 / Co-occurrence Matrix：

• $X$ ：word-word共现矩阵

• $X_{ij}$ ：词 $j$ 出现在词 $i$ 的上下文的次数

• $X_i={\sum }_k{X}_{ik}$ ：任意词 $k$ 出现在词 $i$ 的上下文的次数

• $P_{ij}=P(w_j\mid w_i)=\frac{X_{ij}}{X_i}$ ：词 $j$ 出现在词 $i$ 的上下文的概率

1.3 最小二乘目标函数

回想一下Skip-Gram模型，我们使用softmax来计算词 $j$ 出现在词 $i$ 的上下文的概率。

$$Q_{ij}=\frac{\exp (u_j^T{v}_i)}{{\sum }_{w=1}^W\exp (u_w^T{v}_i)}$$

训练时以在线随机的方式进行，但是隐含的全局交叉熵损失可以如下计算：

$$J=-\sum _{i\in corpus}\sum _{j\in context(i)}log{Q}_{ij}$$

同样的单词 $i$ 和 $j$ 可能在语料库中出现多次，因此首先将 $i$ 和 $j$ 相同的值组合起来更有效：

$$J=-\sum _{i=1}^W\sum _{j=1}^W{X}_{ij}log{Q}_{ij}$$

• 上面公式中，共现频率的值是通过共现矩阵 $X$ 给定。

交叉熵损失的一个显着缺点是要求分布 $Q$ 被正确归一化，因为对整个词汇的求和的计算量是非常大的。因此，我们使用一个最小二乘的目标函数，其中 $P$ 和 $Q$ 的归一化因子被丢弃了：

$$J=\sum _{i=1}^W\sum _{j=1}^W{X}_i(P_{ij}-Q_{ij}{)}^2$$

其中 $P_{ij}=X_{ij}$ 和 $Q_{ij}=\exp (u_j^T{v}_i)$ 是未归一化分布。这个公式带来了一个新的问题， $X_{ij}$ 经常会是很大的值，从而难以优化。一个有效的改变是最小化 $P$ 和 $Q$ 对数的平方误差：

$$\begin{array}{rl}J& =\sum _{i=1}^W\sum _{j=1}^W{X}_i{\left(\log (P{)}_{ij}-\log \left(Q_{ij}\right)\right)}^2\\ & =\sum _{i=1}^W\sum _{j=1}^W{X}_i{\left(u_j^T{v}_i-\log X_{ij}\right)}^2\end{array}$$

另外一个问题是权值因子 $X_i$ 不能保证是最优的。因此，我们引入更一般化的权值函数，我们可以自由地依赖于上下文单词：

$$J=\sum _{i=1}^W\sum _{j=1}^{W}f(X_{ij})(u_j^T{v}_i-\log X_{ij}{)}^2$$

1.4 GloVe模型结论

GloVe模型仅对单词共现矩阵中的非零元素训练，从而有效地利用全局统计信息，并生成具有有意义的子结构向量空间。给出相同的语料库，词汇，窗口大小和训练时间，它的表现都优于 word2vec，它可以更快地实现更好的效果，并且无论速度如何，都能获得最佳效果。

2.词向量评估

前面的内容介绍了Word2Vec和GloVe模型来训练和发现语义空间中的自然语言词语的潜在向量表示。下面我们来看看如何量化评估词向量的质量。

2.1 词向量内部评估

词向量的内部评估是对一组由如Word2Vec或GloVe生成的词向量在特定的中间子任务(如词类比)上的评估。这些子任务通常简单而且计算速度快，从而能够帮助我们理解生成的的词向量。内部评估通常应该返回给我们一个数值，来表示这些词向量在评估子任务上的表现。

• 对特定的中间任务进行评估
• 可以很快的计算性能
• 帮助理解子系统
• 需要和真实的任务正相关来确定有用性

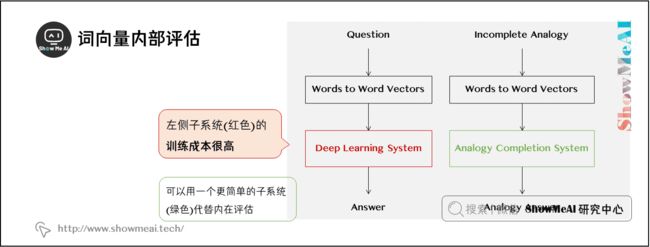
在下图中，左子系统(红色)训练的计算量大，因此更改为一个简单的子系统(绿色)作内部评估。

动机：我们考虑创建一个问答系统，其中使用词向量作为输入的例子。一个方法是训练一个机器学习系统：

• 1.输入词语
• 2.将输入词语转换为词向量
• 3.对一个复杂的机器学习系统，使用词向量作为输入
• 4.将输出的词向量通过系统映射到自然语言词语上。
• 5.生成词语作为答案

当然，在训练这样的一个问答系统的过程中，因为它们被用在下游子系统(例如深度神经网络)，我们需要创建最优的词向量表示。在实际操作中，我们需要对 Word2Vec 子系统中的许多超参数进行调整(例如词向量的维度)。

虽然最理想的方法是在 Word2Vec 子系统中的任何参数改变后都重新训练，但从工程角度来看是不实际的，因为机器学习系统(在第3步)通常是一个深层神经网络，网络中的数百万个参数需要很长的时间训练。

在这样的情况下，我们希望能有一个简单的内部评估技术来度量词向量子系统的好坏。显然的要求是内部评价与最终任务的表现有正相关关系。

❐ 内部评估

• 对特定的中间任务进行评估
• 可以很快的计算性能
• 帮助理解子系统
• 需要和真实的任务正相关来确定有用性

2.2 词向量外部评估

词向量的外部评估是对一组在实际任务中生成的词向量的评估。这些任务通常复杂而且计算速度慢。对我们上面的例子，允许对问题答案进行评估的系统是外部评估系统。通常，优化表现不佳的外部评估系统我们难以确定哪个特定子系统存在错误，这就需要进一步的内部评估。

• 对真实任务的评估
• 计算性能可能很慢
• 不清楚是子系统出了问题，还是其他子系统出了问题，还是内部交互出了问题
• 如果替换子系统提高了性能，那么更改可能是好的

2.3 内部评估示例：词类比

一个比较常用的内部评估的方法是词向量的类比。在词向量类比中，给定以下形式的不完整类比：

$$a:b::c:?$$

然后内部评估系统计算词向量的最大余弦相似度：

$$d=arg\underset{i}{\max }\frac{(x_b-x_a+x_c{)}^T{x}_i}{\Vert x_b-x_a+x_c\Vert }$$

❐ 注：我们看到单词向量包含单词间余弦距离的意义。它们还包含不同维度的含义：例如，“诺基亚”在某些维度上可能接近“三星”，因为它们都是电子公司，但在另一个维度上可能接近“芬兰”，因为不同的原因，诺基亚是芬兰公司。

❐ 注：当单词向量向下转换到2维(使用PCA)并用图形表示时，可以看到有趣的结果：相似的单词聚集在一起。然而，重要的是要记住，在降维过程中有相当一部分空间信息丢失了；因此，上面诺基亚示例中描述的单词之间的复杂关系可能不会出现。

这个指标有直观的解释。理想的情况下，我们希望 $x_b-x_a=x_d-x_c$ (例如，queen-king=actress-actor)。这就暗含着我们希望 $x_b-x_a+x_c=x_d$ 。因此，我们确定可以最大化两个词向量之间的归一化点积的向量 $x_d$ 即可(即余弦相似度)。使用诸如词向量类比的内部评估技术应该小心处理(要考虑到预训练的语料库的各个方面)。

例如，考虑以下的类比形式：

$$City1:StatecontainingCity1::City2:StatecontainingCity2$$

上图是可能受到具有相同名称的不同城市的语义词向量类比(内在评估)。在上面很多的例子，美国有很多同名的城市／城镇／村庄。因此，很多州都符合正确的答案。例如，在美国至少有10个地方的名称是Phoenix，所以Arizona不是唯一的正确答案。在考虑以下的类比形式：

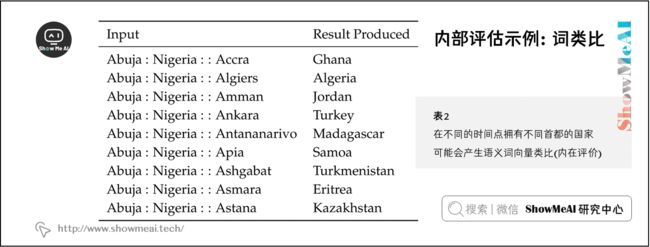
$$CapitalCity1:Country1::CapitalCity2:Country2$$

上图是可能在不同时间点有不同首都的国家的语义词向量类比(内在评估)。上面很多的例子，这个任务中生成的城市仅仅是近期的国家首都，可能会受到不同国家在不同时间点拥有不同首都的影响。例如，1997年之前Kazakhstan的首都是Almaty。因此，如果我们的语料库过时就会出现问题。

之前的两个例子说明如何使用词向量进行语义测试。我们也可以使用词向量类似进行语法测试。下面是测试形容词最高级概念的句法词向量类比(内在评价)，如下图所示：

类似地，下图的内部评估展示了测试词向量捕获过去时态概念的能力

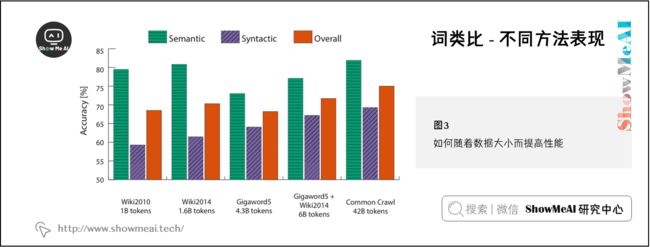
2.4 词类比-不同方法表现

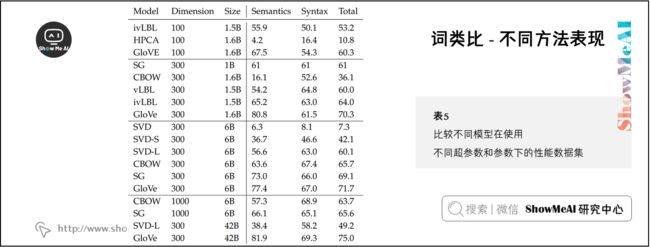
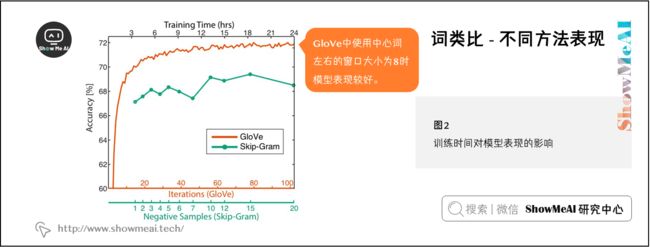
我们现在探讨使用内在评估系统(如类比系统)来调整的词向量嵌入技术(如Word2Vec和GloVe)中的超参数。我们首先来看看在类比评估任务中，在相同的超参数下，由不同方法创建的词向量表现效果：

根据上表，我们可以看到3点：

① 模型的表现高度依赖模型所使用的词向量的模型：

• 这点是可以预料到的，因为不同的生成词向量方法是基于不同的特性的(例如共现计数，奇异向量等等)。

② 语料库更大模型的表现更好：

• 这是因为模型训练的语料越大，模型的表现就会更好。例如，如果训练的时候没有包含测试的词语，那么词类比会产生错误的结果。

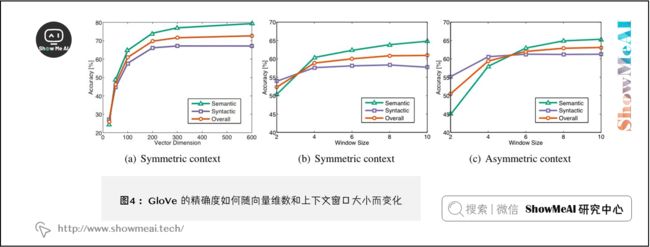
③ 对于极高或者极低维度的词向量，模型的表现较差：

• 低维度的词向量不能捕获在语料库中不同词语的意义。这可以被看作是我们的模型复杂度太低的高偏差问题。例如，我们考虑单词“king”、“queen”、“man”、“woman”。直观上，我们需要使用例如“性别”和“领导”两个维度来将它们编码成2字节的词向量。维度较低的词向量不会捕获四个单词之间的语义差异，而过高的维度的可能捕获语料库中无助于泛化的噪声-即所谓的高方差问题。

❐ 超高维向量：直观地说，这些向量似乎会在语料库中捕获不允许泛化的噪声，即导致高方差。但是Yin等人在On the Dimensionality of Word Embedding上表明，skip-gram和Glove对这种过拟合具有鲁棒性。

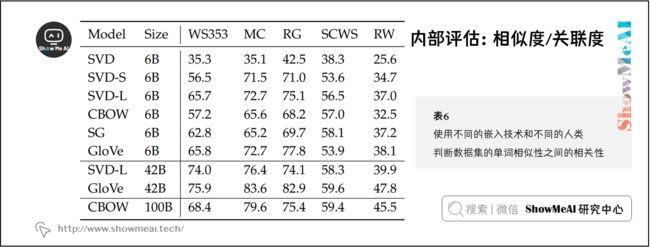
2.5 内部评估示例：相似度/关联度

另外一个评估词向量质量的简单方法是，让人去给两个词的相似度在一个固定的范围内(例如0-10)评分，然后将其与对应词向量的余弦相似度进行对比。这已经在包含人为评估的各种数据集上尝试过。

下图是使用不同的词嵌入技术与不同的人类判断数据集的词向量相似性之间的相关性

2.6 拓展阅读：多义词

我们想知道如何处理在不同的自然语言处理使用场景下，用不同的的词向量来捕获同一个单词在不同场景下的不同用法。例如，“run”是一个名词也是一个动词，在不同的语境中它的词性也会不同。论文 Improving Word Representations Via Global Context And Multiple Word Prototypes 提出上述问题的的解决方法。该方法的本质如下：

• 收集所有出现的单词的固定大小的上下文窗口(例如前5个和后5 个)。
• 每个上下文使用上下文词向量的加权平均值来表示(使用idf加权)。
• 用 spherical k-means 对这些上下文表示进行聚类。
• 最后，每个单词的出现都重新标签为其相关联的类，同时对这个类，来训练对应的词向量。

要对这个问题进行更严谨的处理，可以参考原文。

3.词向量应用于外部任务

到目前为止，我们一直都关注于内在任务，并强调其在开发良好的词向量技术中的重要性。但是大多数实际问题的最终目标是将词向量结果用于其他的外部任务。接下来会讨论处理外部任务的方法。

3.1 外部任务范式

很多 NLP 的外部任务都可以表述为分类任务。例如，给定一个句子，我们可以对这个句子做情感分类，判断其情感类别为正面，负面还是中性。相似地，在命名实体识别(NER)，给定一个上下文和一个中心词，我们想将中心词分类为许多类别之一。对输入，张三在2022年购买了300股腾讯的股票，我们希望有这样的一个分类结果：

$$[张三{]}_{Person}在[2022年{]}_{Time}购买了300股[腾讯{]}_{Organization}的股票$$

对这类问题，我们一般有以下形式的训练集：

$$\{x^{(i)},y^{(i)}{\}}_1^N$$

其中 $x^{(i)}$ 是一个 $d$ 维的词向量， $y^{(i)}$ 是一个 $C$ 维的one-hot向量，表示我们希望最终预测的标签(情感，其他词，专有名词，买／卖决策等)。

我们可以使用诸如逻辑回归和SVM之类的算法对2-D词向量来进行分类，如下图所示

在一般的机器学习任务中，我们通常固定输入数据和目标标签，然后使用优化算法来训练权重(例如梯度下降，L-BFGS，牛顿法等等)。然而在NLP应用中，我们引入一个新的思想：在训练外部任务时对输入字向量进行再训练。下面我们讨论何时使用以及为什么要这样做。

3.2 词向量再训练

在许多情况下，我们会基于内部任务去训练得到词向量，进而再用于外部任务，很多时候这些预训练的词向量在外部评估中表现良好。但是，这些预训练的词向量在外部评估中的表现仍然有提高的可能。当然，重新训练也存在着一定的风险。

如果我们在外部评估中重新训练词向量，这就需要保证训练集足够大并能覆盖词汇表中大部分的单词。这是因为Word2Vec或GloVe会生成语义相关的单词，这些单词位于单词空间的同一部分。

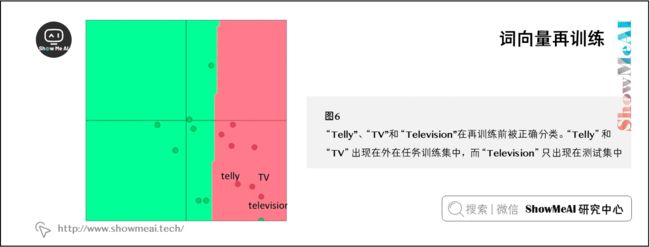
假设预训练向量位于二维空间中，如下图所示。在这里，我们看到在一些外部分类任务中，单词向量被正确分类。

现在，如果我们因为有限的训练集大小而只对其中两个向量进行再训练，那么我们在下图中可以看到，其中一个单词被错误分类了，因为单词向量更新导致边界移动。

因此，如果训练数据集很小，就不应该对单词向量进行再训练。如果训练集很大，再训练可以提高性能。

❐ 实现技巧：对于大型训练数据集，应考虑字向量再训练。对于小数据集，重新训练单词向量可能会降低性能。

3.3 Softmax分类与正则化

我们继续使用Softmax分类函数，其形式如下公式所示：

$$p(y_j=1\mid x)=\frac{exp(W_{j.}x)}{{\sum }_{c=1}^{C}exp(W_{c.}x)}$$

这里我们计算词向量 $x$ 是类别 $j$ 的概率。使用交叉熵损失函数计算一个样本的损失如下所示：

$$-\sum _{j=1}^C{y}_{j}log(p(y_j=1\mid x))=-\sum _{j=1}^C{y}_{j}log\left(\frac{exp(W_{j.}x)}{{\sum }_{c=1}^{C}exp(W_{c.}x)}\right)$$

当然，上述求和是对 $(C-1)$ 个零值求和，因为 $y_j$ 仅在单个索引为1，这意味着 $x$ 仅属于1个正确的类别。现在我们定义 $k$ 为正确类别的索引。因此，我们现在可以简化损失函数：

$$-log\left(\frac{exp(W_{k.}x)}{{\sum }_{c=1}^{C}exp(W_{c.}x)}\right)$$

然后我们可以扩展为有 $N$ 个单词的损失函数：

$$-\sum _{i=1}^{N}log\left(\frac{exp(W_{k(i).}{x}^{(i)})}{{\sum }_{c=1}^{C}exp(W_{c.}{x}^i)}\right)$$

上面公式的唯一不同是 $k(i)$ 现在一个函数，返回 $x^{(i)}$ 对应的每正确的类的索引。

现在我们来估计一下同时训练模型的权值 $(W)$ 和词向量 $(x)$ 时需要更新的参数的数量。我们知道一个简单的线性决策模型至少需要一个 $d$ 维的词向量输入和生成一个 $C$ 个类别的分布。因此更新模型的权值，我们需要 $C\cdot d$ 个参数。如果我们也对词汇表 $V$ 中的每个单词都更新词向量，那么就要更新 $\left|V\right|$ 个词向量，每一个的维度是 $d$ 维。因此对一个简单的线性分类模型，总共的参数数目是 $C\cdot d+\left|V\right|$ ：

$$\begin{array}{r}{\nabla }_{\theta }J(\theta )=\left[\begin{array}{c}{\nabla }_{W_{.1}}\\ ⋮\\ {\nabla }_{W_{.d}}\\ {\nabla }_{aardvark}\\ ⋮\\ {\nabla }_{zebra}\end{array}\right]\end{array}$$

对于一个简单的模型来说，这是相当大的参数量——这样的参数量很可能会出现过拟合的问题。

为了降低过拟合的风险，我们引入一个正则项，从贝叶斯派的思想看，这个正则项是对模型的参数加上一个先验分布，让参数变小(即接近于 $0$ )：

$$-\sum _{i=1}^{N}log\left(\frac{exp(W_{k(i).}{x}^{(i)})}{{\sum }_{c=1}^{C}exp(W_{c.}{x}^i)}\right)+\lambda \sum _{k=1}^{C\cdot d+|V|\cdot d}{\theta }_k^2$$

如果调整好目标权重 $\lambda$ 的值，最小化上面的函数将会降低出现很大的参数值的可能性，同时也提高模型的泛化能力。在我们使用更多参数更复杂的模型(例如神经网络)时，就更加需要正则化的思想。

3.4 窗内容分类

下图是我们有一个中心词和一个长度为2的对称窗口。这样的上下文可以帮助分辨Paris是一个地点还是一个名字。

目前为止，我们主要探讨了使用单个单词向量 $x$ 预测的外部评估任务。在现实中，因为自然语言处理的性质，这几乎不会有这样的任务。在自然语言处理中，常常存在着一词多义的情况，我们一般要利用词的上下文来判断其不同的意义。

例如，如果你要某人解释“to sanction”是什么意思，你会马上意识到根据“to sanction”的上下文其意思可能是“to permit”或者“to punish”。在更多的情况下，我们使用一个单词序列作为模型的输入。这个序列是由中心词向量和上下文词向量组成。上下文中的单词数量也被称为上下文窗口大小，并根据解决的问题而变化。

一般来说，较窄的窗口大小会导致在句法测试中更好的性能，而更宽的窗口会导致在语义测试中更好的性能。

为了将之前讨论的Softmax模型修改为使用单词的窗口来进行分类，我们只需要按照下面形式将 $x^{(i)}$ 替换为 $x_{window}^{(i)}$ ：

$$\begin{array}{r}{x}_{window}^{(i)}=\left[\begin{array}{c}{x}^{(i-2)}\\ x^{(i-1)}\\ x^{(i)}\\ x^{(i+1)}\\ x^{(i+2)}\end{array}\right]\end{array}$$

因此，当我们计算单词的损失梯度如下所示，当然需要分配梯度来更新相应的词向量：

$$\begin{array}{r}{\delta }_{window}=\left[\begin{array}{c}{\nabla }_{x^{(i-2)}}\\ {\nabla }_{x^{(i-1)}}\\ {\nabla }_{x^{(i)}}\\ {\nabla }_{x^{(i+1)}}\\ {\nabla }_{x^{(i+2)}}\end{array}\right]\end{array}$$

当然，梯度将需要分发来更新相应的词向量。

3.5 非线性分类器

我们现在介绍非线性分类模型，如神经网络。我们看到即使是最优的线性分类平面，也有许多样例都被错误的分类。这是因为线性模型在这个数据集上的分类能力有限。

在下图中，我们看到非线性分类模型可以对上面的数据集的样例有着更好的分类结果，这个简答的例子可以初步的说明我们为什么需要非线性模型。

4.拓展阅读

4.1 Improving Distributional Similarity with Lessons Learned from Word Embeddings

实际应用中如何获得更好的词向量

1) Abstract

近年来的研究趋势表明，基于神经网络的词嵌入模型在词相似性和相似性检测任务上优于传统的基于计数的分布模型。我们发现，词嵌入的性能提高在很大程度上是由于某些系统设计选择和超参数优化，而不是嵌入算法本身。此外，我们证明这些修改可以转移到传统的分配模型，产生类似的收益。与以前的报告相比，我们观察到的方法之间的性能差异主要是局部的或不显著的，没有任何一种方法比其他方法具有全局优势。

2) Introduction

然而，最先进的嵌入方法都是基于相同的 bag-of-contexts 的单词。此外，分析表明，word2vec的 SGNS 隐含地分解了单词上下文的PMI矩阵。也就是说，其数学目标和可用的信息来源实际上与传统方法所使用的非常相似。那么其优势来源于什么呢？

虽然模型和优化的目标函数是主要因素，但是其他因素也会影响结果

• 超参数优化：负采样的样本个数，平滑的负采样分布，动态大小的上下文窗口

在这项工作中，我们将这些超参数显式化，并展示了如何将它们应用到传统的基于计数器的方法中。为了评估每个超参数对算法性能的影响，我们进行了实验，比较了四种不同的表示方法，同时控制了不同的超参数

3) Practical Recommendations

通常建议为手头的任务调优所有超参数，以及特定于算法的超参数。然而，这可能是计算昂贵的。因此我们提供一些“经验法则”，我们发现它们在我们的设置中工作得很好：

• 始终使用上下文分布平滑( $cds=0.75$ )来修改PMI，并且适用于 PPMI、SVD 和 SGNS，不断提高性能

不要使用 SVD “correctly” (eig = 1) 。使用对称变体之一

SGNS是健壮的基线。虽然它可能不是每个任务的最佳方法，但它在任何情况下都不会表现得很差。此外，SGNS是最快的训练方法，而且在磁盘空间和内存消耗方面(到目前为止)也是最便宜的。

SGNS适合更多的负样本

对于SGNS和GloVe而言，值得对 $w+c$ 做实验，因为这是容易应用(不需要重新训练)并且带来可观收益(以及可观损失)的。

4) Conclusion

最近的嵌入方法引入了大量的网络结构以外的设计选择和优化算法。我们揭示了这些看似微小的变化对单词表示方法的成功有很大的影响。通过展示如何在传统方法中适应和调整这些超参数，我们对表示进行适当的比较，并从词嵌入文献中挑战各种优势。

本研究还揭示了对更多控制变量实验的需要，并将“变量”的概念从明显的任务、数据和方法扩展到经常忽略的预处理步骤和超参数设置。我们还强调了需要进行透明和可重复的实验，并赞扬诸如Mikolov、Pennington等作者，以及其他人公开提供他们的代码。本着这种精神，我们也公布我们的代码

4.2 Evaluation methods for unsupervised word embeddings

1) Abstract

我们介绍了一种无监督嵌入技术的评估方法，该方法可以从文本中获取有意义的表示。嵌入方法的顺序不同，评价结果也不同，这就对通常认为只有一个最优向量表示的假设提出了质疑。我们提供了一种新的评估技术，可以直接通过特定查询比较词嵌入。这些方法减少了偏差，提供了更大的洞察力，并允许我们通过众包快速准确地征求数据驱动的相关性判断。

2) Discussion

超参数优化会导致明显的性能差异。

实际上，不同的算法编码的信息出奇地不同，这些信息可能与我们想要的用例一致，也可能与我们想要的用例不一致。例如，我们发现词嵌入将关于词频的信息的编码程度不同，即使在长度归一化后也是如此。

这个结果令人惊讶

• 首先，许多算法保留了不同的拦截参数来吸收基于频率的效果。
• 其次，我们希望嵌入空间的几何形状主要由语义驱动：频率相对较小的词应该均匀地分布在空间中，而大量罕见的、特定的单词应该围绕相关但更频繁的单词聚集。

我们训练了一个逻辑回归模型来预测基于词向量的词频类别。训练线性分类器将单词分类为常见或罕见类别，阈值从100到50000不等。在每个阈值频率下，我们对训练集进行采样以确保标签分布在所有频率上的一致性平衡。我们使用了长度归一化的嵌入，因为罕见的单词在训练期间更新较少，可能具有更短的向量(Turian et al.， 2010)。在下图中，我们报告了在每个阈值频率下使用五倍交叉验证的平均准确度和标准偏差( $1\sigma$ )。

所有单词嵌入都比随机的好，这表明它们包含一些频率信息。GloVe和TSCCA在接近1000的词频上达到近100%的准确性。与其他所有嵌入不同，C&W嵌入的更大的词频的准确性增加了。进一步的调查显示，权重矩阵的方向是随词频阈值改变的，这表明词频似乎在嵌入空间中以平滑的方式被编码。

虽然GloVe和CBOW是内在任务上最佳的两种嵌入，但它们在其编码的频率信息量上有很大的差异。因此，我们可以断定，不同的频率预测并不是因为自然语言的内在性质：并不是说频繁的单词自然只有频繁的邻居。

嵌入空间中的词频信息也会影响词的相似性。对于WordSim-353数据集，我们查询了k = 1000 个最近邻居。然后，我们查询其在训练集语料库中频率的排名，平均了所有的查询词。在我们的实验中，我们发现一个单词的频率和它在最近邻中的排名位置有很强的相关性。下图显示了C&W词嵌入中一个词的最近邻排名(关于一次查询)和其词频在训练集语料库中的排名之间的幂律关系 (nn-rank ∼ 1000 · ${\text{corpus-rank}}^{0.17}$ )。这是一个值得关注的问题：语言中单词的频率在人类的文字处理过程中也起着至关重要的作用(Cattell， 1886)。因此，在实验设计中，我们需要明确地把词频作为一个因素来考虑。同时，上述结果也表明，常用的余弦相似度在嵌入空间内的固有任务时，会受到频率效应的影响。我们认为，进一步的研究应该解决如何更好地衡量词与嵌入空间之间的语言关系的问题，例如通过学习自定义度量。

3) Related Work

Mikolov et al. (2013b) 说明嵌入空间存在特定的语言规律。通过在嵌入空间中进行简单的向量运算，可以解决各种句法和语义类比问题。这与之前的工作不同，之前的工作将类比任务描述为一个分类问题(Turney， 2008)。令人惊讶的是，词嵌入似乎捕捉到了更复杂的语言特性。Chen等人(2013)的研究表明，单词嵌入甚至包含了区域拼写(英式与美式)、名词性别和情感极性等信息。

以往的词嵌入评价工作可分为内部评价和外部评价。内在评价通过直接测量语义关联和几何关联之间的相关性来衡量词向量的质量，通常通过查询术语的的库存来实现。Baroni等人(2014)以内在度量为重点，在各种查询清单和任务上比较词嵌入和分布词向量。Faruqui and Dyer (2014)提供了一个网站，该网站允许对一些查询清单的嵌入进行自动评估。Gaoetal.(2014)发表了一份改进的类比推理任务查询清单。最后，Tsvetkov等人(2015)提出了一种新的内在度量方法，该方法可以更好地关联外部效果。然而，所有这些评估都是在预先收集的清单上进行的，并且大多局限于本地指标，如相关性。

外部评估使用嵌入作为其他任务模型中的特征，例如语义角色标记或词性标记(Collobert etal.， 2011)，并提高现有系统的性能(Turianetal.，2010)。然而，他们在其他任务上，如解析，则不太成功(Andreas和Klein， 2014)。

在主题模型的上下文中，无监督语义建模方面做了更多的工作。一个例子是单词入侵任务(Chang et al.， 2009)，其中注释器被要求识别插入到给定主题的一组高概率单词中的随机单词。词嵌入不产生可解释的维度，因此我们不能直接使用这个方法，但是我们提出了一个基于最近邻居的相关任务。手工评估是昂贵和耗时的，但其他研究表明，自动化评估可以紧密地模拟人类的直觉(Newman et al.， 2010)。

4) Conclusion

影响嵌入质量的因素很多。标准的综合评价虽然有用，但不能提供完整或一致的情况。词汇频率等因素在其中扮演着重要的角色，而这在以前是不为人知的。词频也会干扰常用的余弦相似性度量。我们提出了一个新的评估框架，该框架基于嵌入之间的直接比较，为这些嵌入提供了更精细的分析，并支持简单的众包相关性判断。我们还提出了一个新的一致性任务，它测量了我们的直觉，即嵌入空间中的邻域应该在语义或语法上相关。我们发现，外部评估虽然有助于突出嵌入性能的特定方面，但不应该用作通用质量的代理。

5.参考资料

• 《ShowMeAI 深度学习与自然语言处理教程》的PDF在线阅读版本 - note2
• 《斯坦福CS224n深度学习与自然语言处理》课程学习指南
• 《斯坦福CS224n深度学习与自然语言处理》课程大作业解析
• 【双语字幕视频】斯坦福CS224n | 深度学习与自然语言处理(2019·全20讲)
• Stanford官网 | CS224n: Natural Language Processing with Deep Learning

ShowMeAI 深度学习与自然语言处理教程（完整版）

• ShowMeAI 深度学习与自然语言处理教程(1) - 词向量、SVD分解与Word2vec
• ShowMeAI 深度学习与自然语言处理教程(2) - GloVe及词向量的训练与评估
• ShowMeAI 深度学习与自然语言处理教程(3) - 神经网络与反向传播
• ShowMeAI 深度学习与自然语言处理教程(4) - 句法分析与依存解析
• ShowMeAI 深度学习与自然语言处理教程(5) - 语言模型、RNN、GRU与LSTM
• ShowMeAI 深度学习与自然语言处理教程(6) - 神经机器翻译、seq2seq与注意力机制
• ShowMeAI 深度学习与自然语言处理教程(7) - 问答系统
• ShowMeAI 深度学习与自然语言处理教程(8) - NLP中的卷积神经网络
• ShowMeAI 深度学习与自然语言处理教程(9) - 句法分析与树形递归神经网络

ShowMeAI 斯坦福NLP名课 CS224n带学详解（20讲·完整版）

• 斯坦福NLP名课带学详解 | CS224n 第1讲 - NLP介绍与词向量初步
• 斯坦福NLP名课带学详解 | CS224n 第2讲 - 词向量进阶
• 斯坦福NLP名课带学详解 | CS224n 第3讲 - 神经网络知识回顾
• 斯坦福NLP名课带学详解 | CS224n 第4讲 - 神经网络反向传播与计算图
• 斯坦福NLP名课带学详解 | CS224n 第5讲 - 句法分析与依存解析
• 斯坦福NLP名课带学详解 | CS224n 第6讲 - 循环神经网络与语言模型
• 斯坦福NLP名课带学详解 | CS224n 第7讲 - 梯度消失问题与RNN变种
• 斯坦福NLP名课带学详解 | CS224n 第8讲 - 机器翻译、seq2seq与注意力机制
• 斯坦福NLP名课带学详解 | CS224n 第9讲 - cs224n课程大项目实用技巧与经验
• 斯坦福NLP名课带学详解 | CS224n 第10讲 - NLP中的问答系统
• 斯坦福NLP名课带学详解 | CS224n 第11讲 - NLP中的卷积神经网络
• 斯坦福NLP名课带学详解 | CS224n 第12讲 - 子词模型
• 斯坦福NLP名课带学详解 | CS224n 第13讲 - 基于上下文的表征与NLP预训练模型
• 斯坦福NLP名课带学详解 | CS224n 第14讲 - Transformers自注意力与生成模型
• 斯坦福NLP名课带学详解 | CS224n 第15讲 - NLP文本生成任务
• 斯坦福NLP名课带学详解 | CS224n 第16讲 - 指代消解问题与神经网络方法
• 斯坦福NLP名课带学详解 | CS224n 第17讲 - 多任务学习(以问答系统为例)
• 斯坦福NLP名课带学详解 | CS224n 第18讲 - 句法分析与树形递归神经网络
• 斯坦福NLP名课带学详解 | CS224n 第19讲 - AI安全偏见与公平
• 斯坦福NLP名课带学详解 | CS224n 第20讲 - NLP与深度学习的未来

ShowMeAI系列教程精选推荐

• 大厂技术实现：推荐与广告计算解决方案
• 大厂技术实现：计算机视觉解决方案
• 大厂技术实现：自然语言处理行业解决方案
• 图解Python编程：从入门到精通系列教程
• 图解数据分析：从入门到精通系列教程
• 图解AI数学基础：从入门到精通系列教程
• 图解大数据技术：从入门到精通系列教程
• 图解机器学习算法：从入门到精通系列教程
• 机器学习实战：手把手教你玩转机器学习系列
• 深度学习教程：吴恩达专项课程 · 全套笔记解读
• 自然语言处理教程：斯坦福CS224n课程 · 课程带学与全套笔记解读
• 深度学习与计算机视觉教程：斯坦福CS231n · 全套笔记解读