2015 UESTC Winter Training #4【Regionals 2008 :: Asia - Tehran】
2015 UESTC Winter Training #4
Regionals 2008 :: Asia - Tehran
比赛开始时电脑死活也连不上WIFI,导致花了近1个小时才解决_(:зゝ∠)_
未完成:B E F G H I
A - String LD
给n(<=100)个互不相同的字符串(最长为100),然后进行stringld操作,就是每次操作把各个字符串的首个字符删去,直到
- 有字符串完全删去
- 存在两个字符串完全一致
问在最后一次操作之前有几次操作(PS:问法是在太奇怪了,不就是答案减一嘛)
【简单字符串处理】
三层for循环,第一层枚举操作次数,第二层对每个字符串删去首字符,第三层比较,因为比较用了strcmp,相当于多了一层,结果o(n^4)的复杂度,怎么想都要超时啊。现在想想,第三层和第四层并不是全部枚举的,大概只枚举了一半,即最终复杂度是100*100*50*50=25,000,000。仍然很高,但是确实是3ms通过。
B - Painting
n*m(均小于等于100)的棋盘,小明(姑且认为是小明吧)用不同颜色凃这个棋盘,每次涂色将一整行或者一整列涂成一个颜色,给出棋盘的颜色(全都涂上颜色,用不超过10000的数字表示),问涂色的顺序(如果有多个答案,要求输出是字典序最小的)
【拓扑排序】【未完成】
假若某一行是653426,即某一个数出现了两次,那么一定有一次这一行刷的时是6,并且在这之后竖着刷了有5,3,4,2这四种颜色。那么构图从结点6向结点5,3,4,2分别一条有向边,这样构成图。最后做一次拓扑排序即可。
因为数字是10000以内,而结点数最多只有200个(横着刷或者竖着刷最多刷200次),因此做一个映射,把编号映射到1到200间。还因为要字典序最小,所以做映射之前记得要排一下序。
这道题最坑爹的一点据说是可能出现相同的涂色,即两次涂色用的是同一个颜色,因此我目前还没有改对。(因为题目中说了每次使用不同的颜色涂色,因此这个传言是错误的)
有时间再改一下吧。
C - Another Brick in the Wall
给出大小为m*n(均小于等于100)的一面墙,墙上有砖(废话),每块砖高度是一格,输入数据中用数字表示,数字为砖的长度,比如33322,就是一块长为3的砖和一块长为2的砖组合在一起。输入中的0表示这里没有砖。
现在要抽出一块砖。如果抽出砖之后,墙上某一块砖每一部分的下方均空着,那么这块砖就掉落到地上。问最多有多少长度的砖掉下去了(掉下去的包括抽出的砖的长度)。
【记忆化搜索】
这道坑爹的题目整整花了我两个小时的时间,一开始想用动态规划,就是从上到下进行动态规划,每扫描到一块砖,首先将这块砖的长度加进这块砖的dp值中,如果它下方的某块砖抽走后它能跌落,那么就累加入下方的砖的dp值中。
写了一半发现,例外情况
144441
333333
666666
就是说6抽去后,上一层同时跌落两块长度为3的砖,但是当仅有某一块长为3的砖跌落时,再上边长度是4的砖是不会跌落的,也就是说,仅仅是一个砖掉落的状态,传递给下方的砖是不可行的。也就是说需要记录多个砖同时掉落的状态。
那好吧,重新设定dp[f][l][r]是第f层,左边到l,右边到r的最大跌落长度。
但是写了1个小时就写不下去了,实在太麻烦了。
最后想到使用记忆化搜索,记忆化搜索的话可以少算一些不必要的状态。(我真是太机智了,哈哈),仍然使用dp[f][l][r]记录状态,dp[f][l][r]是第f层,左边到l,右边到r的最大跌落长度。每次记忆化搜索,仍然是检查是否存在状态,如果这块砖左边有x个空位,右边有y个空位,就把[l,r]延伸至[l-x,r+y],总之是等价的。
接着就是检查上方是否有砖跌落,如果上方没有砖(也就是在第一行),就把l~r的砖的长度输出(注意可能有空位,也就是说扫描一遍计算长度),如果有砖,判断上方能跌落砖的区间,加上dp[f-1][ll][rr](ll,rr为所判断出来的区间)即可,进行递归搜索。
判断跌落区间的话我是预处理了一下,使用p[i][j]存放
D - Blast the Enemy!
给出一个多边形,n(边数小于100)个点的坐标(绝对值小于100,是整数),求重心
题目很良心地给了矢量公式:其中COM(C)表示图形C的重心坐标
【计算几何】
题目很良心地给了计算公式

公式变形一下
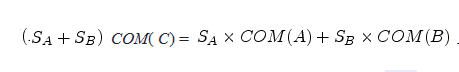
也就是将多边形分成几个n-2三角形,对每个三角形分别求重心(三个坐标加起来除以3)和面积(叉积)
最后再除以三角形面积总和即可。
因为叉积分为正负,之间可以抵消,所以可以不必考虑三角形的选取问题。
I - Fruit Weights
还没有看这道题,据说
像这种大于小于的关系,使用差分约束系统比较合适