数值分析-函数逼近计算
数值分析-函数逼近计算
- 前言
- 敲黑板
- 函数的最佳平方逼近
- 正交多项式
- 其他常见的正交多项式
-
- Legendre(勒让德)多项式
- Chebyshev(切比雪夫)多项式
- 函数按正交多项式展开
- 正交函数作最小二乘拟合
-
- 代码实现
- Test example
- 最佳一致逼近
-
- 基础内容
- 如何得到OUAP
- 代码实现
- 未完待续
前言
上一篇在多项式插值中我们介绍了几种经典方法,如Lagrange、Neville、Newton、逐次线性和Hermite插值等。多项式插值虽然可以在插值节点处一定经过给定的函数值,但是在插值节点之外的误差无法保证,经常出现剧烈震荡的情况。本章函数逼近计算的主要目的是在某种误差度量下求得最佳的逼近函数。多项式插值可以当作是一种局部准确拟合,函数逼近更多的是要求整体的拟合误差要小。
具体内容详见 《数值分析》 李庆扬、王能超、易大义(华中科大出版社)第三章
敲黑板
-
函数逼近其实很常见,在很多科学实验中的最小二乘拟合函数便是一个应用,在之前的矩阵论专题中有稍作讲解,相信大家都有一个目标:数据点都给我划到线上,啊啊啊!!
-
两种误差度量形式:设原函数为 f ( x ) f(x) f(x),x的取值范围为 a < x < b a < x < b a<x<b,逼近函数为 P ( x ) P(x) P(x)
- 一致逼近/均匀逼近: ∣ ∣ f ( x ) − P ( x ) ∣ ∣ ∞ = m a x a < x < b ∣ f ( x ) − P ( x ) ∣ \large ||f(x)-P(x)||_\infty=max_{a < x < b}|f(x)-P(x)| ∣∣f(x)−P(x)∣∣∞=maxa<x<b∣f(x)−P(x)∣
- 均方逼近/平方逼近: ∣ ∣ f ( x ) − P ( x ) ∣ ∣ 2 = ∫ a b [ f ( x ) − P ( x ) ] 2 d x \large ||f(x)-P(x)||_2=\sqrt{\int_a^b[f(x)-P(x)]^2 dx} ∣∣f(x)−P(x)∣∣2=∫ab[f(x)−P(x)]2dx
-
根据教材的内容,我们来引入函数的内积空间及范数定义:
-
函数的内积:设 f ( x ) , g ( x ) , ρ ( x ) ∈ C [ a , b ] f(x),g(x),\rho(x) \in C[a,b] f(x),g(x),ρ(x)∈C[a,b],其中 ρ ( x ) \rho(x) ρ(x)是权函数
权函数的定义为: ∫ a b ∣ x ∣ n ρ ( x ) d x ( n = 0 , 1 , . . , n ) \int_a^b |x|^n \rho(x) dx \,\, (n=0,1,..,n) ∫ab∣x∣nρ(x)dx(n=0,1,..,n)存在,且当 ∫ a b g ( x ) ρ ( x ) d x = 0 \int_a^b g(x) \rho(x) dx=0 ∫abg(x)ρ(x)dx=0时,则 g ( x ) ≡ 0 ∈ [ a , b ] g(x) \equiv 0 \in [a,b] g(x)≡0∈[a,b],其各阶矩也存在
两个函数在区间 [ a , b ] [a,b] [a,b]上的的内积表示为: ( f , g ) = ∫ a b ρ ( x ) f ( x ) g ( x ) d x (f,g)=\int_a^b \rho(x)f(x)g(x) dx (f,g)=∫abρ(x)f(x)g(x)dx
关于向量内积空间的性质同样适用于函数内积空间,如正定性、线性性、交换性
-
函数的Euclid范数: ∣ ∣ f ∣ ∣ 2 = ∫ a b ρ ( x ) f 2 ( x ) d x = ( f , f ) ||f||_2=\sqrt{\int_a^b \rho(x)f^2(x)dx}=\sqrt{(f,f)} ∣∣f∣∣2=∫abρ(x)f2(x)dx=(f,f)
关于向量范数的不等式同样适用于函数范数,如柯西不等式、三角不等式、平行四边形定律。
-
函数线性无关性:设 ϕ 0 ( x ) , ϕ 1 ( x ) , . . . , ϕ n − 1 ( x ) ∈ C [ a , b ] \phi_0(x),\phi_1(x),...,\phi_{n-1}(x) \in C[a,b] ϕ0(x),ϕ1(x),...,ϕn−1(x)∈C[a,b],如果有
a 0 ϕ ( x ) + a 1 ϕ 1 ( x ) + . . . + a n − 1 ϕ n − 1 ( x ) = 0 a_0 \phi_(x)+a_1 \phi_1(x)+...+a_{n-1}\phi_{n-1}(x)=0 a0ϕ(x)+a1ϕ1(x)+...+an−1ϕn−1(x)=0,当且仅当 a 0 = a 1 = . . . = a n − 1 = 0 a_0=a_1=...=a_{n-1}=0 a0=a1=...=an−1=0时成立,则称 ϕ 0 ( x ) , ϕ 1 ( x ) , . . . , ϕ n − 1 ( x ) \phi_0(x),\phi_1(x),...,\phi_{n-1}(x) ϕ0(x),ϕ1(x),...,ϕn−1(x)在区间 [ a , b ] [a,b] [a,b]上是线性无关的。
给出判断函数线性相关性质的定理: ϕ 0 ( x ) , ϕ 1 ( x ) , . . . , ϕ n − 1 ( x ) \phi_0(x),\phi_1(x),...,\phi_{n-1}(x) ϕ0(x),ϕ1(x),...,ϕn−1(x)在区间 [ a , b ] [a,b] [a,b]上线性无关的充要条件是其克莱姆矩阵行列式不为0,即
G n − 1 = G ( ϕ 0 ( x ) , ϕ 1 ( x ) , . . . , ϕ n − 1 ( x ) ) = ∣ ( ϕ 0 , ϕ 0 ) ( ϕ 0 , ϕ 1 ) . . . ( ϕ 0 , ϕ n − 1 ) ( ϕ 1 , ϕ 0 ) ( ϕ 1 , ϕ 1 ) . . . ( ϕ 1 , ϕ n − 1 ) ⋮ ⋮ ⋱ ⋮ ( ϕ n − 1 , ϕ 0 ) ( ϕ n − 1 , ϕ 1 ) . . . ( ϕ n − 1 , ϕ n − 1 ) ∣ (1) G_{n-1}=G(\phi_0(x),\phi_1(x),...,\phi_{n-1}(x))=\left | \begin{matrix} (\phi_0,\phi_0) & (\phi_0,\phi_1) & ... & (\phi_0,\phi_{n-1})\\ (\phi_1,\phi_0) & (\phi_1,\phi_1) & ... & (\phi_1,\phi_{n-1})\\ \vdots & \vdots & \ddots& \vdots \\ (\phi_{n-1},\phi_0) & (\phi_{n-1},\phi_1) & ... & (\phi_{n-1},\phi_{n-1}) \end{matrix} \right | \tag{1} Gn−1=G(ϕ0(x),ϕ1(x),...,ϕn−1(x))=∣∣∣∣∣∣∣∣∣(ϕ0,ϕ0)(ϕ1,ϕ0)⋮(ϕn−1,ϕ0)(ϕ0,ϕ1)(ϕ1,ϕ1)⋮(ϕn−1,ϕ1)......⋱...(ϕ0,ϕn−1)(ϕ1,ϕn−1)⋮(ϕn−1,ϕn−1)∣∣∣∣∣∣∣∣∣(1)
- 这里试着证明其充分性,采用反证法,即若 G n − 1 = 0 G_{n-1}=0 Gn−1=0,可以推得 ϕ 0 ( x ) , ϕ 1 ( x ) , . . . , ϕ n − 1 ( x ) \phi_0(x),\phi_1(x),...,\phi_{n-1}(x) ϕ0(x),ϕ1(x),...,ϕn−1(x)在区间 [ a , b ] [a,b] [a,b]上线性相关:
令
A = [ ( ϕ 0 , ϕ 0 ) ( ϕ 0 , ϕ 1 ) . . . ( ϕ 0 , ϕ n − 1 ) ( ϕ 1 , ϕ 0 ) ( ϕ 1 , ϕ 1 ) . . . ( ϕ 1 , ϕ n − 1 ) ⋮ ⋮ ⋱ ⋮ ( ϕ n − 1 , ϕ 0 ) ( ϕ n − 1 , ϕ 1 ) . . . ( ϕ n − 1 , ϕ n − 1 ) ] (2) A=\left [ \begin{matrix} (\phi_0,\phi_0) & (\phi_0,\phi_1) & ... & (\phi_0,\phi_{n-1})\\ (\phi_1,\phi_0) & (\phi_1,\phi_1) & ... & (\phi_1,\phi_{n-1})\\ \vdots & \vdots & \ddots& \vdots \\ (\phi_{n-1},\phi_0) & (\phi_{n-1},\phi_1) & ... & (\phi_{n-1},\phi_{n-1}) \end{matrix} \right ] \tag{2} A=⎣⎢⎢⎢⎡(ϕ0,ϕ0)(ϕ1,ϕ0)⋮(ϕn−1,ϕ0)(ϕ0,ϕ1)(ϕ1,ϕ1)⋮(ϕn−1,ϕ1)......⋱...(ϕ0,ϕn−1)(ϕ1,ϕn−1)⋮(ϕn−1,ϕn−1)⎦⎥⎥⎥⎤(2)
由于 G n − 1 = 0 G_{n-1}=0 Gn−1=0,则 A β = 0 A\beta =0 Aβ=0有有非零解, β ≠ 0 \beta \neq 0 β=0,对于第k行,
( ϕ k , ϕ 0 ) β 0 + ( ϕ k , ϕ 1 ) β 1 + . . . + ( ϕ k , ϕ n − 1 ) β n − 1 = 0 (\phi_k,\phi_0)\beta_0+(\phi_k,\phi_1)\beta_1+...+(\phi_k,\phi_{n-1})\beta_{n-1}=0 (ϕk,ϕ0)β0+(ϕk,ϕ1)β1+...+(ϕk,ϕn−1)βn−1=0
即 ( ϕ k , ∑ i = 0 n − 1 β i ϕ i ) = 0 , ( k = 0 , 1 , . . . , n − 1 ) (\phi_k,\sum_{i=0}^{n-1}\beta_i \phi_i)=0, (k=0,1,...,n-1) (ϕk,∑i=0n−1βiϕi)=0,(k=0,1,...,n−1)
记 Φ = ∑ i = 0 n − 1 β i ϕ i \Phi=\sum_{i=0}^{n-1}\beta_i \phi_i Φ=∑i=0n−1βiϕi,我们可以得到
( Φ , Φ ) = ( Φ , ∑ i = 0 n − 1 β i ϕ i ) = ∑ i = 0 n − 1 β i ( Φ , ϕ i ) = 0 (\Phi,\Phi)=(\Phi,\sum_{i=0}^{n-1}\beta_i \phi_i)=\sum_{i=0}^{n-1}\beta_i(\Phi,\phi_i)=0 (Φ,Φ)=(Φ,i=0∑n−1βiϕi)=i=0∑n−1βi(Φ,ϕi)=0
根据函数内积的正定性,可以得到 Φ = 0 \Phi=0 Φ=0,即 ∑ i = 0 n − 1 β i ϕ i = 0 , β ≠ 0 \sum_{i=0}^{n-1}\beta_i \phi_i=0, \beta \neq0 ∑i=0n−1βiϕi=0,β=0,得 ϕ j \phi_j ϕj线性相关,证毕。必要性一样可以用反证法证得!
若函数系 ϕ i {\phi_i} ϕi线性相关,则存在不全为0的数 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an使得:
∑ i = 0 n − 1 a i ϕ i = 0 \sum_{i=0}^{n-1}a_i \phi_i = 0 i=0∑n−1aiϕi=0
等式两边同乘 ϕ 1 , ϕ 2 , . . . , ϕ n − 1 \phi_1,\phi_2,...,\phi_n-1 ϕ1,ϕ2,...,ϕn−1,便得到方程组: ∑ i = 0 n − 1 ∑ j = 0 n − 1 a i ( ϕ i , ϕ j ) = 0 \sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_i (\phi_i,\phi_j) = 0 i=0∑n−1j=0∑n−1ai(ϕi,ϕj)=0
因其有非零解,所以系数矩阵的行列式一定为0,与 G n − 1 ≠ 0 G_{n-1} \neq 0 Gn−1=0矛盾,得证。
- 这里试着证明其充分性,采用反证法,即若 G n − 1 = 0 G_{n-1}=0 Gn−1=0,可以推得 ϕ 0 ( x ) , ϕ 1 ( x ) , . . . , ϕ n − 1 ( x ) \phi_0(x),\phi_1(x),...,\phi_{n-1}(x) ϕ0(x),ϕ1(x),...,ϕn−1(x)在区间 [ a , b ] [a,b] [a,b]上线性相关:
-
函数的最佳平方逼近
-
定义:设 f ( x ) ∈ C [ a , b ] , Φ = s p a n { ϕ 0 , ϕ 1 , . . . , ϕ n } f(x) \in C[a,b], \Phi=span \{ \phi_0,\phi_1,...,\phi_n \} f(x)∈C[a,b],Φ=span{ϕ0,ϕ1,...,ϕn},若存在 S ∗ ( x ) ∈ Φ S^*(x) \in \Phi S∗(x)∈Φ,使得
∣ ∣ f − S ∗ ∣ ∣ 2 2 = m i n S ∈ Φ ∣ ∣ f − S ∣ ∣ 2 2 = m i n S ∈ Φ ∫ b a ρ ( x ) [ f ( x ) − S ( x ) ] 2 d x ||f-S^*||_2^2=min_{S \in \Phi} ||f-S||_2^2=min_{S \in \Phi} \int_b^a\rho(x)[f(x)-S(x)]^2dx ∣∣f−S∗∣∣22=minS∈Φ∣∣f−S∣∣22=minS∈Φ∫baρ(x)[f(x)−S(x)]2dx
称 S ∗ ( x ) S^*(x) S∗(x)是 f ( x ) f(x) f(x)在 Φ ∈ C [ a , b ] \Phi \in C[a,b] Φ∈C[a,b]上的最佳逼近平方函数。
其中, S ∗ ( x ) S^*(x) S∗(x)可以表示成 S ∗ ( x ) = ∑ j = 0 n a j ϕ j ( x ) S^*(x)=\sum_{j=0}^n a_j \phi_j(x) S∗(x)=∑j=0najϕj(x),等价于关于 ( a 0 , a 1 , . . . , a n ) (a_0,a_1,...,a_n) (a0,a1,...,an)函数的最小值:
a r g m i n { I ( a 0 , a 1 , . . . , a n ) } = ∫ a b ρ ( x ) [ ∑ j = 0 n a j ϕ j ( x ) − f ( x ) ] 2 d x argmin\{ I(a_0,a_1,...,a_n) \} =\int_a^b \rho(x)[\sum_{j=0}^n a_j \phi_j(x)-f(x)]^2dx argmin{I(a0,a1,...,an)}=∫abρ(x)[j=0∑najϕj(x)−f(x)]2dx
这是一个多元函数的极值问题,我们先利用其必要条件来试着求解,即在极值点处偏导数为0,
∂ I ∂ a k = 2 ∫ a b ρ ( x ) [ ∑ j = 0 n a j ϕ j ( x ) − f ( x ) ] ϕ k ( x ) d x = 0 , ( k = 0 , 1 , . . . , n ) \frac{\partial I}{\partial a_k}=2\int_a^b \rho(x) [\sum_{j=0}^n a_j \phi_j(x)-f(x)]\phi_k(x)dx=0, (k=0,1,...,n) ∂ak∂I=2∫abρ(x)[j=0∑najϕj(x)−f(x)]ϕk(x)dx=0,(k=0,1,...,n)
可以得到称为法方程的约束方程:
∑ j = 0 n a j ( ϕ k , ϕ j ) = ( f , ϕ k ) , ( k = 0 , 1 , . . . , n ) \large \sum_{j=0}^n a_j (\phi_k,\phi_j)=(f,\phi_k) , (k=0,1,...,n) j=0∑naj(ϕk,ϕj)=(f,ϕk),(k=0,1,...,n)
由于 ϕ j \phi_j ϕj线性无关, G n ( ϕ 0 , ϕ 1 , . . . , ϕ n ) ≠ 0 G_n(\phi_0,\phi_1,...,\phi_n) \neq0 Gn(ϕ0,ϕ1,...,ϕn)=0,所以法方程有唯一解 a k ∗ a^*_k ak∗,接下来证明所求解 S ∗ ( x ) = a 0 ∗ ϕ 0 ( x ) + a 1 ∗ ϕ 1 ( x ) + . . . + a n ∗ ϕ n ( x ) S^*(x)=a_0^* \phi_0(x)+a_1^* \phi_1(x)+...+a_n^*\phi_n(x) S∗(x)=a0∗ϕ0(x)+a1∗ϕ1(x)+...+an∗ϕn(x)为令 I I I为最小值的解:
即证明: ∫ b a ρ ( x ) [ f ( x ) − S ∗ ( x ) ] 2 d x ≤ ∫ b a ρ ( x ) [ f ( x ) − S ( x ) ] 2 d x \int_b^a\rho(x)[f(x)-S^*(x)]^2dx \leq \int_b^a\rho(x)[f(x)-S(x)]^2dx ∫baρ(x)[f(x)−S∗(x)]2dx≤∫baρ(x)[f(x)−S(x)]2dx
D = ∫ b a ρ ( x ) [ f ( x ) − S ( x ) ] 2 d x − ∫ b a ρ ( x ) [ f ( x ) − S ∗ ( x ) ] 2 d x (3) D=\int_b^a\rho(x)[f(x)-S(x)]^2dx-\int_b^a\rho(x)[f(x)-S^*(x)]^2dx \tag{3} D=∫baρ(x)[f(x)−S(x)]2dx−∫baρ(x)[f(x)−S∗(x)]2dx(3)
这里我们需要用到 S ∗ ( x ) S^*(x) S∗(x)为解的性质,即
∑ j = 0 n a j ∗ ( ϕ k , ϕ j ) = ( f , ϕ k ) , ( k = 0 , 1 , . . . , n ) → ( f − ∑ j = 0 n ϕ j a j ∗ , ϕ k ) = 0 → ( f − S ∗ ( x ) , ϕ k ) = 0 , ( k = 0 , 1 , . . . , n ) \sum_{j=0}^n a^*_j (\phi_k,\phi_j)=(f,\phi_k) , (k=0,1,...,n) \rightarrow \,\, (f-\sum_{j=0}^n \phi_j a^*_j, \phi_k)=0 \rightarrow \,\, (f-S^*(x),\phi_k)=0, (k=0,1,...,n) j=0∑naj∗(ϕk,ϕj)=(f,ϕk),(k=0,1,...,n)→(f−j=0∑nϕjaj∗,ϕk)=0→(f−S∗(x),ϕk)=0,(k=0,1,...,n)
所以我们要凑出 ( f − S ∗ ( x ) , ϕ k ) (f-S^*(x),\phi_k) (f−S∗(x),ϕk)这一项,这一步稍显复杂,可以将式3化成下面的形式:
D = ∫ b a ρ ( x ) [ S ( x ) − S ∗ ( x ) ] 2 d x − 2 ∫ b a ρ ( x ) [ S ∗ ( x ) − S ( x ) ] [ f ( x ) − S ∗ ( x ) ] d x (4) D=\int_b^a\rho(x)[S(x)-S^* (x)]^2dx-2\int_b^a\rho(x)[S^*(x)-S(x)][f(x)-S^*(x)]dx \tag{4} D=∫baρ(x)[S(x)−S∗(x)]2dx−2∫baρ(x)[S∗(x)−S(x)][f(x)−S∗(x)]dx(4)
而 S ∗ ( x ) − S ( x ) S^*(x)-S(x) S∗(x)−S(x)可以用 ( ϕ 0 , ϕ 1 , . . . , ϕ n ) (\phi_0,\phi_1,...,\phi_n) (ϕ0,ϕ1,...,ϕn)线性表出,所以式4中第二项积分为0,即有
D = ∫ b a ρ ( x ) [ S ( x ) − S ∗ ( x ) ] 2 d x ≥ 0 (5) D=\int_b^a\rho(x)[S(x)-S^* (x)]^2dx \geq 0 \tag{5} D=∫baρ(x)[S(x)−S∗(x)]2dx≥0(5)
即证明所求解 S ∗ ( x ) = a 0 ∗ ϕ 0 ( x ) + a 1 ∗ ϕ 1 ( x ) + . . . + a n ∗ ϕ n ( x ) S^*(x)=a_0^* \phi_0(x)+a_1^* \phi_1(x)+...+a_n^*\phi_n(x) S∗(x)=a0∗ϕ0(x)+a1∗ϕ1(x)+...+an∗ϕn(x)为令 I I I为最小值的解
-
逼近误差
令逼近误差 δ = f − S ∗ ( x ) \delta=f-S^*(x) δ=f−S∗(x),其平方误差为:
∣ ∣ δ ∣ ∣ 2 2 = ( f − S ∗ , f − S ∗ ) = ( f , f − S ∗ ) − ( S ∗ , f − S ∗ ) = ( f , f ) − ( f , S ∗ ) = ∣ ∣ f ∣ ∣ 2 2 − ∑ k = 0 n a k ∗ ( f , ϕ k ) (6) ||\delta||_2^2=(f-S^*,f-S^*) = (f,f-S^*)-(S^*,f-S^*)=(f,f)-(f,S^*)=||f||_2^2-\sum_{k=0}^n a_k^* (f,\phi_k) \tag{6} ∣∣δ∣∣22=(f−S∗,f−S∗)=(f,f−S∗)−(S∗,f−S∗)=(f,f)−(f,S∗)=∣∣f∣∣22−k=0∑nak∗(f,ϕk)(6)
可以发现式6的第二项即法方程的右边项。
正交多项式
-
在求解最佳平方逼近时要法方程,为一个n阶线性方程组,由上可知,法方程存在唯一非零解,但是当n达到一定程度时,法方程的系数矩阵,即
G n − 1 = G ( ϕ 0 ( x ) , ϕ 1 ( x ) , . . . , ϕ n − 1 ( x ) ) = ∣ ( ϕ 0 , ϕ 0 ) ( ϕ 0 , ϕ 1 ) . . . ( ϕ 0 , ϕ n − 1 ) ( ϕ 1 , ϕ 0 ) ( ϕ 1 , ϕ 1 ) . . . ( ϕ 1 , ϕ n − 1 ) ⋮ ⋮ ⋱ ⋮ ( ϕ n − 1 , ϕ 0 ) ( ϕ n − 1 , ϕ 1 ) . . . ( ϕ n − 1 , ϕ n − 1 ) ∣ G_{n-1}=G(\phi_0(x),\phi_1(x),...,\phi_{n-1}(x))=\left | \begin{matrix} (\phi_0,\phi_0) & (\phi_0,\phi_1) & ... & (\phi_0,\phi_{n-1})\\ (\phi_1,\phi_0) & (\phi_1,\phi_1) & ... & (\phi_1,\phi_{n-1})\\ \vdots & \vdots & \ddots& \vdots \\ (\phi_{n-1},\phi_0) & (\phi_{n-1},\phi_1) & ... & (\phi_{n-1},\phi_{n-1}) \end{matrix} \right | Gn−1=G(ϕ0(x),ϕ1(x),...,ϕn−1(x))=∣∣∣∣∣∣∣∣∣(ϕ0,ϕ0)(ϕ1,ϕ0)⋮(ϕn−1,ϕ0)(ϕ0,ϕ1)(ϕ1,ϕ1)⋮(ϕn−1,ϕ1)......⋱...(ϕ0,ϕn−1)(ϕ1,ϕn−1)⋮(ϕn−1,ϕn−1)∣∣∣∣∣∣∣∣∣
会是一个病态矩阵,求解结果受计算机舍入误差影响会剧烈抖动。
这里如果当 G n G_n Gn为一个对角矩阵时,求解是十分简单直接的,不会存在抖动问题,这就要求 ϕ k \phi_k ϕk之间是互相正交的,即
( ϕ i , ϕ k ) = 0 i f i ! = k e l s e 1 (\phi_i,\phi_k)=0 \,\, if \,\, i!=k \,\, else \,\, 1 (ϕi,ϕk)=0ifi!=kelse1
同一线性空间的两组基是可以互相转换的,而将一组基转化为正交基有多种方法,最常见的便是施密特正交化,这在线代部分有介绍过给大家。
其实很常见的一个多项式函数正交基就是 1 , x , x 2 , . . . , x n {1,x,x^2,...,x^n} 1,x,x2,...,xn,利用施密特正交化给出的正交多项式 g n ( x ) g_n(x) gn(x)有以下性质:
- g n ( x ) g_n(x) gn(x)是最高项系数为1的n次多项式
- 任一n次多项式 P n ( x ) ∈ H n P_n(x) \in H_n Pn(x)∈Hn均可表示为 g 0 ( x ) , g 1 ( x ) , . . . , g n ( x ) g_0(x),g_1(x),...,g_n(x) g0(x),g1(x),...,gn(x)的线性组合
- g n ( x ) g_n(x) gn(x)与任一次数小于n的多项式正交:很好理解, g n ( x ) g_n(x) gn(x)是 H n H_n Hn的一组基,则任何次数小于n的多项式都可以由 g 0 , g 1 , . . . , g n − 1 g_0,g_1,...,g_{n-1} g0,g1,...,gn−1线性组成,则必与 g n ( x ) g_n(x) gn(x)正交
- 存在 g n − 1 ( x ) g_{n-1}(x) gn−1(x)、 g n ( x ) g_n(x) gn(x)和 g n + 1 ( x ) g_{n+1}(x) gn+1(x)的递推式:
g n + 1 ( x ) = ( x − α n ) g n ( x ) − β n g n − 1 ( x ) , n = 0 , 1 , . . . , g 0 ( x ) = 1 , g − 1 ( x ) = 0 , α n = ( x g n , g n ) ( g n , g n ) β n = ( g n , g n ) ( g n − 1 , g n − 1 ) \begin{aligned} &g_{n+1}(x) =(x-\alpha_n)g_n(x)-\beta_ng_{n-1}(x), n=0,1,...,\\ &g_0(x)=1,g_{-1}(x)=0,\\ &\alpha_n=\frac{(xg_n,g_n)}{(g_n,g_n)}\\ &\beta_n=\frac{(g_n,g_n)}{(g_{n-1},g_{n-1})} \end{aligned} gn+1(x)=(x−αn)gn(x)−βngn−1(x),n=0,1,...,g0(x)=1,g−1(x)=0,αn=(gn,gn)(xgn,gn)βn=(gn−1,gn−1)(gn,gn)
- 设 g 0 ( x ) , g 1 ( x ) , . . . , g n ( x ) g_0(x),g_1(x),...,g_n(x) g0(x),g1(x),...,gn(x)是在区间 [ a , b ] [a,b] [a,b]上带权函数 ρ ( x ) \rho(x) ρ(x)的正交多项式,则 g n ( x ) g_n(x) gn(x)的n个根都是单重实根,且都在区间 [ a , b ] [a,b] [a,b]
其他常见的正交多项式
Legendre(勒让德)多项式
-
区间为 [ − 1 , 1 ] [-1,1] [−1,1],权函数为1,其形式如下:
P 0 ( x ) = 1 , P n ( x ) = 1 2 n n ! d n d x n { ( x 2 − 1 ) n } \large P_0(x)=1,P_n(x)=\frac{1}{2^n n!}\frac{d^n}{dx^n}\{ (x^2-1)^n \} P0(x)=1,Pn(x)=2nn!1dxndn{(x2−1)n}
∫ − 1 1 P n ( x ) P m ( x ) d x = 2 2 n + 1 i f n ≠ m e l s e 0 \int_{-1}^{1} P_n(x)P_m(x)dx=\frac{2}{2n+1} \,\, if \,\, n \neq m \,\, else\,\,0 ∫−11Pn(x)Pm(x)dx=2n+12ifn=melse0
其中 ( x 2 − 1 ) n (x^2-1)^n (x2−1)n是2n次多项式,则求导n次后,最高项系数为:
a n = ( 2 n ) ! 2 n ( n ! ) 2 \large a_n=\frac{(2n)!}{2^n (n!)^2} an=2n(n!)2(2n)!
若将最高项系数归化为1,则归一化后的勒让德多项式形式为:
P n ( x ) ‾ = n ! 2 n ! d n d x n { ( x 2 − 1 ) n } \large \overline{P_n(x)} =\frac{n!}{2n!}\frac{d^n}{dx^n}\{ (x^2-1)^n \} Pn(x)=2n!n!dxndn{(x2−1)n}
-
递推公式
( n + 1 ) P n + 1 ( x ) = ( 2 n + 1 ) x P n ( x ) − n P n − 1 ( x ) , P 0 ( x ) = 1 , P 1 ( x ) = x \large (n+1)P_{n+1}(x)=(2n+1)xP_n(x)-nP_{n-1}(x),P_0(x)=1,P_1(x)=x (n+1)Pn+1(x)=(2n+1)xPn(x)−nPn−1(x),P0(x)=1,P1(x)=x
Chebyshev(切比雪夫)多项式
-
区间为 [ − 1 , 1 ] [-1,1] [−1,1],权函数为 ρ ( x ) = 1 1 − x 2 \rho(x)=\frac{1}{\sqrt{1-x^2}} ρ(x)=1−x21,其形式如下:
T n ( x ) = c o s ( n arccos x ) , ∣ x ∣ ≤ 1 T_n(x)=cos(n \arccos{x}), |x| \leq 1 Tn(x)=cos(narccosx),∣x∣≤1
如果令 x = c o s θ x=cos \theta x=cosθ,则可以写成:
T n ( x ) = cos n θ , 0 ≤ θ ≤ π T_n(x)=\cos{n\theta}, 0 \leq \theta \leq \pi Tn(x)=cosnθ,0≤θ≤π
-
递推公式:
T n + 1 ( x ) = 2 x T n ( x ) − T n − 1 ( x ) , T 0 ( x ) = 1 , T 1 ( x ) = x \large T_{n+1}(x)=2xT_n(x)-T_{n-1}(x),T_0(x)=1,T_1(x)=x Tn+1(x)=2xTn(x)−Tn−1(x),T0(x)=1,T1(x)=x
由递推式我们可以知道,切比雪夫多项式的首项系数为 2 n − 1 2^{n-1} 2n−1,且偶次项只有偶次幂,奇次项只有奇次幂。
函数按正交多项式展开
-
Q: 若 f ( x ) ∈ C [ a , b ] f(x) \in C[a,b] f(x)∈C[a,b],用正交多项式 { g 0 , g 1 , . . . , g n } \{g_0,g_1,...,g_n\} {g0,g1,...,gn}作基,求最佳平方逼近多项式
S n ( x ) = a 0 g 0 ( x ) + a 1 g 1 ( x ) + . . . + a n g n ( x ) S_n(x)=a_0g_0(x)+a_1g_1(x)+...+a_ng_n(x) Sn(x)=a0g0(x)+a1g1(x)+...+angn(x)
在前面最佳平方逼近内容中,我们得到法方程如下:
∑ j = 0 n a j ( ϕ k , ϕ j ) = ( f , ϕ k ) , ( k = 0 , 1 , . . . , n ) \large \sum_{j=0}^n a_j (\phi_k,\phi_j)=(f,\phi_k) , (k=0,1,...,n) j=0∑naj(ϕk,ϕj)=(f,ϕk),(k=0,1,...,n)
由于 { g 0 , g 1 , . . . , g n } \{g_0,g_1,...,g_n\} {g0,g1,...,gn}是正交多项式,可得
a k = ( f , g k ) ( g k , g k ) , ( k = 0 , 1 , . . . , n ) (6) \large a_k=\frac{(f,g_k)}{(g_k,g_k)} , (k=0,1,...,n) \tag{6} ak=(gk,gk)(f,gk),(k=0,1,...,n)(6)
所以函数在正交多项式下的最佳平方逼近为:
f → S n ( x ) = ∑ k = 0 n ( f , g k ) ( g k , g k ) g k ( x ) \large f \rightarrow S_n(x)=\sum_{k=0}^n \frac{(f,g_k)}{(g_k,g_k)} g_k(x) f→Sn(x)=k=0∑n(gk,gk)(f,gk)gk(x)
注意使用勒让德或者切比雪夫多项式逼近函数时要在定义域 [ − 1 , 1 ] [-1,1] [−1,1]内,如果不在此范围,需要用线性变换使x的范围落在 [ − 1 , 1 ] [-1,1] [−1,1]内。
若 x ∈ [ a , b ] x \in [a,b] x∈[a,b],则令 x = b − a 2 t + b + a 2 , − 1 ≤ t ≤ 1 \large x=\frac{b-a}{2}t+\frac{b+a}{2}, -1 \leq t \leq 1 x=2b−at+2b+a,−1≤t≤1,即 F ( t ) = f ( b − a 2 t + b + a 2 ) F(t)=f(\frac{b-a}{2}t+\frac{b+a}{2}) F(t)=f(2b−at+2b+a),求得对应的最佳平方逼近函数 S ∗ ( x ) S^*(x) S∗(x)后, f ( x ) f(x) f(x)对应的最佳平方逼近函数即为 S ∗ ( 1 b − a ( 2 x − a − b ) ) S^*(\frac{1}{b-a}(2x-a-b)) S∗(b−a1(2x−a−b))
正交函数作最小二乘拟合
-
给出对应的点集 { x i } , { y i } \{ x_i \}, \{y_i \} {xi},{yi},取带权函数 ω ( x ) \omega(x) ω(x)的正交函数集为 { ϕ 0 , ϕ 1 , . . . , ϕ n } \{ \phi_0,\phi_1,...,\phi_n \} {ϕ0,ϕ1,...,ϕn},注意这里的点是离散的,而我们到上面为止所提到的内积都是基于函数定积分,离散的正交拟合在计算机上实现上更便捷。
-
由式6可知,离散形式的各正交基系数为:
a k ∗ = ( f , ϕ k ) ( ϕ k , ϕ k ) = ∑ i = 0 m ω ( x i ) f ( x i ) ϕ k ( x i ) ∑ i = 0 m ω ( x i ) ϕ k 2 ( x i ) , ( k = 0 , 1 , . . . , n ) \large a_k^*=\frac{(f,\phi_k)}{(\phi_k,\phi_k)}=\frac{\sum_{i=0}^m \omega(x_i)f(x_i)\phi_k(x_i)}{\sum_{i=0}^m \omega(x_i) \phi_k^2(x_i)},(k=0,1,...,n) ak∗=(ϕk,ϕk)(f,ϕk)=∑i=0mω(xi)ϕk2(xi)∑i=0mω(xi)f(xi)ϕk(xi),(k=0,1,...,n)
其实正交多项式最小二乘拟合与常见的最小二乘拟合(在之前矩阵论中我们曾介绍过)很类似,但要注意区间范围和权函数等。理论上正交多项式所构成的系数矩阵避免了病态问题,求解是更加高效的。
代码实现
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
class Orthogonal_Polynomials_Fitting:
""" Fitting points by Orthogonal polynomials
Author: Junno
Date: 2022-03-24
"""
def __init__(self, x, y):
"""__init__
Args:
x ([np.array]): [x of points]
y ([np.array]): [y of points]
"""
assert x.shape[0] == y.shape[0] or len(x) == len(y)
self.x = x
self.y = y
self.N = self.x.shape[0]
self.LP_records = {}
self.CH_records = {}
self.low = np.min(x)
self.high = np.max(x)
self.shift = False
# if x's range not in [-1,1], do linear shift
if self.low < -1 or self.high > 1:
self.shift = True
self.shift_x = np.arange(-1, 1, 2./self.N)
@classmethod
# recursion formula of Legender Polynomials
def Legender_Polynomials(self, x, n):
if n == 0:
return 1
elif n == 1:
return x
else:
if (x, n) in self.LP_records.keys():
return self.LP_records[(x, n)]
else:
ans = ((2*n-1)*x*Legender_Polynomials(x, n-1) -
(n-1)*Legender_Polynomials(x, n-2))/(n)
self.LP_records[(x, n)] = ans
return ans
@classmethod
# recursion formula of Chebyshev Polynomials
def Chebyshev_Polynomials(self, x, n):
if n == 0:
return 1
else:
# let x=cos(theta), 0<=theta<=pi, Tn(x)=cos(n*theta)
return np.cos(n*x)
# elif n==1:
# return x
# else:
# if (x,n) in self.CH_records.keys():
# return self.CH_records[(x,n)]
# else:
# ans=2*x*Chebyshev_Polynomials(x,n-1)-Chebyshev_Polynomials(x,n-2)
# self.CH_records[(x,n)]=ans
# return ans
def calculate(self, order, method='Legender', show_error=True, show_fitting_result=True):
"""calculate_I calculate y for order and method
Args:
order ([int], optional): [interpolation order]. Defaults to 1.
show_error (bool, optional): [print fitting error]. Defaults to True.
show_fitting_result (bool, optional): [show fitting result by plt]. Defaults to True.
Returns:
[predict y]: [as show]
"""
cx = self.shift_x if self.shift else self.x
if method == 'Legender':
Method = Legender_Polynomials
elif method == 'Chebyshev':
Method = Chebyshev_Polynomials
# with x=cosθ,we can let the weight function to be 1
cx = np.arange(0, np.pi, np.pi/cx.shape[0])
A = np.zeros((order, order))
for i in range(order):
for x_ in cx:
A[i, i] += Method(x_, i)*Method(x_, i)
B = np.zeros((order, 1))
for i in range(order):
for x_, y_ in zip(cx, self.y):
B[i, 0] += Method(x_, i)*y_
# solute coefficients
ai = np.linalg.inv(A)@B
predict_y = np.zeros_like(self.y)
for j in range(order):
for i in range(cx.shape[0]):
# x_ = self.x[i] if not self.shift else 1/(self.high-self.low)*(2*self.x[i]-self.high-self.low)
predict_y[i] += Method(cx[i], j)*ai[j, 0]
error=np.linalg.norm(y-predict_y)
if show_error:
print("Fitting Error: {:.5f}".format(error))
if show_fitting_result:
plt.subplot(111)
plt.scatter(self.x, self.y, s=5, marker='*', c='green')
plt.scatter(self.x, predict_y, s=5, marker='o', c='red')
Raw = mpatches.Patch(color='green', label='Raw Points')
Predict = mpatches.Patch(color='red', label='Predict Points')
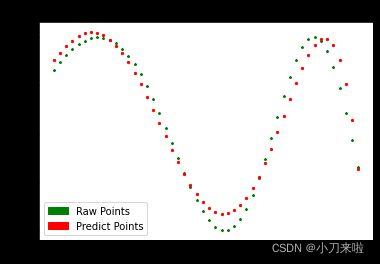
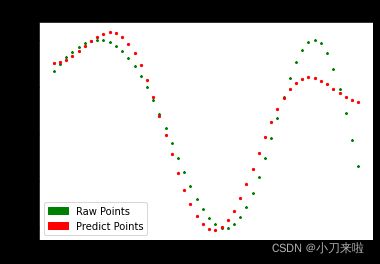
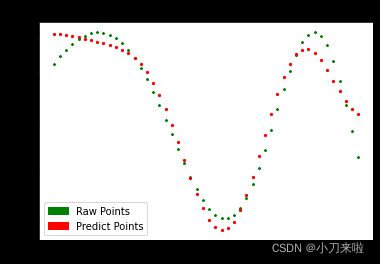
plt.title('Orthogonal-Polynomials by {} with {} orders'.format(method,order))
plt.legend(handles=[Raw, Predict], loc='best')
plt.show()
return predict_y,error
Test example
# prepare some point set
F=lambda x: np.cos(2*np.exp(x))
x=np.arange(1,2,0.02)
y=F(x)
OP=Orthogonal_Polynomials_Fitting(x,y)
# Legender Method
py, _=OP.calculate(5,method='Legender')
>>> Fitting Error: 1.50786
py, _=OP.calculate(6,method='Legender')
>>> Fitting Error: 0.91998
# Chebyshev Method
py, _=OP.calculate(5,method='Chebyshev')
>>> Fitting Error: 1.45608
py, _=OP.calculate(6,method='Chebyshev')
>>> Fitting Error: 1.02585
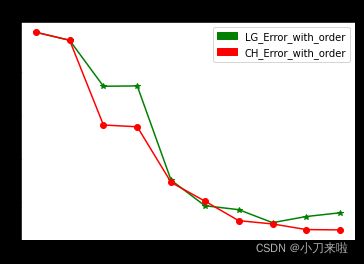
# show error with order and methods
LG_Error_with_order=[]
CH_Error_with_order=[]
for i in range(1,11):
py,error=OP.calculate(i,method='Legender',show_error=False,show_fitting_result=False)
LG_Error_with_order.append(error)
py,error=OP.calculate(i,method='Chebyshev',show_error=False,show_fitting_result=False)
CH_Error_with_order.append(error)
plt.subplot(111)
plt.plot(np.arange(0,10,1),LG_Error_with_order, marker='*',c='green')
plt.plot(np.arange(0,10,1),CH_Error_with_order,marker='o',c='red')
LG_Error=mpatches.Patch(color='green', label='LG_Error_with_order')
CH_Error=mpatches.Patch(color='red', label='CH_Error_with_order')
plt.title('Errors with different Orthogonal-Polynomials and Orders')
plt.legend(handles=[LG_Error,CH_Error],loc='best')
plt.show()
最佳一致逼近
基础内容
-
前面我们提到一致逼近或者说均匀逼近的误差衡量形式为: ∣ ∣ f ( x ) − P ( x ) ∣ ∣ ∞ = m a x a < x < b ∣ f ( x ) − P ( x ) ∣ ||f(x)-P(x)||_\infty=max_{a < x < b}|f(x)-P(x)| ∣∣f(x)−P(x)∣∣∞=maxa<x<b∣f(x)−P(x)∣,一般我们做函数逼近时比较喜欢用均方逼近,即最小二乘的误差衡量,因为平方的引入使得误差函数容易求导,而最佳一致逼近则是一种基于绝对值的最小最大问题,不易求导,研究起来稍微会困难一些。但是,没有跨不过的困难,只有勇敢的Chebyshev!
-
最佳一致逼近多项式OUAP(optimal uniform approximating polynomial)
设 f ∈ C [ a , b ] , p n ∈ H n = s p a n { 1 , x , . . . , x n } f \in C[a,b], p_n \in H_n=span\{ 1,x,...,x^n \} f∈C[a,b],pn∈Hn=span{1,x,...,xn},记 Δ ( f , p n ) = ∣ ∣ f − p n ∣ ∣ ∞ = m a x a ≤ x ≤ b ∣ f ( x ) − p n ( x ) ∣ \Delta (f,p_n)=|| f-p_n||_{\infty}=max_{a \leq x \leq b} |f(x)-p_n(x)| Δ(f,pn)=∣∣f−pn∣∣∞=maxa≤x≤b∣f(x)−pn(x)∣为 p n p_n pn与 f f f的偏差。由定义知, Δ ( f , p n ) ≥ 0 \Delta (f,p_n) \geq 0 Δ(f,pn)≥0。
若 x 0 x_0 x0满足 p ( x 0 ) − f ( x 0 ) = ± ∣ ∣ P − f ∣ ∣ ∞ p(x_0)-f(x_0)=\pm ||P-f||_{\infty} p(x0)−f(x0)=±∣∣P−f∣∣∞,称 x 0 x_0 x0为正or负偏差点。
在 H n H_n Hn中,如果存在满足, E n = i n f p n ∈ H n Δ ( f , p n ) = m i n p n ∈ H n Δ ( f , p n ) = m i n p n ∈ H n [ m a x a ≤ x ≤ b ∣ f ( x ) − p n ( x ) ∣ ] E_n=inf_{p_n \in H_n} \Delta (f,p_n)=min_{p_n \in H_n} \Delta (f,p_n)=min_{p_n \in H_n} [max_{a \leq x \leq b} |f(x)-p_n(x)|] En=infpn∈HnΔ(f,pn)=minpn∈HnΔ(f,pn)=minpn∈Hn[maxa≤x≤b∣f(x)−pn(x)∣],称 E n E_n En为 p n p_n pn与 f f f的最小偏差,满足上式的 p n p_n pn称为 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上的最佳一致逼近多项式。
-
若 P ( x ) ∈ H n P(x) \in H_n P(x)∈Hn是OUAP,则同时存在正负偏差点
证明如下:采用反证法,设只有正偏差点
对于所有 x ∈ [ a , b ] x \in [a,b] x∈[a,b],都有 P ( x ) − f ( x ) > − E n P(x)-f(x) > -E_n P(x)−f(x)>−En,因 P ( x ) − f ( x ) P(x)-f(x) P(x)−f(x)在 [ a , b ] [a,b] [a,b]连续,故最小值大于 − E n -E_n −En,记为 − E n + 2 h , h > 0 -E_n+2h, h>0 −En+2h,h>0,即有:
− E n + 2 h ≤ P ( x ) − f ( x ) ≤ E n -E_n+2h \leq P(x)-f(x) \leq E_n −En+2h≤P(x)−f(x)≤En
− E n + h ≤ [ P ( x ) − h ] − f ( x ) ≤ E n − h -E_n+h \leq [P(x)-h]-f(x) \leq E_n-h −En+h≤[P(x)−h]−f(x)≤En−h
∣ [ P ( x ) − h ] − f ( x ) ∣ ≤ E n − h |[P(x)-h]-f(x) | \leq E_n-h ∣[P(x)−h]−f(x)∣≤En−h
则可得 P ( x ) − h P(x)-h P(x)−h与 f ( x ) f(x) f(x)的偏差小于 E n E_n En,与给定条件矛盾,得证OUAP同时存在正负偏差点。
-
OUAP的充分必要条件(Chebyshev 最佳一致逼近定理)
P ( x ) ∈ H n P(x) \in H_n P(x)∈Hn是 f ( x ) ∈ C [ a , b ] f(x) \in C[a,b] f(x)∈C[a,b]的最佳一致逼近多项式的充要条件为 P ( x ) P(x) P(x)在 [ a , b ] [a,b] [a,b]上至少有n+2个轮流的正负偏差点,即有n+2个点 a ≤ x 1 < x 2 < . . . < x n + 2 ≤ b a \leq x_1 < x_2 < ... < x_{n+2} \leq b a≤x1<x2<...<xn+2≤b,使得
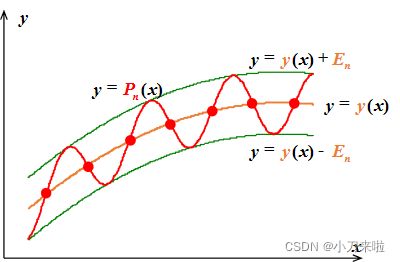
P ( x k ) − f ( x k ) = ( − 1 ) k σ ∣ ∣ P ( x ) − f ( x ) ∣ ∣ ∞ , σ = ± 1 , k = 1 , 2 , . . . , n + 2 P(x_k)-f(x_k)=(-1)^k \sigma ||P(x)-f(x)||_{\infty}, \sigma=\pm1, k=1,2,...,n+2 P(xk)−f(xk)=(−1)kσ∣∣P(x)−f(x)∣∣∞,σ=±1,k=1,2,...,n+2图示如下:
-
OUAP的存在性与唯一性
-
存在性证明:Borel定理,证明复杂从略
-
唯一性证明:
采用反证法证明,设存在两个最佳一致逼近多项式 P ( x ) P(x) P(x)和 Q ( x ) Q(x) Q(x),则对于 x ∈ [ a , b ] x \in [a,b] x∈[a,b],都有:
− E n ≤ P ( x ) − f ( x ) ≤ E n -E_n \leq P(x)-f(x) \leq E_n −En≤P(x)−f(x)≤En, − E n ≤ Q ( x ) − f ( x ) ≤ E n -E_n \leq Q(x)-f(x) \leq E_n −En≤Q(x)−f(x)≤En
可以简单验证得到对于P和Q的加权和为1的线性组合都是 H n H_n Hn的OUAP。
将上面两个式子各以 1 / 2 1/2 1/2加权然后相加,得:
− E n ≤ P ( x ) + Q ( x ) 2 − f ( x ) ≤ E n -E_n \leq \frac{P(x)+Q(x)}{2}-f(x) \leq E_n −En≤2P(x)+Q(x)−f(x)≤En
则 R ( x ) = P ( x ) + Q ( x ) 2 R(x)=\frac{P(x)+Q(x)}{2} R(x)=2P(x)+Q(x)也是OUAP,有 n + 2 n+2 n+2个交错点 { x k } \{ x_k \} {xk}满足 R ( x k ) − f ( x k ) = ( − 1 ) k σ E n , ( k = 1 , 2 , . . . , n + 2 ) R(x_k)-f(x_k)=(-1)^k \sigma E_n,(k=1,2,...,n+2) R(xk)−f(xk)=(−1)kσEn,(k=1,2,...,n+2)
由偏差点的定义,可得:
E n = ∣ R ( x k ) − f ( x k ) ∣ = ∣ P ( x k ) − f ( x k ) 2 + Q ( x k ) − f ( x k ) 2 ∣ (7) \large E_n=|R(x_k)-f(x_k)|=|\frac{P_(x_k)-f(x_k)}{2}+\frac{Q_(x_k)-f(x_k)}{2}|\tag{7} En=∣R(xk)−f(xk)∣=∣2P(xk)−f(xk)+2Q(xk)−f(xk)∣(7)
由于 ∣ P ( x k ) − f ( x k ) ∣ ≤ E n , ∣ Q ( x k ) − f ( x k ) ∣ ≤ E n |P(x_k)-f(x_k)| \leq E_n, |Q(x_k)-f(x_k)| \leq E_n ∣P(xk)−f(xk)∣≤En,∣Q(xk)−f(xk)∣≤En,当且仅当
P ( x k ) − f ( x k ) 2 = Q ( x k ) − f ( x k ) 2 = ± E n 2 \frac{P_(x_k)-f(x_k)}{2}=\frac{Q_(x_k)-f(x_k)}{2}=\pm \frac{E_n}{2} 2P(xk)−f(xk)=2Q(xk)−f(xk)=±2En
时式7成立,即有 P ( x k ) − f ( x k ) = Q ( x k ) − f ( x k ) P_(x_k)-f(x_k)=Q_(x_k)-f(x_k) P(xk)−f(xk)=Q(xk)−f(xk),得 P ( x k ) = Q ( x k ) P(x_k)=Q(x_k) P(xk)=Q(xk)。说明 P ( x ) − Q ( x ) ∈ H n P(x)-Q(x) \in H_n P(x)−Q(x)∈Hn有n+2个零点,只能得到 P ( x ) − Q ( x ) = 0 P(x)-Q(x) =0 P(x)−Q(x)=0,即 P ( x ) = Q ( x ) P(x)=Q(x) P(x)=Q(x),与条件设定矛盾,证得OUAP是唯一的。
-
如何得到OUAP
-
从上面的内容我们可以得到,OUAP有n+2个正负交错点,即有n+1个根,所以 P n ( x ) P_n(x) Pn(x)可以看成是 f ( x ) f(x) f(x)的一个n阶插值多项式。 以Lagrange插值法为例,那我们接下来的问题就是确定这n+1个插值节点的位置,使得得到的插值函数正好是 f ( x ) f(x) f(x)的OUAP。
-
根据OUAP的条件和Lagrange的误差余项,满足OUAP的插值多项式即为其对应的误差余项的无穷范数最小,即
∣ ∣ R n ( x ) ∣ ∣ ∞ = ∣ ∣ f n + 1 ( ξ ) ( n + 1 ) ! ∏ i = 0 n ( x − x i ) ∣ ∣ ∞ ||R_n(x)||_{\infty}=||\frac{f^{n+1}(\xi)}{(n+1)!} \prod_{i=0}^n (x-x_i)||_{\infty} ∣∣Rn(x)∣∣∞=∣∣(n+1)!fn+1(ξ)i=0∏n(x−xi)∣∣∞
其中,假设 f n + 1 ( ξ ) f^{n+1}(\xi) fn+1(ξ)连续且有上限,则我们要求 { x 1 , . . , x n } \{x_1, .., x_n \} {x1,..,xn}使得 w n ( x ) = ∏ i = 0 n ( x − x i ) w_n(x)=\prod_{i=0}^n (x-x_i) wn(x)=∏i=0n(x−xi)形式下的 ∣ ∣ w n ( x ) ∣ ∣ ∞ ||w_n(x)||_{\infty} ∣∣wn(x)∣∣∞最小。(注意,这里我们的约束条件是 w n ( x ) w_n(x) wn(x)的上界最小,一不定就是最小的 w ( x ) w(x) w(x),所以这是一个近似求解)
假设 w n ( x ) w_n(x) wn(x)是最高项系数为1的n阶多项式,可以表示为 w n ( x ) = x n − P n − 1 ( x ) w_n(x)=x^n-P_{n-1}(x) wn(x)=xn−Pn−1(x),则问题转变为求 x n x^n xn的n-1阶OUAP。
这里求得 x n x^n xn的n-1阶OUAP不是通过直接求解,前面定理说明OUAP是存在且唯一的,即只要我们找到一个满足条件的OUAP(存在n+1个交错正负偏差点),那就可以解决问题。
-
(虽然感觉很突兀,但老师也是这么说的)考虑 [ − 1 , 1 ] [-1,1] [−1,1]上Chebyshev多项式, T n ( x ) = cos ( n arccos ( x ) ) T_n(x)=\cos (n \arccos(x)) Tn(x)=cos(narccos(x)),在 x k = cos ( k n π ) , ( k = 0 , 1 , . . . , n ) x_k=\cos(\frac{k}{n} \pi),(k=0,1,...,n) xk=cos(nkπ),(k=0,1,...,n)时, T n ( x ) T_n(x) Tn(x)交错取得极大值1和极小值-1;当 x k = cos ( 2 k − 1 2 n π ) , ( k = 1 , . . . , n ) x_k=\cos(\frac{2k-1}{2n} \pi),(k=1,...,n) xk=cos(2n2k−1π),(k=1,...,n)时, T n ( x ) = 0 T_n(x)=0 Tn(x)=0,即有n个零点。
可以令归一化的Chebyshev多项式(最高项系数为1)为 1 2 n − 1 T n ( x ) = x n − P n − 1 ∗ ( x ) \frac{1}{2^{n-1}}T_n(x)=x^n-P^*_{n-1}(x) 2n−11Tn(x)=xn−Pn−1∗(x),即其无穷范数可以表示为
∣ ∣ 1 2 n − 1 T n ( x ) ∣ ∣ ∞ = 1 2 n − 1 ∣ ∣ T n ( x ) ∣ ∣ ∞ = 1 2 n − 1 ||\frac{1}{2^{n-1}}T_n(x)||_{\infty}=\frac{1}{2^{n-1}}||T_n(x)||_{\infty}=\frac{1}{2^{n-1}} ∣∣2n−11Tn(x)∣∣∞=2n−11∣∣Tn(x)∣∣∞=2n−11 -
结论
即在 [ − 1 , 1 ] [-1,1] [−1,1]上求使得 w n ( x ) = ∏ i = 0 n ( x − x i ) w_n(x)=\prod_{i=0}^n (x-x_i) wn(x)=∏i=0n(x−xi)的无穷范数最小的形式即为归一化的Chebyshev多项式,要求的插值节点即为 T n ( x ) T_n(x) Tn(x)的n+1个零点。
对于一般区间的 x ∈ [ a , b ] x \in [a,b] x∈[a,b],可作变量替换 x = a + b 2 + b − 1 2 t x=\frac{a+b}{2}+\frac{b-1}{2}t x=2a+b+2b−1t,则 t ∈ [ − 1 , 1 ] t \in [-1,1] t∈[−1,1],此时有:
w n + 1 ( x ) = w n + 1 ( a + b 2 + b − a 2 t ) = ( a + b 2 + b − 1 2 t − x 0 ) . . . ( a + b 2 + b − 1 2 t − x n ) = ( b − a 2 ) n + 1 ( t − t 0 ) . . . ( t − t n ) = ( b − a 2 ) n + 1 1 2 n T n + 1 ( t ) w_{n+1}(x)=w_{n+1}(\frac{a+b}{2}+\frac{b-a}{2}t)=(\frac{a+b}{2}+\frac{b-1}{2}t-x_0)...(\frac{a+b}{2}+\frac{b-1}{2}t-x_n)=(\frac{b-a}{2})^{n+1}(t-t_0)...(t-t_n)=(\frac{b-a}{2})^{n+1}\frac{1}{2^{n}}T_{n+1}(t) wn+1(x)=wn+1(2a+b+2b−at)=(2a+b+2b−1t−x0)...(2a+b+2b−1t−xn)=(2b−a)n+1(t−t0)...(t−tn)=(2b−a)n+12n1Tn+1(t)
即以 x k = a + b 2 + b − a 2 cos ( 2 k + 1 2 n + 2 ) π x_k=\frac{a+b}{2}+\frac{b-a}{2} \cos(\frac{2k+1}{2n+2})\pi xk=2a+b+2b−acos(2n+22k+1)π为插值节点, ( k = 0 , 1 , . . . , n ) (k=0,1,...,n) (k=0,1,...,n)。其余项:
R n ( x ) = f n + 1 ( ξ ) ( n + 1 ) ! ( b − a ) n + 1 2 2 n + 1 T n + 1 ( t ) R_n(x)=\frac{f^{n+1}(\xi)}{(n+1)!}\frac{(b-a)^{n+1}}{2^{2n+1}}T_{n+1}(t) Rn(x)=(n+1)!fn+1(ξ)22n+1(b−a)n+1Tn+1(t)有最小上界。
代码实现
- 以 f ( x ) = e x f(x)=e^x f(x)=ex为例, 若控制误差余项在 0.5 × 1 0 − 4 0.5 \times 10^{-4} 0.5×10−4内,则Chebyshev插值节点的个数n可由 ∣ R n ( x ) ∣ ≤ e ( n + 1 ) ! × 1 2 2 n + 1 < 1 2 × 1 0 − 4 |R_n(x)| \leq \frac{e}{(n+1)!} \times \frac{1}{2^{2n+1}} < \frac{1}{2} \times 10^{-4} ∣Rn(x)∣≤(n+1)!e×22n+11<21×10−4确定,即n=4。下面验证以上过程及最后的误差余项上界是否满足条件:
# https://blog.csdn.net/weixin_40519529/article/details/123215263
import numpy as np
from functools import reduce
import matplotlib.pyplot as plt
# Lagrange 线性插值函数
class Lagrange_Polynomial_Interpolation(object):
"""Lagrange_Polynomial_Interpolation
base function: Ln(x)=\sum_{k=0}^{n} yk l_k(x)
Author: Junno
Date: 2022-03-01
"""
def __init__(self, x, y):
"""__init__
Args:
x ([np.array]): [x of points]
y ([np.array]): [y of points]
"""
self.N = x.shape[0]
self.x = np.copy(x)
self.y = np.copy(y)
def calculate_lk(self, x, k,):
"""calculate_lk(x)
base function: lk(x)=∏——{j=0,j!=k}^{n} (x-xj)/(xk-xj)
Args:
x ([float]): [x]
k ([int]): [k]
Returns:
[float]: [lk(x)]
"""
ta = reduce(lambda x, y: x*y, [x-self.x[i]
for i in range(self.N) if i != k])
tb = reduce(lambda x, y: x*y, [self.x[k]-self.x[i]
for i in range(self.N) if i != k])
return ta/tb
def predict(self, x):
"""predict
Args:
x ([float]): [x]
Returns:
[float]: [predict y]
"""
return np.sum([self.y[k]*self.calculate_lk(x, k) for k in range(self.N)])
# points
x0=0
xn=1
x=np.arange(x0,xn,1/10)
F=lambda x :np.exp(x)
y=F(x)
order=5
Cheby_zero_points=np.array([np.cos(np.pi/(2*order)*(2*i+1)) for i in range(order)])
nx=(x0+xn)/2+(xn-x0)/2*Cheby_zero_points
nx=np.sort(nx)
print(nx)
>>> array([0.02447174, 0.20610737, 0.5 , 0.79389263, 0.97552826])
LP=Lagrange_Polynomial_Interpolation(nx,F(nx))
py=np.array([LP.predict(k) for k in x])
print(np.max(np.abs(py-y)))
>>> 2.885868676028025e-05
未完待续
- 码字不易,给个赞吧~