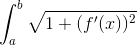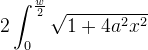LA 3485 (积分 辛普森自适应法) Bridge

桥的间隔数为n = ceil(B/D)，每段绳子的长度为L / n，相邻两塔之间的距离为 B / n

主要问题还是在于已知抛物线的开口宽度w 和 抛物线的高度h 求抛物线的长度

弧长积分公式为：

设抛物线方程为f(x) = ax²，则这段抛物线弧长为

查积分表或者自己分部积分算一下： 

二分抛物线高度x，使得每段抛物线长度为L / n，所求答案为H - x

 1 #include <cstdio>

 2 #include <cmath>

 3 

 4 inline double F(double a, double x)

 5 {//sqrt(a^2+x^2)的原函数

 6     double a2 = a*a, x2 = x*x;

 7     double s = sqrt(a2+x2);

 8     return (x*s + a2*log(x+s))/2;

 9 }

10 

11 double length(double w, double h)

12 {//宽为w，高为h的抛物线的长度

13     double a = 4*h/w/w;

14     double b = 0.5/a;

15     return 4*a*(F(b, w/2) - F(b, 0));

16 }

17 

18 int main()

19 {

20     //freopen("in.txt", "r", stdin);

21 

22     int T;

23     scanf("%d", &T);

24     for(int kase = 1; kase <= T; kase++)

25     {

26         int D, H, B, L;

27         scanf("%d%d%d%d", &D, &H, &B, &L);

28         int n = (B-1)/D + 1;    //间隔数

29         double d = (double)B / n; //间隔

30         double l = (double)L / n;   //每段绳长

31         double Left = 0, Right = H;

32         while(Right - Left > 1e-5)

33         {//二分求抛物线高度

34             double mid = (Right + Left) / 2;

35             if(length(d, mid) > l) Right = mid;

36             else Left = mid;

37         }

38         if(kase > 1) puts("");

39         printf("Case %d:\n%.2f\n", kase, H-Left);

40     }

41 

42     return 0;

43 }

代码君

 

后面又介绍了一种Simpson自适应算法，可以求任意连续函数的积分。

维基百科辛普森法则

虽然不明白这个式子是怎么来的，但并不能阻止我们学习自适应辛普森算法。

书上还说可以将区间端点和中点的函数值作为参数传入以减少重复计算，求教。。

 1 #include <cstdio>

 2 #include <cmath>

 3 

 4 double a;

 5 

 6 inline double F(double x)

 7 { return sqrt(1+4*a*a*x*x); }

 8 

 9 double simpson(double a, double b)

10 {

11     double c = (a+b)/2;

12     return (F(a)+4*F(c)+F(b))*(b-a)/6;

13 }

14 

15 double asr(double a, double b, double eps, double A)

16 {

17     double c = (a+b)/2;

18     double L = simpson(a, c), R = simpson(c, b);

19     if(fabs(L+R-A) <= 15*eps) return L + R + (L+R-A)/15.0;

20     return asr(a, c, eps/2, L) + asr(c, b, eps/2, R);

21 }

22 

23 double asr(double a, double b, double eps)

24 {

25     return asr(a, b, eps, simpson(a, b));

26 }

27 

28 double length(double w, double h)

29 {

30     a = 4.0*h/w/w;

31     return asr(0, w/2, 1e-5) * 2;

32 }

33 

34 int main()

35 {

36     //freopen("in.txt", "r", stdin);

37 

38     int T;

39     scanf("%d", &T);

40     for(int kase = 1; kase <= T; kase++)

41     {

42         int D, H, B, L;

43         scanf("%d%d%d%d", &D, &H, &B, &L);

44         int n = (B-1)/D + 1;

45         double d = (double)B / n;

46         double l = (double)L / n;

47         double x = 0, y = H;

48         while(y - x > 1e-5)

49         {

50             double m = (x + y) / 2;

51             if(length(d, m) > l) y = m;

52             else x = m;

53         }

54         if(kase > 1) puts("");

55         printf("Case %d:\n%.2f\n", kase, H - x);

56     }

57 

58     return 0;

59 }

代码君