数据分析基础教程 （2）

Matplotlib

Matplotlib是Python绘图的始祖。现阶段的大部分高级绘图包如 Seaborn、holoviews、ggplot及 Pandas中的 plot()函数等都是基于 Matplotlib 定制的。换而言之，那些高级绘图包能做到的事，Matplotlib也能做到，只是可能需要长时间的调试及较多的代码才能达到同一目 的，这有点类似于C和Python的关系。

Matplotlib是一个Python 2D绘图库，起初是为了模仿MATLAB中的 绘图命令而开发的，现在可以在各种 Web 应用及像 Jupyter Notebook 这 样的交互式环境中绘画图像。Matplotlib拥有丰富且完善的说明文档， 我们可以仅使用几行代码就生成散点图、直方图、柱形图及饼图等，也 可以使用命令来控制图中的字体、标题、轴等属性。

虽然对于科学家而言，绘图的美观性可能并不重要，只要能清晰地 表达出数据的含义就足够了，然而在金融或者互联网领域，绘图的美观 性就显得尤为重要了，此时如果依旧使用Matplotlib，代码的数量就会 变得愈发冗长。Seaborn就是为了解决这一问题而出现的。

Seaborn

能画出引人注目的图表是非常重要的，例如在探索一个数据集时能 绘制出美观的图表是件令人高兴的事；又如，我们在与观众交流观点 时，也需要让图表吸引观众的注意力并让其印象深刻。Matplotlib 的自 动化程度非常高，掌握如何设置系统以获得一个具有吸引力的图表并不 容易。为了优化 Matplotlib 图表的外观，Seaborn 模块自带许多定制主 题和高级接口。 Seaborn模块被用于在Python中制作有吸引力的统计图形，它构建在 Matplotlib之上，支持NumPy和Pandas的数据结构，以及来自SciPy和 StatsModels的统计结果。该模块旨在用尽可能少的参数生成尽可能漂亮 的图形，不过 Seaborn 是对 Matplotlib 的补充，而不是替代品。 Seaborn的主要功能如下。

1. 通过内置主题改善Matplotlib的外观。
2. 有丰富的调色板工具，可更好地显示数据。
3. 对变量分布进行可视化。
4. 数据矩阵可视化，并使用聚类算法发现这些矩阵中的结构。
5. 对自变量和因变量之间的线性回归结果进行可视化。
6. 绘制统计时间序列，并将其不确定性可视化。
7. 构建高级、抽象的网格图，可轻松地将复杂的问题可视化。

Seaborn 的主题管理

Seaborn的一个重要优点是内置了经过美化的主题，这类似于我们 经常使用的PPT模板，用户无须在外观调整上花费多余的精力。我们通 过一个简单的例子进行理解。

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False  #用来正常显示负号

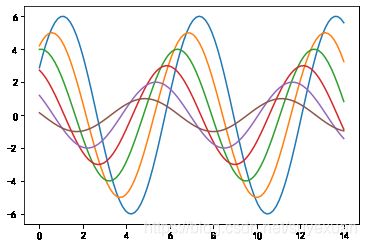
def sinplot(flip=1):
    x = np.linspace(0, 14, 100)
    for i in range(1, 7):
        plt.plot(x, np.sin(x + i * .5) * (7 - i) * flip)
        
sinplot()

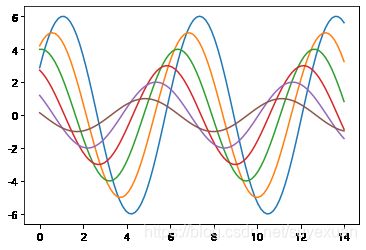
引入Seaborn模块，不经过任何设置，只需简单的import即 可生效。可以看到，背景色变成了浅灰色，还生成了白色网格线，颜色 饱和度也降低了，曲线与背景之间的对比变得不那么强烈，简而言之，看上去很舒服。

import seaborn as sns
sns.set_style({"font.sans-serif":['Microsoft YaHei', 'SimHei']})  #显示中文
        
sinplot()

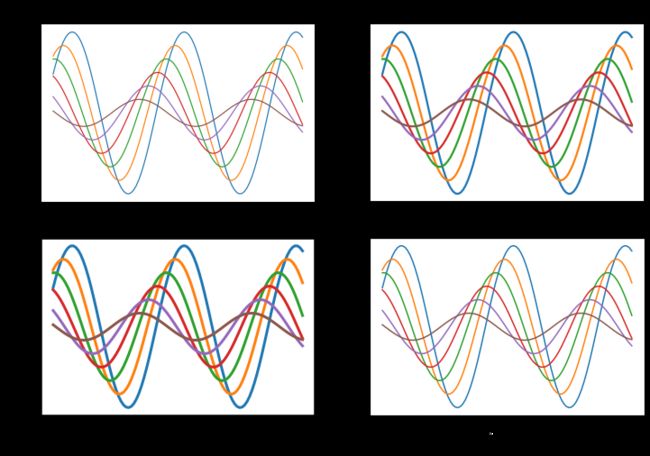
Seaborn一共有4个内置主题，分别为paper、talk、poster和 notebook，对应不同的场合。可使用set_context（）函数设置：

plt.figure(figsize=(12, 8))
sns.set_context('paper')
plt.subplot(221)
sinplot()
plt.title('paper')
sns.set_context('talk')
plt.subplot(222)
sinplot()
plt.title('talk')
sns.set_context('poster')
plt.subplot(223)
sinplot()
plt.title('poster')
sns.set_context('notebook')
plt.subplot(224)
sinplot()
plt.title('notebook')

Output:
Text(0.5, 1.0, ‘notebook’)

Seaborn 的调色板

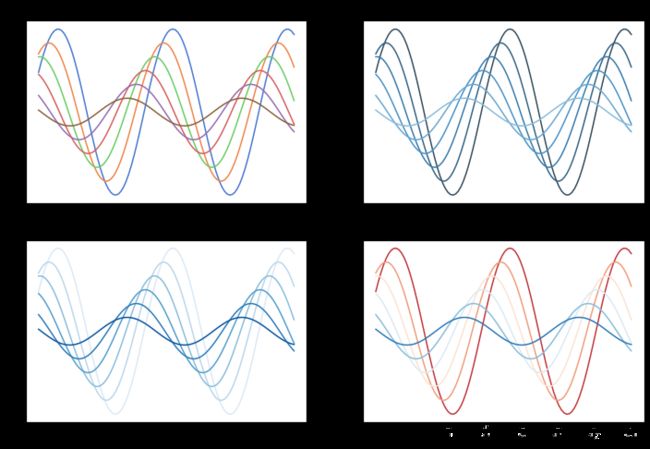
Seaborn拥有极其丰富的调色板库，大致可分为循环、渐变、混合 三类，利用set_palette()函数进行设置：

plt.figure(figsize=(12, 8))
sns.set_palette("muted")
plt.subplot(221)
sinplot()
plt.title('循环')
sns.set_palette("Blues_d")
plt.subplot(222)
sinplot()
plt.title('渐变（深-浅）')
sns.set_palette("Blues")
plt.subplot(223)
sinplot()
plt.title('渐变（浅-深）')
sns.set_palette("RdBu")
plt.subplot(224)
sinplot()
plt.title('混合（红-蓝）')

Output:

Text(0.5, 1.0, '混合（红-蓝）')

Seaborn 分布图

Seaborn 不仅在图形的外观上提供了有效的帮助，还提供了辅助图 形，使我们更快捷地获得可视化结果。先从最简单的正态分布直方图入手：

import numpy.random as npr
size = 1000
rn1 = npr.standard_normal(size)

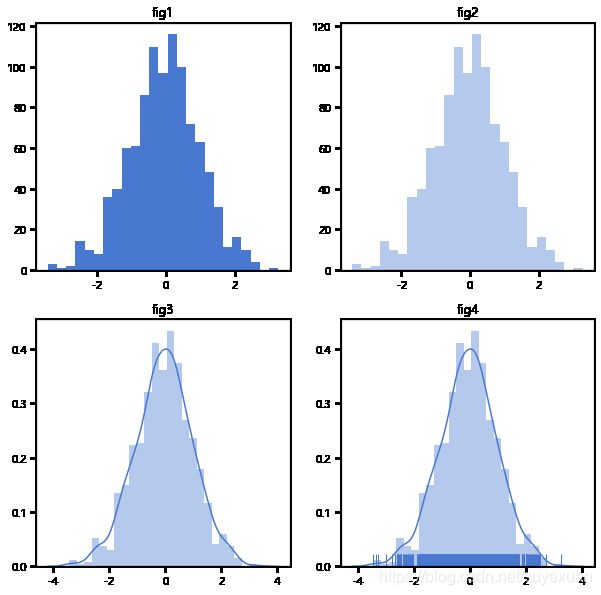
Seaborn中的 distplot 函数起到了类似于 Matplotlib 中的 hist 函数的功 能，但更强大一些。我们通过 kde 及 rug 参数就可以选择是否显示核密度、估计及边际毛毯图：

sns.set_palette("muted")
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(10, 10))
ax1.hist(rn1, bins=25)
ax1.set_title('fig1')
sns.distplot(rn1, bins=25, kde=False, ax=ax2)
ax2.set_title('fig2')
sns.distplot(rn1, bins=25, kde=True, ax=ax3)
ax3.set_title('fig3')
sns.distplot(rn1, bins=25, kde=True, rug=True, ax=ax4)
ax4.set_title('fig4')

Output:

Text(0.5, 1.0, 'fig4')

Scipy 基础教程

SciPy包含致力于解决在科学计算中的常见问题的各个工具箱，它 的不同子模块对应不同的应用，例如插值、积分、优化、图像处理和特 殊函数等。 SciPy可以与其他标准科学计算程序库如 GSL（GNU C 或 C++科学 计算库）或者MATLAB工具箱进行比较，是Python中科学计算程序的核心包，用于有效地计算NumPy矩阵，以便于NumPy和SciPy协同工作。 由于SciPy涉及的领域众多，所以本章只选择部分常用子库进行介绍，并结合实例进行讲解。

回归分析

回归分析（Regression Analysis）是确定两种或两种以上变量之间相 互依赖的定量关系的一种统计分析方法，运用十分广泛。回归分析按照 涉及的变量的多少，可分为一元回归分析和多元回归分析；按照因变量 的多少，可分为简单回归分析和多重回归分析；按照自变量和因变量之 间的关系类型，可分为线性回归分析和非线性回归分析。

回归分析在金融领域的应用十分广泛，比如在 CAPM 模型中 beta 系数的计算，本质上就是一元线性回归，我们先从这个简单的例子入手。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime as dt
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False  #用来正常显示负号

data = pd.read_csv('data.csv', index_col='Date')
data.index = [dt.datetime.strptime(x, '%Y-%m-%d') for x in data.index]
data.head()

	沪深300	中国平安
2015-06-23	0.03214	0.0496
2015-06-24	0.01965	0.0052
2015-06-25	-0.03557	-0.0287
2015-06-26	-0.07868	-0.0605
2015-06-29	-0.03336	-0.0119

data.plot(figsize=(10, 6))
plt.ylabel('涨跌幅')

Output:
Text(0, 0.5, ‘涨跌幅’)

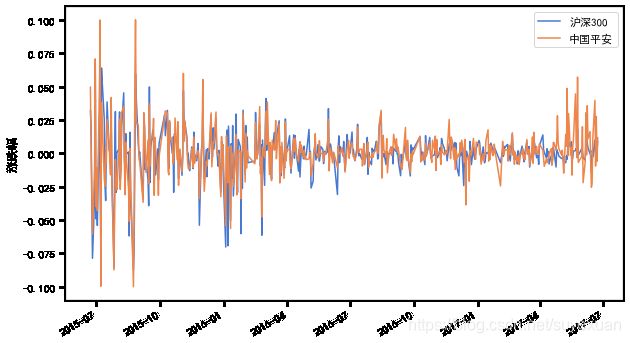
可以发现，中国平安与沪深300的相关性还是比较大的。 接下来要用到StatsModels模块。该模块曾经是scipy.stats下的子模 块，后被重写并成为现在独立的StatsModels模块，在此利用其强大的 OLS（Ordinary Least Square）功能进行回归分析。 首先，引入该模块：

import statsmodels.api as sm
x = data['沪深300'].values
X = sm.add_constant(x)  #添加常数项
y = data['中国平安'].values

接着，对二者的收益率进行线性回归，斜率即beta系数：

model = sm.OLS(y, X)
results = model.fit()
results.params

Output:
array([0.00095063, 0.80946537])

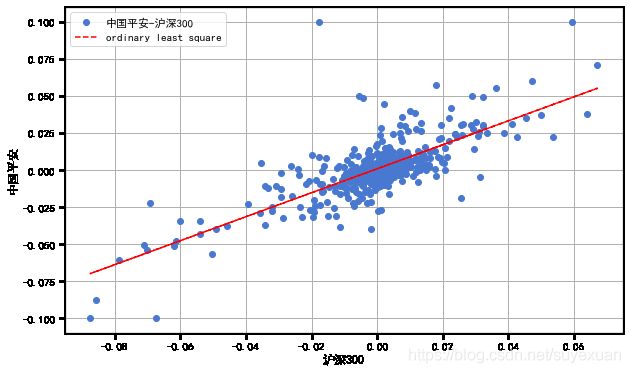
为了让结果更加直观，我们将源数据及拟合直线可视化，如图

plt.figure(figsize=(10, 6))
plt.plot(x, y, 'o', label='中国平安-沪深300')
plt.plot(x, results.fittedvalues, 'r--', label='ordinary least square')
plt.legend()
plt.xlabel('沪深300')
plt.ylabel('中国平安')
plt.grid(True)

同样，归因分析对于投资组合管理十分重要。某一组合的收益与损 失可以被分解为多个表示投资组合权重的因子。我们认为一个虚拟投资组合是由两个随机因子和事先分配的权重构成的，这一分析过程类似于多元线性回归。
接下来分别构造三个随机因子，并对投资组合添加噪声，再对其进 行多元线性回归。与一元线性回归类似，二者仅仅在基函数的数量上有所不同：

factor = npr.rand(1000, 3)
Factor = sm.add_constant(factor)  #添加常数项
fac1 = factor[:, 0]  #因子1
fac2 = factor[:, 1]  #因子2
fac3 = factor[:, 2]  #因子3
e = npr.random(1000)  #噪声
port = fac1 * 0.3 + fac2 * 0.7 + fac3 * 0.4 + e  #虚构投资组合及因子权重

model1 = sm.OLS(port, Factor)
results1 = model1.fit()
results1.params

Output:
array([0.51863602, 0.34964306, 0.63775975, 0.37066742])

可以看到，由于对投资组合添加了一定的噪声，所以导致计算出的 因子权重与原先设置的因子权重相比有了微小的偏差。

插值

插值是在离散数据的基础上补插连续函数，使这条连续曲线通过全 部给定的离散数据点。插值是离散函数逼近的重要方法，可根据函数在
有限个点处的取值状况，估算出函数在其他点处的近似值。
同样，大部分金融数据都是离散数据，所以插值在金融领域的应用 极其广泛，我们先从一个实例入手。
首先，读取近一个月的沪深300指数数据：

data1 = pd.read_csv('data1.csv')
data1.head()

	沪深300
0	3424.1940
1	3424.1669
2	3485.6581
3	3480.4345
4	3492.8845

接下来，导入scipy.interpolate子库对数据进行样条插值：

import scipy.interpolate as spi
X = data1.index  #定义数据点
Y = data1.values  #定义数据点
x = np.arange(0, len(data1), 0.15)  #定义观测点

分别对源数据进行线性及三次样条插值，使用的函数为 splrep 和 splev

ipo1 = spi.splrep(X,Y,k=1) # k 样条拟合顺序（1<=k<=5）
ipo3 = spi.splrep(X,Y,k=3)

iy1 = spi.splev(x,ipo1)
iy3 = spi.splev(x,ipo3)

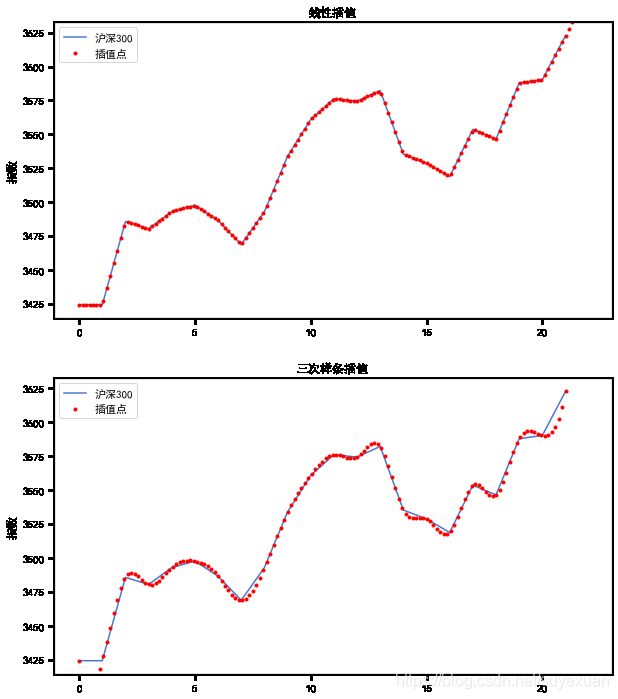
然后，对源数据及插值点进行可视化，效果如图所示

fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10,12))
ax1.plot(X, Y, label='沪深300')
ax1.plot(x, iy1, 'r.', label='插值点')
ax1.set_ylim(Y.min() - 10, Y.max() + 10)
ax1.set_ylabel('指数')
ax1.set_title('线性插值')
ax1.legend()
ax2.plot(X, Y, label='沪深300')
ax2.plot(x, iy3, 'r.', label='插值点')
ax2.set_ylim(Y.min() - 10, Y.max() + 10)
ax2.set_ylabel('指数')
ax2.set_title('三次样条插值')
ax2.legend()

由于源数据本身就是以天为单位的离散数据点，所以在使用线性插值时，插值点与Matplotlib贴合。在使用三次样条插值时，插值点形成 的曲线更为平滑、连续。