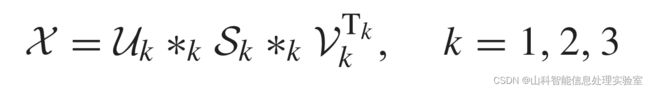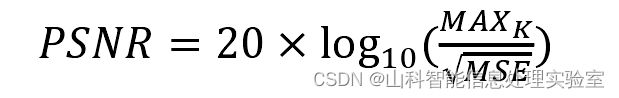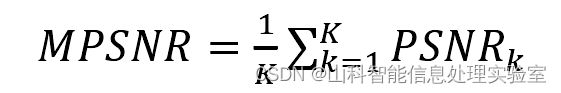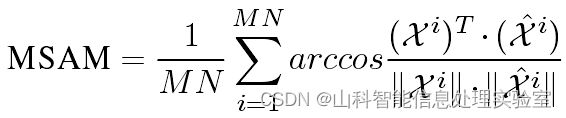基于张量分解的遥感图像恢复及常用高光谱遥感数据集

本文为初期学习总结，本篇文章总结了遥感高光谱图像研究背景、高光谱图像噪声的分类，介绍了基于张量的图像恢复方法及近年来对于张量分解的相关研究，总结了几个常用的图像评价指标，总结了高光谱遥感图像常用的数据集。仍有很多不足，如有错误请指正，本文为方便文献查阅，引用文献将列于被引用章节下方。

目录

一、 高光谱图像及噪声介绍

1.高光谱图像恢复背景

2.噪声分类

（一）云和阴影

（二）条带噪声

（三）高斯噪声

（四）脉冲噪声

二、高光谱图像恢复中张量分解的相关工作

1.CP分解

2.Tucker分解

3.T-SVD：

4.Low-Fibered-Rank Regularization

5.TT分解

6.Tensor Train Rank and Total Variation

7.TR分解

三、图像评价指标

1.PSNR

2.SSIM

3.MSAM

四、常用高光谱遥感的数据集

---

一、 高光谱图像及噪声介绍

1.高光谱图像恢复背景

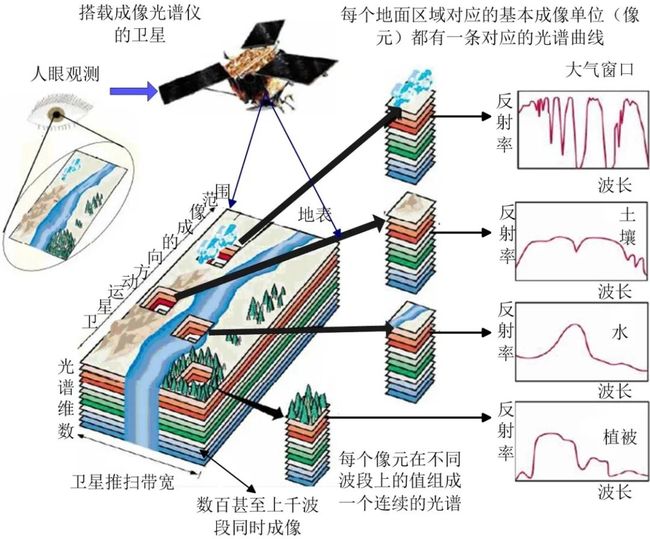
高光谱成像（HSI）在遥感领域快速发展，因为它在军事、地质、环境和农业等领域有着广泛的应用。然而由于成像设备、成像环境以及传输、储存条件等限制，HSI通常会受到种不同类型的噪声的影响，例如高斯噪声、条带噪声、椒盐噪声等，而高光谱图像的噪声往往由两种或多种噪声的混合噪声组成，使得图像不适合进一步的应用。因此，HSI去噪已成为提高后续应用性能的重要预处理步骤，影像信息复原的目标就是从观测的退化影像中反向求解出真实的影像。HSI去噪旨在从其退化观测值估计干净的HSI，这是许多后续应用的关键预处理步骤，核心问题是利用HSI的空间和光谱先验知识。典型的HSI先验包括分段平滑、非局部自相似和低秩。近年来，基于张量分解的去噪方法越来越多的被研究人员所关注，基于张量的分解模型去噪方法是把高光谱图像视作三阶张量数据，而把二维图像去噪算法进行高阶推广，在满足不同张量分解模型的前提下进行去噪，这些方法考虑到了空间域与光谱维之间的联系[1]。

2.噪声分类

（一）云和阴影

成像过程中由于气候原因，目标区域上方天空中频繁出现的云雾,获取到的大部分多时相影像极大可能地在某些时间段上会受到云及云在地面上投射的阴影所造成的污染。此外，影像中云和阴影的干扰情况也会因天气的恶劣程度而受到影响。[2]

图 1-1 不同传感器获取到的影像展示。(a)SPOT-5卫星获取到的云和阴影影像；(b)Hyperion成像仪获取到的条带噪声影像； (c)AVIRIS成像仪获取到的高斯噪声影像；(d)HYDICE成像仪获取到的混合噪声影像

（二）条带噪声

高光谱影像产生条带噪声的主要原因是由成像光谱仪的工作原理、成像仪器及外界成像环境等多种因素所造成的。遥感影像成像仪的核心部件是电荷耦合器件探测元件，在该元件阵列中，存在很多个线状排列的探测元件。自身成像仪器性能的限制或者外界成像环境的影响下，不同探测单元在扫描地物成像的过程中，经常出现对同一辐射能量带来不一致的响应，从而使得收集到的影像受到条带噪声的污染。条带噪声不同于其他噪声，它具有特殊的线性结构和方向性。如图1-1(b)展示了Hyperion高光谱成像仪获取到的高光谱影像中的某个条带波段。

（三）高斯噪声

高斯噪声一般指服从高斯分布的噪声。在高光谱成像的过程中，电荷耦合器件把获取到的电磁波能量转化成图像信息时会带来不同形式的噪声包括暗噪声和读出噪声等。由于这两类噪声频繁地出现在高光谱成像过程中且通常满足高斯分布，因此研究学者将该类噪声定义为高斯噪声，并且假设不同波段上的噪声强弱一致。图1-1(c)展示的是AVIRIS高光谱成像仪获取到的高光谱影像中的某个高斯噪声波段。

（四）脉冲噪声

椒盐噪声也叫做脉冲噪声，表示的是影像中的像素值出现最小值的黑噪点和最大值的白噪点。在高光谱成像过程中，当遭受到大幅度电磁波干扰而导致信号出现急剧变化或者感光片错误的曝光时，就会使得获取到的影像中产生脉冲噪声。如图1-1(d)展示了HYDICE高光谱成像仪获取到的高光谱影像中的某个混合噪声波段。

[1] 宋毅梁. 基于张量分解的高光谱图像去噪算法研究[D]. 四川:四川大学,2021.

[2]陈勇. 遥感影像信息复原问题的张量优化模型及算法研究[D]. 电子科技大学, 2020.

二、高光谱图像恢复中张量分解的相关工作

近年来，研究人员对张量分解模型的去噪算法进行了深入研究，这类算法将高光谱图像利用多维线性张量代数分解模型对高光谱数据进行分析。张量分解有多种类型，如CANDECOMP/PARAFAC（CP）分解、Tucker分解、张量奇异值分解（t-SVD）、张量序列分解（TT）和张量环分解（TR）。

张量分解在高光谱图像中的相关工作

1.CP分解

CP分解将原始张量分解成多个秩1张量的和，秩1张量的最少个数称为CP秩。CP分解是由矩阵秩1分解的和推广而来的，是多个一维向量外积的和，并且分解出的因子具有明显的物理意义。[1]基于CP分解的有效性，研究者将CP分解应用于高光谱影像噪声去除问题[3, 4]，对于一个三阶张量：可分解为

三阶张量的 CP 分解示例图

经典 CP 分解模型去噪算法是基于交替最小二乘的 PARAFAC 算法：

三阶张量的 CP 分解示例图

2.Tucker分解

Tucker分解是将原始张量分解成一个核心张量（core tensor）和多个因子矩阵的形式，其对应的Tucker秩是展开张量的各个维度得到的矩阵的秩组成的向量[1]。由于高维遥感影像在各个维度都具有很强的相关性，因此Tucker分解被广泛地用于遥感影像处理[5, 6]，分解形式：

 三阶张量的 TUCKER 分解示例图

  经典 TUCKER 分解模型的去噪算法为 LRTA 算法：

3.T-SVD：

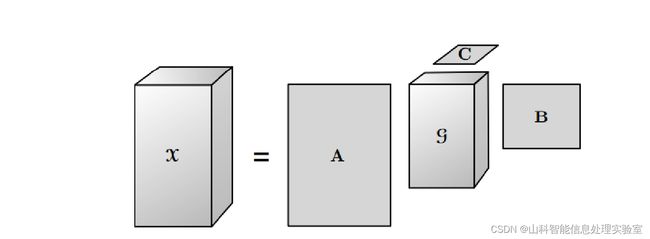
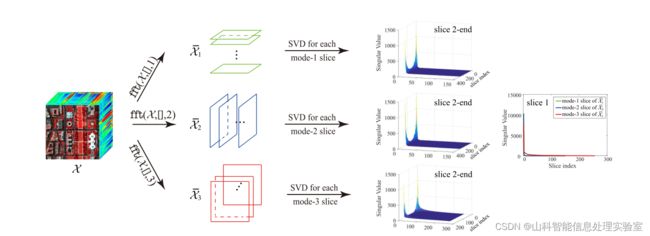
T-SVD是针对三维影像数据的一种矩阵奇异值分解推广，通过张量-张量乘积（t-product）运算将原始张量分解成三个张量的乘积。通过刻画高光谱影像的全局光谱相关性，t-SVD被用于高光谱影像噪声去除问题[7]，对于张量可被分解为：

三阶张量的 T-SVD 分解示例图

4.Low-Fibered-Rank Regularization

Zheng等人[8]将t-SVD发展为mode-k t-SVD，并将HSI建模为相应的低纤维秩分量，进一步将TNN扩展为凸三向TNN和非凸三向对数TNN，并提出了两种混合噪声去除模型。分别引入了3DTNN和3DLogTNN作为其凸松弛和非凸松弛。开发了一种基于ADMM的高效算法，并进行了经验收敛性分析。广泛的实验结果表明，所提方法具有更好地去除混合噪声和更好地保留固有结构的优势。

mode-k t-SVD

 

tensor fibered rank图示

5.TT分解

Bengua等人[9]首先提出了一种基于TT分解的图像修复模型

TMac-TT算法

使用不同的算法恢复90%丢失条目的Peppers图像测试

6.Tensor Train Rank and Total Variation

Ding等人[10]在TT分解中进一步嵌入了总变差（TV）正则化

为了解决TMac-TT借用ket augmentation将低阶张量转换为高阶张量，存在严重的 block-artifacts这个问题，建立了一个基于张量序列（TT）秩和总变差的低秩矩阵分解相结合的优化模型，以保留TT秩的强度并减少block-artifacts。基于TT秩的低秩矩阵分解和TV正则化相结合的LRTC新模型。提出了一种有效的基于BSUM的算法来求解该模型，并保证了收敛性，可以有效地保持张量数据在空间维度上的分段光滑性，并明显减少块伪影。

the isotropic TV公式

BSUM-based algorithm for tensor completion

 

对于不同SR的Lena和Barbara图像不同方法的PSNR、SSIM值和Time值

 

通过不同的方法恢复了一个波段的MSI测试结果。

7.TR分解

Yuan等人[11]和He等人[12]分别提出了一种结合因子正则化和TV正则化的图像修复方法。

Yuan等人提出了一种基于TR分解的高效张量补全算法，该算法在TR潜在空间上使用了低秩约束。

He等人提出的TR完成模型能够利用不同维度的时间序列RS图像的低秩特性。为了进一步探索遥感图像空间信息的平滑性，在TR完成模型中还引入了全变分正则化。使用两种算法，即增广拉格朗日乘子法（ALM）和交替最小二乘法（ALS）有效地求解了该模型。

[3] X. Liu, S. Bourennane, C. Fossati. Denoising of hyperspectral images using the PARAFAC model and statistical performance analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10):3717–3724

[4] X. Guo, X. Huang, L. Zhang, et al. Hyperspectral image noise reduction based on rank-1 tensor decomposition[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 83:50–63

[5] N. Renard, S. Bourennane, J. Blanc-Talon. Denoising and dimensionality reduction using multilinear tools for hyperspectral images[J]. IEEE Geoscience and Remote Sensing Letters, 2008,5(2):138–142

[6] A. Karami, M. Yazdi, A. Z. Asli. Noise reduction of hyperspectral images using kernel nonnegative tucker decomposition[J]. IEEE Journal of Selected Topics in Signal Processing, 2011,5(3):487–493

[7] H. Fan, Y. Chen, Y. Guo, et al. Hyperspectral image restoration using low-rank tensor recovery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2017, 10(10):4589–4604

[8]Zheng Y B, Huang T Z, Zhao X L, et al. Mixed noise removal in hyperspectral image via low-fibered-rank regularization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 58(1): 734-749.

[9] Bengua J A, Phien H N, Tuan H D, et al. Efficient tensor completion for color image and video recovery: Low-rank tensor train[J]. IEEE Transactions on Image Processing, 2017, 26(5): 2466-2479.

[10] Ding M, Huang T Z, Ji T Y, et al. Low-rank tensor completion using matrix factorization based on tensor train rank and total variation[J]. Journal of Scientific Computing, 2019, 81(2): 941-964.

[11] L. Y uan, C. Li, D. Mandic, J. Cao, and Q. Zhao, “Tensor ring decomposition with rank minimization on latent space: An efficient approach for tensor completion,” in Proc. AAAI, 2019, vol. 33, no. 1, pp. 9151–9158.

[12] He W, Yokoya N, Yuan L, et al. Remote sensing image reconstruction using tensor ring completion and total variation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 8998-9009.

三、图像评价指标

目前，对图像去噪效果的判断一般分为主观判断与客观判断。主观判断主要通过对图像的清晰度以及细节信息等进行观察后做出评估。主观判断往往不能反映图像真实还原效果，因此需借助某些客观参数来衡量图像的还原质量。目前较常见的是峰值信噪比（PSNR）[13]与结构相似性（SSIM）[13]。其中峰值信噪比是一种纯客观的评价方式，计算 PSNR之前需要先计算原图像与去噪图像的均方误差（MSE）。光谱角相似度（SAM）[14]也作为评价指标。

1.PSNR

 

 其中MAX是图片可达到的最大像素值，PSNR的值越大说明去噪效果越好。高光谱图像有多个光谱波段，PSNR 只能对某一光谱波段的空间域进行评价

平均峰值信噪比（Mean Peak Signal to Noise Ratio，MPSNR）

2.SSIM

结构相似性（SSIM）是一种能反映人对图像主观观感的评价指标。SSIM 认为图像的像素之间是有关联性的，而这种关联性可以反映图像的结构特征。SSIM 通过比较去噪图像与原图像之间的结构特征来度量去噪算法的还原效果。

 其中x是去噪后的图像，y表示原图像。为对应图像的均值。为对应图像的方差。为了保证 SSIM 在计算时分母不会为 0，引入了常数c1，c2。作为高阶张量数据的高光谱图像，其平均结构相似度（Mean Feature Similarity Index，MSSIM）

3.MSAM

把图像中的每个像元的光谱视为一个高维向量，通过计算两向量间的夹角来度量光谱间的相似性，夹角越小，两光谱越相似。

两个参数分别是复原结果和真实影像的第i个光谱特征。

MPSNR和MSSIM是用来评价空间结构复原的效果，而MSAM是用来说明复原结果光谱信息的保留程度

[13]Z. Wang, A. C. Bovik, H. R. Sheikh, et al. Image quality assessment: From error visibility to
structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4):600–612

[14]R. Yuhas, A. F. H. Goetz, J. W. Boardman. Descrimination among semi-arid landscape end-
members using the Spectral Angle Mapper (SAM) algorithm[C]. Proceeding Summaries 4th
JPL Airborne Earth Science Workshop, Boulder, CO, U.S.A., 1992, 147–149

四、常用高光谱遥感的数据集

引用来源：中科院上海技物所启东光电中心

常用16个高光谱遥感的数据集，包括雄安新区（马蹄湾村）航空高光谱遥感影像分类数据集、Washington DC数据、Urban数据、Pavia University和 Pavia Center数据、Houston数据、Eagle_reize数据、BerlinUrbGrad2009数据、HyRANK数据、Indian Pine数据、Salinas Valley数据、DFC2018 Houston数据、航空高光谱影像 Chikusei、KSC数据集、Cuprite数据、Botswana数据、The River Data Set数据。

数据集：	下载地址：	简介：
雄安新区航空高光谱遥感影像分类数据集	http://www.hrs-cas.com/a/share/shujuchanpin/2019/0501/1049.html雄安马蹄湾村航空高光谱遥感影像数据集_中国科学院遥感与数字地球研究所-高光谱遥感应用技术研究室http://www.hrs-cas.com/a/share/shujuchanpin/2019/0501/1049.html	光谱范围为400-1000 nm，波段数为250个，影像大小为3750*1580。地物类别共计19类
Washington DC	MultiSpec© | Tutorials	数据包含了从 0.4-2.4 µm可见光和近红外波段范围的共191个波段，数据大小为1208*307。
Urban	https://sites.google.com/site/feiyunzhuhomepage/datasets-ground-truths	图像大小为307*307。原始数据有210个波段，在去除噪音和水吸收波段后，一般留下162个波段做后续处理与分析。
Pavia University和 Pavia Center	Hyperspectral Remote Sensing Scenes - Grupo de Inteligencia Computacional (GIC)	传感器一共有115个波段，经过处理后，Pavia University数据有103个波段；Pavia Center 数据有102个波段。两幅影像都有9个地物类别，这两幅影像的类别不完全一致。其中，Pavia University的大小为610*340，Pavia Center的大小是1096*715
Houston	http://www.grss-ieee.org/community/technical-committees/data-fusion/2013-ieee-grss-data-fusion-contest/	数据大小为349*1905，包含光谱范围从364 nm到1046 nm的144个波段。地物覆盖被标注为如下图所示的15个类别。
Eagle_reize	Fusion of LiDAR and Hyperspectral Data	数据大小为2082*1606，包含光谱范围从401 nm到999 nm的252个波段。
BerlinUrbGrad 2009	Berlin-Urban-Gradient dataset 2009 - An EnMAP Preparatory Flight Campaign (Datasets)	真实的HyMap数据包含111个波段，其中空间分辨率为3.6 m的数据大小为6895*1803，空间分辨率为9 m的数据大小为2722*732。
HyRANK	HyRANK Benchmark	五幅图像均有176个光谱波段，图像大小各不相同。所提供的训练样本包含14种地物类别
Indian Pine	Hyperspectral Remote Sensing Scenes - Grupo de Inteligencia Computacional (GIC)	数据大小是145*145，有224个波段，其中有效波段200个。该数据一共有16个农作物类别
Salinas Valley	Hyperspectral Remote Sensing Scenes - Grupo de Inteligencia Computacional (GIC)	数据的空间分辨率是3.7 m，大小是512*217。原始数据有224个波段，去除水汽吸收严重的波段后，还剩下204个波段。该数据包含了16个农作物类别
DFC2018 Houston	2018 IEEE GRSS Data Fusion Challenge – Fusion of Multispectral LiDAR and Hyperspectral Data | Hyperspectral Image Analysis Lab	包含了48个波段的高光谱数据(1 m)，3波段的LiDAR数据(0.5 m)，以及超高分辨率影像(0.05 m)。这个数据包含了20类地物
航空高光谱影像 Chikusei	Naoto YOKOYA	该数据包含了128个波段，范围是343-1018 nm，大小是2517*2335，空间分辨率是2.5 m。共有19类地物，包含城市与农村地区
KSC数据集	Hyperspectral Remote Sensing Scenes - Grupo de Inteligencia Computacional (GIC)	该数据包含了224个波段，水汽噪声波段去除，空间分辨率是18 m，共有13个类别
Cuprite数据	Hyperspectral Remote Sensing Scenes - Grupo de Inteligencia Computacional (GIC)	原始图像有224个波段，波长从370-2480 nm，空间分辨率为20 m
Botswana	Hyperspectral Remote Sensing Scenes - Grupo de Inteligencia Computacional (GIC)	在242个波段获得了30 m像素分辨率的数据，覆盖波段为400-2500 nm并以10 nm为间隔。去除噪声波段后，其余145个波段作为候选特征
The River Data Set	dataset.zip_免费高速下载|百度网盘-分享无限制	其光谱范围为0.4-2.5 μm，光谱分辨率为10 nm，空间分辨率为30 m，共有242个光谱波段。数据集中的影像大小为463*241，去除噪声后有198个波段可用