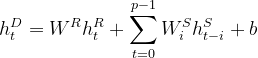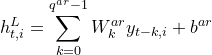《Modeling Long- and Short-Term Temporal Patterns with DeepNeural Networks》学习总结
一、题目
《Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks》
二、研究背景
多元时间序列预测是一个跨领域且重要的机器学习问题。在实际应用中的时态数据往往既具有长期模式也具有短期模式。传统的向量自回归模型无法捕捉多元信号的复杂非线性关系，从而以效率为代价导致性能下降；而高斯过程由于核矩阵的逆运算，在多元时间序列预测上也具有高计算复杂度。
三、创新点
1、针对时态数据中的长短期模式，提出LSTNet模型，通过对多种模型的组合实现对混合、重复时序的分析与预测。
2、针对间隔周期非常长的数据，通过改进GRU提出一种循环跳跃结构，对时序间的相关性进行了捕获。
四、问题分析
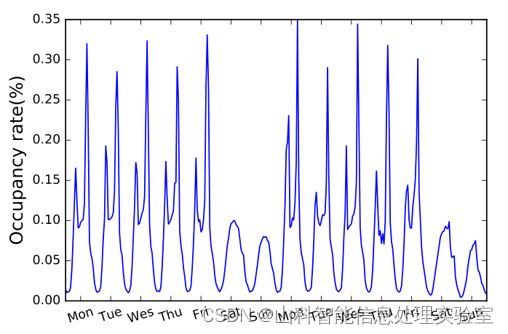
真实数据中，经常出现短期和长期模式混合的情景。下图绘制了高速公路每小时的占用率，以天为单位的周期可反映早晚之间的差异，以周为单位的周期可反映工作日和周末的差异。一个好的时间序列预测模型应该同时捕捉这两种重复出现的模式，从而进行准确的预测。
已知时间序列
，其中
，n是变量的维数，本文的目标是以滚动预测的方式预测一系列未来信号。也就是说，假设已知，预测目标则为
(h是当前时间向前预测的步长)。设时间t时的输入矩阵为
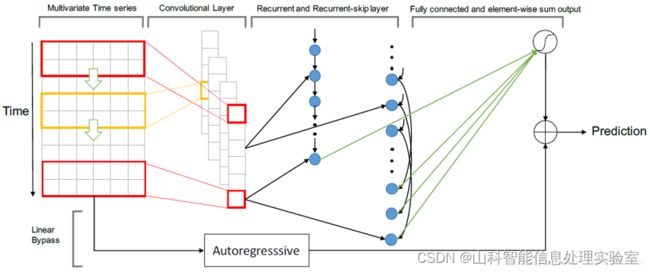
五、模型框架
1、卷积层
LSTNet的第一层是一个没有池化的卷积网络，旨在提取时间维度上的短期模式以及变量之间的局部依赖关系。卷积层由多个滤波器组成，滤波器的宽度为ω，高度为n(高度设置为与变量数量相同)。第k个滤波器扫过输入矩阵X并产生
通过在输入矩阵X的左侧填充零，使每个向量
的长度为T。卷积层的输出矩阵大小为dc×T，其中dc为滤波器个数。
2、循环层
卷积层的输出同时输入到循环层和循环跳跃层。循环层使用门控循环单元（GRU），用以捕获时间序列的时间依赖性以及长期模式。
3、循环-跳跃层
时间序列往往具有周期性规律，循环-跳跃层能够捕捉更长期的信息并充分利用序列的周期特性。具体而言，就是在当前隐藏单元与相邻周期相同时段的隐藏单元建立跳跃链接。
P是跳过的隐藏单元数量。
接下来，使用一个密集层组合循环层和循环-跳跃层的输出。密集层的输入包括时间t时循环层的隐藏状态，记作 
，以及从时间t-p+1至t时循环-跳跃层的p个隐藏状态，记作
；输出的计算公式为
是时间t时神经网络的预测结果。
4、时间注意力层
循环-跳跃层需要一个预定义的超参数p，这对于非季节性的时间序列预测或周期长度随时间变化的预测是不利的。为缓解这一问题，引入注意力机制，它学习输入矩阵每个窗口位置的隐藏表示的加权组合。具体的，在当前时间t时的注意力权重
可以按如下公式计算：
式中
时间注意力层的输出是加权上下文向量
与最后一个窗口的隐藏状态
的拼接，再做一个线性投影运算，得到
![\small h_{t}^{D}=W\left [ c_{t};h_{t-1}^{R} \right ]+b](http://img.e-com-net.com/image/info8/d05f4adee1f54977b7e0ebc768f8387a.gif){kind=small}
5、自回归层
神经网络模型的一个主要缺点是输出的尺度对输入的尺度不敏感。在特定的真实数据集中，输入信号的尺度会以非周期的方式不断变化，这就大大降低了神经网络模型的预测精度。
为了解决这一问题，将LSTNet的最终预测分解为一个线性部分(主要关注局部尺度问题)和一个包含重复模式的非线性部分。在LSTNet体系结构中，采用自回归(AR)模型作为线性分量。设AR层的预测结果为
，AR模型的系数
and
，其中
是输入矩阵上输入窗口的大小。AR模型可以按如下公式表示：
将神经网络部分的输出与AR部分的输出进行求和，得到LSTNet的最终预测结果：
六、实验部分
1、数据集准备
使用四个公开可用的基准数据集，分别为Traffic、Solar-Energy、Electricity、Exchange-Rate。所有数据集按时间顺序分为训练集(60%)、验证集(20%)和测试集(20%)
为了检验时间序列数据中是否存在长期和/或短期重复模式，对四个数据集中随机选择的一些变量绘制了自相关图。
在 (a)，(b)和(c)图中看到，在Traffic, Solar-Energy和Electricity数据集中有高自相关性的重复模式，但在exchange rate数据集中没有。在Traffic与Electricity数据集的曲线图中，可以观察到短期的 (每24小时)和长期的 (每7天)的重复模式；在图(d)中，几乎看不到任何重复的长期模式。
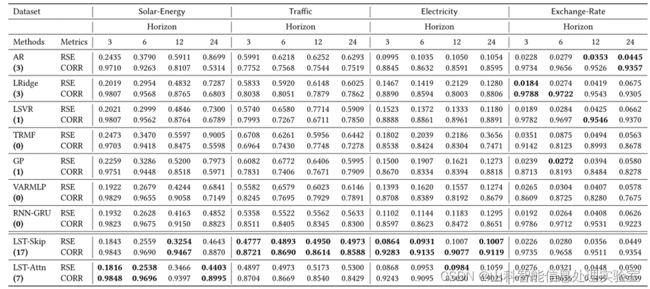
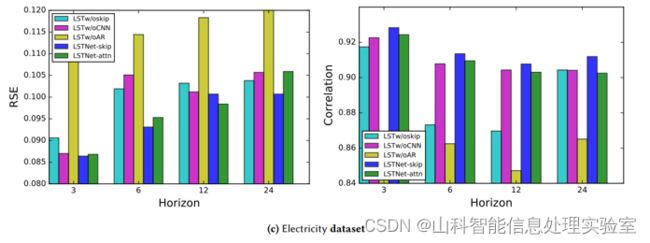
2、评价指标
相对平方误差(RSE)、经验相关系数(CORR)，其中RSE值越小越好，CORR值越大越好。
3、实验结果
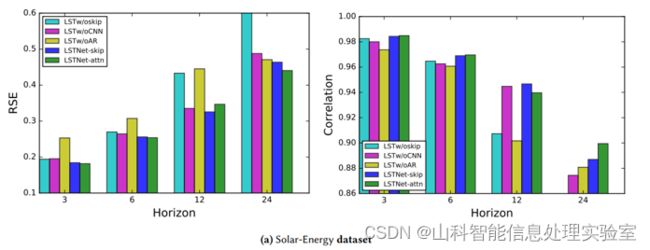
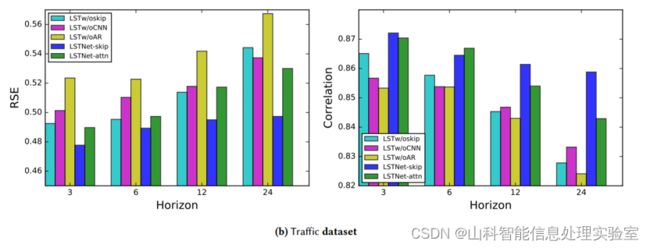
4、消融实验
为证明模型的效率，本文进行了消融研究。具体来说，就是在LSTNet框架中每次删除一部分。模型命名如下：为了说明LSTNet在对时间序列数据中短期和长期重复模式混合建模方面的成功，本文还比较了LSTNet和VAR在Traffic数据集中特定时间序列上的性能。
LSTw/oskip：在LSTNet模型上删除循环-跳跃层和注意力层。
LSTw/oCNN：在LST-skip模型上删除卷积层。
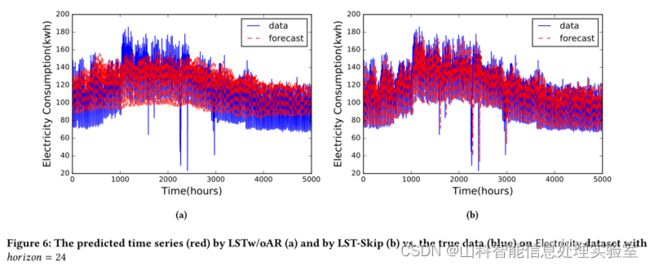
LSTw/oAR：在LST-skip模型上删除自回归层。
5、长/短期混合模式的研究
为了说明LSTNet在对时间序列数据中短期和长期重复模式混合建模方面的成功，本文还比较了LSTNet和VAR在Traffic数据集中特定时间序列上的性能。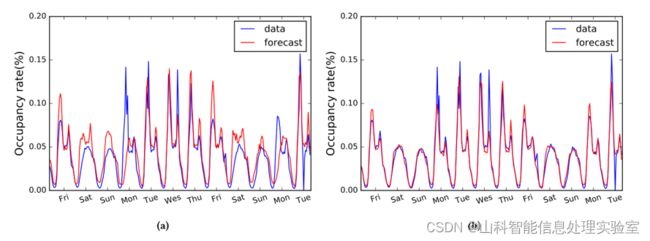
七、总结
本文提出了一种新的深度学习框架(LSTNet)用于多变量时间序列预测。通过结合卷积、循环神经网络以及自回归层的优势，显著改善了多个基准数据集上的时间序列预测的结果；通过深入分析和经验验证，LSTNet模型成功捕捉了数据中的短期和长期重复模式，并结合线性和非线性模型进行了稳健的预测。
八、相关链接
https://paperswithcode.com/paper/modeling-long-and-short-term-temporal
https://arxiv.org/pdf/1703.07015v3.pdf
GitHub - Zhao-zi-jun/multivariate_prediction_master